Thompson Sampling(汤普森采样)

1.power socket problem

一个robot快没电了，Robot 进入了一个包含 5 个不同电源插座的充电室。这些插座中的每一个都会返回略有不同的电荷量，我们希望在最短的时间内让 Baby Robot 充满电，所以我们需要找到最好的插座，然后使用它直到充电完成。

作为介绍，为了让事情更容易处理，让我们简化power socket problem问题。现在，当一个随机变量只有两种可能的结果时，它的行为可以用伯努利分布来描述。用每个socket能充电或不能充电来代替返回会变化数额的电荷。奖励只有两个可能的值：充电时 为1，不充电时为0.当一个随机变量只有两个可能结果时，它的行为可以用伯努利分布来描述。

所以现在，不是每个socket的电荷量不同，而是socket能充电的概率因每个socket而异。我们想找到最大概率能充电的socket，而不是提供最多电荷的socket.

如前所述， Thompson Sampling 生成奖励概率模型. 在这种情况下，得到的奖励是二元的 (win or lose, yes or no, charge or no charge)

beta分布接受两个参数，α(alpha) 和 β (beta). 用最简单的话说这些参数可以分别被认为是成功和失败的计数。

此外, Beta 分布的平均值由下式给出：
[站外图片上传中…(image-40657e-1628079709949)]

最初我们不知道任何给定的socket产生输出的概率是多少，所以我们可以首先将 ‘α’ 和 ‘β’ 都设置为 1，这会产生一条平坦的线 均匀分布（显示为平坦的红色线在图中：
[站外图片上传中…(image-adebf4-1628079709949)]

这种对socket产生输出概率的初始猜测称为 [先验概率]

一旦我们测试了一个socket并获得了奖励，我们就可以修改我们对该socket返回一些电荷的可能性的看法。在收集到一些证据后，这个新概率被称为 [后验概率]

所以，如果一个socket返回一些电荷，奖励将是 1 和 ‘α’, 成功次数的计数, 将增加 1. 失败次数的计数, ‘β’, 将不会增加. 如果没有获得奖励, 那么‘α’将保持不变，‘β’将增加1. 随着收集到的数据越来越多，Beta 分布从一条平坦的线变为越来越准确的平均奖励概率模型. 通过更新 ‘α’ and ‘β’ 的值，汤普森采样算法 is able to describe the estimated mean reward and the level of confidence in this estimate.可以描述估计的均值奖励和这次评估中的置信度.

与 Greedy 算法相反，greedy算法在每个选择时刻选择具有最高估计奖励的动作，即使对该估计的置信度很低，汤普森采样改为从每个动作的 Beta 分布中采样，并选择返回值最高的动作。由于不经常尝试的操作具有广泛的分布，因此它们具有更大范围的可能值 ，如此, 当前估计均值奖励比较低的，但是被选中的次数比那些具有更高估计均值的socket要更少的socket，可返回更大的样本值 并且因此能and therefore become the selected socket at this time step.

在上图中，蓝色曲线的估计平均奖励低于绿色曲线。因此，在贪婪选择下，将选择绿色，而永远不会选择蓝色插槽。相比之下，Thompson Sampling 有效地考虑了曲线的整个宽度，可以看出蓝色socket的曲线延伸到绿色插座的宽度之外。在这种情况下，可以优先选择蓝色socket而不是绿色socket。

随着socket试验次数的增加，对估计均值的置信度也会增加。这反映在概率分布变得更窄，然后采样值将从更接近真实平均值的值范围中提取（参见图 中的绿色曲线）。因此，探索减少而开发利用增加，因为将开始以越来越多的频率开始选择具有更高概率返回奖励的socket。

另一方面，具有低估计平均值的socket将开始被较少地选择，并且倾向于在选择过程中较早地被丢弃。因此，可能永远找不到它们的真实平均值。由于我们只对找到返回奖励概率最高的套接字感兴趣，并尽快找到它，因此我们不关心是否永远无法获得性能不佳的socket的完整信息。

高斯汤普森采样

到目前为止，我们使用的简化socket问题是掌握贝叶斯汤普森采样概念的好方法。但是，要将此方法用于我们的实际socket问题，其中socket不是二进制的，而是返回可变数量的电荷，我们需要稍微更改一下。

在上一个问题中，我们使用 Beta 分布对socket的行为进行建模。之所以选择这一点，是因为简化的socket输出只有两种可能的结果，能充或不能充电，因此可以使用伯努利分布进行描述。当从伯努利分布中得出的值（似然值）乘以从 Beta 分布中得出的值（先验概率）时，结果值（后验概率）也具有 Beta 分布。当发生这种情况时，如似然乘以先验导致后验具有与先验相同的分布类型，则先验称为 [共轭先验]

对于我们的标准socket问题，每个socket返回一个由正态分布描述的真实值。如果我们假设我们知道我们的socket的方差（实际上是 1，因为我们在我们的代码中使用了 numpy randn 函数的未修改版本），那么从维基百科上的共轭先验表中我们可以看到共轭先验也有正态分布。如果我们不知道我们的分布的方差，或者我们正在使用不同的分布，那么我们只需要从表中选择其他共轭先验之一并相应地调整我们的算法。

因此，我们可以使用正态分布对套接字的输出进行建模，并通过更新其均值和方差参数来逐步完善该模型。如果我们不使用方差，而是使用精度 ‘τ’ (tau)，其中精度只是方差的 1（精度 τ = 1/方差），那么我们可以使用均值 ‘μ₀’ 的简单更新规则和总精度 ‘τ₀’ 由下式给出

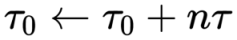
[站外图片上传中…(image-8ecd7e-1628079709949)]

where;

• ‘τ’ 是实际socket输出的精度，在我们的例子中仅为 1。
• ’n’ socket被测试的次数
• ‘xᵢ’ 是在此socket的每个测试“i” 中收到的输出（相当于我们迄今为止使用的奖励“Rᵢ”）。
• ‘μ₀’ 是估计均值（用于对输出建模的分布的均值）。
• ‘τ₀’是用于对输出建模的分布的总精度。

乍一看，这看起来很吓人，但它基本上是说我们有 2 个参数 ‘μ₀’ 和 ‘τ₀’，每次测试socket时都会更新它们，就像我们对 ‘* α*’ 和 ‘β’ 所做的那样。除非在那种情况下，这些参数代表套接字成功和失败的次数而“μ₀”和“τ₀”代表估计均值和精度，代表对估计均值的置信度。 ‘* α*’ 和 ‘β’ 描述的是win or failure 的次数， ‘μ₀’ 和 'τ₀’表示的是估计均值和对估计均值的置信度也就是精度。

此外，我们还可以进行一些其他简化：

• 我们知道从socket返回的电荷量的方差为 1，因此精度 ‘τ’ 也是 1。因此，socket精度的更新就是 τ₀ = τ₀ + n，其中 n 是socket已经过测试的次数，因此每次测试socket时，我们只需将其精度增加 1。

• 对于估计平均值，分子包含scoket产生的所有输出的总和，乘以“τ”。正如我们在第 1 部分的样本平均估计值部分看到的那样，保留奖励总和并不是一个好主意，因为这可能会增长到无法管理的规模。然而，在我们的基础socket实现中，我们总是计算‘Qₜ(a)’，即在时间步‘t’动作‘a’的估计值，它由下式给出：
  [站外图片上传中…(image-90d023-1628079709949)]

• 在这个方程中，“Rᵢ”是在采取动作“a”时在每个时间步获得的奖励，与上面更新方程中使用的术语“xᵢ”相同。因此，我们可以简单地用‘nQₜ(a)’替换更新方程中的求和，最终得到以下简化的更新方程：
  [站外图片上传中…(image-3a094e-1628079709949)]

通过这些简化，我们驯服了可怕的数学！现在很明显，我们需要做的就是保持对每个socket奖励的均值和精度的估计，然后使用 2 个简单的规则来更新这些值。当这些方程被翻译成代码时，事情变得更加清晰。