[JSOI2009] 等差数列（线段树）

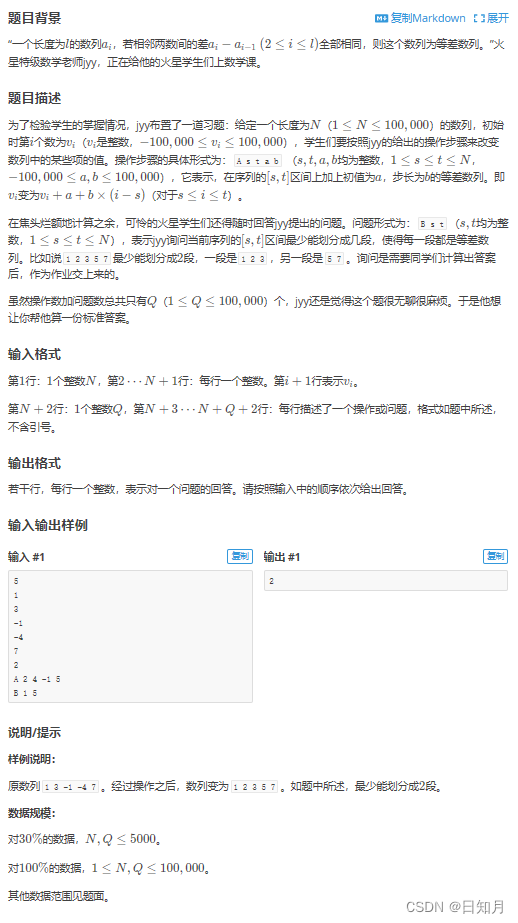
题目来源：洛谷P4243

首先发现有区间赋值和区间查询操作，考虑线段树。发现 $A$ 操作加的都是一个等差数列，直接在原序列上操作并不好维护，考虑换成差分序列，设 $add(l,r,x)$ 表示在区间 $[l,r]$ 都加上 $x$ ，对于 $Astab$，转变为三步：
$1.add(s,s,a)2.add(s+1,t,b)(if(s+1\le t))3.add(t+1,t+1,-(a+b\ast (t-s)))$
然后考虑我们在线段树上应该维护什么，观察 $B$ 操作，我们直观的想相等的一段一定是一段等差数列，直接维护相等段即可。但这显然小瞧这道题了，观察下面的 $hack$ 数据：

$2333$(差分序列)

按照我们刚才的思路，这段差分序列构成的是两端等差数列，但是 1 3 6 9 12 中的 3 6 9 12 显然是一段等差数列，对于 $3$ 的差分数组维护的是 $3$ 与 $1$ 之间的信息，与 3 6 9 12 组成的等差数列并无直接关系。换而言之，对于一段连续的相等段，在前面加上一个不相等的数（后文简称作散数）我们也认为他是一段。

那这怎么维护呢？感觉好难维护，换思路吗？
确实得换思路，但还是线段树维护差分，只不过我们不要直接去维护这个东西，我们仍旧考虑维护连续段，把散数的情况在转移过程中，直接解决掉。

我们设 $s[0\setminus 1\setminus 2\setminus 3]$ 表示 左右端点都不含\左端点含，右端点不含\左端点不含，右端点含\左右端点都含 的区间等差数列最少的个数。
四个转移方程式类似，我们以 $s[0]$ 为例，设左区间为 $l$ ，右区间为 $r$ ，合并区间为 $x$ ，区间左端点为 $lnum$ ，右端点为 $rnum$，则有转移方程式：
$x.s[0]=min(l.s[2]+r.s[1]-[l.rnum==r.lnum],l.s[0]+r.s[1],l.s[2]+r.s[0])$
第一个表示，两个都贴如果中间两数相等，说明中间的等差数列可以合并，总数减一，否则直接相加。
第二个表示，左不贴右贴，左区间不包含的那个右端点就会被右区间的直接合并（当成散数来处理）。
第三个与第二个类似。
为什么没有 $l.s[0]+r.s[0]$ ？ 因为如果两边都不贴，那么中间就会产生两个散数，而右端只能处理一个散数，所以此转移不成立。

为什么要这样设状态：因为我们要处理的状态是 散数+连续段 ，而散数只有一个，连续块很好维护，我们可以考虑抛弃散数维护，在合并时顺便处理散块，这样就变得容易维护状态。

对于 $A$ 操作，我们只需要更改 $lnum,rnum$ 即可，因为整体加对于等差数列的数量没有影响，懒标记同样只需要维护 $lnum,rnum$ 。
对于 $B$ 操作，因为左端点可以直接当成散数处理，所以我们只需要查询 $[l+1,r]$ 的 $s[3]$ 即可。（注意特判 $l=r$ 的情况）

#include<bits/stdc++.h>
using namespace std;
int n,v[100010],a[100010],q,s,t,A,B;
char lx;
struct scc
{
	int s[4],lnum,rnum;
	scc operator + (const scc &x) const
	{
		scc y;
		y.lnum=lnum;
		y.rnum=x.rnum;
		y.s[0]=min(s[2]+x.s[1]-(rnum==x.lnum),min(s[2]+x.s[0],s[0]+x.s[1]));
		y.s[1]=min(s[3]+x.s[1]-(rnum==x.lnum),min(s[1]+x.s[1],s[3]+x.s[0]));
		y.s[2]=min(s[2]+x.s[3]-(rnum==x.lnum),min(s[2]+x.s[2],s[0]+x.s[3]));
		y.s[3]=min(s[3]+x.s[3]-(rnum==x.lnum),min(s[1]+x.s[3],s[3]+x.s[2]));
		return y;
	}
};
struct node
{
	int l,r,add;
	scc num;
} tree[400000];
void build(int p,int l,int r)
{
	tree[p].l=l;
	tree[p].r=r;
	if(l==r)
	{
		tree[p].num.lnum=a[l];
		tree[p].num.rnum=a[r];
		tree[p].num.s[1]=1;
		tree[p].num.s[2]=1;
		tree[p].num.s[3]=1;
		return;
	}
	int mid=(l+r)/2;
	build(2*p,l,mid);
	build(2*p+1,mid+1,r);
	tree[p].num=tree[2*p].num+tree[2*p+1].num;
}
void spread(int p)
{
	if(tree[p].add)
	{
		tree[2*p].add+=tree[p].add;
		tree[2*p].num.lnum+=tree[p].add;
		tree[2*p].num.rnum+=tree[p].add;
		tree[2*p+1].add+=tree[p].add;
		tree[2*p+1].num.lnum+=tree[p].add;
		tree[2*p+1].num.rnum+=tree[p].add;
		tree[p].add=0;
	}
}
void change(int p,int l,int r,int x)
{
	if(tree[p].l>=l&&tree[p].r<=r)
	{
		tree[p].add+=x;
		tree[p].num.lnum+=x;
		tree[p].num.rnum+=x;
		return;
	}
	spread(p);
	int mid=(tree[p].l+tree[p].r)/2;
	if(l<=mid)
	change(2*p,l,r,x);
	if(r>mid)
	change(2*p+1,l,r,x);
	tree[p].num=tree[2*p].num+tree[2*p+1].num;
}
node ask(int p,int l,int r)
{
	if(tree[p].l>=l&&tree[p].r<=r)
	return tree[p];
	spread(p);
	int mid=(tree[p].l+tree[p].r)/2;
	if(l<=mid&&r<=mid)
	return ask(2*p,l,r);
	if(l>mid&&r>mid)
	return ask(2*p+1,l,r);
	node x=ask(2*p,l,r),y=ask(2*p+1,l,r),z;
	z.num=x.num+y.num;
	return z;
}
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	scanf("%d",&v[i]);
	for(int i=2;i<=n;i++)
	a[i]=v[i]-v[i-1];
	if(n==1)
	{
		scanf("%d",&q);
		while(q--)
		{
			scanf("\n%c%d%d",&lx,&s,&t);
			if(lx=='A')
			scanf("%d%d",&A,&B);
			else
			puts("1");
		}
		return 0;
	}
	build(1,2,n);
	scanf("%d",&q);
	while(q--)
	{
		scanf("\n%c%d%d",&lx,&s,&t);
		if(lx=='A')
		{
			scanf("%d%d",&A,&B);
			if(s!=1)
			change(1,s,s,A);
			if(s+1<=t)
			change(1,s+1,t,B);
			if(t+1<=n)
			change(1,t+1,t+1,-(A+B*(t-s)));
		}
		else
		{
			if(s==t)
			puts("1");
			else
			printf("%d\n",ask(1,s+1,t).num.s[3]);
		}
	}
	return 0;
}

总结：对于线段树一个状态不好处理时，考虑分开不好处理的部分，在合并时去处理。