（python）动态规划

前言

        曾经有一位叫做小明的年轻人，他生活在一个被困在连绵不断的山脉中的村庄里。这座村庄每年都会受到洪水的威胁，而村民们只能通过一条崎岖而危险的小路逃离洪水的侵袭。小明决定解决这个问题。他花了很长时间研究了地形图和洪水的模式，最终他发现了一种方法：他可以在山脚下建造一条巨大的堤坝，当洪水来临时，它将会拦截洪水并将其引导到一个安全的区域。但是，建造堤坝需要花费大量的金钱和人力，而小明的村庄资源有限。于是，他开始思考如何以最少的成本建造堤坝。

        小明意识到这其实是一个动态规划的问题。他将整个过程分解成了一系列子问题：在每一段路上，他都需要决定是否要在当前位置建造堤坝。而为了做出最优的决策，他需要考虑之前每一段路上建造堤坝的状态，以及当前路段的地形和洪水情况。

        通过动态规划，小明最终找到了一种最优的建坝方案：在每一段路上，他根据之前的决策和当前的条件，计算出建造堤坝和不建造堤坝的成本，然后选择成本更低的方案。最终，他成功地建造了一座经济高效且能有效防止洪水的堤坝，使村庄免受洪水的威胁。

        这个故事告诉我们，动态规划不仅可以解决实际生活中的问题，而且可以帮助我们找到最优的解决方案，以最小的成本达成我们的目标。

目录

应用领域

算法的显著特征

一般步骤 

优点 

动态规划算法的模板样例 

实战

问题

(1)朴素递归算法

(2)记忆化搜索

(3)动态规划

(4)动态规划2

注意

总结 

---

应用领域

        动态规划广泛应用于各个领域，包括计算机视觉、自然语言处理、生物信息学、经济学等，常见的应用包括图像处理、文本处理、序列比对等。

        动态规划通常用于求解最优化问题，例如最长递增子序列、最大子数组和、最短路径等。这些问题通常具有重叠子问题和最优子结构性质。

算法的显著特征

        

1. 最优子结构 问题的最优解可以通过子问题的最优解来构建。这意味着问题可以分解成相互重叠的子问题，并且子问题之间存在递归的关系。
2. 重叠子问题 在动态规划中，同一个子问题可能会被多次求解。为了避免重复计算，可以使用记忆化搜索或者自底向上的迭代方法来存储子问题的解。
3. 状态转移方程 动态规划通过定义状态和状态之间的转移关系来描述问题。通过找到状态之间的转移规律，可以建立状态转移方程，从而求解问题。
4. 自底向上或自顶向下 动态规划可以采用自底向上的迭代方法或者自顶向下的递归方法来求解问题。自底向上的方法从最小的子问题开始，逐步求解更大规模的问题；而自顶向下的方法则从整体问题开始，通过递归地解决子问题来求解整个问题。
5. 空间优化 动态规划通常可以通过状态压缩或者滚动数组等方法来进行空间优化，减少空间复杂度。

一般步骤 

1. 定义状态 明确定义问题的状态，通常使用一个或多个变量来表示状态。
2. 初始化 初始化状态的初始值，通常包括边界状态或者初始条件。
3. 状态转移方程 根据问题的最优子结构性质，定义状态之间的转移关系，建立状态转移方程。
4. 递推求解 根据状态转移方程，通过迭代或递归的方式求解问题，并存储子问题的解以避免重复计算。
5. 返回结果 根据问题的要求，返回最终的结果。

优点 

        总的来说，动态规划算法是一种强大的问题求解方法，具有较高的效率和灵活性，在算法设计和实现中具有重要的地位和应用价值。

1. 高效性：动态规划算法通过存储子问题的解来避免重复计算，从而大大减少了问题的时间复杂度，提高了算法的效率。

2. 简单易懂：动态规划算法的思想相对直观，基于问题的最优子结构性质，可以较为容易地建立状态转移方程，从而解决问题。

3. 适用性广泛：动态规划算法适用于多种问题，包括但不限于最优化问题、搜索问题、计数问题等，可以灵活应用于不同领域的算法设计中。

4. 可解决复杂问题：动态规划算法通常能够解决一些具有较高复杂度的问题，如旅行商问题、背包问题等，通过合理的状态定义和状态转移方程，可以有效求解这些问题。

5. 可优化性：动态规划算法在求解过程中，可以通过优化空间复杂度、状态压缩等方式进一步提高算法的效率，使得算法更加灵活和可扩展。

动态规划算法的模板样例 

用python写一个算法模板,基本上可以套用.

def dynamic_programming_template():
    # Step 1: Define states
    # 定义状态
    dp = [0] * n  # 初始化状态数组，n为问题规模
    
    # Step 2: Initialization
    # 初始化
    dp[0] = initial_value
    
    # Step 3: State transition
    # 状态转移方程
    for i in range(1, n):
        dp[i] = calculate(dp[i-1], ...)
        # 或者通过状态转移方程递推求解
        # dp[i] = max/min(dp[i-1], ...)
    
    # Step 4: Return the result
    # 返回结果
    return dp[n-1]  # 或者根据问题要求返回特定的状态值

实战

问题

斐波那契数列是一个满足递归又可以拆解成各个子问题的数列问题.

        fib(x)={ 1   x=1,2
                    fib(x−1)+fib(x−2)  x>2} 

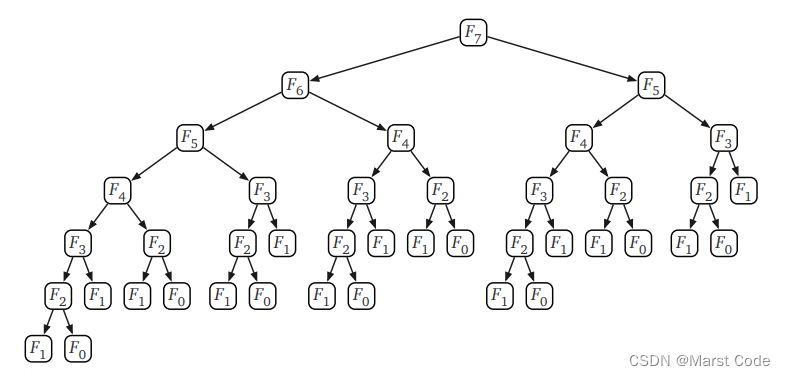
(1)朴素递归算法

时间复杂度 O(2的n次方)
            在每个递归调用中，都需要进行两次递归调用，因此递归树的高度为 n，每层的节点数量大约是    前一层节点数量的两倍

空间复杂度 O(n)
            在递归调用的过程中，系统需要维护一个递归调用栈，其大小与递归树的深度相对应，因此空间复杂度与时间复杂度相似，也是指数级别增长。

class Solution:

    def Fibonacci_base(self, n: int) -> int:
        """
        现在要求输入一个正整数 n ，请你输出斐波那契数列的第 n 项
        斐波那契数列是一个满足
        fib(x)={ 1   x=1,2
        fib(x−1)+fib(x−2)  x>2
        时间复杂度 O(2的n次方)
            在每个递归调用中，都需要进行两次递归调用，因此递归树的高度为 n，每层的节点数量大约是    前一层节点数量的两倍
        空间复杂度 O(n)
            在递归调用的过程中，系统需要维护一个递归调用栈，其大小与递归树的深度相对应，
            因此空间复杂度与时间复杂度相似，也是指数级别增长。
        :param n:
        :return:
        """
        if n == 1 or n == 2:
            return 1

        if n > 2:
            res = self.Fibonacci_base(n - 1) + self.Fibonacci_base(n - 2)
            return res

(2)记忆化搜索

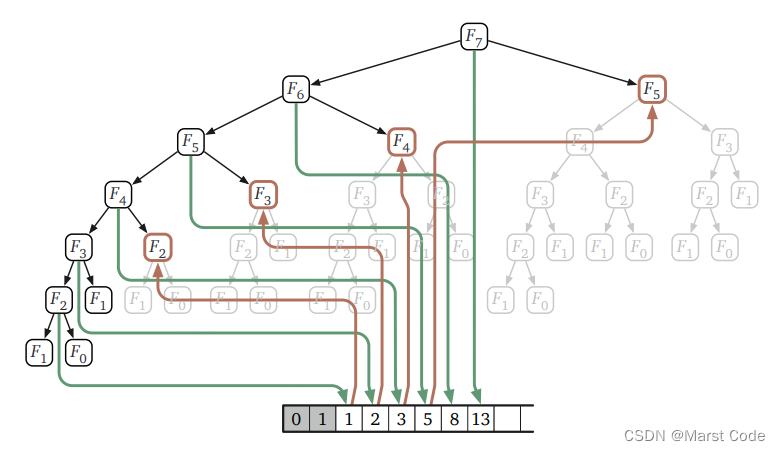
在前面(1)的基础上,发现有大量的重复计算,可以通过记忆的方式避免.

优化 通过记录递归调用的结果并在需要时再次查找，我们可以大大加快递归算法的速度。(指数级别的提升)

在python语言里,可以用字典来存储计算过的结果.

（注:字典是一种基于哈希表实现的数据结构，具有高效的查询性能。字典的查询操作的平均时间复杂度为 O(1)，即使在最坏情况下（哈希冲突较多），时间复杂度也是 O(n)，其中 n 是字典中键值对的数量。）

时间复杂度是 O(n)  
        每个斐波那契数只计算一次
空间复杂度是 O(n) 
        递归调用的最大深度是 n

class Solution:
    count = 0
    cache = {1: 1, 2: 1}


    def Fibonacci(self, n: int) -> int:
        """
        现在要求输入一个正整数 n ，请你输出斐波那契数列的第 n 项
        斐波那契数列是一个满足
        fib(x)={ 1   x=1,2
        fib(x−1)+fib(x−2)  x>2
        时间复杂度是 O(n)  每个斐波那契数只计算一次
        空间复杂度是 O(n) 递归调用的最大深度是 n
        :param n:
        :return:
        """
        self.count += 1
        if n in self.cache.keys():
            return self.cache[n]

        if n > 2:
            res = self.Fibonacci(n - 1) + self.Fibonacci(n - 2)
            if isinstance(res, int):
                self.cache[n] = res
            return res

(3)动态规划

优化 在（2）的基础上,进一步减少了函数的调用(指数级别的提升)

时间复杂度是 O(n) 
    每次迭代都只涉及常数次的操作
空间复杂度是 O(n) 
    数组的长度为 n+1

 

class Solution:

    @staticmethod
    def Fibonacci_array(n: int) -> int:
        """
        现在要求输入一个正整数 n ，请你输出斐波那契数列的第 n 项
        斐波那契数列是一个满足
        fib(x)={ 1   x=1,2
        fib(x−1)+fib(x−2)  x>2

        时间复杂度是 O(n) 每次迭代都只涉及常数次的操作
        空间复杂度是 O(n) 数组的长度为 n+1
        :param n:
        :return:
        """
        dp = {}  # 初始化状态数组，n为问题规模
        # Step 2: Initialization
        # 初始化
        dp[0] = 1
        dp[1] = 1
        # Step 3: State transition
        # 状态转移方程
        for i in range(2, n):
            dp[i] = dp[i - 1] + dp[i - 2]
        # Step 4: Return the result
        # 返回结果
        # print(dp[n - 1])
        return dp[n - 1]  # 或者根据问题要求返回特定的状态值

(4)动态规划2

在许多动态规划算法中，并不需要保留所有中间结果直到计算结束.

优化 在(3)的基础上,只需要2个元素去记忆最后2次的运算结果.(节省运算的空间)

时间复杂度是 O(n)  
    迭代次数与 n 相关
空间复杂度是 O(1)  
    只需存储两个变量

class Solution:

    @staticmethod
    def Fibonacci_temp(n: int) -> int:
        """
        现在要求输入一个正整数 n ，请你输出斐波那契数列的第 n 项
        斐波那契数列是一个满足
        fib(x)={ 1   x=1,2
        fib(x−1)+fib(x−2)  x>2
        时间复杂度是 O(n)  迭代次数与 n 相关
        空间复杂度是 O(1)  只需存储两个变量
        :param n:
        :return:
        """

        # Step 2: Initialization
        # 初始化
        if n == 1 or n == 2:
            return 1
        # 前一个
        prev = 1
        # 当前
        curr = 1
        # Step 3: State transition
        # 状态转移方程
        for i in range(2, n):
            next = prev + curr
            prev = curr
            curr = next
        # Step 4: Return the result
        # 返回结果
        print(curr)
        return curr

注意

1. 定义子问题和状态： 在应用动态规划时，首先要定义清楚原始问题的子问题和问题的状态。子问题是原始问题的一部分，状态则是描述子问题的具体变量。确保子问题之间是相互独立且有重叠性的，这样才能有效利用动态规划的优势。

2. 状态转移方程： 对于每个子问题，需要找到状态之间的转移关系或递推关系。这个关系描述了如何从一个状态转移到下一个状态，通常通过状态转移方程来表示。这是动态规划问题中最核心的部分。

3. 初始化： 动态规划通常需要初始化一个或多个状态作为基础，这些状态是递推关系的起点。确保初始化的状态是符合问题要求的，并能够正确启动递推过程。

4. 计算顺序： 确定动态规划问题的计算顺序。通常采用自底向上的方法，先计算较小规模的子问题，然后逐步扩展到更大规模的问题，直到解决原始问题。也可以采用递归加记忆化的方法，从顶部向下解决问题，确保避免重复计算。

5. 空间优化： 在实际应用中，可以针对状态转移过程进行空间优化，避免使用过多的额外空间。有时可以只保留必要的状态，而不需要全部保存中间过程的状态。

6. 边界条件： 确保考虑到问题的边界条件，例如数组或字符串的边界情况，在状态转移过程中需要特别处理以避免越界或错误结果。

7. 问题建模： 动态规划要求将原始问题清晰地抽象成数学模型，包括定义状态、确定状态转移方程、初始化条件等。正确的问题建模是解决动态规划问题的关键。

8. 复杂度分析： 最后，要分析动态规划算法的时间复杂度和空间复杂度。合理的动态规划算法应该在可接受的时间和空间复杂度内解决问题。

总结 

        动态规划是一种强大的问题求解方法，在解决具有重叠子问题和最优子结构性质的问题时，能够提供高效且正确的解决方案。