分治算法主定理
在学习分治的时候,通常都会遇到通用分治算法递推式:
其中 T(n)代表了分治算法的时间复杂度,n代表了问题的输入规模,a和b分别代表n个输入实例划分为b个子问题,其中a个需要被处理;最后f(n)代表最后合并处理后的结果所需要的时间复杂度。显而易见,T(n)的增长次数取决于a,b已经f(n)。通常会直接给出如下的主定理来描述T(n):
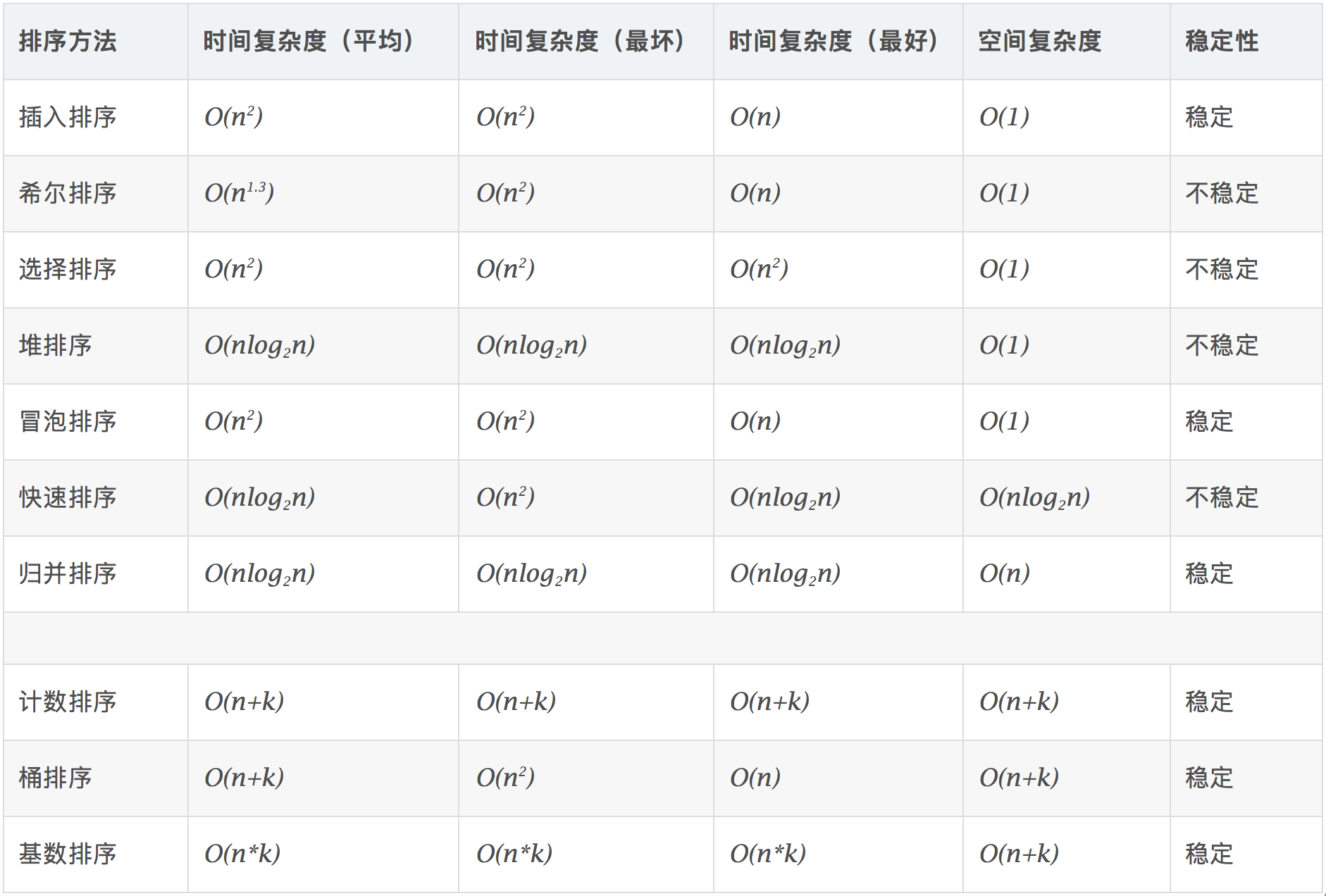
一、排序
归并排序
归并模板
归并属于分治算法,有三个步骤
void merge_sort(int q[], int l, int r)
{
//递归的终止情况
if(l >= r) return;
//第一步:分成子问题
int mid = l + r >> 1;
//第二步:递归处理子问题
merge_sort(q, l, mid ), merge_sort(q, mid + 1, r);
//第三步:合并子问题
int k = 0, i = l, j = mid + 1, tmp[r - l + 1];
while(i <= mid && j <= r)
if(q[i] <= q[j]) tmp[k++] = q[i++];
else tmp[k++] = q[j++];
while(i <= mid) tmp[k++] = q[i++];
while(j <= r) tmp[k++] = q[j++];
for(k = 0, i = l; i <= r; k++, i++) q[i] = tmp[k];
}归并排序属于分治法, 很容易写出递归式:
T(n)=2T(n/2)+f(n)T(n)=2T(n/2)+f(n)
其中, 2T(n/2)2T(n/2) 是子问题的时间复杂度, f(n)f(n) 是合并子问题的时间复杂度
快速排序
相当于双指针从数组两端找数,当量指针都不符合循环条件时,对该位置的数进行交换。
void quick_sort(int q[], int l, int r)
{
//递归的终止情况
if(l >= r) return;
//第一步:分成子问题
int i = l - 1, j = r + 1, x = q[l + r >> 1];
while(i < j)
{
do i++; while(q[i] < x);
do j--; while(q[j] > x);
if(i < j) swap(q[i], q[j]);
}
//第二步:递归处理子问题
quick_sort(q, l, j), quick_sort(q, j + 1, r);
//第三步:子问题合并.快排这一步不需要操作,但归并排序的核心在这一步骤
}
二、二分查找
给定一个按照升序排列的长度为n的整数数组,以及 q 个查询。
对于每个查询,返回一个元素k的起始位置和终止位置(位置从0开始计数)。
如果数组中不存在该元素,则返回“-1 -1”。
#include <iostream>
using namespace std;
const int maxn = 100005;
int n, q, x, a[maxn];
int main() {
scanf("%d%d", &n, &q);
for (int i = 0; i < n; i++) scanf("%d", &a[i]);
while (q--) {
scanf("%d", &x);
int l = 0, r = n - 1;
while (l < r) {
int mid = l + r >> 1;
if (a[mid] < x) l = mid + 1;
else r = mid;
}
if (a[l] != x) {
printf("-1 -1\n");
continue;
}
int l1 = l, r1 = n;
while (l1 + 1 < r1) {
int mid = l1 + r1 >> 1;
if (a[mid] <= x) l1 = mid;
else r1 = mid;
}
printf("%d %d\n", l, l1);
}
return 0;
}
可用二分查找的问题:
可以先写一个check函数
判定在check的情况下(true和false的情况下),如何更新区间。
在check(m)==true的分支下是:
l=mid的情况,中间点的更新方式是m=(l+r+1)/2
r=mid的情况,中间点的更新方式是m=(l+r)/2
这种方法保证了:
1. 最后的l==r
2. 搜索到达的答案是闭区间的,即a[l]是满足check()条件的。
三、线性时间选择
步骤:
(1)将n个输入元素划分成n/5(向上取整)个组,每组5个元素,最多只可能有一个组不是5个元素。用任意一种排序算法,将每组中的元素排好序,并取出每组的中位数,共n/5(向上取整)个。
(2)递归调用select来找出这n/5(向上取整)个元素的中位数。如果n/5(向上取整)是偶数,就找它的2个中位数中较大的一个。以这个元素作为划分基准。
#include <bits/stdc++.h>
using namespace std;
void bubbleSort(int a[],int p,int r)
{
for(int i=p; i<r; i++)
{
for(int j=i+1; j<=r; j++)
{
if(a[j]<a[i])swap(a[i],a[j]);
}
}
}
int Partition(int a[],int p,int r,int val)
{
int pos;
for(int q=p; q<=r; q++)
{
if(a[q]==val)
{
pos=q;
break;
}
}
swap(a[p],a[pos]);
int i=p,j=r+1,x=a[p];
while(1)
{
while(a[++i]<x&&i<r);
while(a[--j]>x);
if(i>=j)break;
swap(a[i],a[j]);
}
a[p]=a[j];
a[j]=x;
return j;
}
int Select(int a[],int p,int r,int k)
{
if(r-p<75)
{
bubbleSort(a,p,r);
return a[p+k-1];
}
//找中位数的中位数,r-p-4即上面所说的n-5
for(int i=0; i<=(r-p-4)/5; i++) //把每个组的中位数交换到区间[p,p+(r-p-4)/4]
{
int s=p+5*i,t=s+4;
for(int j=0; j<3; j++) //冒泡排序,从后开始排,结果使得后三个数是排好顺序的(递增)
{
for(int n=s; n<t-j; n++)
{
if(a[n]>a[n+1])swap(a[n],a[n-1]);
}
}
swap(a[p+i],a[s+2]);//交换每组中的中位数到前面
}
//(r-p-4)/5表示组数-1,则[p,p+(r-p-4)/5]的区间长度等于组数
int x=Select(a,p,p+(r-p-4)/5,(r-p+1)/10);//求中位数的中位数
/*
(r-p+1)/10 = (p+(r+p-4)/5-p+1)/2
*/
int i=Partition(a,p,r,x),j=i-p+1;
if(k<=j)return Select(a,p,i,k);
else return Select(a,i+1,r,k-j);
}
int main()
{
int x;
//数组a存了0-79
int a[80]= {3,1,7,6,5,9,8,2,0,4,13,11,17,16,15,19,18,12,10,14,23,21,27,26,25,29,28,22,20,24,33,31,37,36,35,39,38,32,30,34,43,41,47,46,45,49,48,42,40,44,53,51,57,56,55,59,58,52,50,54,63,61,67,66,65,69,68,62,60,64,73,71,77,76,75,79,78,72,70,74,
};
cin>>x;
printf("第%d大的数是%d\n",x,Select(a,0,79,x));
}
时间复杂度
T(n)= Tn/57) + T(7n/10+6)+ O(n) n>=4
T(n)= 6(1)n<4
四、平面最近点问题
将平面点按照x点中位数递归分为两部分,分别两部分中找到最近点,以及是否存在最近两点在交界处两侧。
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
#define MAXN 10000
#define INF 0x7fffffff
struct point{
double x,y;
}a[MAXN];
int N;
int t[MAXN];
//以x坐标大小为关键词
bool cmp1(point x,point y){
return x.x<y.x;
}
//以y坐标大小为关键词
bool cmp2(int x,int y){
return a[x].y<a[y].y;
}
//计算两点距离
double dis(point x,point y){
return sqrt((x.x-y.x)*(x.x-y.x)+(x.y-y.y)*(x.y-y.y));
}
//核心算法 分治思想
double F(int l,int r){
if(r-l==0)
return INF;
if(r-l==1) //如果递归完后直接输出距离
return dis(a[l],a[r]);
int mid=(l+r)>>1;
double ans=min(F(l,mid),F(mid+1,r));
int cnt=0;
for(int i=l;i<=r;i++)
//还有一种情况是距离最小的两点刚好分在mid两端ans距离内的点
if(a[i].x>=a[mid].x-ans&&a[i].x<=a[mid].x+ans)
t[++cnt]=i;
sort(t+1,t+cnt+1,cmp2); //以y坐标大小排序
for(int i=1;i<=cnt;i++)
for(int j=i+1;j<=cnt;j++){
if(a[t[j]].y>=a[t[i]].y+ans) break; //两个点的垂直距离超过ans就不必计算了,显然不可能会成为新的ans
ans=min(ans,dis(a[t[i]],a[t[j]]));
}
return ans;
}
int main(){
cin >> N; //输入坐标数
for(int i=1;i<=N;i++)
cin >> a[i].x >> a[i].y; //输入坐标
sort(a+1,a+N+1,cmp1); //以x坐标大小排序
cout << F(1,N) << endl; //输出最小点对距离
}
五、棋盘覆盖问题
¢ 在一个 2 k × 2 k 个方格组成的棋盘中,若恰有一个方格与其他方格不同,称该方格为特殊方格,且称该棋盘为特殊棋盘( Defective Chessboard )。
令 size =2 k ,表示棋盘的规格。
1. 棋盘:使用二维数组表示
为了方便递归调用,将数组 board 设为全局变量。 board[0][0] 是棋盘的左上角方格。子棋盘:由棋盘左上角的坐标 tr , tc 和棋盘大小 s 表示。
特殊方格:在二维数组中的坐标位置是( dr , dc )。
L 型骨牌:用到的 L 型骨牌个数为 ( 4 k -1)/3 ,将所有 L 型骨牌从 1 开始连续编号,用一个全局变量表示:
static int tile=1;
#include<iostream>
#include<algorithm>
using namespace std;
//棋盘覆盖问题
int board[1025][1025];
static int tile=1;
void ChessBoard(int tr,int tc,int dr,int dc,int size){
if(size==1)return;//递归边界
int t=tile++;//L型骨牌
int s=size/2;//分割棋盘
//覆盖左上角子棋盘
if(dr<tr+s&&dc<tc+s)
//特殊方格在此棋盘中
ChessBoard(tr,tc,dr,dc,s);
else{
//此棋盘中无特殊方格,用t号L型骨牌覆盖右下角
board[tr+s-1][tc+s-1]=t;
//覆盖其余方格
ChessBoard(tr,tc,tr+s-1,tc+s-1,s);
}
//覆盖右上角子棋盘
if(dr<tr+s&&dc>=tc+s)
//特殊方格在此棋盘中
ChessBoard(tr,tc+s,dr,dc,s);
else{
//此棋盘中无特殊方格,用t号L型骨牌覆盖左下角
board[tr+s-1][tc+s]=t;
//覆盖其余方格
ChessBoard(tr,tc+s,tr+s-1,tc+s,s);
}
//覆盖左下角子棋盘
if(dr>=tr+s&&dc<tc+s)
//特殊方格在此棋盘中
ChessBoard(tr+s,tc,dr,dc,s);
else{
//此棋盘中无特殊方格,用t号L型骨牌覆盖右上角
board[tr+s][tc+s-1]=t;
ChessBoard(tr+s,tc,tr+s,tc+s-1,s);
}
//覆盖右下角子棋盘
if(dr>=tr+s&&dc>=tc+s)
//特殊方格在此棋盘中
ChessBoard(tr+s,tc+s,dr,dc,s);
else{
//此棋盘中无特殊方格,用t号L型骨牌覆盖左上角
board[tr+s][tc+s]=t;
//覆盖其余方格
ChessBoard(tr+s,tc+s,tr+s,tc+s,s);
}
}
int main()
{
int n,a,b,aa,bb,length,m;
//a,b是子棋盘左上角的行号和列号
//aa,bb是特殊点的行号和列号
cout<<"请输入1-100之间的整数:";
cin>>length;
cout<<"请输入特殊点行号aa:";
cin>>aa;
cout<<"请输入特殊点列号bb:";
cin>>bb;
a=b=1;
m=length;
ChessBoard(a,b,aa,bb,length);
for(int i=1;i<=m;i++){ //输出结果
for(int j=1;j<=m;j++){
cout.width(3);
cout<<board[i][j];
if(j==m){
cout<<endl;
}
}
}
}六、循环日程赛表

最小单位为 2*2,观察表得4*4的表中对角线上的2*2赛程相同。
运用分治思想,把大表细分为最小单位,安拍完毕各最小单位后,对称排布别的赛程
#include<iostream>
#include<cstdio>
using namespace std;
const int maxn = 10000;
int a[maxn][maxn];
inline void dfs(int n,int k)
{
if(n == 2)
{
a[k][0] = k+1;
a[k][1] = k+2;
a[k+1][0] = k+2;
a[k+1][1] = k+1;
}
else
{
dfs(n/2,k);
dfs(n/2,k+n/2);
for(int i = k; i < k+n/2; i++)
{
for(int j = n/2; j < n; j++) a[i][j] = a[i+n/2][j-n/2];
}
for(int i = k+n/2; i < k+n; i++)
{
for(int j = n/2; j < n; j++) a[i][j] = a[i-n/2][j-n/2];
}
}
}
int main()
{
int n;
cin>>n;
dfs(n,0);
for(int i = 0; i < n; i++)
{
for(int j = 0; j < n; j++) printf("%d ",a[i][j]);
printf("\n");
}
return 0;
}
七、大整数乘法
问题描述:假设有两个大整数X、Y,分别设X=1234、Y=6789。现在要求X*Y的乘积,小学的算法就是把X与Y中的每一项去乘,但是这样的乘法所需的时间复杂度为O(N^2),(因为每一位要逐个去乘),所以效率比较低下。那我们可以采用分治的算法,将X、Y拆分成四部分,如下图:

则X可表示为:

同理Y也可以表示出来。
所以现在将一个大的整数分成了两部分,问题规模减小,这样直接相乘就会写成


#include<iostream>
#include<cmath>
using namespace std;
int divideConquer(int X, int Y, int n){
int x = abs(X);
int y = abs(Y);
if( x == 0 || y == 0){
return 0;
}else if( n == 1){
return x * y;
}else{
int A = x / pow(10, n / 2);
int B = x - A * pow(10, n / 2);
int C = y / pow(10, n / 2);
int D = y - C * pow(10, n / 2);
int AC = divideConquer(A, C, n / 2);
int BD = divideConquer(B, D, n / 2);
int ABCD = divideConquer((A - B), (D - C), n / 2) + AC + BD;
return AC*pow(10, n) + ABCD * pow(10, n / 2) + BD;
}
}
int main(){
cout << divideConquer(1234, 9876, 4) << endl;
return 0;
}



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








