简介
贝叶斯网络(Bayesian network),又称信念网络(belief network)或是有向无环图模型(directed acyclic graphical model),是一种概率图型模型,借由有向无环图(directed acyclic graphs, or DAGs )中得知一组随机变量{}及其n组条件概率分配(conditional probability distributions, or CPDs)的性质。一般而言,贝叶斯网络的有向无环图中的节点表示随机变量,它们可以是可观察到的变量,抑或是隐变量、未知参数等。连接两个节点的箭头代表此两个随机变量是具有因果关系或是非条件独立的;而节点中变量间若没有箭头相互连接一起的情况就称其随机变量彼此间为条件独立。若两个节点间以一个单箭头连接在一起,表示其中一个节点是“因(parents)”,另一个是“果(descendants or children)”,两节点就会产生一个条件概率值。比方说,我们以表示第i个节点,而
的“因”以
表示,
的“果”以
表示;图1就是一种典型的贝叶斯网络结构图,依照先前的定义,我们就可以轻易的从图1可以得知:
-
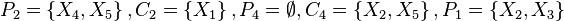 ,以及
,以及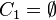
图 1
大部分的情况下,贝叶斯网络适用在节点的性质是属于离散型的情况下,且依照此条件概率写出条件概率表,写出条件概率表后就很容易将事情给条理化,且轻易地得知此贝叶斯网络结构图中各节点间之因果关系;但是条件概率表也有其缺点:若是节点
是由很多的“因”所造成的“果”,如此条件概率表就会变得在计算上既复杂又使用不便。
数学定义
令G = (I,E)表示一个有向无环图(DAG),其中I代表图形中所有的节点的集合,而E代表有向连接线段的集合,且令X = (Xi)i ∈ I为其有向无环图中的某一节点i所代表之随机变量,若节点X的联合概率分配可以表示成:
则称X为相对于一有向无环图G 的贝叶斯网络,其中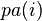 表示节点i之“因”。
表示节点i之“因”。
对任意的随机变量,其联合分配可由各自的局部条件概率分配相乘而得出:
依照上式,我们可以将一贝叶斯网络的联合概率分配写成:
-
 , 对每个相对于X
i的“因”变量X
j
而言)
, 对每个相对于X
i的“因”变量X
j
而言)
上面两个表示式之差别在于条件概率的部分,在贝叶斯网络中,若已知其“因”变量下,某些节点会与其“因”变量条件独立,只有与“因”变量有关的节点才会有条件概率的存在。如果联合分配的相依数目很稀少时,使用贝氏函数的方法可以节省相当大的存储器容量。举例而言,若想将10个变量其值皆为0或1存储成一条件概率表型式,一个直观的想法可知我们总共必须要计算 个值;但若这10个变量中无任何变量之相关“因”变量是超过三个以上的话,则贝叶斯网络的条件概率表最多只需计算
个值;但若这10个变量中无任何变量之相关“因”变量是超过三个以上的话,则贝叶斯网络的条件概率表最多只需计算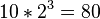 个值即可!另一个贝式网络优点在于:对人类而言,它更能轻易地得知各变量间是否条件独立或相依与其局部分配(local distribution)的型态来求得所有随机变量之联合分配。
个值即可!另一个贝式网络优点在于:对人类而言,它更能轻易地得知各变量间是否条件独立或相依与其局部分配(local distribution)的型态来求得所有随机变量之联合分配。
马尔可夫毯(Markov blanket)
马尔科夫毯,是满足如下特性的一个最小特征子集:一个特征在其马尔科夫毯条件下,与特征域中所有其他特征条件独立。设特征T的马尔科夫毯为MB(T),则上述可表示为:
P(T | MB(T)) = P(T | Y, MB(T))
其中Y为特征域中的所有非马尔科夫毯结点。这是马尔科夫毯的最直接的定义。关于某一特征的马尔科夫毯在贝叶斯网络中的表现形式是该特征(即该结点)的父结点、子结点以及子结点的父结点。
举例说明
假设有两个服务器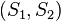 ,会传送数据包到用户端 (以U表示之),但是第二个服务器的数据包传送成功率会与第一个服务器传送成功与否有关,因此此贝叶斯网络的结构图可以表示成如图2的型式。就每个数据包传送而言,只有两种可能值:T(成功) 或 F(失败)。则此贝叶斯网络之联合概率分配可以表示成:
,会传送数据包到用户端 (以U表示之),但是第二个服务器的数据包传送成功率会与第一个服务器传送成功与否有关,因此此贝叶斯网络的结构图可以表示成如图2的型式。就每个数据包传送而言,只有两种可能值:T(成功) 或 F(失败)。则此贝叶斯网络之联合概率分配可以表示成:
图 2
此模型亦可回答如:“假设已知用户端成功接受到数据包,求第一服务器成功发送数据包的概率?”诸如此类的问题,而此类型问题皆可用条件概率的方法来算出其所求之发生概率:
该例中网络的结构已知,只需根据观测值得到概率表,再根据概率表及联合概率公式计算
求解方法
以上例子是一个很简单的贝叶斯网络模型,但是如果当模型很复杂时,这时使用枚举式的方法来求解概率就会变得非常复杂且难以计算,因此必须使用其他的替代方法。一般来说,贝氏概率有以下几种求法:
精确推理
- 枚举推理法(如上述例子)只适用于简单的网络
- 变量消元算法(variable elimination)
随机推理(蒙特卡洛方法)
- 直接取样算法
- 拒绝取样算法
- 概似加权算法
- 马尔可夫链蒙特卡洛算法(Markov chain Monte Carlo algorithm)
在此,以马尔可夫链蒙特卡洛算法为例,又马尔可夫链蒙特卡洛算法的类型很多,故在这里只说明其中一种Gibbs sampling的操作步骤: 首先将已给定数值的变量固定,然后将未给定数值的其他变量随意给定一个初始值,接着进入以下迭代步骤:
- (1)随意挑选其中一个未给定数值的变量
-
(2)从条件分配
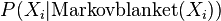 抽样出新的
抽样出新的 的值,接着重新计算
的值,接着重新计算
-
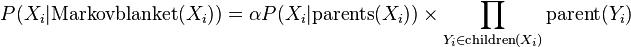
当迭代退出后,删除前面若干笔尚未稳定的数值,就可以求出 的近似条件概率分配。马尔可夫链蒙特卡洛算法的优点是在计算很大的网络时效率很好,但缺点是所抽取出的样本并不具独立性。
当贝叶斯网络上的结构跟参数皆已知时,我们可以通过以上方法来求得特定情况的概率,不过,如果当网络的结构或参数未知时,我们必须借由所观测到的数据去推估网络的结构或参数,一般而言,推估网络的结构会比推估节点上的参数来的困难。依照对贝叶斯网络结构的了解和观测值的完整与否,我们可以分成下列四种情形:
| 结构 | 观测值 | 方法 |
|---|---|---|
| 已知 | 完整 | 最大似然估计法 (MLE) |
| 已知 | 部份 | EM 算法 Greedy Hill-climbing method |
| 未知 | 完整 | 搜索整个模型空间 |
| 未知 | 部份 | 结构算法 EM 算法 Bound contraction |
以下就结构已知的部分,作进一步的说明。
1. 结构已知,观测值完整:
此时我们可以用最大似然估计法(MLE)来求得参数。其对数概似函数为
其中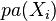 代表
代表 的因变量,
的因变量, 代表第
代表第 个观测值,N代表观测值数据的总数。
个观测值,N代表观测值数据的总数。
以图二当例子,我们可以求出节点U的最大似然估计式为
由上式就可以借由观测值来估计出节点U的条件分配。如果当模型很复杂时,这时可能就要利用数值分析或其它最优化技巧来求出参数。
2. 结构已知,观测值不完整(有遗漏数据):
如果有些节点观测不到的话,可以使用EM算法(Expectation-Maximization algorithm)来决定出参数的区域最佳概似估计式。而EM算法的的主要精神在于如果所有节点的值都已知下,在M阶段就会很简单,如同最大似然估计法。而EM算法的步骤如下:
(1)首先给定欲估计的参数一个起始值,然后利用此起始值和其他的观测值,求出其他未观测到节点的条件期望值,接着将所估计出的值视为观测值,将此完整的观测值带入此模型的最大似然估计式中,如下所示(以图二为例):
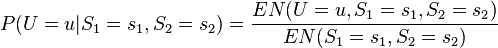
其中 代表在目前的估计参数下,事件x 的条件概率期望值为
代表在目前的估计参数下,事件x 的条件概率期望值为
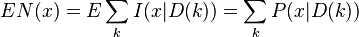
(2)最大化此最大似然估计式,求出此参数之最有可能值,如此重复步骤(1)与(2),直到参数收敛为止,即可得到最佳的参数估计值。
参考
wikipedia--贝叶斯网络
百度知道









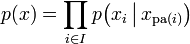
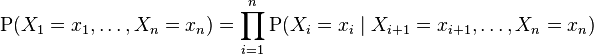
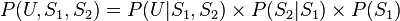

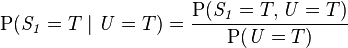
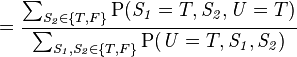
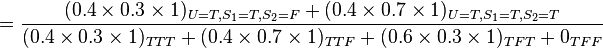


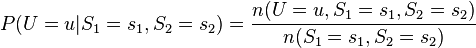
















 1279
1279

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








