| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 10278 | Accepted: 4946 |
Description
Some cows like each other and want to be within a certain distance of each other in line. Some really dislike each other and want to be separated by at least a certain distance. A list of ML (1 <= ML <= 10,000) constraints describes which cows like each other and the maximum distance by which they may be separated; a subsequent list of MD constraints (1 <= MD <= 10,000) tells which cows dislike each other and the minimum distance by which they must be separated.
Your job is to compute, if possible, the maximum possible distance between cow 1 and cow N that satisfies the distance constraints.
Input
Lines 2..ML+1: Each line contains three space-separated positive integers: A, B, and D, with 1 <= A < B <= N. Cows A and B must be at most D (1 <= D <= 1,000,000) apart.
Lines ML+2..ML+MD+1: Each line contains three space-separated positive integers: A, B, and D, with 1 <= A < B <= N. Cows A and B must be at least D (1 <= D <= 1,000,000) apart.
Output
Sample Input
4 2 1
1 3 10
2 4 20
2 3 3
Sample Output
27
Hint
There are 4 cows. Cows #1 and #3 must be no more than 10 units apart, cows #2 and #4 must be no more than 20 units apart, and cows #2 and #3 dislike each other and must be no fewer than 3 units apart.
The best layout, in terms of coordinates on a number line, is to put cow #1 at 0, cow #2 at 7, cow #3 at 10, and cow #4 at 27.
Source
题目大意:
一共有n头牛,有ml个关系好的牛的信息,有md个关系不好的牛的信息,对应输入的第一行的三个元素,接下来ml行,每行三个元素A,B,D,表示A牛和B牛相距不希望超过D,接下来md行,每行三个元素A,B,D表示A牛和B牛的相距至少要有D才行。求1号牛和n号牛的最大距离,如果距离无限大输出-2,如果无解输出-1。
思路:
1、因为我们要求1号牛和n号牛的最大距离,那么我们希望得到这样一个不等式(假设n==5):①-⑤<=x,那么这个x就是1号牛和n号牛的最大距离。
2、那么我们引入一个差分约束系统的相关概念:
差分约束系统问题,能够将问题转化为最短路问题。以下给出转化过程:
假设有这样的三个条件:
那么我们可以将不等式1和不等式2相加得到:
那么如果想要得到x1和x3的最大差值,那么其实就是取min(k1+k2,k3);
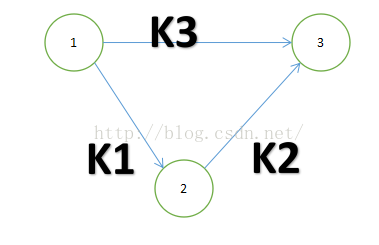
其实问题我们可以将问题转化成图论,将x1,x2,x3看成三个点x1,x2,x3,对应三条边的建立就根据三个不等式来建立,那么边权值如何取呢?显然我们想要最大差值,我们就需要取最大值,那么图可以建立成这样:
那么我们上述过程将不等式1和不等式2相加,然后和不等式3比较值的过程,其实就是最短路计算过程中的判断能否松弛的过程。
那么我们就可以根据不等式建立有向图,然后再通过有向图计算1号点到n号点的最短路,其值就是x1与xn的最大差值。
3、然后我们再回归到这个问题上来。
对应ml条信息:
①牛A和牛B的距离不想超过D,那么建立不等式:posA-posB<=D;加入到图中直接add(A,B,D)即可、
对应md条信息:
②牛A和牛B的距离至少要为D,那么建立不等式:posA-posB>=D,那么我们左右两边同乘-1有:posB-posA<=-D,那么加入到图中add(B,A,-D)即可。
4、图建立好之后直接跑最短路即可。
对应输出:
①如果dis【n】==inf,输出-2;
②否则输出dis【n】;
③如果在跑SPFA过程中发现了负环,说明问题无解,那么输出-1.
Ac代码:
#include<stdio.h>
#include<string.h>
#include<queue>
using namespace std;
struct node
{
int from;
int to;
int w;
int next;
}e[200000];
int head[10000];
int vis[10000];
int out[10000];
int dis[10000];
int n,ml,dl,cont;
void add(int from,int to,int w)
{
e[cont].to=to;
e[cont].w=w;
e[cont].next=head[from];
head[from]=cont++;
}
void SPFA()
{
for(int i=1;i<=n;i++)dis[i]=0x3f3f3f3f;
dis[1]=0;
memset(vis,0,sizeof(vis));
memset(out,0,sizeof(out));
queue<int >s;
s.push(1);
int flag=0;
while(!s.empty())
{
int u=s.front();
out[u]++;
if(out[u]>n)
{
flag=1;
break;
}
s.pop();
vis[u]=0;
for(int i=head[u];i!=-1;i=e[i].next)
{
int v=e[i].to;
int w=e[i].w;
if(dis[v]>dis[u]+w)
{
dis[v]=dis[u]+w;
if(vis[v]==0)
{
vis[v]=1;
s.push(v);
}
}
}
}
if(flag==1)
{
printf("-1\n");
}
else if(dis[n]==0x3f3f3f3f)printf("-2\n");
else printf("%d\n",dis[n]);
}
int main()
{
while(~scanf("%d%d%d",&n,&ml,&dl))
{
cont=0;
memset(head,-1,sizeof(head));
for(int i=0;i<ml;i++)
{
int x,y,w;
scanf("%d%d%d",&x,&y,&w);
add(x,y,w);
}
for(int i=0;i<dl;i++)
{
int x,y,w;
scanf("%d%d%d",&x,&y,&w);
add(y,x,-w);
}
SPFA();
}
}








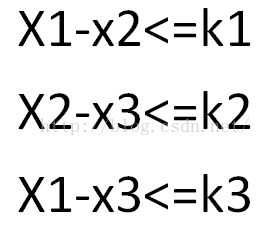















 97
97

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








