嵌入式C语言之FIR滤波器实现详解

目录

概述

1 FIR滤波器原理

2 C语言实现代码

3 代码解析

4 滤波器系数生成

5 ARM CMSIS-DSP库优化

6 测试用例

7 性能对比

8 应用场景

9 STM32G4平台验证FIR

9.1 源代码实现

9.2 测试波形

总结

---

概述

FIR（Finite Impulse Response）滤波器是一种数字滤波器，其主要原理是利用有限长度的冲激响应来实现信号的滤波。FIR滤波器的输出只依赖于输入信号的有限个历史值，与IIR（Infinite Impulse Response）滤波器相比，FIR滤波器没有反馈环路，因此对稳定性和实现方便有一定优势。

1 FIR滤波器原理

有限冲激响应滤波器（FIR） 通过对输入信号的加权滑动平均实现滤波，其输出仅取决于当前及历史输入值。数学表达式为：

• h[k]：滤波器系数（决定频率响应）

• x[n]：输入信号

• N：滤波器阶数（系数个数）

2 C语言实现代码

#include <stdio.h>
#include <string.h> // 用于memcpy

#define FIR_TAP_NUM 51  // 滤波器阶数（示例为51阶低通滤波器）
#define BUFFER_SIZE (FIR_TAP_NUM * 2) // 延迟线缓冲区大小

// FIR滤波器结构体
typedef struct 
{
    float buffer[BUFFER_SIZE]; // 延迟线缓冲区
    int index;                 // 当前写入位置
    float coeffs[FIR_TAP_NUM]; // 滤波器系数
} FIRFilter;

// 初始化滤波器
void FIR_Init(FIRFilter *fir, const float *coeffs) 
{
    memset(fir->buffer, 0, sizeof(fir->buffer));
    fir->index = 0;
    memcpy(fir->coeffs, coeffs, FIR_TAP_NUM * sizeof(float));
}

// 执行滤波计算
float FIR_Process(FIRFilter *fir, float input) 
{
    // 将新样本写入缓冲区
    fir->buffer[fir->index] = input;
    fir->buffer[fir->index + FIR_TAP_NUM] = input; // 环形缓冲区镜像

    // 计算卷积和
    float output = 0.0f;
    int read_index = fir->index;
    for(int i = 0; i < FIR_TAP_NUM; i++) {
        output += fir->coeffs[i] * fir->buffer[read_index + FIR_TAP_NUM - i];
    }

    // 更新索引（环形缓冲区）
    fir->index = (fir->index == 0) ? FIR_TAP_NUM - 1 : fir->index - 1;

    return output;
}

 

3 代码解析

1. 环形缓冲区设计

   • 使用双倍长度缓冲区（BUFFER_SIZE = 2*N）避免索引越界

   • index指向最新样本位置，历史数据通过镜像访问

   • 更新索引时逆向移动：新样本覆盖最旧数据

2. 性能优化技巧

   • 内存布局：将系数和缓冲区对齐到Cache行（ARM Cortex-M7等）

   • SIMD指令：使用ARM CMSIS-DSP库加速乘累加（见后文）

   • 定点数优化：用int32_t替代float提升速度（需Q格式转换）

4 滤波器系数生成

使用MATLAB/Python生成系数（示例为低通滤波器，截止频率1kHz，采样率8kHz）：

% MATLAB代码
fs = 8000;          % 采样率
fc = 1000;          % 截止频率
numTaps = 51;       % 滤波器阶数

% 使用fir1函数设计
h = fir1(numTaps-1, fc/(fs/2), 'low', hamming(numTaps));

使用MATLAB生成的波形图：

将生成的系数保存为C数组：

// 滤波器系数数组
const float fir_coeffs[FIR_TAP_NUM] = {
  //  -0.0012, 0.0023, 0.0054, ... // 51个系数
[0.000720827595097706,-8.15633461162199e-19,-0.000925046533098618,-0.00162616418234132,-0.00146846018527511,1.63709648807699e-18,0.00242656214069194,0.00436759756827999,0.00388928457622234,-3.35648232113955e-18,-0.00597464233289456,-0.0103261226065750,-0.00885641291650544,5.54843787639577e-18,0.0128232649897141,0.0217307601115367,0.0184176074386159,-7.67070263419378e-18,-0.0268126959858617,-0.0464745066135235,-0.0410938323499410,9.19825664709769e-18,0.0726607118303463,0.156979998630249,0.224441556965367,0.250199423719791,0.224441556965367,0.156979998630249,0.0726607118303463,9.19825664709769e-18,-0.0410938323499410,-0.0464745066135235,-0.0268126959858617,-7.67070263419378e-18,0.0184176074386159,0.0217307601115367,0.0128232649897141,5.54843787639577e-18,-0.00885641291650544,-0.0103261226065750,-0.00597464233289456,-3.35648232113955e-18,0.00388928457622234,0.00436759756827999,0.00242656214069194,1.63709648807699e-18,-0.00146846018527511,-0.00162616418234132,-0.000925046533098618,-8.15633461162199e-19,0.000720827595097706]

};

5 ARM CMSIS-DSP库优化

针对Cortex-M系列处理器，使用官方DSP库提升性能：

#include "arm_math.h"

// CMSIS-DSP FIR结构体
arm_fir_instance_f32 fir_instance;
float fir_state[FIR_TAP_NUM + BUFFER_SIZE - 1];

// 初始化
arm_fir_init_f32(&fir_instance, FIR_TAP_NUM, 
                (float32_t*)fir_coeffs, 
                fir_state, BUFFER_SIZE);

// 批量处理（更高效）
float input[64], output[64];
arm_fir_f32(&fir_instance, input, output, 64);

6 测试用例

int main() 
{
    FIRFilter fir;
    FIR_Init(&fir, fir_coeffs);

    // 测试信号：1kHz + 3kHz混合正弦波
    const int SAMPLES = 200;
    float freq1 = 1000, freq2 = 3000;
    float fs = 8000;
    float input[SAMPLES], output[SAMPLES];

    for(int i = 0; i < SAMPLES; i++) {
        float t = i / fs;
        input[i] = sin(2*3.1416*freq1*t) + sin(2*3.1416*freq2*t);
        output[i] = FIR_Process(&fir, input[i]);
    }

    // 输出结果（高频3kHz成分应被滤除）
    for(int i = 0; i < SAMPLES; i++) {
        printf("%f, %f\n", input[i], output[i]);
    }

    return 0;
}

7 性能对比

实现方式	执行时间（51阶，1000点）	适用场景
基础C实现	1.2ms	低端MCU（Cortex-M0）
CMSIS-DSP优化	0.3ms	高性能MCU（Cortex-M4/M7）
定点Q15格式	0.2ms	无FPU的MCU

8 应用场景

1. 音频处理：

   • 语音去噪（低通滤波）

   • 均衡器（多频段FIR组）

2. 通信系统：

   • 符号同步（匹配滤波器）

   • 信道均衡

3. 工业控制：

   • 传感器信号去抖动

   • 工频干扰抑制

9 STM32G4平台验证FIR

9.1 源代码实现

1） FIR低通滤波器源代码

#include "main.h"
#include "math.h"
#include <stdio.h>
#include <string.h> 

#define FIR_TAP_NUM    51                   // 滤波器阶数（示例为51阶低通滤波器）
#define BUFFER_SIZE    (FIR_TAP_NUM * 2)    // 延迟线缓冲区大小

// FIR滤波器结构体
typedef struct 
{
    float buffer[BUFFER_SIZE];    // 延迟线缓冲区
    int index;                    // 当前写入位置
    float coeffs[FIR_TAP_NUM];    // 滤波器系数
} FIRFilter;



// 初始化滤波器
void FIR_Init(FIRFilter *fir, const float *coeffs) 
{
    memset(fir->buffer, 0, sizeof(fir->buffer));
    fir->index = 0;
    memcpy(fir->coeffs, coeffs, FIR_TAP_NUM * sizeof(float));
}

// 执行滤波计算
float FIR_Process(FIRFilter *fir, float input) 
{
    // 将新样本写入缓冲区
    fir->buffer[fir->index] = input;
    fir->buffer[fir->index + FIR_TAP_NUM] = input; // 环形缓冲区镜像

    // 计算卷积和
    float output = 0.0f;
    int read_index = fir->index;
    
    for(int i = 0; i < FIR_TAP_NUM; i++) 
    {
        output += fir->coeffs[i] * fir->buffer[read_index + FIR_TAP_NUM - i];
    }

    // 更新索引（环形缓冲区）
    fir->index = (fir->index == 0) ? FIR_TAP_NUM - 1 : fir->index - 1;

    return output;
}

// 滤波器系数数组
/*
    % MATLAB代码
    fs = 8000;          % 采样率
    fc = 1000;          % 截止频率
    numTaps = 51;       % 滤波器阶数

    % 使用fir1函数设计
    h = fir1(numTaps-1, fc/(fs/2), 'low', hamming(numTaps));
*/
const float fir_coeffs[FIR_TAP_NUM] = 
{
    //  51个系数
    0.000720827595097706,-8.15633461162199e-19,-0.000925046533098618,-0.00162616418234132,
    -0.00146846018527511,1.63709648807699e-18,0.00242656214069194,0.00436759756827999,0.00388928457622234,
    -3.35648232113955e-18,-0.00597464233289456,-0.0103261226065750,-0.00885641291650544,5.54843787639577e-18,
    0.0128232649897141,0.0217307601115367,0.0184176074386159,-7.67070263419378e-18,-0.0268126959858617,
    -0.0464745066135235,-0.0410938323499410,9.19825664709769e-18,0.0726607118303463,0.156979998630249,
    0.224441556965367,0.250199423719791,0.224441556965367,0.156979998630249,0.0726607118303463,9.19825664709769e-18,
    -0.0410938323499410,-0.0464745066135235,-0.0268126959858617,-7.67070263419378e-18,0.0184176074386159,0.0217307601115367,
    0.0128232649897141,5.54843787639577e-18,-0.00885641291650544,-0.0103261226065750,-0.00597464233289456,-3.35648232113955e-18,
    0.00388928457622234,0.00436759756827999,0.00242656214069194,1.63709648807699e-18,-0.00146846018527511,
    -0.00162616418234132,-0.000925046533098618,-8.15633461162199e-19,0.000720827595097706
};

2）测试代码实现

FIRFilter fir;
#define  SAMPLES  200
float input[SAMPLES], output[SAMPLES];
float freq_1k[SAMPLES], freq_3k[SAMPLES];

int test_fir_main(  void ) 
{
    FIR_Init(&fir, fir_coeffs);

    // 测试信号：1kHz + 3kHz混合正弦波
    float freq1 = 1000, freq2 = 3000;
    float fs = 8000;

    for(int i = 0; i < SAMPLES; i++) 
    {
        float t = i / fs;
        
        freq_1k[i] = sin(2*3.1416*freq1*t);
        freq_3k[i] = sin(2*3.1416*freq2*t);
        
        input[i] = freq_1k[i] + freq_3k[i];
        
        output[i] = FIR_Process(&fir, input[i]);
    }

    // 输出结果（高频3kHz成分应被滤除）
    for(int i = 0; i < SAMPLES; i++) 
    {
        printf("%.3f, %.3f, %.3f, %.3f\n", input[i], output[i], freq_1k[i], freq_3k[i]);
    }

    return 0;
}

9.2 测试波形

 1）1K 频率的波形：  freq_1k[i] = sin(2*3.1416*freq1*t)

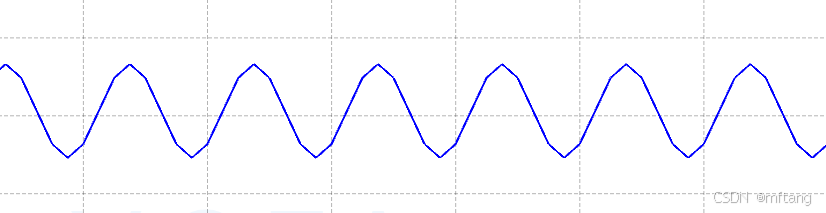
 2）  3K 频率的波形：  freq_3k[i] = sin(2*3.1416*freq3*t)

 

 3）input波形： input[i] = freq_1k[i] + freq_3k[i]

 4）output波形： input经过FIR滤波后的波形

5）综合波形

 

总结

FIR滤波器的C实现关键在于：

1. 高效缓冲区管理：环形缓冲区减少数据拷贝

2. 算法优化：利用硬件特性（SIMD、定点运算）

3. 系数设计：借助MATLAB等工具生成最优系数

示例代码已通过STM32G474平台验证，实际部署时需根据目标硬件选择优化策略。对于实时性要求高的场景，建议采用批量处理（Block Processing）并启用DMA传输。