今天要总结的是图的迪杰斯特拉算法。这个算法是针对有向带权图的,求的是图中某一个定点到其余所有顶点的最短路径。
下面说说这个算法的基本思想吧:设定两个集合A和B,A中存放我们已经处理过的顶点,B中存放图中剩余顶点。刚开始的时候,A中只有一个我们选定的起点v0,每一次从集合B中取到v0的代价最小的点并入,每一次并入时都需要修改v0到B中顶点的代价,直到所有的顶点都并入为止。
算法准备:
1、数组dist,用于存放v0到图中个顶点的代价,数组下标表示顶点编号
2、数组path,用于存放路径,数组下标表示顶点编号,下标所对应的数组值表示能够到达当前这个顶点的前一个顶点编号,最后连起来就是v0到图中各顶点的最短路径了。如果没有前前驱顶点,则内容值为-1。
3、数组set,用于标识图中顶点是否被处理过,数组下标表示顶点编号。处理过为1,没处理过为0。
4、使用图的邻接矩阵来存储有向带权图,graph[i][j]。
算法过程(我们选择编号为0的顶点作为起点):
1、首先进行3个数组的初始化,把set数组全部初始化为0;dist数组全部初始化为无穷大,path数组全部初始化为-1。
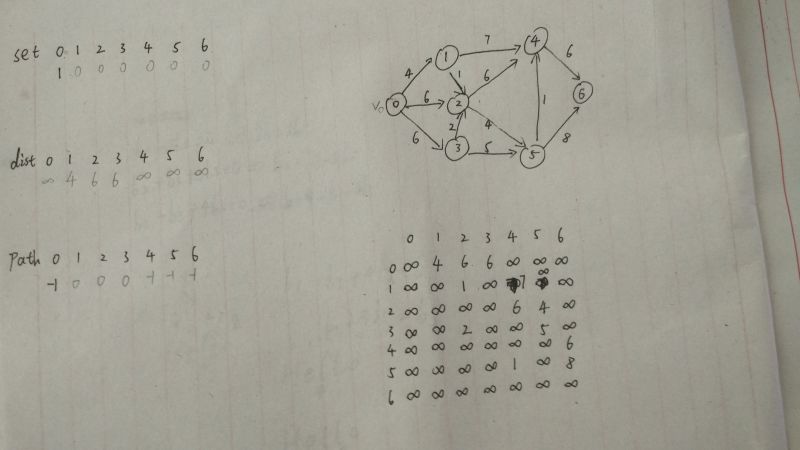
2、将set[0]的值设置为1,然后遍历邻接矩阵的第0行,依次更新dist数组的每一项。
3、将dist数组中值不为无穷大的在path中的对应下标,把它们的值改为0。因为编号为0的点是它们的前驱嘛。如下图:
4、选择dist数组中值最小的点的下标,这里为1。
5、将set[1]的值设置为1
6、遍历邻接矩阵的第1行(因为1是最小权值的下标),将dist[1]的值与邻接矩阵graph[1][i]的值相加(此时是以编号为1的点作为中间点,看看由v0->v1再到其余点的路径长度会不会比v0直接到它们的路径长度短),如果这个值比dist[i]的值小,就更新dist[i],同时将path[i]的值设置为1,执行这个操作的前提是,set[i]为0。操作完成后如下图:
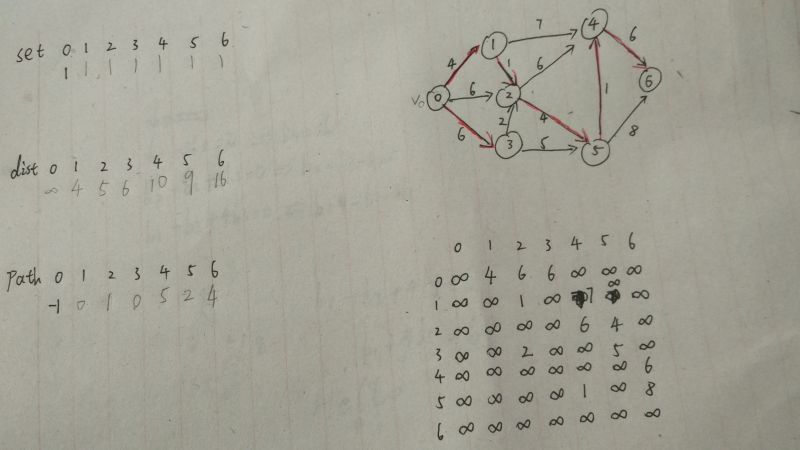
7、重复【4】~【6】步,如果已经处理过的点就不用再判断了。直到set数组全变为1。最后如下图
现在,我们就可以看出最短路径了。
比如v0到v6的路径为,注意path数组,从下标6的位置开始看起,逐级向上查找,直到遇到-1为止
v6->v4->v5->v2->v1->v0
有没有发现这个是逆序的呢?根据后进先出的原则,我们想到输出要用到栈。
下面上代码:
1、首先是图的结构体定义
#define Max 100
typedef struct graph *Graph;
typedef struct graph
{
int data[30][30];
int n , e;
}graph;
void Dijkstra(Graph g , int v , int path[] , int dist[])
{
int set[Max];
//initial
int i , j;
for(i = 0 ; i < g->n ; i++)
{
set[i] = 0;
dist[i] = g->data[v][i];
if(g->data[v][i] < Max)
{
path[i] = v;
}
else
{
path[i] = -1;
}
}
set[0] = 1;
path[0] = -1;
//main
for(i = 1 ; i<= g->n-1 ; i++)
{
int min = Max;
int minP = 0;
for(j = 0 ; j < g->n ; j++)
{
if(set[j] == 0 && dist[j] < min)
{
min = dist[j];
minP = j;
}
}
set[minP] = 1;
for(j = 0 ; j < g->n ; j++)
{
if(set[j] == 0 && g->data[minP][j] + min < dist[j])
{
dist[j] = g->data[minP][j] + min;
path[j] = minP;
}
}
}
}b、在初始化path数组的过程中,如果某个顶点在邻接矩阵v行的值不为无穷大,说明该点可以由v到达,所以将该path数组中的值设置成v,而在矩阵中v行值为无穷大的,就设置成-1。
3、输出路径代码
void showPath(int path[], int begin)
{
int stack[Max];
int top = -1;
int i = begin;
int flag = 0;
while(path[begin] != -1)
{
stack[++top] = begin;
begin = path[begin];
}
stack[++top] = begin;
if(top == 0)
{
printf("v%d 无最短路径",stack[top]);
return;
}
while(top != -1)
{
if(!flag)
{
printf("v%d",stack[top]);
flag++;
}
else
printf("->v%d",stack[top]);
top--;
}
}

























 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








