AI开发：什么是“模型”？手搓一个【模型】来学习一下 - Python 机器学习

在 AI 学习中，"模型" 就是一个通过数据学习并能够做出预测或决策的工具。它就像是一个大脑，能够从你给它的数据中找到规律，并用这些规律来处理新的信息。

举个简单的例子：假设你要教 AI 判断图片里是不是猫。你可以给它大量标记了"猫"和"非猫"标签的图片，通过这些图片让 AI 学习。AI 会根据这些图片里的特点（比如猫的耳朵形状、眼睛、毛发等）找到规律。这些规律就形成了 AI 的“模型”。当你给它一张新的图片时，AI 就可以利用这些规律来判断它是不是猫。

简而言之，模型就是 AI 学习后得到的一个“思考方式”，它可以根据已有的经验，帮助 AI 做出判断。

从最原始的本质上来理解，一个函数，就是一个“模型”，比如：

def model_test(x):
    return x>5
    
print(model_test(6))

解释：

model_test 是一个非常简单的“模型”。
它接受一个输入 x，并通过 x > 5 判断这个输入是否大于 5。如果 x 大于 5，返回 True，否则返回 False。
在这个例子中，x = 6 时，输出为 True，因为 6 大于 5。

尽管这个函数很简单，但它依然可以视为某种形式的模型。它通过对输入进行判断，得出了一个结果，这就是模型最基本的工作方式。

当然，在这个“模型”中，没有任何可调的参数和训练。

接下来我们来看一个完整模型的流程是怎么样的。

最后又完整代码，可以复制运行一下先，再回过头来看分解。

我们将演示一个非常简单的模型，具体的步骤是使用 Python 来创建一个模型，判断一个数字是否大于 5。这个模型会根据一些已经知道的数据（例如数字和标签）来进行学习，然后用它来判断新的数字。

步骤：

准备一些训练数据：我们给出一组数字，并告诉模型这些数字是否大于 5。
让模型学习这些数据：在这个简单的模型中，我们将“学习”如何从数字判断它是否大于 5。
使用模型来预测新的数据：给模型一个新数字，让它判断这个数字是否大于 5。

流程图：

每个步骤的含义：

初始化模型：在这个步骤中，我们设置模型的初始参数（权重 w 和偏置 b），一般初始化为随机值或者零。
这个步骤是模型训练的起点。
前向传播：输入数据进入模型进行预测，计算出预测值。
损失计算：通过预测值和实际标签计算损失（例如交叉熵损失）。这是模型训练的核心，通过这个损失来衡量模型的好坏。
计算梯度：基于损失函数，计算出关于模型参数（权重和偏置）的梯度。这是通过反向传播来完成的。
更新权重和偏置：使用梯度下降法更新模型参数，即根据计算出的梯度调整 w 和 b，目的是减少损失。
重复训练：步骤 2 到 5 会重复多次，直到达到设定的训练轮次或模型损失趋于稳定。
保存模型：在训练完成后，保存模型的最终参数（假设是 w 和 b）。这使得模型在下次运行时无需重新训练，可以直接加载使用。
进行预测：使用训练好的模型来对新数据进行预测。模型已经通过训练学会了如何做出预测。

将上述的流程进行基本的分解，产生下一个流程图，我们的程序即将按照这个流程展开：

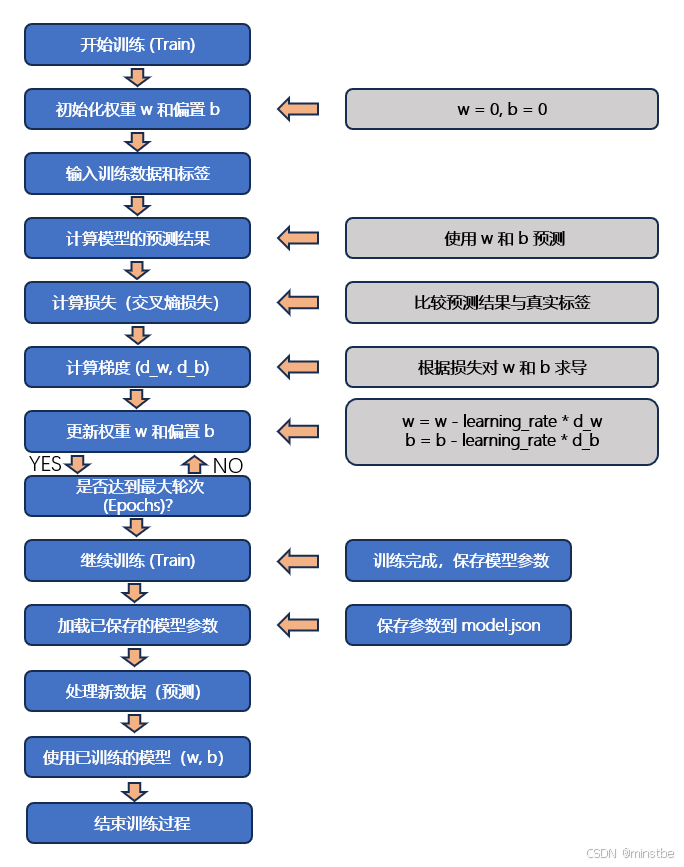
流程图说明：

初始化阶段：模型开始时的权重 w 和偏置 b 被初始化为某个值（例如：0）。之后进入训练过程。
输入训练数据和标签：模型逐个输入训练数据进行预测，同时计算损失。
损失计算和梯度更新：计算损失后，通过求梯度更新模型参数 w 和 b，然后返回继续训练，直到达到预定的训练轮数（epochs）。
保存模型：训练完成后，保存当前的模型参数（w 和 b）到文件 model.json 中。之后运行程序时，可以加载这个模型继续进行预测。
加载模型：如果 model.json 文件存在，程序将加载之前保存的模型参数，避免重新训练。否则，程序开始新的训练过程。

接下来我会详细解释这个例程中每段计算步骤的原理和作用。整个过程的核心目标是使用 逻辑回归 来通过数据训练一个模型，使其能够判断输入的数字是否大于 5。我们会从数据准备、模型训练、损失函数计算到最终预测逐步分析每个步骤。

1. 准备训练数据

train_data = np.array([1, 3, 5, 7, 9, 11])
labels = np.array([0, 0, 0, 1, 1, 1])

train_data: 这是模型的输入数据，即你想要模型进行预测的数字。我们选择了一些小于和大于 5 的数字（这类似我们在图像识别中的原始素材）。
labels: 这些是与每个输入对应的正确输出（标签）。在这个例子中，0 代表数字小于或等于 5，而 1 代表数字大于 5（这类似我们在图像识别中的对素材进行人工标注）。

2. 初始化权重和偏置

w = 0  # 权重
b = 0  # 偏置
learning_rate = 0.1
epochs = 1000

w 和 b: 这是我们要优化的两个参数，分别是权重和偏置。在训练过程中，这两个参数将通过梯度下降法被不断更新，以最小化预测与实际标签之间的误差。（具体了解一下概念就行了，参数会根据函数和输入自动更新的）
learning_rate: 学习率，控制每次更新参数的步长。学习率过大会导致过度跳跃，学习率过小则可能导致收敛过慢。（这个可以根据实际手动来调整）
epochs: 训练的轮数。在每轮训练中，模型都会进行一次参数更新，直至完成指定的迭代次数。

3. 定义 Sigmoid 函数

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

Sigmoid 函数：这是逻辑回归的核心。它将一个线性输入（w * x + b）转换为一个概率值（在 0 和 1 之间）。Sigmoid 函数公式为：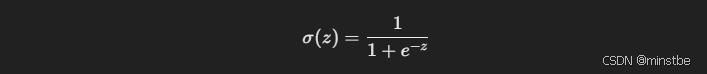
这里 z 就是模型的线性部分 w * x + b。通过这种方式，我们将线性回归的输出映射到概率空间，输出值大于 0.5 时，可以判断为类别 1（大于 5），否则为类别 0（小于等于 5）。

4. 定义模型预测函数

def model(x, w, b):
    return sigmoid(w * x + b)

模型函数：这是模型的前向传播部分，输入 x 通过线性变换（w * x + b）后，传递给 Sigmoid 函数得到一个在 [0, 1] 范围内的值，即模型对该输入属于类别 1 的预测概率。

5. 定义损失函数（交叉熵损失）

def loss_function(y_true, y_pred):
    return -np.mean(y_true * np.log(y_pred) + (1 - y_true) * np.log(1 - y_pred))

交叉熵损失函数：在二分类问题中，交叉熵损失是一个常用的损失函数，它衡量的是模型预测的概率与实际标签之间的差距。公式为：
其中：
- y_true 是真实标签（0 或 1）。
- y_pred 是模型的预测概率（通过 Sigmoid 函数得到）。
- 损失值越小，说明模型的预测与实际标签越接近。

6. 训练模型（梯度下降）

for epoch in range(epochs):
    predictions = model(train_data, w, b)
    loss = loss_function(labels, predictions)
    
    d_w = -np.mean((labels - predictions) * train_data)
    d_b = -np.mean(labels - predictions)
    
    w -= learning_rate * d_w
    b -= learning_rate * d_b
    
    if epoch % 100 == 0:
        print(f"Epoch {epoch}, Loss: {loss}")

训练过程：这是模型训练的核心部分。我们使用 梯度下降法 来优化模型参数 w 和 b，使得模型的损失函数（交叉熵损失）最小化。

具体步骤：
1. 计算预测值： 我们用当前的 w 和 b 计算模型对每个输入的预测值（即 predictions = model(train_data, w, b)）。
2. 计算损失： 使用交叉熵损失函数计算当前模型的误差（即 loss = loss_function(labels, predictions)）。
3. 计算梯度： 使用反向传播算法计算损失函数关于 w 和 b 的梯度。这是通过求损失函数对 w 和 b 的偏导数来完成的：
  - 梯度对于 w（d_w）：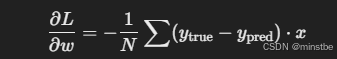
  - 梯度对于 b（d_b）：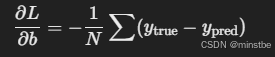
  这些梯度告诉我们，应该如何调整 w 和 b 来减小损失。
4. 更新参数： 根据计算出的梯度，我们用学习率来更新 w 和 b，通过公式：
  - w -= learning_rate * d_w
  - b -= learning_rate * d_b
5. 输出损失值： 每训练 100 轮，就输出一次当前的损失值。

7. 预测新数据

def predict(x):
    return 1 if model(x, w, b) > 0.5 else 0

预测函数： 这个函数通过计算输入 x 对应的概率（通过 Sigmoid 函数），然后使用一个阈值（0.5）将概率转化为类别：
- 如果模型的输出大于 0.5，则预测为 1（大于 5）。
- 如果模型的输出小于或等于 0.5，则预测为 0（小于等于 5）。

8. 预测训练数据和新数据

# 预测训练数据
for i in range(len(train_data)):
    prediction = predict(train_data[i])
    print(f"输入：{train_data[i]}, 预测结果：{prediction}, 真实标签：{labels[i]}")

# 预测新数据
new_data = [4, 6, 8]
for num in new_data:
    result = predict(num)
    print(f"数字 {num} 是否大于 5: {'是' if result == 1 else '否'}")

预测训练数据： 通过调用 predict() 函数，对训练数据进行预测，查看模型的预测值与实际标签的比较。
预测新数据： 在训练结束后，我们还可以使用训练好的模型来对新的数据进行预测（例如数字 4、6 和 8），判断这些数字是否大于 5。

归纳一下：

Sigmoid 函数 将线性回归的输出转换为概率值，适合于二分类任务。
交叉熵损失函数 衡量模型输出与真实标签之间的差距。
梯度下降法 用来优化模型参数，最小化损失函数。
预测函数 将 Sigmoid 输出的概率值转换为 0 或 1，来判断数字是否大于 5。

通过这些步骤，模型在训练过程中会不断调整参数，逐步学习如何从数据中判断数字是否大于 5。

以下是整个过程的完整代码，复制后可直接运行：

import json
import numpy as np

# Sigmoid 函数
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

# 预测函数：根据权重和偏置进行预测
def predict(x):
    return 1 if sigmoid(w * x + b) >= 0.5 else 0

# 训练数据
train_data = np.array([1, 2, 3, 4, 5, 6, 7, 8])
labels = np.array([0, 0, 0, 0, 0, 1, 1, 1])  # 0表示<=5, 1表示>5

# 初始化权重和偏置
w = 0
b = 0

# 学习率和训练轮数
learning_rate = 0.1
epochs = 1000

# 损失函数：交叉熵
def cross_entropy_loss(predictions, labels):
    return -np.mean(labels * np.log(predictions) + (1 - labels) * np.log(1 - predictions))

# 训练模型
def train():
    global w, b
    for epoch in range(epochs):
        total_loss = 0
        # 训练过程：遍历每个训练数据
        for i in range(len(train_data)):
            # 计算预测值
            prediction = sigmoid(w * train_data[i] + b)
            # 计算损失
            total_loss += cross_entropy_loss(prediction, labels[i])
            # 计算梯度
            d_w = (prediction - labels[i]) * train_data[i]
            d_b = (prediction - labels[i])
            # 更新权重和偏置
            w -= learning_rate * d_w
            b -= learning_rate * d_b
        # 打印损失（每 100 轮打印一次）
        if epoch % 100 == 0:
            print(f"Epoch {epoch}, Loss: {total_loss / len(train_data)}")

# 保存模型到文件
def save_model():
    model_params = {'w': w, 'b': b}
    with open('model.json', 'w') as f:
        json.dump(model_params, f)

# 加载已保存的模型
def load_model():
    global w, b
    try:
        with open('model.json', 'r') as f:
            model_params = json.load(f)
            w = model_params['w']
            b = model_params['b']
            print("模型加载成功！")
    except FileNotFoundError:
        print("没有找到模型文件，开始新的训练。")

# 主函数
def main():
    load_model()  # 尝试加载模型
    train()  # 训练模型
    save_model()  # 保存模型
    print("训练完毕，模型保存成功。")

    # 预测训练数据
    print("\n预测训练数据：")
    for i in range(len(train_data)):
        prediction = predict(train_data[i])
        print(f"输入：{train_data[i]}, 预测结果：{prediction}, 真实标签：{labels[i]}")

    # 预测新数据
    new_data = [4, 6, 8]
    print("\n预测新数据：")
    for num in new_data:
        result = predict(num)
        print(f"数字 {num} 是否大于 5: {'是' if result == 1 else '否'}")

if __name__ == "__main__":
    main()

运行结果：