在之前一篇文章中我讲了判断2015年中每一天是星期几的方法
这不禁让我思考如果不限定年份,如何判断每一天是星期几呢?
首先我们明确一下总的判断方法:
公元元年1月1日至指定日期的总天数%7
余数为几就是星期几
难点:求公元元年1月1日至指定日期的总天数
这里默认公元元年1月1日为星期1,文章后面有详细讲为什么
考虑到年、月、日三个变量,发现求总天数应当是分为三个部分的
- 公元元年1月1日至指定年份前一年的总天数
- 指定年份1月1日至指定月份前一月的总天数
- 指定月份1日至指定日的总天数
然后发现求公元元年1月1日至指定年份前一年的总天数不能直接用“年数*365”,还要考虑到平年、闰年的问题,则第一个部分再细分为两个小部分
- 平年年数*365
- 闰年年数*366
此时发现需要解决平年数、闰年数的统计问题
我们判断闰年,则平年数就等于指定年份减去闰年数
这里引入润年的概念
地球绕太阳运行的周期为365天5小时48分46秒(合365.24219天),即一回归年(tropical year)。公历的平年只有365天,比回归年短约0.2422天,所余下的时间约为每四年累积一天,故在第四年的2月末加1天,使当年的时间长度变为366天,这一年就是闰年。现行公历中每400年有97个闰年。按照每四年一个闰年计算,平均每年就要多算出0.0078天,这样,每128年就会多算出1天,经过400年就会多算出3天多。因此,每400年中要减少3个闰年。所以公历规定:年份是整百数时,必须是400的倍数才是闰年;不是400的倍数的世纪年,即使是4的倍数也不是闰年。
这就是通常说的:四年一闰,百年不闰,四百年再闰。例如:2000年是闰年,2100年则是平年。
也就是:能被4整除但不能被100整除或能被400整除的年份为润年
知道了闰年的判断方法,则统计闰年数十分简单,定义变量i,让i从1循环至指定年份前一年,每次循环判断i是否为闰年,如果是则润年数加1(初始值为0)
至此第一部分解决
第二部分,指定年份1月1日至指定月份前一月的总天数
定义数组,将每个月份的天数存进去,定义变量i,让i从1循环到指定月份的前一个月,每次循环每个月的天数加到总天数中(循环前总天数为公元元年1月1日至指定年份前一年的总天数)
至此第二部分解决
第三部分,发现不需要算,指定几就是几。
最后直接算就好
#include <stdio.h>
int main()
{
int year, month, day, sumday, result;
while (1)
{
int sumleapyear = 0;
printf("请输入年:");
scanf_s("%d", &year);
//统计公元元年至去年中有多少个闰年
for (int i = 1; i <= year - 1; i++)
{
if (i % 4 == 0 && i % 100 != 0 || i % 400 == 0)
sumleapyear++;
}
//统计公元元年1月1日至去年12月31日共有多少天
//公元元年至去年中的平年数*365+闰年数*366
sumday = (year - 1 - sumleapyear) * 365 + sumleapyear * 366;
int February;
if (year % 4 == 0 && year % 100 != 0 || year % 400 == 0)
February = 29;
else
February = 28;
int a[13] = { 0,31,February,31,30,31,30,31,31,30,31,30,31 };
printf("请输入月:");
scanf_s("%d", &month);
//统计公元元年1月1日至去年12月31日总天数+今年1月1日至今年上一个月最后一天的总天数
for (int i = 1; i <= month - 1; i++)
sumday += a[i];
printf("请输入日:");
scanf_s("%d", &day);
//公元1月1日至今的总天数求余7
result = (sumday + day) % 7;
if (result != 0)
printf("%d年%d月%d日是星期%d\n", year, month, day, result);
else
printf("%d年%d月%d日是星期日\n", year, month, day);
}
return 0;
}这里用的是格里历,格里历默认公元元年1月1日是星期一
但你可能会思考到一个问题,格里历公元元年1月1日真的是星期1吗?
我也思考了,发现星期是公元321年3月7日才提出来的,这里引入星期的概念
星期,又叫周,是一个时间单位,也是制定工作日、休息日的依据。
星期作为时间周期最早起源于巴比伦。世界通行的星期制是罗马皇帝君士坦丁大帝在公元321年3月7日正式确立的。
在中国古代称“七曜”。七曜在中国夏商周时期,是指日、月及五大行星等七个主要星体,是当时天文星象的重要组织成份,后来借用作七天为一周的时间单位,故称“星期”。
那公元321年3月7日是星期1?
用以上代码输入日期计算后还真是


以上代码输入大于1582年的任意年份计算结果与百度、微软、谷歌等日历的计算结果均相同,那为什么1582年前就有所不同了呢?
查阅相关资料发现1582年前使用的是儒略历,1582年10月4日后才改为现在使用的格里历,儒略历因本身不够精确,在漫长的时间长河中最初的微小误差被慢慢放大,公元前45年1月1日至公元1582年10月4日与实际节气已经产生了10天误差,故教皇格里高利十三世颁布了新的历法格里历(并不是他本人制定的新历法,只是由他颁布并传播出去),并将儒略历1582年10月4日星期四的第二天改为格里历1582年10月15日的星期五(直接删除了10天)。
这就解释了为什么以上代码在1582年前的计算结果与各大厂商的日历有所不同,因为以上代码在1582年前的年份依旧是按照格里历的算法进行计算,历法不同算法不同,计算结果自然是错误的,不过这同样证实了以上代码对于格里历的计算是正确无误的,我们直接用以上代码验算一下1582年10月15日是否为星期五即可

算法正确,那么毫无疑问,按照现在的格里历公元元年1月1日是星期一。
那我们怎么计算儒略历呢?
这里引入儒略历和格里历的百度百科。
儒略历
儒略历 (Julian calendar)是由罗马共和国独裁官儒略·凯撒(又译盖乌斯·尤里乌斯·凯撒)采纳埃及亚历山大的数学家兼天文学家索西琴尼的计算后,于公元前45年1月1日起执行的取代旧罗马历法的一种历法。
儒略历中,一年被划分为12个月,大小月交替;四年一闰,平年365日,闰年366日为在当年二月底增加一闰日,年平均长度为365.25日。
格里历
现行西历即格里历,又译国瑞历、额我略历、格列高利历、格里高利历,称西元。是由意大利医生兼哲学家里利乌斯(Aloysius Lilius)改革儒略历制定的历法,由教皇格列高利十三世在1582年颁行。
格里历与儒略历大致一样,但格里历特别规定,除非能被400整除,所有的世纪年(能被100整除)都不设闰日;如此,每四百年,格里历仅有97个闰年,比儒略历减少3个闰年。格里历的历年平均长度为365.2425日,接近平均回归年的365.242199074日,即约每3300年误差一日,也更接近春分点回归年的365.24237日,即约每8000年误差一日;而儒略历的历年为365.25日,约每128年就误差一日。到1582年时,儒略历的春分日(3月21日)与地球公转到春分点的实际时间已相差10天。因此,格里历开始实行时,将儒略历1582年10月4日星期四的次日,改为格里历1582年10月15日星期五,即有10天被删除,但原星期的周期保持不变。
发现儒略历和格里历的区别就在于对闰年的判定上
格里历闰年判定法
四年一闰,百年不闰,四百年再闰。
儒略历闰年判定法
四年一润。
知道了儒略历对于润年的判定方法,只要再知道儒略历公元元年1月1日是星期几就可以正确计算出1582年10月4日前的每一天是星期几
我的方法为假设儒略历的公元元年1月1日也是星期一,再将以上代码润年的判定方法改为儒略历的判定方法,输入1582年10月4日进行计算,看与史料记载的1582年10月4日是星期四相差几天,在将差的这几天按照“多减少加”的原则并入总天数中,但考虑的公元元年1月1日再减会出现复制的情况,把差值并入总天数的原则改为多“加一循环少加”的原则
更改为如下代码后我们再次运行,输入1582年10月4日
#include <stdio.h>
int main()
{
int year, month, day, sumday, result;
while (1)
{
int sumleapyear = 0;
printf("请输入年:");
scanf_s("%d", &year);
//统计公元元年至去年中有多少个闰年
for (int i = 1; i <= year - 1; i++)
{
if (i % 4 == 0 /* && i % 100 != 0 || i % 400 == 0*/)
sumleapyear++;
}
//统计公元元年1月1日至去年12月31日共有多少天
//公元元年至去年中的平年数*365+闰年数*366
sumday = (year - 1 ) * 365 + sumleapyear;
int February;
if (year % 4 == 0 /* && year % 100 != 0 || year % 400 == 0*/)
February = 29;
else
February = 28;
int a[13] = { 0,31,February,31,30,31,30,31,31,30,31,30,31 };
printf("请输入月:");
scanf_s("%d", &month);
//统计公元元年1月1日至去年12月31日总天数+今年1月1日至今年上一个月最后一天的总天数
for (int i = 1; i <= month - 1; i++)
sumday += a[i];
printf("请输入日:");
scanf_s("%d", &day);
//公元1月1日至今的总天数求余7
//printf("%d\n",sumday+day);
result = (sumday + day ) % 7;
if (result != 0)
printf("%d年%d月%d日是星期%d\n", year, month, day, result);
else
printf("%d年%d月%d日是星期日\n", year, month, day);
}
return 0;
}运行结果为

发现比实际天数多了两天,也就是要在计算时将总天数-2,但公元元年1月1日的总天数就为1,减2直接变为负值, 那我们选择+5,为什么+5?周六-2为周四,周六+5也为周四,可看下图推导。
![]()
这里我们默认公元元年是星期一,但是发现比星期一要少两天或者多五天,那么无论如何,儒略历公元元年为星期六。
我们更改以上代码,将总天数+5,再次计算
#include <stdio.h>
int main()
{
int year, month, day, sumday, result;
while (1)
{
int sumleapyear = 0;
printf("请输入年:");
scanf_s("%d", &year);
//统计公元元年至去年中有多少个闰年
for (int i = 1; i <= year - 1; i++)
{
if (i % 4 == 0 /* && i % 100 != 0 || i % 400 == 0*/)
sumleapyear++;
}
//统计公元元年1月1日至去年12月31日共有多少天
//公元元年至去年中的平年数*365+闰年数*366
sumday = (year - 1) * 365 + sumleapyear + 5;
int February;
if (year % 4 == 0 /* && year % 100 != 0 || year % 400 == 0*/)
February = 29;
else
February = 28;
int a[13] = { 0,31,February,31,30,31,30,31,31,30,31,30,31 };
printf("请输入月:");
scanf_s("%d", &month);
//统计公元元年1月1日至去年12月31日总天数+今年1月1日至今年上一个月最后一天的总天数
for (int i = 1; i <= month - 1; i++)
sumday += a[i];
printf("请输入日:");
scanf_s("%d", &day);
//公元1月1日至今的总天数求余7
//printf("%d\n",sumday+day);
result = (sumday + day ) % 7;
if (result != 0)
printf("%d年%d月%d日是星期%d\n", year, month, day, result);
else
printf("%d年%d月%d日是星期日\n", year, month, day);
}
return 0;
}结果如下


儒略历和格里历的计算我们都解决了,我们将二者的代码结合一下,如下
#include <stdio.h>
int main()
{
while (1)
{
int year, month, day, sumday, week, sumleapyear = 0;
printf("请输入年:");
scanf_s("%d", &year);
if (year == 0)
break;
//统计公元元年至去年中有多少个闰年
if (year > 1582)//通过年份判断将公历和儒略历分开
{
for (int i = 1; i <= year - 1; i++)
{
if (i % 4 == 0 && i % 100 != 0 || i % 400 == 0)
sumleapyear++;
}
}
else
{
for (int i = 1; i <= year - 1; i++)
{
if (i % 4 == 0)
sumleapyear++;
}
sumleapyear += 5;//1582年的儒略历中公元元年不是星期一,为星期六,比周一多五天故加五
//将算法改为儒略历算法发现星期比正确天数多了两天,也就是按元年元日为周一算多两天,往前两天,得儒略历元年元日为周六
//但是往前减二的话会导致元年元月的日期计算出错,故我们往前加五
//算法改为儒略历计算1582年10月4日得星期六,而正确日期为星期四,故多了两天
}
//统计公元元年至去年中有多少个闰年
sumday = (year - 1) * 365 + sumleapyear;
//统计公元元年1月1日至指定年份12月31日共有多少天,公元元年至指定年份年数*365+闰年数
//printf("%d ",sumday);用于临时验证天数准确性
int February;
if (year > 1582)//通过年份判断将公历和儒略历分开
{
if (year % 4 == 0 && year % 100 != 0 || year % 400 == 0)
February = 29;
else
February = 28;
}
else
{
if (year % 4 == 0)
February = 29;
else
February = 28;
}
//区分润年及平年2月的天数
int a[13] = { 0,31,February,31,30,31,30,31,31,30,31,30,31 };
printf("请输入月:");
scanf_s("%d", &month);
if (month == 0)
break;
//统计公元元年1月1日至去年12月31日总天数+今年1月1日至今年上一个月最后一天的总天数
for (int i = 1; i <= month - 1; i++)
sumday += a[i];
if (year == 1582 && month == 11 || year == 1582 && month == 12)
sumday += 11;//这里为何不加10?
printf("请输入日:");
scanf_s("%d", &day);
if (day == 0)
break;
if (year == 1582 && month == 10 && day > 4 && day < 15)
{
printf("历法变更,不存在这一天!\n\n");
//_sleep(1000);
continue;
}
//公元1月1日至今的总天数求余7
if (year == 1582 && month == 10 && day >= 15)
week = (sumday + day - 10) % 7;//历法变更删除10天
else
week = (sumday + day) % 7;
if (week != 0)
printf("%d年%d月%d日是星期%d\n\n", year, month, day, week);
else
printf("%d年%d月%d日是星期日\n\n", year, month, day);
}
return 0;
}运行结果如下

至此,我们解决了公元年每天一是星期几的计算。
我正在写一个系列的项目“从零开始的万年历”,上一篇文章讲了2015年中每一天是星期几的计算方法,有兴趣的铁子可以看一下。
下一篇文章我们讲如何实现一个简单的万年历。
最后感概一下,还是我们中国的农历牛逼啊!太顶了!
其实在写的时候我就想到整个运算过程是有一定规律的,或许可以推导出一个通用公式来,在写完之后我去查了有关资料,发现真的有两个通用公式,基姆拉尔森计算公式和蔡勒公式。
基姆拉尔森计算公式
本公式用来计算指定的年月日是星期几
算法如下:
基姆拉尔森计算公式 (C++与VB.Net整数除法和取余运算符不同)
W= (d+2*m+3*(m+1)/5+y+y/4-y/100+y/400+1)%7 //C++计算公式
W = (D + 2 * M + 3 * (M + 1) \ 5 + Y + Y \ 4 - Y \ 100 + Y \ 400+1) Mod 7 'VB.Net计算公式
在公式中d表示日期中的日数,m表示月份数,y表示年数。
w表示星期,w的取值范围是0~6,0代表星期日,1~6星期一到星期六。
注意:在公式中有个与其他公式不同的地方:
C实现
#include
void main() {
int y=2013,m=1,d=1;
int w;
char *weekday[7]= {
"Sunday","Monday","Tuesday","Wednesday","Thursday","Friday","Saturday"
}
;
if (m==1 || m==2) {
m=(m==1?13:14);
y=y-1;
//此处表示把1,2月计算到上一年的13,14月<修改日期:2014.5.13 by 杨康佳>
}
w=(d+2*m+3*(m+1)/5+y+y/4-y/100+y/400+1)%7;
printf("%s\n",weekday[w]);
}蔡勒公式
或者是:
若要计算的日期是在1582年10月4日或之前,公式则为
以1582年10月4日为例:
1582年10月4日后:w = (d + 1+ 2*m+3*(m+1)/5+y+y/4-y/100+y/400)%7;
1582年10月4日前:w = (d+1+2*m+3*(m+1)/5+y+y/4+5) % 7;
或者1752年9月3日为例
1752年9月3日后:w = (d + 2*m+3*(m+1)/5+y+y/4-y/100+y/400)%7;(这个公式应该是跟正常的相差1的,也就是算出来相差了一天)
1752年9月3日前:w = (d+2*m+3*(m+1)/5+y+y/4+5) % 7;
注:罗马教皇决定在1582年10月4日后使用格利戈里历法;而英国则是在1752年9月3日后才接受使用格利戈里历法。
注意:
当年的1,2月要当成上一年的13,14月进行计算
w:星期; w对7取模得:0-星期日,1-星期一,2-星期二,3-星期三,4-星期四,5-星期五,6-星期六
c:世纪(注:一般情况下,在公式中取值为已经过的世纪数,也就是年份除以一百的结果,而非正在进行的世纪,也就是现在常用的年份除以一百加一;不过如果年份是公元前的年份且非整百数的话,c应该等于所在世纪的编号,如公元前253年,是公元前3世纪,c就等于-3)
y:年(一般情况下是后两位数,如果是公元前的年份且非整百数,y应该等于cMOD100+100)
m:月(m大于等于3,小于等于14,即在蔡勒公式中,某年的1、2月要看作上一年的13、14月来计算,比如2003年1月1日要看作2002年的13月1日来计算)
d:日
[ ]代表取整,即只要整数部分。
下面以中华人民共和国成立100周年纪念日那天(2049年10月1日)来计算是星期几,过程如下:
w=y+[y/4]+[c/4]-2c+[26(m+1)/10]+d-1
=49+[49/4]+[20/4]-2×20+[26×(10+1)/10]+1-1
=49+[12.25]+5-40+[28.6]
=49+12+5-40+28
=54 (除以7余5)
即2049年10月1日(100周年国庆)是星期五。
再比如计算2006年4月4日,过程如下:
w=y+[y/4]+[c/4]-2c+[26(m+1)/10]+d-1
=6+[6/4]+[20/4]-2*20+[26*(4+1)/10]+4-1
=-12 (除以7余5,注意对负数的取模运算!实际上应该是星期二而不是星期五)
w=(-12%7+7)%7=2;
C实现
#include<stdio.h>
int main()
{
int year, month, day;
while (scanf("%d %d %d", &year, &month, &day) != EOF)
{
if (month == 1 || month == 2)//判断month是否为1或2
year--, month += 12;
int c = year / 100;
int y = year - c * 100;
int week = y + y / 4 + c / 4 - 2 * c + 26 * (month + 1) / 10 + day - 1;
while (week < 0)
week += 7;
week %= 7;
switch (week)
{
case 1:printf("Monday\n"); break;
case 2:printf("Tuesday\n"); break;
case 3:printf("Wednesday\n"); break;
case 4:printf("Thursday\n"); break;
case 5:printf("Friday\n"); break;
case 6:printf("Saturday\n"); break;
case 0:printf("Sunday\n"); break;
}
}
return 0;
}







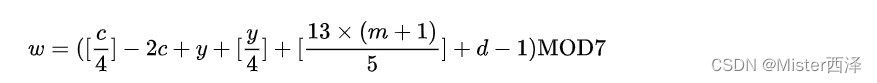
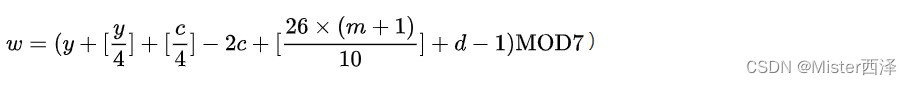

















 1690
1690

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








