解密分类模型的核心：Sigmoid与SoftMax的应用与奥秘

其实目标检测也用到了，毕竟检测包括定位与分类嘛。

一、Sigmoid

Sigmoid针对多标签分类问题 = 答案可共存（如生病和住院）
$$Sigmoid(x)=\frac{1}{1+e^{-x}}$$

输入得分值，输出概率值

---

二、SoftMax

针对多类别分类问题 = 答案唯一（如图像分类猫狗）

它会将每个类别的得分换算成概率。
$$SoftMax(x)=\frac{e^{x_i}}{{\sum }_{j=1}^n{e}^{x_j}}$$

输入得分值，输出概率值

• 分子是类别 $i$ 的得分；
• 分母是所有类别的得分和；
• softmax的输入是得分，输出是概率，且所有类别的概率和为1；

且所有类别概率之和为1：
$$\frac{e^{x_1}+...+e^{x_n}}{{\sum }_{j=1}^n{e}^{x_j}}=1$$

---

三、分类任务中为啥要使用SoftMax

原因一：分类任务中，神经网络最终要选择概率最高的类别作为自己的分类结果。需要一个方法将得分换算成概率。

原因二：分类任务中，容易出现得分相近的情况，如果相近的得分换算出相近的概率，这就不利于反向传播与模型的迭代。而指数 $e^x$ 能让得分大的类别换算的概率更大，让得分小的类别换算的概率更小。

• 举个栗子：一张图片猫2分狗1.9分，$e^{1.9}=6.7，e^2=7.4$。

指数曲线如下图所示：

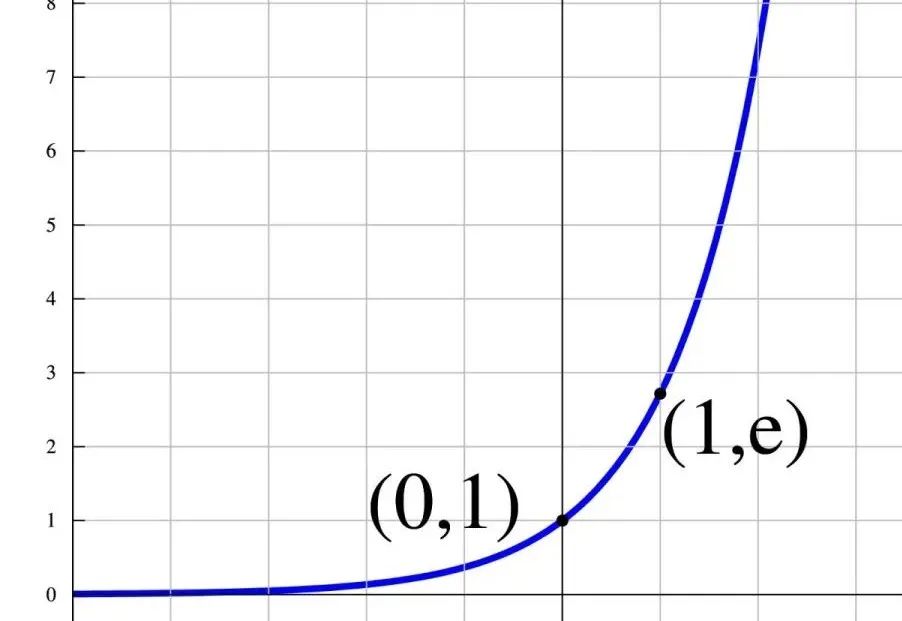
注：本图片来自图片来源

---

四、帮助记忆

SoftMax是软Max，那么有HardMax吗？就算平时用的$Max(3,4)=4$

到底咯，如果这篇文章对您有些许帮助，请帮忙点个赞👍或收个藏📃。您的支持是我继续创作的动力💪！

---

不要害怕，不要着急。保持每日的前进☀️与积极的内心❤️，命运总在曲折中馈赠最好的礼物。