树型结构及其应用场景

一、二叉树

    1、完全二叉树：除了叶子层，其它层的节点都是满的，且节点按从左至由分布

     2、满二叉树：除了叶子节点，每个节点都有左右子节点

     3、平衡二叉树（重要）：空树或者任意一个节点的左子树和右子树的高度差不超过1

     4、排序二叉树：左节点的值少于根节点，右节点的值大于根节点，时间复杂度为log2n

二、B-tree

      B树是一棵多路平衡二叉树，可以当作索引的存储结构，在理解它之前，我们先看一下它的演化过程。

      当我们想实现一个索引的功能的时候，最先想到的是排序二叉树，因为跟二分查找法一样，时间效率是比较高的，是比较理想的存储结构；但它有个缺点，就是非常不稳定，查找一个值，最好的情况就是在根节点就找到了，只需比较一次即可，最坏的情况就是要找到最后一个节点才能找到，最坏情况比较了多少次呢？取决于这棵树的层数，层数越高，比较的次数越多，极端情况下，二叉树可能都只有左子节点或者只有右子节点，那么有n个节点，就有n层，比较次数为n，可以想见，非常的不稳定。

      一般在项目中，我们宁愿牺牲点性能，查询慢一点，但希望它能稳定;假如同样多的节点，要降低比较次数，就要降低层数，所以二叉树又矮又胖是我们最喜欢的，刚巧平衡二叉树满足我们，所以我们把索引的存储结构设计为平衡的排序二叉树。

      经过调整之后我们发现确实稳定了，但出现了新的问题。我们数据库大都是直接存文件的，查询一条数据每次都得访问一次磁盘，大家知道访问磁盘相对访问内存是比较慢的，它里面有寻找磁道、io等操作上的消耗，这样一来瓶颈出现在了io上，总体上还是不尽如人意，那怎么办呢？

      其实操作系统本身就已经遇到过这种问题，而且它们已经给出了解决方案，操作系统是这样做的：读取磁盘上一个地址上的数据的时候，会把它周围的数据也一块读出来，读多少取决于不同操作系统的设计，一般来说是4k或者8k,这些数据称为一页；所以我们完全可以利用这个规则，把多个节点的数据存储在连续磁盘地址上面，这样只需一次io就可以取出很多数据了，所以就把二叉树的节点由存一个值改为存多个值，每两个值之间都会有一棵子树，存的时候这个节点的所有值一起存，取的时候也一起取，即解决了io操作过多导致的查询效率低下的问题；最终形成的这棵树即是B-tree。

     以上是B-tree的优化过程，从中可以知道B树的几个特性：

      1、多路、有序、平衡。多路和有序不用多说，平衡是如何做到的，这个是在构建树的时候，加入一个节点，如果达到了节点最大值数量，则向上分裂，从而保证整棵树的平衡，至于具体的分裂过程，网上有很多资料，这里只是加强理解及应对面试，就不细说了。

      2、查找的时间复杂度少于排序二叉树，因为当我们确定一个值在某个节点之后，还需遍历这个节点的所有关键字，才能找到数据，所有时间复杂度应该是log2n + m,这个m为节点数量

      3、B树的适用场景，它解决的是读取磁盘的问题，自然适用的类似数据库一样数据量大、磁盘io多的场景，如果都是在内存中操作的话，后面说的红黑树比它更合适；目前使用B树作为索引存储结构的有mongodb，postgres，oracle，sqlserver

三、B+tree

       b树已经很好了，但仔细想想，它还不是最完美的解决方案，为什么呢？主要还有以下几个缺点：

       1、还不够稳定；当树形成之后在不修改的前提下，我们希望有一个固定的比较次数，显然b树做不到。

       2、一个节点存储的关键字还不够多，io操作还是没有降到我们理想的情况。

       3、对于按顺序取一段数据并不方便。

       对于这些问题，我们看看b+tree怎么去解决的。

       B+tree节点只存储关键字（包含父节点的关键字），不存储数据，而是把数据放到叶子节点，这样有几个好处，一是非叶子节点放的关键字更多的，也意味着磁盘读取一页数据里面包含的信息是更多的，二是想要取得数据，就得从根节点一直访问到叶子节点，这样基本上查询任何关键字比较次数是一致的，这样就解决了1和2的问题。

      B+tree除了把数据放到叶子节点外，还做了一件事，因为叶子节点包含了所有的关键字和数据，且从左到右是有序的，所以每个叶子节点还额外的保存了它的左右页子节点的指针，所以在叶子节点层形成了一个双向链表，这对于按顺序取一段数据是非常方便的，取需要查询开头或者结尾的关键字，就可以向左或者向右按顺序查出想要的一段数据。

      由于这些改动，B+tree和B-tree的查询效率很难说谁高谁低，这得看关键字的规模（因为B+tree虽然增加了比较次数及节点遍历的长度，但节省了io），但更稳定，这是我们需要的，而且在因为叶子层的链表结构，有时候更好用。

      通过B+tree实现数据库有 mysql(innerdb)

四、23树

       这里提到23树，是因为红黑树是23树演变而来，23树如下图所示，由2节点（有两棵子树）和3节点（有三棵子树）组成

      

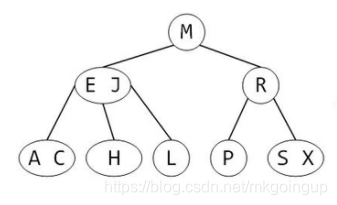
     23树在构建的时候如果超过了节点关键字数量的限制，会通过冒泡的方式向上融合（具体的构建方式可以百度，有详细的过程），以保证这棵树的完美平衡，所有节点到它的所有的叶子节点的距离是相同的。

     但这种方式表示的树代码实现的时候比较麻烦，需要标记每个节点是2节点还是3节点，然后判断有几个子树，比较复杂，有人就想把它拆成一棵二叉树来实现，如下

3节点两个关键字用红连接线表示，并且我们再约定，红连接节线左边的节点为红节点，右边的节点为黑节点，树其它的节点都为黑节点，那么它就演变成了一棵红黑树。

五、红黑树

   由23树演变而来的一棵二叉树，节点类型有红节点和黑节点，因为红黑节点是了3节点演变来的，因此它继承了23树 节点到它的所有叶子节点的距离相同 的特性：红黑树所有节点到它的叶子节点经过的黑球的数量是相同的。个人觉得理解了23树后不需要去记这个定义。

   红黑树保证平衡的操作是自旋转，在构建的时候加入了一个节点后会检查父节点为根节点的这棵子树是否平衡，不平衡就要选择一个节点进行旋转来维持平衡，旋转的时候有规则，左右子树节点会相应的移动，具体过程还是百度。

   红黑树对于只有少量数据，放在内存中操作业务场景来说是比较完美的数据结构，即稳定，同时查询效率也高，跟二分查找一样的，但它不适用于有大量io的场景，如数据库索引。

   java 中 TreeMap 和 TreeSet 是通过红黑树实现的，但这两种结构使用得很少。

 

六、Hash树

     这个从来没见有人问过，可作为兴趣了解。

     hash树首先它不是一个二叉树，它的路数也是不固定的，取决于存储的关键字的值，是在不断变化的。

     它的原理依据是质数分辩定理，即一个整数一定是可以分解为多个质数相乘，所以把关键字按2、3、5、7...一个一个模运算，余数就是数据存储的路径，如果冲突，就对下一个质数进行模运算，直到找到一个不冲突的位置，放一张网上找的图：

这种树的特点是无序，它是一棵无序树，但查找效率很高，不适合有顺序要求的场景。

目前了解到有使用的案例是 区块链技术中的Merkle树，用来查找区块信息

 

以上是树型结构的总结，主要列出思路、优缺点及应用场景，每种结构详细的过程还需网上自行搜索，仅供参考，如果有误，欢迎指正