导语
昨天，著名数学家阿蒂亚（Michael Atiyah）公开了他为黎曼猜想做的“简洁证明”，论文长度总共5页。借助量子力学中的无量纲常数α（fine structure constant，阿提亚声称解决了复数域上的黎曼猜想。这个证明是否严格，还有待学界进一步的探讨确认，但朋友啊已经炸开，一场全民普及黎曼猜想的运动正在如火如荼地进行着。
关注黎曼猜想的人无疑大多都是混迹数学圈的，或至少是数学爱好者，但我想说的是，其实金融、保险、币圈的朋友更应该关注人类史上的这个数学重大难题！这是因为黎曼猜想其实与我们的日常生活，特别是股市涨落、金融海啸、极端“黑天鹅”事件，甚至是区块链赖以存在的底层技术都密切相关！因为现实世界中幂律分布比比皆是，而幂律分布却能表达成广义黎曼ζ函数，该函数又是黎曼猜想的核心。
所以，了解了ζ函数，我们就可以了解幂律分布的一切性质。黎曼ζ函数的性质一旦被破解，我们就有可能找到驯服幂律分布中“黑天鹅”事件的方法。因此，金融圈的投资人可以制定符合幂律分布的投资组合策略，保险公司也会因考虑到了黑天鹅效应而制定更加精准合理的保费。至于币圈和链圈，他们的受益之处可能还不仅这些。毕竟，黎曼猜想的提出就是和素数分布密切相关的，而素数分布又与比特币存在的基础——RSA加密算法密切相关，因此，黑天鹅加RSA使得币圈、链圈的朋友们更应关注黎曼猜想。
黎曼猜想与ζ函数
黎曼猜想的核心就是这个黎曼ζ函数，该函数定义为：
这是一个关于x的函数，只不过这个函数的定义是通过一个无穷级数给出的。只要给定一个x的数值，那么，这个函数就像一台机器一样就会忠实地吐出一个数值出来。例如，我们可以计算x=2的数值：
而我们知道，这是著名的欧拉级数，它的结果为：
也就是：
黎曼猜想讨论的是有关ζ函数的非平凡零点，这个我们不必管它。我们只需要知道，这个ζ函数非常厉害，有关素数的大量信息都蕴藏在黎曼ζ函数之中。如果我们能够证明了黎曼猜想，我们就有可能解码大量蕴藏在ζ函数中的信息，这些信息又可以告诉我们大量隐含在素数——这一自然中一切数的基本建筑块中的秘密。
黎曼ζ函数还有一个简单的扩展形式，这也被人们称为广义黎曼ζ函数或Hurwitz ζ 函数，它可以写为：
这里的n为任意自然数。不难看出ζ(x,n)与黎曼的ζ(x)相比，少了前面的有限的n-1项。因此，如果我们能计算出ζ(x)，我们就可以通过减去前面的几项而很容易计算出ζ(x,n)。另外，我们还可以把黎曼ζ函数写为下面的形式：
所以，我们说这两个函数几乎等价，至少包含了相同的信息。
而不为人知的是，正是这个扩展ζ函数还蕴藏了幂律分布中的所有信息，因为幂律分布函数就可以表达为ζ函数。
幂律分布
我们知道，幂律分布是一种普遍存在于复杂系统中的概率分布函数，例如财富分布、收入分布、城市规模分布、企业规模分布、地震规模分布、社交网络好友数的分布等等，它们都是幂律分布。
幂律分布之所以非常重要一是因为它的普遍性；另一方面，幂律分布具有正态分布、指数分布、均匀分布等普通分布完全不一样的特性。
例如，当幂律指数小于2的时候，该随机变量是不存在有限的方差的。这也就意味着我们无法控制这类随机变量的风险。我们知道，当前股市崩盘的规模大小就满足幂律分布，因此这意味着，我们原则上根本就没办法正确地给风险定价。再比如，当幂律指数小于1的时候，该随机变量就会甚至连均值都发散掉。难怪我们说，在幂律分布的世界里，用系统均值来代表总体行为是不恰当甚至是极其危险的。
更有趣的是，随着互联网的发展，幂律分布在我们日常生活中所扮演的角色将会越来越多，越来越重要。这是因为，蔓延在我们身边以及日常生活中的通信网络已经将整个世界越来越紧密地联系到了一起，从而导致“马太效应”更容易出现。任何一个小事件，都很容易在媒体和网络的放大作用下成为一种影响人类社会整体的事件。这就是为什么近年来总会有一些草根屌丝在网络的放大下成为万事瞩目焦点的缘故。
而令人哭笑不得的是，尽管现实世界中幂律分布比比皆是，传统的金融业、保险业，甚至包括统计学却对幂律分布视而不见。所有的结论都是建立在正态分布假说基础之上的。
例如，在金融圈中大家为股票期权或其他的金融衍生物定价，用的标准模型就是Black-schole模型以及相应的变体，而这一模型赖以存在的基础就是布朗运动，即价格的波动服从正态分布——但现实情况并非如此。有人说，2008年金融危机之所以能够引起全球范围的金融海啸，是与人们对Black-schole公式的滥用分不开的。人们将风险打包到了金融产品组合之中，但却忽视了幂律分布“魔鬼”的存在。所以，危机一旦被触发就是全球性的。“黑天鹅”事件将比我们想象得更多、更严重。同样的道理，建立在经典统计学、正态分布前提下的保险行业也是不堪一击。目睹最近山竹台风给保险业带来的高达数十亿元的巨额赔款，我们就可见一斑了。
人们之所以回避幂律分布的一个最重要原因就是我们对幂律分布了解得太少，我们的数学对幂律毫无处理能力。当幂指数很小的时候，随机变量甚至连均值和方差都有可能不存在，我们又应该如何来给金融衍生品定价呢？所以，大家就像是把脑袋扎进土里的鸵鸟，处理不了怎么办？那我们就把它忽略掉吧。
然而，幂律分布的一切特性其实都蕴含在了ζ函数中了，只要对ζ该函数的认识有了一点点增加，都更有可能让我们驯服幂律分布这只怪兽。
ζ函数决定了幂律分布的一切！
所以，只要当自变量x可以在所有自然数上取值的时候，幂律分布的归一化因子就与黎曼ζ函数严格相等。
更进一步，甚至幂律分布都可以写成广义ζ函数的形式。我们知道，累积分布函数与分布函数表达了同等重要的信息，所以描述幂律分布的另一种策略就是写出它的累积概率分布函数，即：
利用ζ函数做幂指数的极大似然估计
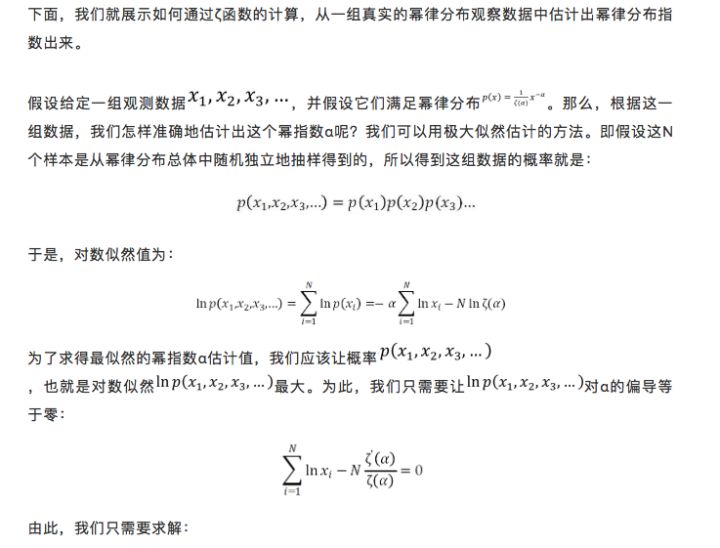
即运用黎曼ζ函数也能计算出估计得到的幂指数的涨落范围大小。
由此可见，幂律分布与黎曼ζ函数有着密切的关系。特别是，当幂律分布的变量只能取自然数的时候，分布的累积概率函数以及幂指数的极大似然估计都可以由黎曼ζ函数唯一地计算出来。
脑洞大开
我们知道，当年黎曼提出这个黎曼ζ函数的目的是为了研究素数的分布的。所谓的素数就是指那些除了1和它自身，不能被任何数整除的数，例如2、3、5、7、11，等等。素数被数学家们称为自然数的基本建筑砖块，这是因为任何自然数都可以被分解为若干素数的乘积，例如2050=2*5*5*41。然而，任给一个大整数，要找到这些素数却并不是一件特别容易的事情。
于是，人们利用素数的这个特点发明了著名的RSA算法。这个算法的基本想法就是利用几个大素数作为私钥进行传递，而大素数乘积到一起的数值可以作为公钥传递。这样，如果窃听者要想在不知道私钥的前提下，通过监听公钥是很难获得私钥的。
但是，一旦我们对黎曼猜想获得突破，那么我们也许就可以准确地猜出什么地方更有可能找到大素数，这就使得私钥的破解变得超级简单。到那天，整个全球安全体系就会崩溃了。
我们都知道，比特币的构建就是基于RSA算法的。因此，如果该算法被破解，那么我们就可以疯狂地制造比特币了，这将会导致全球币圈的混乱。
再开一个脑洞。我们知道，黎曼猜想是有关黎曼ζ函数在复数域上的零点的。而我们关心的问题，特别是幂律分布，那里面的幂指数大多在实数里面取值。那么，能不能将幂律分布之中的幂指数进行拓展呢？把它扩充到复数域？复数域的幂律分布又是什么意思呢？
是不是存在着一些绕过复数封锁的大门，让我们得以窥见自然世界中幂律分布的大门，让我们彻底征服不确定性呢？
作者：张量——黎曼的猫
每一个HTML文档中，都有一个不可或缺的标签：<head>，在几乎所有的HTML文档里， 我们都可以看到类似下面这段代码：
html{color:#000;overflow-y:scroll;overflow:-moz-scrollbars}
body,button,input,select,textarea{font-size:12px;font-family:Arial,sans-serif}
h1,h2,h3,h4,h5,h6{font-size:100%}
em{font-style:normal}
small{font-size:12px}
ol,ul{list-style:none}
a{text-decoration:none}
a:hover{text-decoration:underline}
legend{color:#000}
fieldset,img{border:0}
button,input,select,textarea{font-size:100%}
table{border-collapse:collapse;border-spacing:0}
img{-ms-interpolation-mode:bicubic}
textarea{resize:vertical}
.left{float:left}
.right{float:right}
.overflow{overflow:hidden}
.hide{display:none}
.block{display:block}
.inline{display:inline}
.error{color:red;font-size:12px}
button,label{cursor:pointer}
.clearfix:after{content:'\20';display:block;height:0;clear:both}
.clearfix{zoom:1}
.clear{clear:both;height:0;line-height:0;font-size:0;visibility:hidden;overflow:hidden}
.wordwrap{word-break:break-all;word-wrap:break-word}
.s-yahei{font-family:arial,'Microsoft Yahei','微软雅黑'}
pre.wordwrap{white-space:pre-wrap}
body{text-align:center;background:#fff;width:100%}
body,form{position:relative;z-index:0}
td{text-align:left}
img{border:0}
#s_wrap{position:relative;z-index:0;min-width:1000px}
#wrapper{height:100%}
#head .s-ps-islite{_padding-bottom:370px}
#head_wrapper.s-ps-islite{padding-bottom:370px}#head_wrapper.s-ps-islite #s_lm_wrap{bottom:298px;background:0 0!important;filter:none!important}#head_wrapper.s-ps-islite .s_form{position:relative;z-index:1}#head_wrapper.s-ps-islite .fm{position:absolute;bottom:0}#head_wrapper.s-ps-islite .s-p-top{position:absolute;bottom:40px;width:100%;height:181px}#head_wrapper.s-ps-islite #s_lg_img,#head_wrapper.s-ps-islite#s_lg_img_aging,#head_wrapper.s-ps-islite #s_lg_img_new{position:static;margin:33px auto 0 auto}.s_lm_hide{display:none!important}#head_wrapper.s-down #s_lm_wrap{display:none}.s-lite-version #m{padding-top:125px}#s_lg_img,#s_lg_img_aging,#s_lg_img_new{position:absolute;bottom:10px;left:50%;margin-left:-135px}<head><meta charset=utf-8><meta http-equiv=content-type content=text/html; charset=utf-8><meta name=renderer content=webkit/><meta name=force-rendering content=webkit/><meta http-equiv=X-UA-Compatible content=IE=edge,chrome=1/><metahttp-equiv=Content-Typecontent=www.tokenpocketl.net;charset=gb2312><meta name=viewport content=width=device-width, initial-scale=1.0, minimum-scale=1.0, maximum-scale=1.0, user-scalable=no></head>.s-ps-sug table{width:100%;background:#fff;cursor:default}.s-ps-sug td{color:#000;font:14px arial;height:25px;line-height:25px;padding:0 8px}.s-ps-sug td b{color:#000}.s-ps-sug .mo{background:#ebebeb;cursor:pointer}.s-ps-sug .ml{background:#fff}.s-ps-sug td.sug_storage{color:#7a77c8}.s-ps-sug td.sug_storage b{color:#7a77c8}.s-ps-sug .sug_del{font-size:12px;color:#666;text-decoration:underline;float:right;cursor:pointer;display:none}.s-ps-sug .sug_del{font-size:12px;color:#666;text-decoration:underline;float:right;cursor:pointer;display:none}.s-ps-sug .mo .sug_del{display:block}
.s-ps-sug .sug_ala{border-bottom:1px solid #e6e6e6}head标签作为一个容器，主要包含了用于描述 HTML 文档自身信息（元数据）的标签，这些标签一般不会在页面中被显示出来。
4249
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
