版权声明:本文为博主原创文章,未经博主允许不得转载。
1.前言
之前我们讨论的PCA、ICA也好,对样本数据来言,可以是没有类别标签y的。回想我们做回归时,如果特征太多,那么会产生不相关特征引入、过度拟合等问题。我们可以使用PCA来降维,但PCA没有将类别标签考虑进去,属于无监督的。
再举一个例子,假设我们对一张100*100像素的图片做人脸识别,每个像素是一个特征,那么会有10000个特征,而对应的类别标签y仅仅是0/1值,1代表是人脸。这么多特征不仅训练复杂,而且不必要特征对结果会带来不可预知的影响,但我们想得到降维后的一些最佳特征(与y关系最密切的),怎么办呢?
2.二类LDA的数学原理
2.1 问题的引入
首先利用Logistic回归作铺垫。给定m个n维特征的训练样例x(i)={ x(i,1), x(i,2),...,x(i,n)};其中,i=1~m。每个数据集x(i),都会对应一个类标签y(i)。我们就是要学习出参数θ,使得下式满足:
y(i) = g(θ)x(i),其中,g是sigmoid函数
现在,我们只考虑最简单的二值分类问题,也就是说只有y=0和y=1两种情况:
为了方便表示,我们对符号进行重新定义,给定特征为d维的N个样例,x(i)={ x(i,1), x(i,2),...,x(i,n)},其中有N1个样例属于类别w1
,另外
N2个样例属于类别
w2。
现在我们觉得原始特征数太多,想将d维特征降到只有一维,而又要保证类别能够“清晰”地反映在低维数据上,也就是这一维就能决定每个样例的类别。我们将这个最佳的向量称为w(d维),那么样例x(d维)到w上的投影可以用下式来计算:这里得到的y值不是0/1值,而是x投影到直线上的点到原点的距离。当x是二维的,我们就是要找一条直线(方向为w)来做投影,然后寻找最能使样本点分离的直线。如下
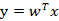
应该注意到,这里得到的y值并不是0/1值,而是x投影到直线上的点到原点的距离。
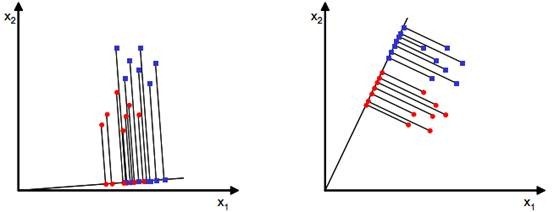
当x是二维特征时,降维后的一维特征应该是一条直线,然后寻找最能使样本点分离的直线。如下图所示:
从直观上来看,右图比较好,可以很好地将不同类别的样本点分离。接下来从定量的角度找到这个最佳的w。
2.2 理论推导
首先我们寻找每类样例的均值(中心点),假设这里i只有两个:
由于x到w投影后的样本点均值为:
由此可知,投影后的的均值也就是样本中心点的投影。
什么是最佳的直线(w)呢?我们首先发现,能够使投影后的两类样本中心点尽量分离的直线是好的直线,定量表示就是:
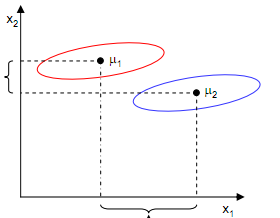
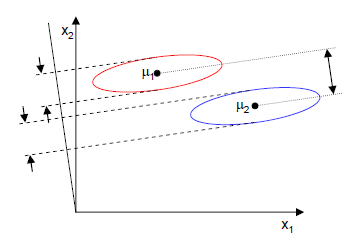
J(w)越大越好。但是只考虑J(w)行不行呢?可定不行的,看下图:
样本点均匀分布在椭圆里,投影到横轴x1上时能够获得更大的中心点间距J(w),但是由于有重叠,x1不能分离样本点。投影到纵轴x2上,虽然J(w)较小,但是能够分离样本点。因此我们还需要考虑样本点之间的方差,方差越大,样本点越难以分离。
我们使用另外一个度量值,称作散列值(scatter),对投影后的类求散列值,如下:
感觉这个东西和方差长得好像就对了~~~散列值的几何意义是样本点的密集程度,值越大,越分散,反之,越集中。而我们想要的投影后的样本点的样子是:不同类别的样本点越分开越好,同类的越聚集越好,也就是均值差越大越好,散列值越小越好。正好,我们可以使用J(w)和S来度量,最终的度量公式是:
接下来的事就比较明显了,我们只需寻找使J(w)最大的w即可。
2.3 如何最优化评判函数J(w)
先把散列值公式展开:
我们定义上式中中间那部分:
很明显,这是一个类内的测度,称为散列矩阵(scatter matrices)。
我们继续定义:Sw = S1+S2。那么Sw就定义为类内散射矩阵。
那么回到上面2.3节最上面的公式,使用Si替换中间部分,得:
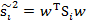
到此,分母已经搞定,我们开始研究分子。
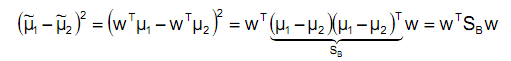
SB称为类间散射矩阵,是两个向量的外积,虽然是个矩阵,但秩为1。
那么J(w)最终可以表示为:
在我们求导之前,需要对分母进行归一化,因为不做归一的话,w扩大任何倍,都成立,我们就无法确定w。因此我们打算令
,那么加入拉格朗日乘子后,求导:
如果SW可逆,那么将求导后的结果两边都乘以SW的逆,得
(λ是largerange参量)
这个可喜的结果就是w就是矩阵
的特征向量了。这个公式称为Fisher linear discrimination。
2.4 其他的发现
对于前面的类间差别公式(between classes)SB:
左右同时乘以一个w:
带入最后的特征值公式有:
由于对w扩大缩小任何倍不影响结果,因此可以约去两边的未知常数λ和λW,得到:
这样,我们完全通过拓扑的方法得到了最终的最优变换矩阵,该矩阵确实与类内方差和类间样本均值相关。所以,我们只需要求出原始样本的均值和方差就可以求出最佳的方向w,这就是Fisher于1936年提出的线性判别分析。
所以,上面的二维投影图采用LDA处理后的结果应为:
对于多类的分析方法与之类似。
3.参看资料
http://www.cnblogs.com/jerrylead/archive/2011/04/21/2024384.html








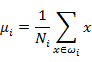
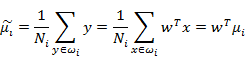
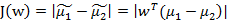
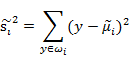
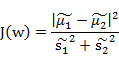
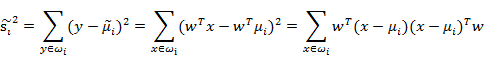
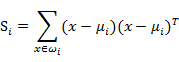
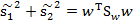
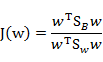
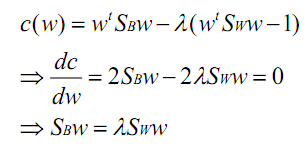
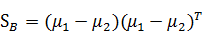
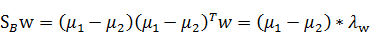
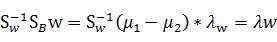
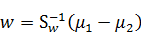














 1522
1522

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








