Poj 3239 Solution to the n Queens Puzzle

1.Link：

http://poj.org/problem?id=3239

2.Content：

Solution to the  n Queens Puzzle

Time Limit: 1000MS		Memory Limit: 131072K
Total Submissions: 3459		Accepted: 1273		Special Judge

Description

The eight queens puzzle is the problem of putting eight chess queens on an 8 × 8 chessboard such that none of them is able to capture any other. The puzzle has been generalized to arbitrary n × n boards. Given n, you are to find a solution to the n queens puzzle.

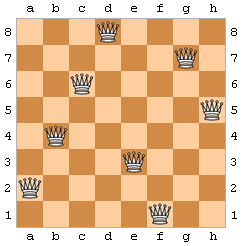
Input

The input contains multiple test cases. Each test case consists of a single integer n between 8 and 300 (inclusive). A zero indicates the end of input.

Output

For each test case, output your solution on one line. The solution is a permutation of {1, 2, …, n}. The number in the ith place means the ith-column queen in placed in the row with that number.

Sample Input

8
0

Sample Output

5 3 1 6 8 2 4 7

Source

POJ Monthly--2007.06.03, Yao, Jinyu

3.Method:

一开始用8皇后的方法，发现算不出来。

只能通过搜索，可以利用构造法，自己也想不出来构造，所以直接套用了别人的构造公式

感觉没啥意义，直接就用别人的代码提交了，也算是完成一道题目了

构造方法：

http://www.cnblogs.com/rainydays/archive/2011/07/12/2104336.html

一、当n mod 6 != 2 且 n mod 6 != 3时，有一个解为：
2,4,6,8,...,n,1,3,5,7,...,n-1        (n为偶数)
2,4,6,8,...,n-1,1,3,5,7,...,n        (n为奇数)
(上面序列第i个数为ai,表示在第i行ai列放一个皇后;...省略的序列中,相邻两数以2递增。下同)
二、当n mod 6 == 2 或 n mod 6 == 3时，
(当n为偶数,k=n/2；当n为奇数,k=(n-1)/2)
k,k+2,k+4,...,n,2,4,...,k-2,k+3,k+5,...,n-1,1,3,5,...,k+1        (k为偶数,n为偶数)
k,k+2,k+4,...,n-1,2,4,...,k-2,k+3,k+5,...,n-2,1,3,5,...,k+1,n    (k为偶数,n为奇数)
k,k+2,k+4,...,n-1,1,3,5,...,k-2,k+3,...,n,2,4,...,k+1            (k为奇数,n为偶数)
k,k+2,k+4,...,n-2,1,3,5,...,k-2,k+3,...,n-1,2,4,...,k+1,n        (k为奇数,n为奇数)

第二种情况可以认为是，当n为奇数时用最后一个棋子占据最后一行的最后一个位置，然后用n-1个棋子去填充n-1的棋盘，这样就转化为了相同类型且n为偶数的问题。

若k为奇数，则数列的前半部分均为奇数，否则前半部分均为偶数。

4.Code：

http://blog.csdn.net/lyy289065406/article/details/6642789?reload

 1 /*代码一：构造法*/
 2 
 3 //Memory Time 
 4 //188K   16MS 
 5 
 6 #include<iostream>
 7 #include<cmath>
 8 using namespace std;
 9 
10 int main(int i)
11 {
12     int n;  //皇后数
13     while(cin>>n)
14     {
15         if(!n)
16             break;
17 
18         if(n%6!=2 && n%6!=3)
19         {
20             if(n%2==0)  //n为偶数
21             {
22                 for(i=2;i<=n;i+=2)
23                     cout<<i<<' ';
24                 for(i=1;i<=n-1;i+=2)
25                     cout<<i<<' ';
26                 cout<<endl;
27             }
28             else   //n为奇数
29             {
30                 for(i=2;i<=n-1;i+=2)
31                     cout<<i<<' ';
32                 for(i=1;i<=n;i+=2)
33                     cout<<i<<' ';
34                 cout<<endl;
35             }
36         }
37         else if(n%6==2 || n%6==3)
38         {
39             if(n%2==0)  //n为偶数
40             {
41                 int k=n/2;
42                 if(k%2==0)  //k为偶数
43                 {
44                     for(i=k;i<=n;i+=2)
45                         cout<<i<<' ';
46                     for(i=2;i<=k-2;i+=2)
47                         cout<<i<<' ';
48                     for(i=k+3;i<=n-1;i+=2)
49                         cout<<i<<' ';
50                     for(i=1;i<=k+1;i+=2)
51                         cout<<i<<' ';
52                     cout<<endl;
53                 }
54                 else  //k为奇数
55                 {
56                     for(i=k;i<=n-1;i+=2)
57                         cout<<i<<' ';
58                     for(i=1;i<=k-2;i+=2)
59                         cout<<i<<' ';
60                     for(i=k+3;i<=n;i+=2)
61                         cout<<i<<' ';
62                     for(i=2;i<=k+1;i+=2)
63                         cout<<i<<' ';
64                     cout<<endl;
65                 }
66             }
67             else   //n为奇数
68             {
69                 int k=(n-1)/2;
70                 if(k%2==0)  //k为偶数
71                 {
72                     for(i=k;i<=n-1;i+=2)
73                         cout<<i<<' ';
74                     for(i=2;i<=k-2;i+=2)
75                         cout<<i<<' ';
76                     for(i=k+3;i<=n-2;i+=2)
77                         cout<<i<<' ';
78                     for(i=1;i<=k+1;i+=2)
79                         cout<<i<<' ';
80                     cout<<n<<endl;
81                 }
82                 else  //k为奇数
83                 {
84                     for(i=k;i<=n-2;i+=2)
85                         cout<<i<<' ';
86                     for(i=1;i<=k-2;i+=2)
87                         cout<<i<<' ';
88                     for(i=k+3;i<=n-1;i+=2)
89                         cout<<i<<' ';
90                     for(i=2;i<=k+1;i+=2)
91                         cout<<i<<' ';
92                     cout<<n<<endl;
93                 }
94             }
95         }
96     }
97     return 0;
98 }