【分层强化学习】#4 Option-Critic：可学习的选项框架

UVFA通过值函数近似泛化任务目标，并在h-DQN等分层结构中与HRL相结合，实现了不同子目标值函数的高效统一学习，但其根本局限在于子目标本身仍完全依赖于人工设定。作为对UVFA框架的补充与发展，Option-Critic架构在同一时期选择了不同的技术路径。它从策略梯度方法出发，将核心目标设定为让模型自主地发现与学习子目标，从而在选项层面推动更高程度的自动化。

Option-Critic

Option-Critic（选项-评论家，本文简称OC）架构以Actor-Critic架构为基础，采用了选项框架来封装子任务，其设计目的是将选项内化为可学习的部件。回顾一下，在选项框架中，一个选项$\omega \in \Omega$由三元组$({\mathcal{I}}_{\omega },{\pi }_{\omega },{\beta }_{\omega })$描述：

• 初始集${\mathcal{I}}_{\omega }\subseteq \mathcal{S}$：规定了在哪些状态下可以启用这个选项；
• 内部策略${\pi }_{\omega }$：一个底层策略，在执行选项时根据当前状态选择动作$a$；
• 终止函数${\beta }_{\omega }(s)\in [0,1]$：给出选项在状态$s$下终止的概率。

OC假设所有选项$\omega$都能在任意状态下被启用，即初始集${\mathcal{I}}_{\omega }$是整个状态空间$\mathcal{S}$。模型将通过环境奖励学习选项的价值函数，在策略中隐式学习选项的初始集。

选项学习

OC的决策架构由一个上层策略${\pi }_{\Omega }$和所有选项$\omega$的内部策略${\pi }_{\omega }$组成。对于某个状态$s$，智能体首先根据上层策略${\pi }_{\Omega }$选择一个选项$\omega$，并将控制权交由其内部策略${\pi }_{\omega }$。在${\pi }_{\omega }$执行原始动作的每一步，选项的终止函数${\beta }_{\omega }$都会评估当前状态以决定选项是否应该终止。选项终止后，控制权将返回给上层策略${\pi }_{\Omega }$，如此循环往复。

OC选项学习的视角与此前介绍的算法有所不同：

• 选项内部策略的学习不依赖人为设计的内部奖励，而是完全基于环境提供的全局奖励；
• 选项学习的出发点不在于如何将主任务分解为一系列子目标，而是在于评估选项的持续执行价值。

具体而言，OC学习每个选项应该在何时被坚持、何时被终止，即选项的终止函数。其判断依据为继续执行当前选项能否为最终任务带来更高的长期价值。可是内部策略也是我们随机初始化后交给模型同时学习的，这导致我们无从得知内部策略收敛后的具体行动逻辑，但模型确实“学会”了。这种追求自动化的选项学习的代价便是选项可解释性和可重用性的丧失。

在OC中，上层策略${\pi }_{\Omega }$直接根据选项的价值函数做出决策，每个选项的内部策略则由参数为$\theta$的策略网络${\pi }_{\omega ,\theta }$来学习，每个选项的终止函数由参数为$\vartheta$的网络${\beta }_{\omega ,\vartheta }$学习。OC没有限制不同选项的参数是独立还的是共享的，如果参数独立则每个选项都有自己的策略网络和终止函数网络，如果参数共享则策略和终止函数还需接收选项编码作为输入，因此选项的数量和编码方式仍然需要人为设计。

OC最大化的目标函数即为期望累积奖励（即时收益下标为$t+1$而非$t$）

$$\rho (\Omega ,\theta ,\vartheta ,s_0,{\omega }_0)=\mathbb{E}\left[\sum _{t=0}^{\infty }{\gamma }^t{r}_{t+1}|s_0,{\omega }_0\right]$$

梯度定理：准备工作

为了给出选项框架下的策略梯度定理，OC定义了三个相互关联的价值函数，它们共同描述了在选项框架下的决策过程。在状态$s$下，上层策略${\pi }_{\Omega }$选择并开始执行选项$\omega$，随后遵循策略${\pi }_{\omega ,\theta }$直至选项$\omega$终止，并将控制权交还上层策略${\pi }_{\Omega }$以继续进行决策循环，直至整个任务终止。在这个过程中

• 选项价值函数$Q_{\Omega }(s,\omega )$给出${\pi }_{\Omega }$在状态$s$选择选项$\omega$之后的期望累积奖励

$$Q_{\Omega }(s,\omega )={\mathbb{E}}_{a\sim {\pi }_{\omega ,\theta }(\cdot |s)}[Q_U(s,\omega ,a)]$$

• 动作价值函数$Q_U(s,\omega ,a)$给出${\pi }_{\omega ,\theta }$在状态$s$选择动作$a$之后的期望累积奖励

$$Q_U(s,\omega ,a)=r(s,a)+\gamma {\mathbb{E}}_{s^{\prime }\sim P(\cdot |s,a)}[U(\omega ,s^{\prime })]$$

• 抵达时价值函数$U(\omega ,s^{\prime })$给出智能体带着选项$\omega$转移到状态$s^{\prime }$之后的期望累积奖励

$$U(\omega ,s^{\prime })=(1-{\beta }_{\omega ,\vartheta }(s^{\prime }))Q_{\Omega }(s^{\prime },\omega )+{\beta }_{\omega ,\vartheta }(s^{\prime })V_{\Omega }(s^{\prime })$$

该函数即学习终止函数${\beta }_{\omega ,\vartheta }$的关键，它是两种情况的加权平均：

• 选项以$1-{\beta }_{\omega ,\vartheta }(s^{\prime })$的概率不终止，后继回报即在状态$s^{\prime }$下选项$\omega$的价值；
• 选项以${\beta }_{\omega ,\vartheta }(s^{\prime })$的概率终止，后继回报即状态$s^{\prime }$由${\pi }_{\Omega }$重新决策的价值。

最后，由于选项是否终止这一因素的存在，OC定义了MDP在包含选项空间$\Omega$的增强状态空间$\mathcal{S}\times \Omega$下的转移概率，这将用于在梯度定理的推导中得到更简洁的形式

$$P(s_{t+1},{\omega }_{t+1}|s_t,{\omega }_t)={\mathbb{E}}_{a\sim {\pi }_{{\omega }_t,\theta }(\cdot |s_t)}[P(s_{t+1}|s_t,a)\cdot ((1-{\beta }_{{\omega }_t,\vartheta }(s_{t+1}))1_{{\omega }_t={\omega }_{t+1}}+{\beta }_{{\omega }_t,\vartheta }(s_{t+1}){\pi }_{\Omega }({\omega }_{t+1}|s_{t+1}))]$$

其中指示函数$1_{{\omega }_t={\omega }_{t+1}}$在${\omega }_t={\omega }_{t+1}$时为$1$，否则为$0$。该指示函数的意义是，选项不发生变化的概率需要计算“选项不终止”和“选项终止后被上层策略重新选择”两种情况，而选项变化的概率只需要计算“原选项${\omega }_t$终止后上层策略选择指定的新选项${\omega }_{t+1}$”的情况。

内部选项策略梯度定理

现在我们可以推导选项价值函数关于$\theta$的梯度以学习内部策略${\pi }_{\omega ,\theta }$

$$\begin{array}{rl}{\nabla }_{\theta }{Q}_{\Omega }(s,\omega )& ={\nabla }_{\theta }{\mathbb{E}}_{a\sim {\pi }_{\omega ,\theta }(\cdot |s)}[Q_U(s,\omega ,a)]\\ & ={\nabla }_{\theta }\sum _a{\pi }_{\omega ,\theta }(a|s)Q_U(s,\omega ,a)\\ & =\sum _a({\nabla }_{\theta }{\pi }_{\omega ,\theta }(a|s)\cdot Q_U(s,\omega ,a)+{\pi }_{\omega ,\theta }(a|s)\cdot {\nabla }_{\theta }{Q}_U(s,\omega ,a))\\ & =\sum _a({\nabla }_{\theta }{\pi }_{\omega ,\theta }(a|s)\cdot Q_U(s,\omega ,a)+{\pi }_{\omega ,\theta }(a|s)\cdot {\nabla }_{\theta }(r(s,a)+\gamma {\mathbb{E}}_{s^{\prime }\sim P(\cdot |s,a)}[U(\omega ,s^{\prime })]))\\ & =\sum _a({\nabla }_{\theta }{\pi }_{\omega ,\theta }(a|s)\cdot Q_U(s,\omega ,a)+\gamma {\pi }_{\omega ,\theta }(a|s)\sum _{s^{\prime }}P(s^{\prime }|s,a)\cdot {\nabla }_{\theta }U(\omega ,s^{\prime }))\end{array}$$

我们需要进一步推导抵达时价值函数的梯度

$$\begin{array}{rl}{\nabla }_{\theta }U(\omega ,s^{\prime })& ={\nabla }_{\theta }[(1-{\beta }_{\omega ,\vartheta }(s^{\prime }))Q_{\Omega }(s^{\prime },\omega )+{\beta }_{\omega ,\vartheta }(s^{\prime })V_{\Omega }(s^{\prime })]\\ & =(1-{\beta }_{\omega ,\vartheta }(s^{\prime }))\cdot {\nabla }_{\theta }{Q}_{\Omega }(s^{\prime },\omega )+{\beta }_{\omega ,\vartheta }(s^{\prime })\sum _{{\omega }^{\prime }}{\pi }_{\Omega }({\omega }^{\prime }|s^{\prime })\cdot {\nabla }_{\theta }{Q}_{\Omega }(s^{\prime },{\omega }^{\prime })\\ & =\sum _{{\omega }^{\prime }}[(1-{\beta }_{\omega ,\vartheta }(s^{\prime }))1_{\omega ={\omega }^{\prime }}+{\beta }_{\omega ,\vartheta }(s^{\prime }){\pi }_{\Omega }({\omega }^{\prime }|s^{\prime })]\cdot {\nabla }_{\theta }{Q}_{\Omega }(s^{\prime },{\omega }^{\prime })\end{array}$$

现在将其代回选项价值函数的梯度

$$\begin{array}{rl}{\nabla }_{\theta }{Q}_{\Omega }(s,\omega )& =\sum _a({\nabla }_{\theta }{\pi }_{\omega ,\theta }(a|s)\cdot Q_U(s,\omega ,a)+\gamma {\pi }_{\omega ,\theta }(a|s)\sum _{s^{\prime }}P(s^{\prime }|s,a)\cdot \sum _{{\omega }^{\prime }}[(1-{\beta }_{\omega ,\vartheta }(s^{\prime }))1_{\omega ={\omega }^{\prime }}+{\beta }_{\omega ,\vartheta }(s^{\prime }){\pi }_{\Omega }({\omega }^{\prime }|s^{\prime })]\cdot {\nabla }_{\theta }{Q}_{\Omega }(s^{\prime },{\omega }^{\prime }))\\ & =\sum _a{\nabla }_{\theta }{\pi }_{\omega ,\theta }(a|s)\cdot Q_U(s,\omega ,a)+\sum _{s^{\prime },{\omega }^{\prime }}\gamma \sum _a{\pi }_{\omega ,\theta }(a|s)P(s^{\prime }|s,a)[(1-{\beta }_{\omega ,\vartheta }(s^{\prime }))1_{\omega ={\omega }^{\prime }}+{\beta }_{\omega ,\vartheta }(s^{\prime }){\pi }_{\Omega }({\omega }^{\prime }|s^{\prime })]\cdot {\nabla }_{\theta }{Q}_{\Omega }(s^{\prime },{\omega }^{\prime })\end{array}$$

注意到第二项的概率分布包含增强状态空间$\mathcal{S}\times \Omega$下的转移概率，我们记经过$k$次折扣的转移概率为

$$P_{\gamma }^{(k)}(s^{\prime },{\omega }^{\prime }|s,\omega )={\gamma }^{k}P(s^{\prime },{\omega }^{\prime }|s,\omega )$$

则选项价值函数梯度为

$$\begin{array}{rl}{\nabla }_{\theta }{Q}_{\Omega }(s,\omega )& =\sum _a{\nabla }_{\theta }{\pi }_{\omega ,\theta }(a|s)\cdot Q_U(s,\omega ,a)+\sum _{s^{\prime },{\omega }^{\prime }}{P}_{\gamma }^{(1)}(s^{\prime },{\omega }^{\prime }|s,\omega )\cdot {\nabla }_{\theta }{Q}_{\Omega }(s^{\prime },{\omega }^{\prime })\\ \text{（展开递归）}& =\sum _{k=0}^{\infty }\sum _{s^{\prime },{\omega }^{\prime }}{P}_{\gamma }^{(k)}(s^{\prime },{\omega }^{\prime }|s,\omega )\sum _a{\nabla }_{\theta }{\pi }_{\omega ,\theta }(a|s)\cdot Q_U(s,\omega ,a)\end{array}$$

其中折扣转移概率对$k$的求和部分可视为从初始状态选项对$(s_0,{\omega }_0)$开始，智能体访问状态选项对$(s,\omega )$的折扣概率，记为

$${\mu }_{\Omega }(s,\omega |s_0,{\omega }_0)=\sum _{k=0}^{\infty }{P}_{\gamma }^{(k)}(s,\omega |s_0,{\omega }_0)$$

则我们最终得到内部选项策略梯度定理为

$$\begin{array}{rl}{\nabla }_{\theta }{Q}_{\Omega }(s,\omega )& =\sum _{s,\omega }{\mu }_{\Omega }(s,\omega |s_0,{\omega }_0)\sum _a{\nabla }_{\theta }{\pi }_{\omega ,\theta }(a|s)\cdot Q_U(s,\omega ,a)\\ & =\sum _{s,\omega ,a}{\mu }_{\Omega }(s,\omega |s_0,{\omega }_0){\pi }_{\omega ,\theta }(a|s){\nabla }_{\theta }\log {\pi }_{\omega ,\theta }(a|s)\cdot Q_U(s,\omega ,a)\\ & ={\mathbb{E}}_{s,\omega \sim {\mu }_{\Omega },a\sim {\pi }_{\omega ,\theta }(\cdot |s)}[{\nabla }_{\theta }\log {\pi }_{\omega ,\theta }(a|s)\cdot Q_U(s,\omega ,a)]\end{array}$$

该定理优雅地匹配了策略梯度定理的一般形式。

终止梯度定理

（博主实在忍不住拿出原论文的证明过程进行批斗，想挑战自我的可以尝试理解这张图的推导）

现在我们推导目标函数对$\vartheta$的梯度以学习终止函数${\beta }_{\omega ,\vartheta }$。${\beta }_{\omega ,\vartheta }$仅直接参与抵达时价值函数$U(\omega ,s^{\prime })$的计算，我们先初步对抵达时价值函数求梯度

$$\begin{array}{rl}{\nabla }_{\vartheta }U(\omega ,s^{\prime })& ={\nabla }_{\vartheta }((1-{\beta }_{\omega ,\vartheta }(s^{\prime }))Q_{\Omega }(s^{\prime },\omega )+{\beta }_{\omega ,\vartheta }(s^{\prime })V_{\Omega }(s^{\prime }))\\ & ={\nabla }_{\vartheta }{\beta }_{\omega ,\vartheta }(s^{\prime })\cdot (V_{\Omega }(s^{\prime })-Q_{\Omega }(s^{\prime },\omega ))+(1-{\beta }_{\omega ,\vartheta }(s^{\prime }))\cdot {\nabla }_{\vartheta }{Q}_{\Omega }(s^{\prime },\omega )+{\beta }_{\omega ,\vartheta }(s^{\prime })\cdot {\nabla }_{\vartheta }{V}_{\Omega }(s^{\prime })\end{array}$$

将后面两项中的梯度展开

$$\begin{array}{rl}& {\nabla }_{\vartheta }{Q}_{\Omega }(s^{\prime },\omega )=\sum _a{\pi }_{\omega ,\theta }(a|s^{\prime })\sum _{s^{\prime \prime }}\gamma P(s^{\prime \prime }|s^{\prime },a)\cdot {\nabla }_{\vartheta }U(\omega ,s^{\prime \prime })\\ & {\nabla }_{\vartheta }{V}_{\Omega }(s^{\prime })=\sum _{{\omega }^{\prime }}{\pi }_{\Omega }({\omega }^{\prime }|s^{\prime })\sum _a{\pi }_{{\omega }^{\prime },\theta }(a|s^{\prime })\sum _{s^{\prime \prime }}\gamma P(s^{\prime \prime }|s^{\prime },a)\cdot {\nabla }_{\vartheta }U({\omega }^{\prime },s^{\prime \prime })\end{array}$$

由于公式太长，博主不列出将${\nabla }_{\vartheta }{Q}_{\Omega }(s^{\prime },\omega )$和${\nabla }_{\vartheta }{V}_{\Omega }(s^{\prime })$代回${\nabla }_{\vartheta }U(\omega ,s^{\prime })$的完整结果。总之在代回后，如果将选项$\omega$未终止的情况视为${\omega }^{\prime }=\omega$，我们可以得到针对${\nabla }_{\vartheta }U({\omega }^{\prime },s^{\prime \prime })$的概率分布也是增强状态空间$\mathcal{S}\times \Omega$下的转移概率，因此${\nabla }_{\vartheta }U(\omega ,s^{\prime })$可简化为

$$\begin{array}{r}{\nabla }_{\vartheta }U(\omega ,s^{\prime })={\nabla }_{\vartheta }{\beta }_{\omega ,\vartheta }(s^{\prime })\cdot (V_{\Omega }(s^{\prime })-Q_{\Omega }(s^{\prime },\omega ))+\sum _{{\omega }^{\prime },s^{\prime \prime }}{P}_{\gamma }^{(1)}(s^{\prime \prime },{\omega }^{\prime }|s^{\prime },\omega ){\nabla }_{\vartheta }U({\omega }^{\prime },s^{\prime \prime })\end{array}$$

现在记选项的优势函数为

$$A(s,\omega )=Q(s,\omega )-V(s)$$

代入梯度得

$$\begin{array}{rl}{\nabla }_{\vartheta }U(\omega ,s^{\prime })& =-{\nabla }_{\vartheta }{\beta }_{\omega ,\vartheta }(s^{\prime })\cdot A_{\Omega }(s^{\prime },\omega )+\sum _{{\omega }^{\prime },s^{\prime \prime }}{P}_{\gamma }^{(1)}(s^{\prime \prime },{\omega }^{\prime }|s^{\prime },\omega ){\nabla }_{\vartheta }U({\omega }^{\prime },s^{\prime \prime })\\ \text{（展开递归）}& =-\sum _{{\omega }^{\prime },s^{\prime \prime }}\sum _{k=0}^{\infty }{P}_{\gamma }^{(k)}(s^{\prime \prime },{\omega }^{\prime }|s^{\prime },\omega ){\nabla }_{\vartheta }{\beta }_{{\omega }^{\prime },\vartheta }(s^{\prime \prime })\cdot A_{\Omega }(s^{\prime \prime },{\omega }^{\prime })\end{array}$$

与内部选项策略梯度定理类似，将上式的求和转换为从初始选项${\omega }_o$和初始后继状态$s_1$开始，智能体访问后继状态-选项对$(s^{\prime },\omega )$的折扣概率，则最终我们得到终止梯度定理为

$$\begin{array}{rl}{\nabla }_{\vartheta }U({\omega }_0,s_1)& =-\sum _{s^{\prime },\omega }{\mu }_{\Omega }(s^{\prime },\omega |s_1,{\omega }_0){\nabla }_{\vartheta }{\beta }_{\omega ,\vartheta }(s^{\prime })\cdot A_{\Omega }(s^{\prime },\omega )\\ & =-{\mathbb{E}}_{s^{\prime },\omega \sim {\mu }_{\Omega }}[{\nabla }_{\vartheta }{\beta }_{\omega ,\vartheta }(s^{\prime })\cdot A_{\Omega }(s^{\prime },\omega )]\end{array}$$

算法流程

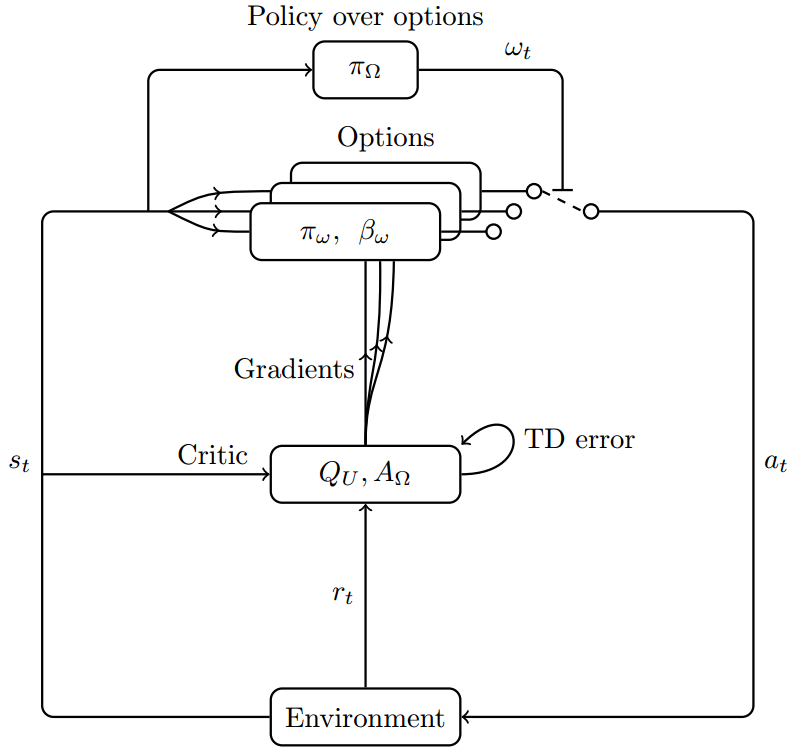
论文中同时提出了表格型Q学习和Q函数逼近两种算法形式，但是只给出了表格型Q学习的伪代码，因此我们也基于表格型Q学习介绍算法流程。$Q_U(s,\omega ,a)$通过TD误差更新，如果后继状态不是终止状态，则估计目标为

$$g_t=r_{t+1}+\gamma \left((1-{\beta }_{{\omega }_t,\vartheta }(s_{t+1}))Q_{\Omega }(s_{t+1},{\omega }_t)+{\beta }_{{\omega }_t,\vartheta }(s_{t+1})\underset{\omega }{\max }{Q}_{\Omega }(s_{t+1},\omega )\right)$$

价值函数$V_{\Omega }(s_{t+1})$基于贪心策略给出，即为$\underset{\omega }{\max }{Q}_{\Omega }(s_{t+1},\omega )$。如果后继状态是终止状态，估计目标$g_t=r_{t+1}$。

$Q_{\Omega }(s,\omega )$则直接由$Q_U(s,\omega ,a)$和${\pi }_{\omega ,\theta }(a|s)$计算，并跟随二者同步更新

$$Q_{\Omega }(s,\omega )=\sum _a{\pi }_{\omega ,\theta }(a|s)Q_U(s,\omega ,a)$$

内部策略${\pi }_{\omega ,\theta }$和终止函数${\beta }_{\omega ,\vartheta }$则分别由内部选项策略梯度和终止梯度更新。终止梯度计算所需的优势函数在梯度更新时计算如下

$$A_{\Omega }(s^{\prime },\omega )=Q_{\Omega }(s^{\prime },\omega )-\underset{{\omega }^{\prime }}{\max }{Q}_{\Omega }(s^{\prime },{\omega }^{\prime })$$

OC算法的伪代码如下：

1. 初始化策略网络参数$\theta ,\vartheta$；
2. 初始化$Q_U(s,\omega ,a)$并计算$Q_{\Omega }(s,\omega )$；
3. 初始化学习率$\alpha ,{\alpha }_{\theta },{\alpha }_{\vartheta }$；
4. 对每一幕循环：
   1. 初始化$s\leftarrow s_0$；
   2. 根据$ϵ$-贪心策略选择选项$\omega$；
   3. 循环直到$s^{\prime }$是终止状态：
      1. 根据内部策略${\pi }_{\omega ,\theta }$选择动作$a$；
      2. 执行动作$a$，观测到后继状态$s^{\prime }$和收益$r$；
      3. 计算TD误差$\delta$；
      4. $Q_U(s,\omega ,a)\leftarrow Q_U(s,\omega ,a)+\alpha \delta$；
      5. $\theta \leftarrow \theta +{\alpha }_{\theta }{\nabla }_{\theta }{Q}_{\Omega }(s,\omega )$；
      6. $\vartheta \leftarrow \vartheta +{\alpha }_{\vartheta }{\nabla }_{\vartheta }U(\omega ,s^{\prime })$；
      7. 更新$Q_{\Omega }(s,\omega )$；
      8. 如果${\beta }_{\omega ,\vartheta }$在$s^{\prime }$终止：
         1. 根据$ϵ$-贪心策略选择新选项$\omega$；
         2. 更新$s\leftarrow s^{\prime }$。