【分层强化学习】#3 UVFA & h-DQN：通用值函数与目标泛化

自MAXQ算法（1999）提出后的十余年间，分层强化学习领域的发展长期受限于两大瓶颈：

• 层次结构严重依赖专家知识进行人工设计；
• 算法以表格型为主，难以处理高维或连续状态空间。

这些局限极大地制约了方法的泛化性与可扩展性，直至深度强化学习的兴起，分层强化学习才迎来了取得实质性突破的转机。

UVFA

UVFA（Universal Value Function Approximators，通用值函数逼近器）引入目标作为值函数的计算模型并交由神经网络学习。其初衷是利用神经网络实现目标的泛化，让单一智能体能完成多种任务，并共享任务间的知识，却间接成为了分层强化学习思想与深度强化学习相结合的奠基性工作。

带目标的值函数

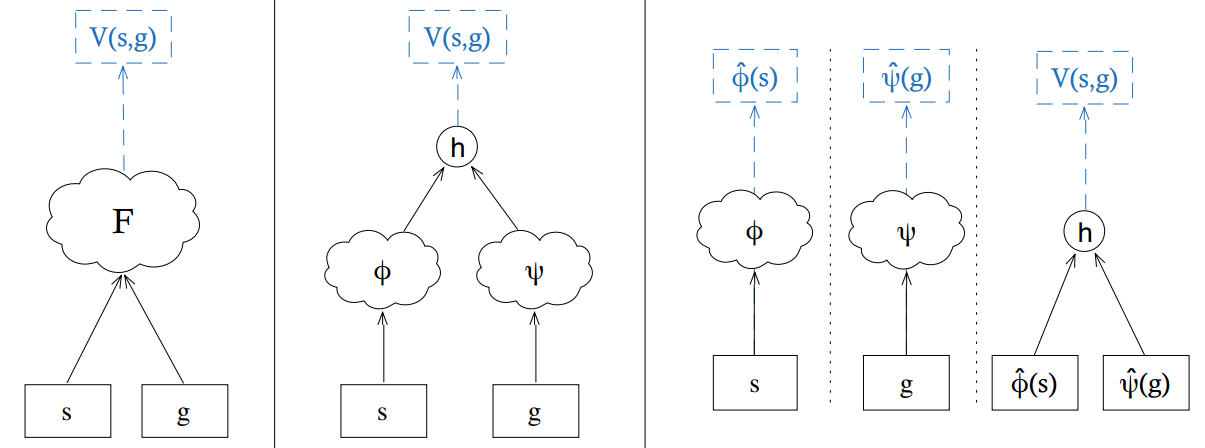
传统的值函数逼近器$V(s|\theta )$主要依赖状态空间$\mathcal{S}$的结构来学习观测状态的值，并将其泛化到未观测状态。而在强化学习中，任务目标$g$通常也体现为期望的状态或状态转移，因此目标空间$\mathcal{G}$往往与状态空间$\mathcal{S}$具有相似的结构特性。基于这一洞察，UVFA将值函数逼近器的输入扩展到为状态$s$和目标$g$两个维度，构建出通用值函数逼近器$V(s,g|\theta )$。一个训练充分的UVFA能够识别并利用状态与目标之间的联合结构，从而学习到任意状态$s$在任意目标$g$下的价值。

UVFA中，伪奖励函数和奖励折扣的实现更加灵活，它提出对于目标$g$和策略$\pi$，含目标的值函数计算定义如下

$$V_{g,\pi }(s)\dot{=}{\mathbb{E}}_{\pi }\left[\sum _{t=0}^{\infty }\left(R_g(s_{t+1},a,s_t)\prod _{k=0}^t{\gamma }_g(s_k)\right)|s_0=s\right]$$

$$Q_{g,\pi }(s,a)\dot{=}{\mathbb{E}}_{\pi }[R_g(s,a,s^{\prime })+{\gamma }_g(s^{\prime })V_{g,\pi }(s^{\prime })]$$

其中

• $R_g(s,a,s^{\prime })$为伪奖励函数，通常设计为参数化函数$R(s,a,s^{\prime }|w_g)$。$w_g$可以是
  • 状态$s$的加权系数，表示对不同状态量的偏好；
  • 目标$g$的某种表示，例如用$g$的坐标根据当前位置到$g$的距离给予奖励；
  • 目标$g$的判断条件，例如为状态$s$设置阈值，根据其是否在阈值范围内给予奖励。
• ${\gamma }_g(s)$为伪折扣系数，其具有两个作用
  • 奖励折扣，能够根据状态$s$和目标$g$灵活调整对未来的规划深度，可以考虑由神经网络学习，但通常我们采取简单的人为设计，并对大部分情况采取统一的外部折扣${\gamma }_{ext}$；
  • 软终止，当状态$s$实现目标$g$时，令${\gamma }_g(s)=0$以截断回报计算。

得益于深度学习强大的表示与学习能力，目标$g$的定义方式也更为灵活多样，具体可包括以下形式：

• 状态子集：指期望达到的某个特定状态，例如目标位置的坐标；
• 状态属性：指状态所需满足的某种属性，例如机器人是否抓持物体；
• 状态映射：指与状态空间相关的另一空间中的表示，例如当状态空间为机器人关节空间时，目标空间可为末端执行器的笛卡尔空间；
• 伪奖励函数：指需要最大化的奖励信号，例如游戏中的金币数量或经验值。

为了将目标$g$作为神经网络的输入，我们还需对其进行合理表示，常用的输入形式包括：

• 原始表示：当目标是状态子集或状态映射时，可直接使用其原始形式作为输入；
• 特征向量：当目标可由一系列属性描述时，用一个$|\mathcal{G}|$维向量表示（$|\mathcal{G}|$为属性总数），每一维对应一个属性的数值或布尔值；
• 独热编码：当目标为离散且数量有限时，用一个$|\mathcal{G}|$维向量表示（$|\mathcal{G}|$为目标总数），目标$g_i$对应的向量在第$i$维为$1$，其余为$0$；
• 函数参数：对于人为设计的参数化的伪奖励函数目标，可以使用伪奖励函数的参数$w_g$作为输入。

总体而言，从原始表示到独热编码，表示方式的复杂性逐渐降低，但其泛化能力也随之减弱，而函数参数的泛化能力由设计方式决定。

因子分解

泛化能力好坏的关键在于相似的目标是否具有相似的表示。在独热编码下，任意目标向量之间均正交，不具有任何相似度信息，模型则无从利用部分已知的目标数据预测未知的目标数据。例如在汉语中，如果我们知道“狗”和“猫”是什么，那我们也能合理推测“狼”大概属于兽类，因为它们具有相同的偏旁，而在英语中知道“dog”和“cat”是不可能猜出“wolf”的任何信息的。但是对于复杂任务中的目标，例如“倒水”和“接水”，人为设计一个能客观反映二者相似信息的数据表示是不可能的。

向值函数引入额外输入$g$也为其学习带来了新的挑战，因为与单一的状态空间相比，状态-目标组合的数量呈指数级增长，而我们却难以进一步获取更多的数据，导致数据稀疏性问题显著加剧。一方面相应的算力、时间成本也会增加，另一方面许多状态-目标组合是无意义或不可行的。例如机器人以“在厨房”为初始状态实现“冲马桶”的目标，显然设置一个“在卫生间”的中间目标会合理得多。或者让只能水平移动的平台立起一个已经倒下的倒立摆，这违背了物理定律。

这是一个广泛存在于大规模机器学习的问题，即稀疏矩阵问题。如果以状态$s$为行，目标$g$为列，值函数$V(s,g)$为元素，则该数据矩阵的绝大多数都为零。尽管其具有良好的可解释性，但是却给模型泛化训练带来困难，尤其是当我们的状态和目标表示本身的泛化能力就不足时。

我们无法改变数据稀疏这一客观约束（至少是从机器学习算法层面），只能从表示上的泛化入手。一个普遍方法是嵌入向量，其核心思想是利用神经网络改进人为设计的表示方法，即让神经网络将高维稀疏空间中的对象映射到一个低维稠密空间，学会从非结构化的、缺乏语义的数据表示中捕捉到隐含的语义信息和内在联系，最终输出的表示即为嵌入向量。由嵌入向量给出的数据点具有更高的信息密度，通过泛化可以弥补更多的数据空白。例如我们对世界上所有的城市进行独热编码作为模型输入来估计任意两个城市之间的距离，直接训练需要海量的测量数据，因为一对城市的距离对模型推断其他城市对的距离的帮助是极低的。但是通过引入嵌入层，模型很可能会利用嵌入层学习到每个城市的经纬度作为嵌入向量，由此算出任意城市对的距离便水到渠成了。不过实际上出于嵌入向量可解释性不足的缺点，我们完全无法知道嵌入层会学习到何种表示。

嵌入向量在UVFA中的应用被称为因子分解。原始的UVFA合并状态$s$和目标$g$输入到网络$F$计算$V(s,g)$，而因子分解先用两个独立子网络$\varphi$和$\psi$的双流架构学习状态$s$到状态嵌入$\varphi (s)$和目标$g$到目标嵌入$\psi (g)$的映射，再将二者合并输入到网络$h$计算$V(s,g)$。嵌入网络跟随整个价值估计任务一同进行端到端的训练。论文中采用了数据矩阵的低秩分解得到嵌入向量的标签值，但这涉及矩阵分解理论，且与端到端训练效果等价，故本文不作探讨。

h-DQN

h-DQN（Hierarchical Deep Q-Network，分层深度Q网络）将UVFA的核心思想与分层强化学习相结合，设计出了元控制器-控制器双层架构。

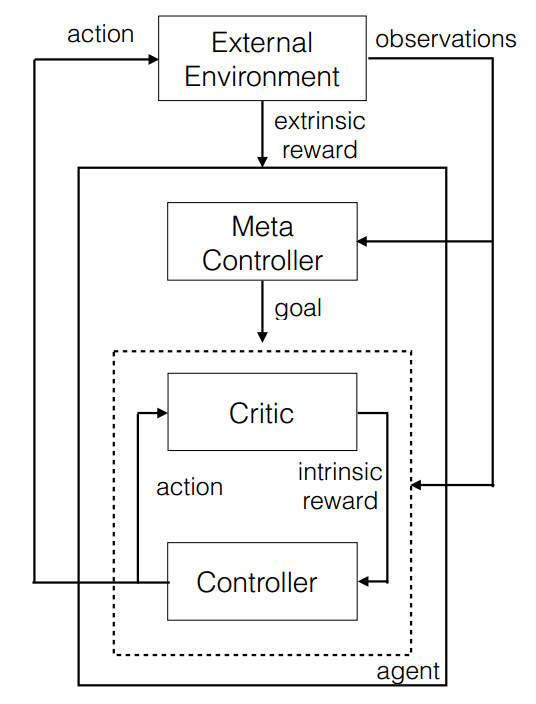
元控制器-控制器

（论文中控制器下标为$1$，元控制器下标为$2$，但博主认为按照与下标相反的顺序介绍二者更合逻辑）

元控制器负责接收状态$s_t$并为控制器由策略${\pi }_g$选择子目标$g_t\in \mathcal{G}$，其目标函数是最大化累积环境奖励

$$F_t=\sum _{t^{\prime }=t}^{\infty }{\gamma }^{t^{\prime }-t}{f}_{t^{\prime }}$$

总目标即由元控制器从环境奖励中学习，由此元控制器的估计目标形式即为一般的动作价值函数，只是子目标$g$替换了动作$a$

$$Q_2^{\ast }(s,g)=\underset{{\pi }_g}{\max }\mathbb{E}\left[\sum _{t^{\prime }=t}^{t+N}{f}_{t^{\prime }}+\gamma \underset{g^{\prime }}{\max }{Q}_2^{\ast }(s_{t+N},g^{\prime })|s_t=s,g_t=g,{\pi }_g\right]$$

（该式与最大化累积环境奖励的目标不一致。累积环境奖励$F_t$的计算似乎是从单个时间步的尺度对$f_{t^{\prime }}$进行折扣的，但是$Q_2^{\ast }(s,g)$的计算却对每个子目标执行过程中的$f_{t^{\prime }}$简单累加，仅在子目标决策的宏观时间步进行折扣。这是h-DQN论文中一个令人费解的矛盾，文中没有任何解释，博主暂时推测其目的是为了让元控制器进一步从宏观层面学习长期的战略价值）

控制器则接收状态$s_t$，并根据元控制器下达的子目标$g_t$由子策略${\pi }_{ag}$选择动作$a_t$，其目标函数是最大化累积内部奖励

$$R_t(g)=\sum _{t^{\prime }=t}^{\infty }{\gamma }^{t^{\prime }-t}{r}_{t^{\prime }}(g)$$

控制器的估计目标也相应地采用了带目标的价值函数

$$Q_1^{\ast }(s,a;g)=\underset{{\pi }_{ag}}{\max }\mathbb{E}\left[r_t+\gamma \underset{a^{\prime }}{\max }{Q}_1^{\ast }(s^{\prime },a^{\prime };g)|s_t=s,a_t=a,g_t=g,{\pi }_{ag}\right]$$

由于DQN采取最大化操作得到最优动作价值函数，因此对于元控制器，目标空间$\mathcal{G}$实际上被限制为离散的，而控制器则利用来自元控制器离散的$g$点对连续的目标空间进行拟合。

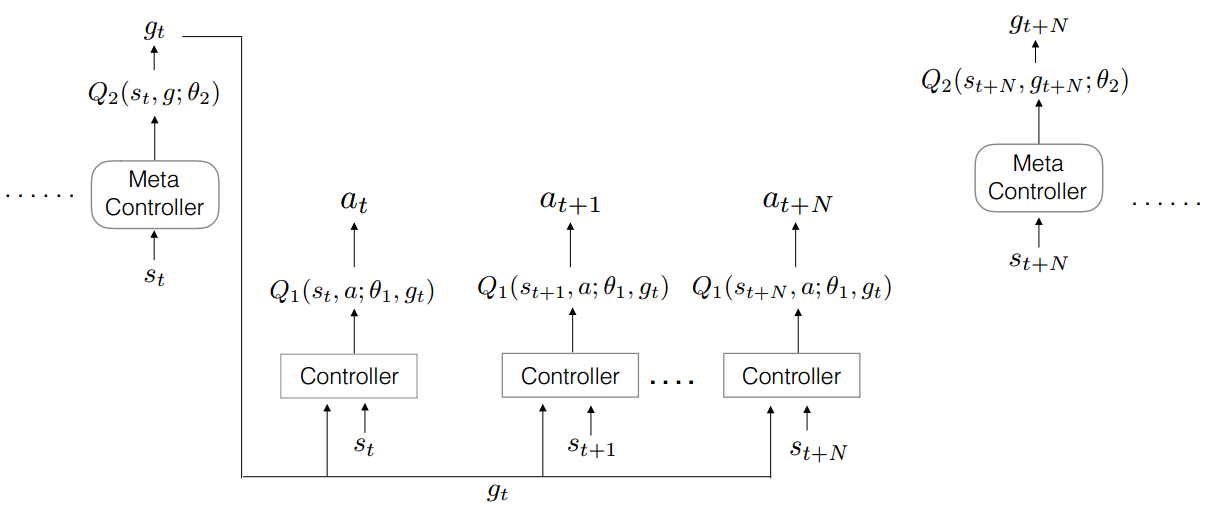
学习算法

现在，我们可以用两个Q网络$Q_2(s,g;{\theta }_2)$和$Q_1(s,a;{\theta }_1,g)$来拟合最优价值函数$Q_2^{\ast }(s,g)$和$Q_1^{\ast }(s,a;g)$。我们采用经验回放，将两个网络的经验$(s_t,g_t,f_t,s_{t+N})$和$(s_t,a_t,g_t,r_t,s_{t+1})$分别存入${\mathcal{D}}_2$和${\mathcal{D}}_1$，则$Q_1$的损失函数为

$$L_1({\theta }_1)={\mathbb{E}}_{(s,a,g,r,s^{\prime })\sim {\mathcal{D}}_1}[(r_t+\gamma \underset{a^{\prime }}{\max }{Q}_1^{\ast }(s^{\prime },a^{\prime };g)-Q_1(s,a,;{\theta }_1,g){)}^2]$$

其梯度为

$${\nabla }_{{\theta }_1}{L}_1({\theta }_1)={\mathbb{E}}_{(s,a,g,r,s^{\prime })\sim {\mathcal{D}}_1}[(r_t+\gamma \underset{a^{\prime }}{\max }{Q}_1^{\ast }(s^{\prime },a^{\prime };g)-Q_1(s,a,;{\theta }_1,g)){\nabla }_{{\theta }_1}{Q}_1(s,a;{\theta }_1,g)]$$

（论文在后续伪代码中又将${\mathcal{D}}_1$中的样本不严谨地记为({s,g},a,r,{s′,g})(\{s,g\},a,r,\{s',g\})({s,g},a,r,{s′,g})，博主只能理解为后继状态中的$g$实际上为后继目标$g^{\prime }$）

$Q_2$的损失函数及其梯度的形式与$Q_1$相似。

h-DQN采取$ϵ$-贪心策略进行探索，其中$ϵ$相当于探索率。控制器和元控制器采用不同的探索率${ϵ}_{1,g}$和${ϵ}_2$，并且初始值均设为$1$。元控制器的探索率${ϵ}_2$随时间推移减小（退火），而控制器的探索率${ϵ}_{1,g}$的退火则依赖于达到特定子目标$g$的平均成功率，平均成功率越高，则可以降低探索率以稳定现有策略，反之则继续维持高探索率。

h-DQN算法的伪代码如下：

1. 初始化经验回放缓存区{D1,D2}\{\mathcal D_1,\mathcal D_2\}{D1​,D2​}和网络参数{θ1,θ2}\{\theta_1,\theta_2\}{θ1​,θ2​}；
2. 初始化控制器对所有目标的探索率和元控制器的探索率${ϵ}_{1,g}={ϵ}_2=1$；
3. 对每一幕循环：
   1. 初始化当前状态$s$；
   2. 根据${ϵ}_2$-贪心选择子目标$g$；
   3. 循环直到$s$为终止状态：
      1. 初始化累积环境奖励$F=0$；
      2. 初始化初始状态$s_0=s$；
      3. 循环直到$s$为终止状态或实现目标$g$：
         1. 根据${ϵ}_{1,g}$-贪心选择动作$a$；
         2. 执行$a$，获得后继状态$s^{\prime }$和环境奖励$f$；
         3. 从内部评估器获得内部奖励$r(s,a,s^{\prime })$；
         4. 存储经验({s,g},a,r,{s′,g′})(\{s,g\},a,r,\{s',g'\})({s,g},a,r,{s′,g′})到${\mathcal{D}}_1$；
         5. 从${\mathcal{D}}_1$中随机抽取小批量对${\theta }_1$进行梯度下降；
         6. 从${\mathcal{D}}_2$中随机抽取小批量对${\theta }_2$进行梯度下降；
         7. 更新累积环境奖励$F\leftarrow f$；
         8. 更新当前状态$s\leftarrow s^{\prime }$。
      4. 存储经验$(s_0,g,F,s^{\prime })$到${\mathcal{D}}_2$；
      5. 如果$s$不是终止状态：
         1. 根据${ϵ}_2$-贪心选择子目标$g$。
   4. 对${ϵ}_2$进行退火，并根据达到目标$g$的平均成功率对${ϵ}_{1,g}$进行自适应退火。