在深度分层强化学习的早期发展过程中,大多数算法均停留在双层架构的设计,而未能向真正的多层取得突破。其核心原因在于,当层次超过两层时,会引发一系列连锁反应,放大分层强化学习的诸多缺陷,使得简单地扩展双层架构变得极其困难:
- 非平稳性:低层策略的同时更新会带来高层策略的动作变得非平稳,这一问题在HIRO开篇介绍过,HIRO也提供了一个重要的解决思路;
- 信用分配级联:最高层的决策需要经过很多步才能最终影响到环境,如果任务失败,将很难判断是哪一个中间层的子目标有误;
- 高层训练信号稀疏:高层策略极低的行动频率意味着其获得反馈的间隔极其漫长,学习速度缓慢。
HAC
HAC(Hierarchical Actor-Critic,分层演员-评论家)的提出正是为了系统性解决深度分层强化学习从双层到多层面临的难题。它在HIRO的基础上,进一步优化了经验复用的方法,并引入子目标测试机制,使得高层策略的训练更加稳定而高效,通过一整套工程解决方案,最终实现了真正有效的多层策略学习架构。
分层架构与嵌套策略
HAC使用UMDP(Universal MDP,通用马尔可夫决策过程)来定义分层强化学习任务。一个UMDP由一个六元组U=(S,G,A,T,R,γ)\mathcal U=(\mathcal S,\mathcal G,\mathcal A,T,R,\gamma)U=(S,G,A,T,R,γ)描述,元组内元素依次为状态空间S\mathcal SS、目标空间G\mathcal GG、动作空间A\mathcal AA、状态转移函数TTT、奖励函数RRR和折扣率γ\gammaγ。
HAC分层架构包含kkk个层级,每个层级有:
- 各自的UMDPU0,⋯ ,Uk−1\mathcal U_0,\cdots,\mathcal U_{k-1}U0,⋯,Uk−1;
- 独立的策略π0,⋯ ,πk−1∈Πk−1\pi_0,\cdots,\pi_{k-1}\in\Pi_{k-1}π0,⋯,πk−1∈Πk−1,πi:Si,Gi→Ai,0≤i≤k−1\pi_i:\mathcal S_i,\mathcal G_i\rightarrow\mathcal A_i,0\leq i\leq k-1πi:Si,Gi→Ai,0≤i≤k−1,其中:
- 状态空间与原始问题的状态空间一致:Si=S\mathcal S_i=\mathcal SSi=S;
- 目标空间与状态空间一致:Gi=S\mathcal G_i=\mathcal SGi=S;
- 高层策略πi(1≤i≤k−1)\pi_i(1\leq i\leq k-1)πi(1≤i≤k−1)输出的动作为目标,即动作空间与状态空间也一致:Ai=S\mathcal A_i=\mathcal SAi=S;
- 底层策略π0\pi_0π0输出原始动作,其动作空间与原始动作空间一致:A0=A\mathcal A_0=\mathcal AA0=A。
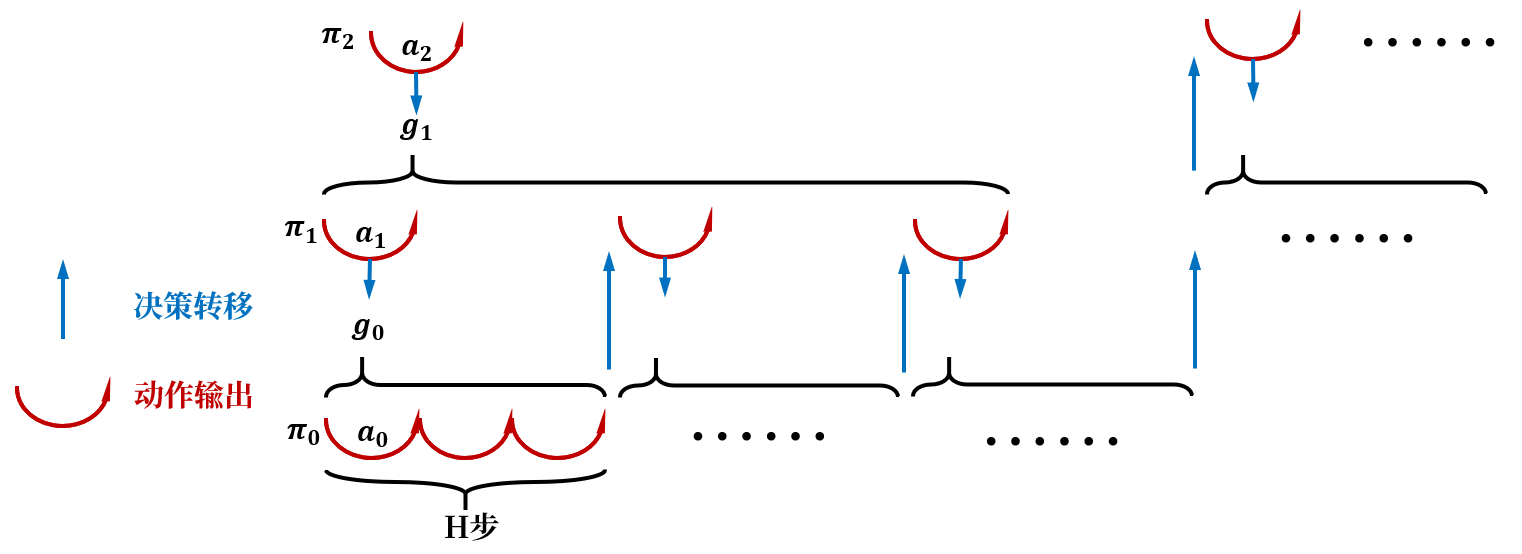
HAC通过嵌套策略实现问题分解,一个自上而下的决策流程为:
- 高层策略πi\pi_iπi根据当前目标gig_igi和状态sis_isi,输出动作aia_iai;
- 第i−1i-1i−1层接收来自第iii层的动作aia_iai作为其目标gi−1g_{i-1}gi−1;
- 低层策略πi−1\pi_{i-1}πi−1根据目标gi−1g_{i-1}gi−1和状态si−1s_{i-1}si−1,输出动作ai−1a_{i-1}ai−1;
- ⋯\cdots⋯
- 第000层接收来自第111层的动作a1a_1a1作为其目标g0g_0g0;
- 底层策略π0\pi_0π0根据目标g0g_0g0和状态s0s_0s0,输出动作a0a_0a0由智能体执行。
- ⋯\cdots⋯
决策自下而上的返回则依赖于高层iii状态转移TiT_iTi的结束条件,会在以下两种情况被低层i−1i-1i−1触发:
- 低层策略πi−1\pi_{i-1}πi−1执行了HHH步仍未达成来自高层的目标gi−1g_{i-1}gi−1;
- 低层策略πi−1\pi_{i-1}πi−1在HHH步内达成了来自高层的目标gi−1g_{i-1}gi−1,或者意外达成了更高层的目标gk(k>i−1)g_k(k>i-1)gk(k>i−1)。
HHH是每一层进行决策的固定时间跨度。
事后动作转移
HAC的多层嵌套策略将在训练中导致更严重的非平稳性。一方面低层策略的更新会带来高层策略所处环境的变化;另一方面HAC的每一层采用确定性策略,低层策略在训练时为了探索会使用带高斯噪声的行为策略πib=πi+N(0,σ2)\pi_{ib}=\pi_i+\mathcal N(0,\sigma^2)πib=πi+N(0,σ2),即使参数固定,高层策略也会观察到随机且不一致的结果。
HAC通过一个巧妙的假设为高层策略人为创造了一个稳定的理想化的学习环境。对于每个高层策略πi\pi_iπi,HAC假设其下属的所有低层策略Πi−1\Pi_{i-1}Πi−1都是最优策略Πi−1∗\Pi_{i-1}^*Πi−1∗来屏蔽非平稳性。这一假设由事后动作转移(Hindsight Action Transition)来实现,其思想与HIRO的离策略校正一脉相承。我们考虑一个简单的双层HAC架构,它的任务是指导智能体到达黄旗的位置。
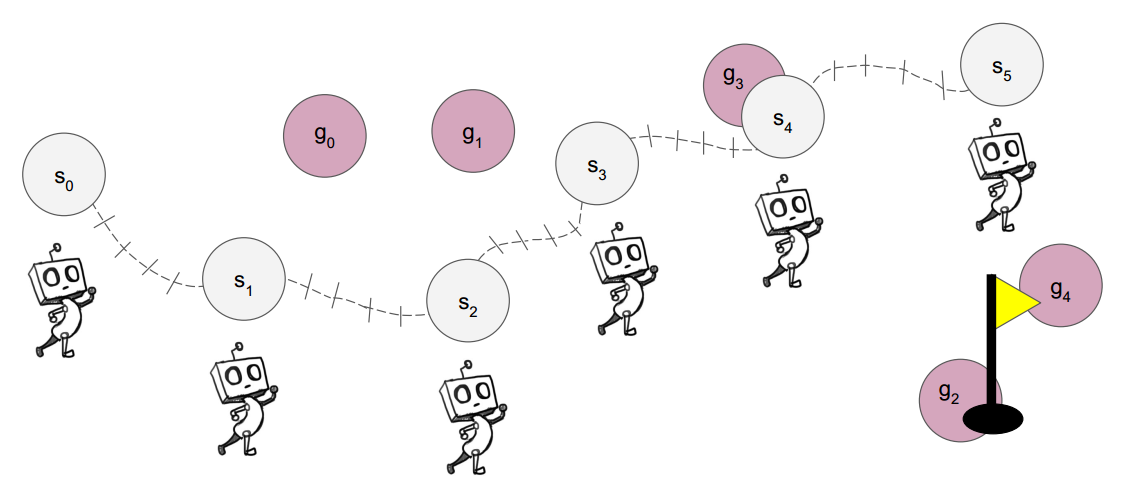
在状态s0s_0s0,高层策略π1\pi_1π1给出目标g0g_0g0,低层策略π0\pi_0π0执行H=5H=5H=5步后到达s1s_1s1,再由高层策略π1\pi_1π1给出目标g1g_1g1,以此类推。一次状态转移TTT产生的经验是由转移前状态sss、输出动作aaa、转移结束时状态s′s's′、来自高层的目标ggg和未来价值折扣率γ\gammaγ组成的五元组(s,a,s′,g,γ)(s,a,s',g,\gamma)(s,a,s′,g,γ)。。以g0g_0g0产生的状态转移为例,高层策略π1\pi_1π1收集的经验为(s0,a=g0,r,s′=s1,gtotal=黄旗,γ)(s_0,a=g_0,r,s'=s_1,g_{total}=黄旗,\gamma)(s0,a=g0,r,s′=s1,gtotal=黄旗,γ)。
事后动作转移的关键是动作重构,其核心思想是“做了什么”比“想做什么”更重要。我们可以认为,对于高层策略π1\pi_1π1给出的任何理论可行的目标,一个最优低层策略π0∗\pi_0^*π0∗应当都能够在HHH步内抵达。如果π0\pi_0π0在实际执行过程中实现了这一点,那么我们自然可以视这条经验来自于最优低层策略π0∗\pi_0^*π0∗。如果π0\pi_0π0实际执行失败了,如图中智能体从s0s_0s0开始按目标g0g_0g0执行却到达了较远的s1s_1s1,HAC将进行事后处理,修正经验中的动作g0g_0g0为s1s_1s1。如此一来,原先在目标g0g_0g0下由π0\pi_0π0产生的失败经验,被转化为了在目标s1s_1s1下可以被视为由π0∗\pi_0^*π0∗产生的成功经验,高层策略π1\pi_1π1也将学习在s0s_0s0选择去s1s_1s1而非g0g_0g0对于达成黄旗目标的价值。
经验中奖励函数rrr的设计遵循两条原则。一是我们只能保证最优低层策略π0∗\pi_0^*π0∗可以达成的结果,而无法预知其具体会走哪条路径,因此奖励函数应与低层策略执行路径无关;二是奖励函数应激励高层策略找到最短路径。为此,HAC采用了一个极其简单的稀疏奖励,即如果达到的状态等于本层的目标(或足够接近),则奖励r=0r=0r=0,否则r=−1r=-1r=−1。
最终,π1\pi_1π1在s0s_0s0输出动作g0g_0g0后到达s1s_1s1产生的经验为(s0,a=s1,r=−1,s′=s1,gtotal=黄旗,γ)(s_0,a=s_1,r=-1,s'=s_1,g_{total}=黄旗,\gamma)(s0,a=s1,r=−1,s′=s1,gtotal=黄旗,γ)。
事后目标转移
事后动作转移通过修正高层策略输出给低层策略的动作aaa,保证了高层策略的训练稳定性。而事后目标转移(Hindsight Goal Transition)则通过修正当前层的目标ggg,通过缓解稀疏奖励问题以保证每一层策略的训练效率。
仍以黄旗任务为例,图中高层策略π1\pi_1π1在一轮决策完毕时,共收集了从s0s_0s0到s5s_5s5的555条原始经验,但是如果我们直接使用原始经验中的gtotal=黄旗g_{total}=黄旗gtotal=黄旗来训练策略π1\pi_1π1,那么它们都会因为没有达到gtotalg_{total}gtotal而产生负奖励r=−1r=-1r=−1,这样的稀疏奖励将导致π1\pi_1π1无法学到成功的经验。为了让π1\pi_1π1能学到至少一条成功的经验,HAC将当前层目标修正为s5s_5s5,由此从s4s_4s4到达s5s_5s5产生的经验会变为r=0r=0r=0的成功经验,在gtotal=黄旗g_{total}=黄旗gtotal=黄旗下的555条失败经验被重标定为了在g~total=s5\tilde g_{total}=s_5g~total=s5下的444条失败经验和111条成功经验。这样一来,即使低层策略永远无法在HHH步内达到高层设定的目标,它也能通过事后目标转移不断获得关于达成可实现目标的成功经验,为网络提供了稳定的学习梯度。
在具体算法实现中,当发生一次状态转移时,HAC会同时创建两条经验,一条为基于原始目标的标准经验,另一条为奖励和目标被擦除(用TBD表示),等待事后处理填充的待定经验。当收集完HHH步产生的所有经验后,HAC将随机从这HHH步的每一步到达的状态中随机选nnn个状态作为当前层的nnn个目标,再将每个新目标分别填充到所有经验的目标中并计算奖励,生成H×nH\times nH×n条事后经验,其中将至少包含nnn条成功经验。原始的标准经验也会用于训练策略,以防其偏离真实的任务目标。
诸如HIRO的离策略校正、HAC的事后动作转移和事后目标转移这类利用“重新解释失败经历”机制对经验进行修正的方法,被称为事后经验回放(Hindsight Experience Replay,HER),有效地解决了深度分层强化学习中的稀疏奖励问题。
子目标测试
仅凭事后动作转移和事后目标转移将带来两个缺陷,它们均源于高层策略对低层策略的认知与实际情况出现了偏差:
- 高层策略πi\pi_iπi将只能学习到当前低层策略πi−1\pi_{i-1}πi−1在HHH步内能实现的子目标(动作)的Q值,而忽略更遥远的子目标的Q值学习。并且随着训练推移,即便πi−1\pi_{i-1}πi−1可达范围扩大,πi\pi_iπi也无法及时认识到这种能力增长。一旦网络初始化对初期πi−1\pi_{i-1}πi−1可达范围外的子目标产生了高估或低估,πi\pi_iπi将难以纠正其偏差,从而导致智能体行为不稳定;
- 高层策略πi\pi_iπi可能会执着于在之前的尝试中发现的最短路径,然而低层策略的能力是动态变化的,可能因探索和泛化而遗忘某些特定技能,导致这条最短路径在当前时刻无法实现,这对高层策略而言也不能被有效地觉察。
尽管Critic网络对Q值的学习具有一定的泛化能力,即可以通过学习当前低层策略可达范围边界的Q值间接地、模糊地学习到稍远的Q值,这对高层策略与低层策略之间信息对齐的帮助也较为有限。为了缓解这一偏差,HAC提出了子目标测试(Subgoal Testing Transitions)来帮助高层策略跟进对低层策略可达范围的学习。当高层策略πi\pi_iπi选择了子目标aaa后,会有λ\lambdaλ的概率进入测试模式。在测试模式下,下属低层策略Πi−1\Pi_{i-1}Πi−1将关闭探索噪声,严格遵循当前的学习策略执行。测试模式将根据不同的执行结果产生经验:
- 如果低层策略πi−1\pi_{i-1}πi−1在HHH步内成功达成子目标,则一切照常,不产生特殊经验;
- 如果低层策略πi−1\pi_{i-1}πi−1在HHH步内失败了,则为高层策略πi\pi_iπi创建一条子目标测试经验(s,a,r=−H,s′,g,γ=0)(s,a,r=-H,s',g,\gamma=0)(s,a,r=−H,s′,g,γ=0),其关键在于:
- 奖励r=−Hr=-Hr=−H给出严重惩罚,相当于浪费了整个时间跨度;
- 折扣率γ=0\gamma=0γ=0不考虑未来状态价值,即这是一个固定的即时收益,不会因为未来状态价值随着低层策略学习改变而改变。
下面我们分三种情况来理解子目标测试如何塑造Q值:
- 绝对不可达的子目标,即最优低层策略也无法在HHH步内达成的子目标。此时子目标测试会稳定地提供−H-H−H的惩罚,使Q值收敛到−H-H−H,让高层策略避开;
- 当前即可达的子目标。此时子目标测试通常会成功,Q值主要由事后经验决定,不受子目标测试干扰;
- 理论可达但当前无法实现的子目标,即最优低层策略可达,但当前低层策略做不到。此时Q值是大量事后经验泛化学习和少量子目标测试经验惩罚的加权平均(测试经验权重收敛于测试概率λ\lambdaλ),并随着低层策略逐渐扩大可达范围,最终能熟练达成该子目标时,Q值将上升到其理论值。
总而言之,HAC以嵌套策略为框架,通过事后动作转移解决层级间的非平稳性问题,通过事后目标转移解决层级内的稀疏奖励问题,再利用子目标测试解决前两者导致的高层策略对低层策略的认知偏差,实现了稳定、高效且安全的多层并行学习。
算法流程
对于每一层策略Actor网络和价值函数Critic网络的训练,HAC采用了DDPG算法。HAC算法的伪代码如下:
- 初始化:
- 超参数:层级数量kkk,最大时间跨度HHH,子目标测试概率λ\lambdaλ,折扣因子γ\gammaγ;
- 每一层的Actor网络和Critic网络。
- 对每一幕循环:
- 初始化状态s←Sinits\leftarrow S_{init}s←Sinit和总目标g←Gk−1g\leftarrow G_{k-1}g←Gk−1;
- 运行训练函数train_level(k−1,s,g)train\_level(k-1,s,g)train_level(k−1,s,g);
- 根据DDPG算法并行更新所有Actor网络和Critic网络。
其中训练函数trainlevel(i,s,g)train_level(i,s,g)trainlevel(i,s,g)是一个递归函数,其伪代码如下:
- 输入层级iii,状态sss,目标ggg;
- 初始化状态si←ss_i\leftarrow ssi←s和目标gi←gg_i\leftarrow ggi←g;
- 循环HHH步或直到实现高层目标gn,i≤n<kg_n,i\leq n<kgn,i≤n<k:
- 输出动作ai←πi(si,gi)+noise(非子目标测试)a_i\leftarrow\pi_i(s_i,g_i)+noise(非子目标测试)ai←πi(si,gi)+noise(非子目标测试);
- 如果i>0i>0i>0:
- 决定是否测试子目标aia_iai;
- 获取后继状态si′←train_level(i−1,si,ai)s_i{'}\leftarrow train\_level(i-1,s_i,a_i)si′←train_level(i−1,si,ai)。
- 否则:
- 执行原始动作a0a_0a0并观测后继状态s0′s_0{'}s0′。
- 如果i>0i>0i>0并且未实现aia_iai:
- 如果aia_iai被测试:
- 将测试经验(s=si,a=ai,r=−H,s′=si′,g=gi,γ=0)(s=s_i,a=a_i,r=-H,s'=s_i{'},g=g_i,\gamma=0)(s=si,a=ai,r=−H,s′=si′,g=gi,γ=0)存入经验缓存区。
- 事后动作转移ai←si′a_i\leftarrow s_i{'}ai←si′。
- 如果aia_iai被测试:
- 将标准经验(s=si,a=ai,r∈{−1,0},s′=si′,g=gi,γ=γ)(s=s_i,a=a_i,r\in\{-1,0\},s'=s_i{'},g=g_i,\gamma=\gamma)(s=si,a=ai,r∈{−1,0},s′=si′,g=gi,γ=γ)存入经验缓存区;
- 将待定经验(s=si,a=ai,r=TBD,s′=si′,g=TBD,γ=γ)(s=s_i,a=a_i,r=TBD,s'=s_i{'},g=TBD,\gamma=\gamma)(s=si,a=ai,r=TBD,s′=si′,g=TBD,γ=γ)存入待定经验缓存区;
- 更新状态s←si′s\leftarrow s_i{'}s←si′。
- 事后目标转移:将待定经验缓存区中的待定经验填充为事后经验存入经验缓存区。
- 返回si′s_i{'}si′。





















 1623
1623

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








