【中国剩余定理】互素与不互素的情况详解

侵权则删（这个现在更多是作为笔记存在，因为写的时间有点久了，不知道参考了多少篇资料汇总的，发现的话会补上的，也非常感谢在网上分享知识的人）

这篇文章很少涉及特别基础的数学公式，但是相信能够帮助你理解，因为笔者的数学水平目前也就学了一点高数。

一个整数除以3余2、除以5余3、除以7余2，求这个整数。
答案：23

模数互素指的是3，5，7的最大公约数为1.。

lcm(a, b)指的是a和b的最小公倍数

gcd(a, b) 指的是a和b的最大公约数

情况一：模数互素

以上面的情况为例，

X = 2(mod 3)

X = 3(mod 5)

X = 2(mod 7)

找到三个数：

X1除以3余2、除以5余0、除以7余0；

X2除以3余0、除以5余3、除以7余0；

X3除以3余0、除以5余0、除以7余2；

X = X1+ X2+X3

设三个数a, b, c  (N 从0 到求余的数，直至找到适宜的为止)

(5 * 7 * N) %3 = 2    X1 =5 * 7 * N = 35

(3 * 7 * N) % 5 = 3    X2 = 3 * 7 * N = 63

(3 * 5 * N) % 7 =2    X3 = 3 * 5 * N = 30

X = X1+ X2+X3 = 128，但此时X不一定为最小解，X % lcm(3, 5, 7) 才为最小解，即23.

情况2：模数不互素

x≡c1 (mod m1)

x≡c2(mod m2)

↓↓

x=m1x1+c1

x=m2x2+c2

↓↓

m1x1+c1=m2x2+c2

↓↓

m1x1=(c2−c1)+m2x2

↓↓

m1x1≡ (c2−c1) (mod m2)

根据数学同余定理（如果一个除法式子的余数为C，则若被除数乘k倍，余数也变为k倍）

要上述式子要有解，gcd(m1,m2)|(c2−c1) ，解释为(c2−c1) 是gcd(m1,m2)的倍数，

 (c2-c1)%gcd(m1,m2)==0时候有解

注意这里每次求得的解都要保证是最小的解的形式，可以通过用(x%mod+mod)%mod 的形式来控制

设d = gcd(m1, m2)

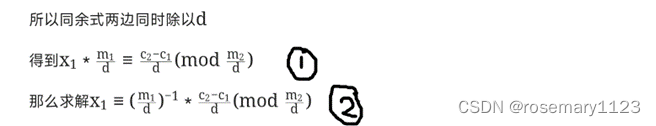
由式1得到式2需要

 3式与4式基本相同，则式2求毕。

 解释前一句：

   两个数的乘积等于它们的最大公约数和最小公倍数的乘积，即

m1 *m2 = lcm(m1, m2) * gcd(m1, m2)

以下是C语言的代码：里面一些gcd函数等等在下面还有介绍

"""c
#include <stdio.h>
#include <math.h>
#include <malloc.h>
#define ll long long
//int lcm(int x,int y,int gcd)
//{return (x * y) / gcd;	}

int exgcd(int a,int b,int *x,int *y)
{
    if(b==0)
    {
        *x=1,*y=0;
        return a;
    }
    int d=exgcd(b,a%b,x,y);
    int k= *x;
    *x= *y;
    *y=k-a/b*(*y);
    return d;
}

int main(){
	int n;
	scanf("%d", &n);
	int nums[n][2];
	int a[n][2];
	int ai = 0; // 数组a的下标 
	int i;
	int j;
	for(i = 0;i < n;i++)
	   for(j = 0;j < 2;j++)
	      scanf("%d", &nums[i][j]);
	int gcd;
	int lcm; 
	int flag = 0;     
	int k1;
	int k2;
	//数组中是否有互质，若有，则将两个互质的数组合并为一组，把合并后的数值填入后一组 
	for(i = 0;i < n;i++){
		for(j = i + 1;j < n;j++){
			int gcd = exgcd(nums[i][0], nums[j][0], &k1, &k2);
			if(gcd != 1){
				flag = 1;
				if((nums[i][1] - nums[j][1])%gcd != 0){
					printf("无解");
					return 0; 
				}
				// 若 C1 减 C2 == 0，则组合后的除数是原先数组的最小公倍数，余数不变 
				if(nums[i][1] - nums[j][1] == 0){
					lcm = (nums[i][0] * nums[j][0]) / gcd;
					nums[j][0] = lcm;
				}
				else{
					int mod = nums[j][0] / gcd;
					int X = k1*(nums[j][1] - nums[i][1])/gcd;
					X = (X % mod + mod) % mod;//保证最小解 
					nums[j][1] = nums[i][1] + X * nums[i][0];
					nums[j][0] = (nums[j][0] * nums[i][0]) /gcd;
					nums[j][1] = (nums[j][1] % nums[j][0] + nums[j][0]) % nums[j][0];//保证最小解 
				}	
			}
		}	
		if(flag == 1){
			flag = 0;
		}
		else{
			//将不与其他互质的组填入 
			a[ai][0] = nums[i][0];
			a[ai++][1] = nums[i][1];
		}
	}
		
	int  b[ai];//存放X1，X2...... 
	for(i = 0;i < ai;i++){
		j = i + 1;
		b[i] = 1;
		// 使b[i]存放a的数组中除a[i]以外所有乘积 ，类似题解中的 5 * 7  
		while(j % ai != i){
			b[i] *= a[j % ai][0];
			j++;
		}
		// 类似题解中的 (5 * 7 * N) %3 = 2   b[i]= X1 =5 * 7 * N = 35 
		int count = 2;
		int  fnum = b[i];
		while(count <= a[i][0]){
			if(fnum % a[i][0] == a[i][1])    break;
			else fnum = count++ * b[i];
		}
		b[i] = fnum;
	}
	long long X = 0;
	long long X1 = 1;
	for(i = 0;i < ai;i++){
		X += b[i];//X = X1+ X2+X3+...
		X1 *= a[i][0];// 所有除数的乘积 
	}
	long long minnum = X % X1;
	printf("%lld", minnum);   
	return 0;
}

拓展几种求最大公约数的方法

一、更相减损法

两个正整数a和b（a>b），它们的最大公约数等于a-b的差值c和较小数b的最大公约数。

二、辗转相除法（欧几里得算法）

两个正整数a和b（a>b），它们的最大公约数等于a除以b的余数c和b之间的最大公约数。

 

或

 

求最小公倍数的方法

最小公倍数就是它们的乘积再除以最大公约数

扩展欧几里得（扩展GCD）算法

详解扩展欧几里得算法（扩展GCD） - Seaway-Fu - 博客园 (cnblogs.com)

 代码中的x 就是之前同余子式中的k1

存在无解的情况，如

X = 1（mod 3）

X = 2（mod 6）

逆元

  给出 a 和 m ，一个数有逆元的充分必要条件是gcd(a,m)=1，此时逆元唯一存在，这时方程 ax ≡ 1（mod m）的最小整数解 x 称为 a 模 m 的逆元。

  逆元的含义：

    在模m意义下，一个数a如果有逆元x，那么除以a相当于乘x。

  为什么要有乘法逆元呢？

    当我们要求（a/b） mod p的值，且a很大，大到会溢出；或者说b很大，达到会爆精度。无法直接求得a/b的值时，我们就要用到乘法逆元。