Codeforces Round #643 1355E.Restorer Distance（三分/二分）

题目描述：

E. Restorer Distance

time limit per test 1 second

memory limit per test 256 megabytes

You have to restore the wall. The wall consists of N pillars of bricks, the height of the i-th pillar is initially equal to hi, the height is measured in number of bricks. After the restoration all the N pillars should have equal heights.

You are allowed the following operations:

put a brick on top of one pillar, the cost of this operation is A;
remove a brick from the top of one non-empty pillar, the cost of this operation is R;
move a brick from the top of one non-empty pillar to the top of another pillar, the cost of this operation is M.
You cannot create additional pillars or ignore some of pre-existing pillars even if their height becomes 0.

What is the minimal total cost of restoration, in other words, what is the minimal total cost to make all the pillars of equal height?

Input
The first line of input contains four integers N, A, R, M (1≤N≤105, 0≤A,R,M≤104) — the number of pillars and the costs of operations.

The second line contains N integers hi (0≤hi≤109) — initial heights of pillars.

Output
Print one integer — the minimal cost of restoration.

Examples
input

3 1 100 100
1 3 8

output

12

input

3 100 1 100
1 3 8

output

9

input

3 100 100 1
1 3 8

output

4

input

5 1 2 4
5 5 3 6 5

output

4

input

5 1 2 2
5 5 3 6 5

output

3

算法标签：三分/二分

题目大意：对于n堆石头，每堆高度为$h_i$，可以做三种操作：

1. 使某堆石头高度+1，代价为A
2. 使某堆石头高度-1，代价为R
3. 将一块石头从一堆搬到另一堆（一堆高度-1，另一堆高度+1），代价为M

问使得每堆石头的高度都相同的最小代价。

首先，如果$A+R<=M$，意味着搬石头的代价大于先加一块再减一块，因此直接令$M=min(M,A+B)$。

假设给定最终石堆的高度为H，计算出总共需要增加的石头数$up$，以及减去的石头数$down$（朴素思想复杂度为O(n))，分情况考虑up和down的大小关系，可以直接计算出总代价
$$c=\{\begin{array}{rlr}(down-up)\ast R+up\ast M& & (down>=up)\\ (up-down)\ast A+down\ast M& & (down<up)\end{array}$$

那么只要确定H与c的关系是一个存在最小值，且在最小值左、右侧分别具有单调性（类似于单谷函数），就可以用三分（或者二分判断增量）找到最小代价了，问题就在于怎么证明它有类似于单谷函数的单调性。

contest的时候当然凭感觉猜一下，或者通过打表之类的方法观察到了就可以直接开始写了，但是回过头看似乎很难想到一个直观且严谨的证明方法，所以这里就只能通过比较麻烦的数学计算来证明一下。

令$H^{\prime }=H+\Delta H$、$c^{\prime }=c+\Delta c$。我们来考虑当$\Delta H=1$时，c的增量$\Delta c$。只要能证明$\Delta c$在整个过程中是单调不递减的，就能证明$c$符合要求。

令高度小于$H^{\prime }$的石堆个数为$X$，那么$u{p}^{\prime }=up+X,dow{n}^{\prime }=down-(n-X)=down+X-n$。
为了计算$\Delta c$，我们先考虑$down>=up$且$dow{n}^{\prime }>=u{p}^{\prime }$的情况。
$\Delta c=c^{\prime }-c=(dow{n}^{\prime }-u{p}^{\prime })\ast R+u{p}^{\prime }\ast M-(down-up)\ast R-up\ast M$代入后计算得到$\Delta c=X\ast M-R\ast n$
同理，当$down<up$时$\Delta c=X\ast M-(M-A)\ast n$
也就是
$$\Delta c=\{\begin{array}{rlr}X\ast M-R\ast n& & down>=up\\ X\ast M-(M-A)\ast n& & down<up\end{array}$$
又因为$M=min(M,A+R)$，所以$(M-A)<=R$，当down<up时，$\Delta c>=X\ast M-R\ast n$
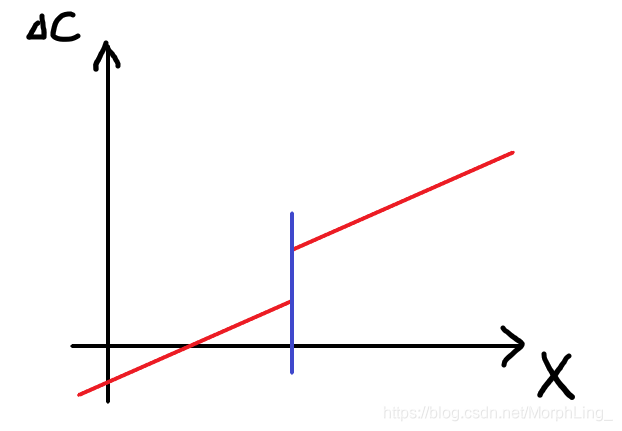
于是$\Delta c$与$X$的如图红线（断开来的地方就是down和up关系变化的点），满足单调不递减

然后问题在于证到这里现在只能说明$\Delta c$在两段上各自单调不递减，没有考虑到由down>=up变为down<up的那一次变化的增量。所以我们再把这种情况单独拿出来。

此时$c$用down>=up的情形计算，而$c^{\prime }$用down<up的情形计算，得到
$$\Delta c=X\ast M-(A+R-M)\ast (down-up)-n\ast (M-A)$$
我们需要证的是，

1. 若$\Delta c<0$则$X\ast M-n\ast R<=0$也成立（上一次变化也要<=0)；
2. 若$\Delta c>0$则$X\ast M-(M-A)\ast n>=0$也成立（下一次变化也要>=0)

（这里不要求$\Delta c$的单调性了，而只考虑它的正负）
（如果 $\Delta c=0$，c变化量为0，总是符合要求，不作考虑）
证明：

1. 由$down-up<=n$（否则$dow{n}^{\prime }<u{p}^{\prime }$不成立）得，
   $X\ast M-n\ast R=X\ast M-(A+R-M)\ast n-n\ast (M-A)<=\Delta c<0$

2. 由$A+R-M>=0，down-up>=0$得$(A+R-M)\ast (down-up)>=0$，
   因此$0<\Delta c<=X\ast M-(M-A)\ast n$

由以上两点，c在从$down>=up$到$down<up$ 这一步的变化中也能够维护极值两侧的单调性了。

这种证法可能看上去比较吃力，但是至少逻辑上说得通了。希望以后能找到别的更好的理解方法吧。

有了这个之后就符合三分或者二分的条件了。

贴一个二分高度判断增量+二分求代价的代码，复杂度 O(logNlogN)，（但是跟O(N)求代价的O(NlogN)算法跑下来时间差不多）通过判断当前位置mid和mid+1所需代价的关系，即可确定mid在极值左侧还是极值右侧。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
 
const int N=2e5+5;
int n,a,r,m,mid;
ll sum[N],h[N];
 
ll cal(ll x)
{
    ll down=0,up=0,ret=0;
    int pos=lower_bound(h+1,h+1+n,x)-h;
    if (pos>=1)up+=(pos-1)*x-sum[pos-1];
    if (pos<=n)down+=(sum[n]-sum[pos-1])-(n-pos+1)*x;
    if (up>down) ret+=(up-down)*a,up=down;
    else
        ret+=(down-up)*r,down=up;
    ret+=up*min(a+r,m);
    return ret;
}
int main()
{
    cin>>n>>a>>r>>m;
    for (int i=1;i<=n;i++)
        scanf("%lld",&h[i]);
    sort(h+1,h+1+n);
    for (int i=1;i<=n;i++)
        sum[i]=sum[i-1]+h[i];
    int l=0,r=1e9;
    while(r-l>1)
    {
        mid=(l+r)>>1;
        if (cal(mid)>cal(mid+1))
            l=mid;
        else
            r=mid;
    }
    printf("%lld",min(cal(l),cal(r)));
    return 0;
}