图形和数值的数据集描述方法

图形方法对数据集的描述

1. 条形图（bar graph）

条形图一般横向表示类别（class），纵向表示该类别所对应的类别频率（class frequency）。
2. 饼状图（pie graph）

饼状图是一个圆周，每个类别对应的扇形面积大小和类别相对频率（class relative frequency）成比例。
3. 帕累托直方图（pareto diagram）

帕累托直方图是讲直方图按照从高到低的顺序排列之后所形成的直方图。

---

以上三种图形表示方法是定性数据描述中常用的方法，在定量数据集描述中，还有以下的图表描述方法。

---

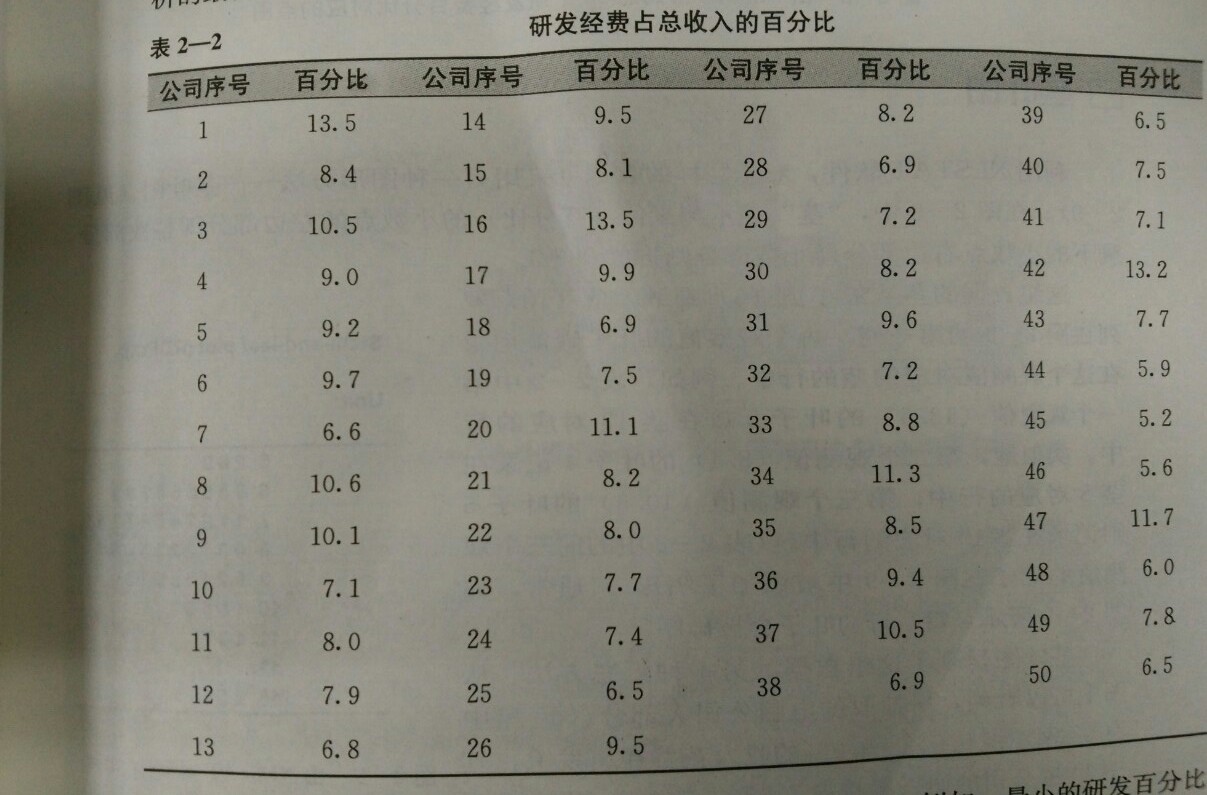
根据上表数据可以得到下图：
4.点图（dot plot）

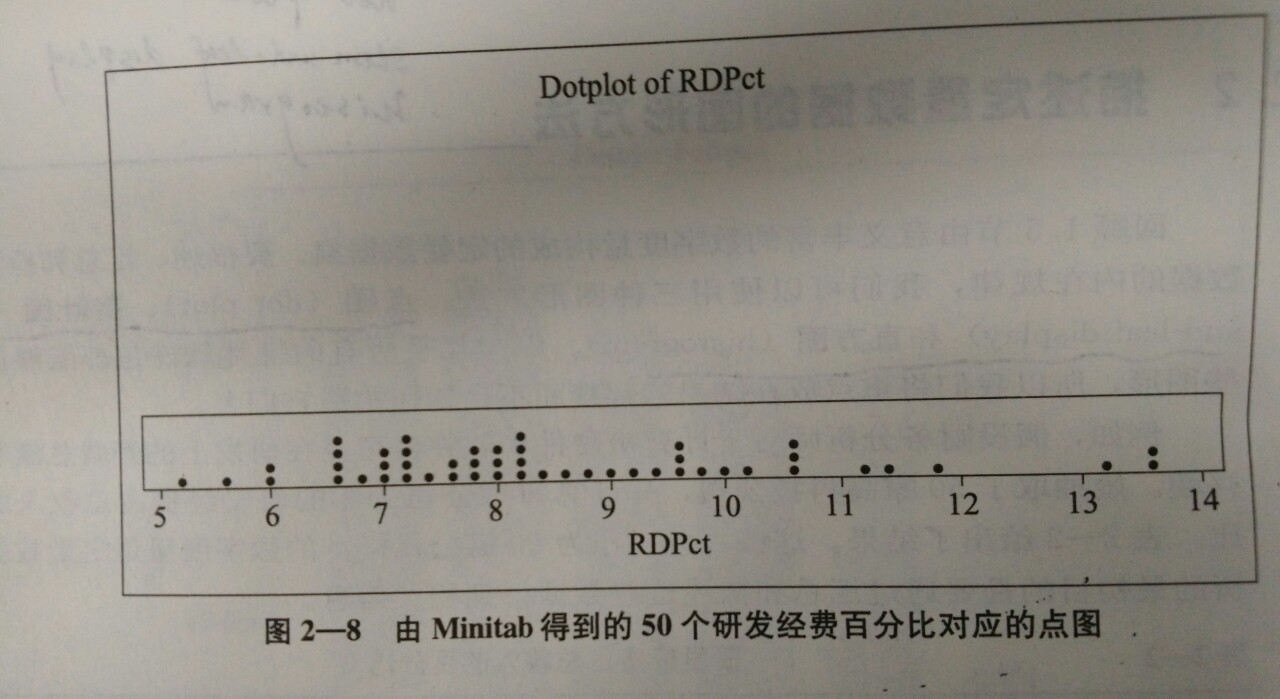
每个观察值放在横轴上，当有重复的观察值时，则放在这个点上面，于是堆积成了此图。
5. 茎叶图（stem-and-leaf display)

将观测值百分比分为两部分，小数点左边的数字作为“茎”，小数点右边的数字作为“叶”。
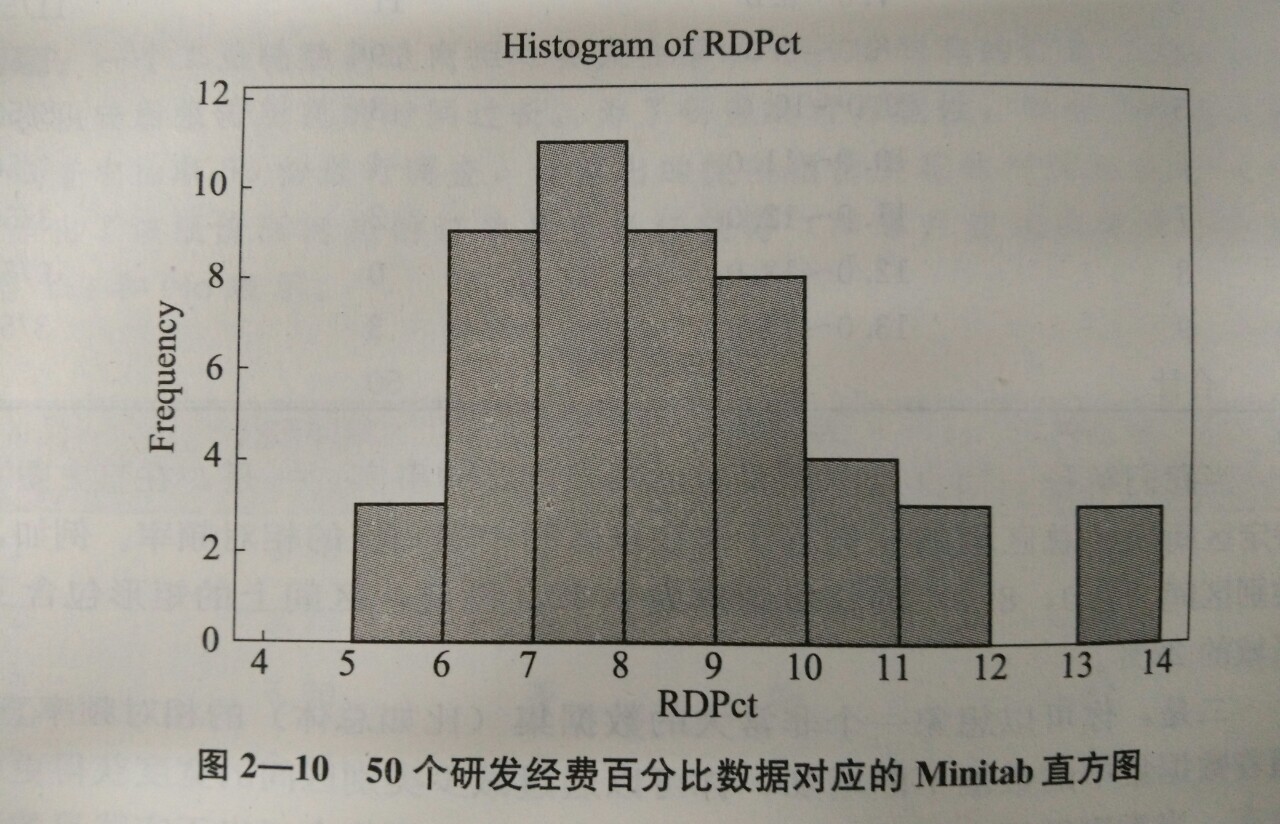
6. 直方图

直方图是对横轴数值进行区间划分。

---

4-6是常用的定量数据集的图形描述方法，这三种方法各有所长，最大的优点可以看出数据主要集中在那个范围之内。

---

7. 箱线图（box plot）

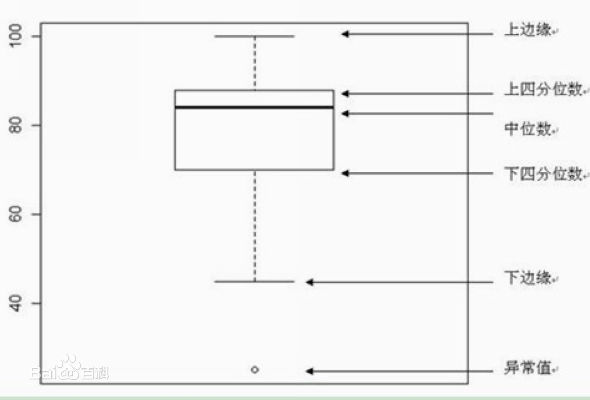
箱线图一般用于异常值的检测，是基于四分位差（interquartile range，IQR）建立的。四分位差是指上四分位数($Q_u$)和下四分位数($Q_i$)之间的距离，即

$$IQR=Q_u-Q_i。$$
箱线图中：

下内栏=