DC3算法是什么
DC3算法(也称为Skew算法)是一种高效的构建后缀数组的算法,全称为Difference Cover Modulo 3算法。
该算法于2002年被提出,论文参考:
https://www.cs.cmu.edu/~guyb/paralg/papers/KarkkainenSanders03.pdf
后缀树的引入
后缀数组是什么
后缀数组是一个整数数组,用来表示某个字符串所有后缀在字典序中的排序。
- sa数组
后缀数组又称为sa数组(Suffix Array),其元素表示原字符串各后缀在字典序中的位置排序。
如果字符串S的后缀树组为sa,那么sa[i] 表示S中第i小的后缀在原字符串中的起始位置。
- rank数组
与sa数组对应的是rank数组,它表示每个位置上的后缀在后缀数组中的排名。
如果字符串S的后缀树组为sa,那么rank[i]表示以i口头的后缀在后缀数组中的排名。
- 两者关系
根据上面的定义,我们可以知道,rank数组是sa数组的逆数组,也即是:
rank[sa[i]] = i,sa[rank[i]] = i
我们通过 banana 这个字符串来演示 sa数组 以及 rank数组的工作原理
- step1:构建所有后缀并按字典顺序排序
列出 “banana” 的所有后缀
0: banana
1: anana
2: nana
3: ana
4: na
5: a
按字典顺序排序后
5: a
3: ana
1: anana
0: banana
4: na
2: nana
- step 2: 构建后缀数组 SA 和 rank 数组
根据排序结果,构建sa数组 :
SA = [5, 3, 1, 0, 4, 2]
构建 rank 数组:
rank[5] = 0
rank[3] = 1
rank[1] = 2
rank[0] = 3
rank[4] = 4
rank[2] = 5
因此 rank数组为:
rank = [3, 2, 5, 1, 4, 0]
再来看一个例子

能解决什么
后缀数组+rank数组 可以接解决非常多的字符串问题
还能去做RMQ问题,也即是Range Maximum/Minimum Query 的缩写,表示区间最大(最小)值
关键点在于后缀数组怎么样形成最方便
后缀数组的地位
它的地位非常高, 很多的问题都是由 后缀树 或 后缀数组 实现的
后缀树 实现 跟后缀数组实现的区别
后缀数组可以替代非常多后缀树的内容
因为后缀树生成是更麻烦的一个东西
我们用后缀数组可以代表字符串的一些后缀信息, 可以解决很多字符串的问题
后缀树案例说明
后缀字符串
从开头开始往后所有都要
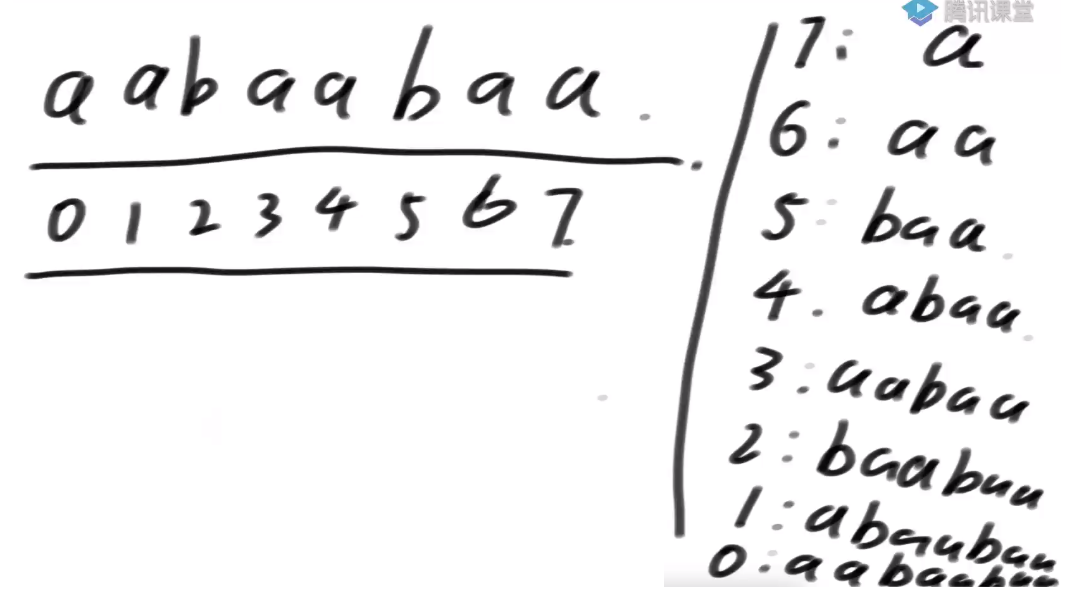
对所有后缀字符串做典序排序
所谓的后缀数组它其实代表所有的后缀字符串在排完名之后,从第0名到第7名依次写下来,这就是所谓的后缀数组

注意一点:不会有排名相同的,因为所有后缀串的长度不同
怎么样生成排名
先看一下暴力方法生成的流程
- step1:先生成所有的后缀字符串, 复杂度O(N^2)
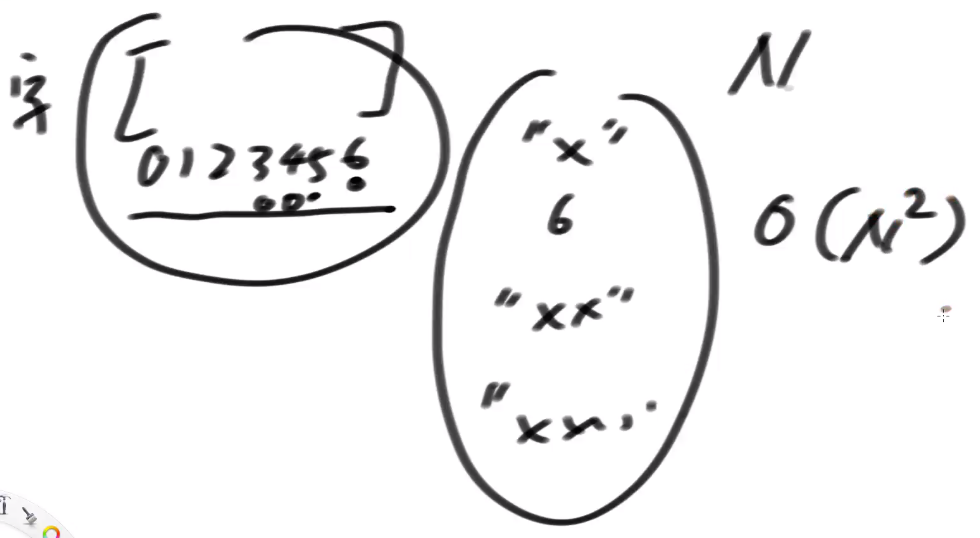
- step2:后缀字符串数量 O(N), N个后缀字符串排序, 代价O(N*logN)
两个字符串比较大小的复杂度是O(1)吗? ==> 和字符串的长度有关,后缀串的平均长度O(N)
暴力生成的复杂度
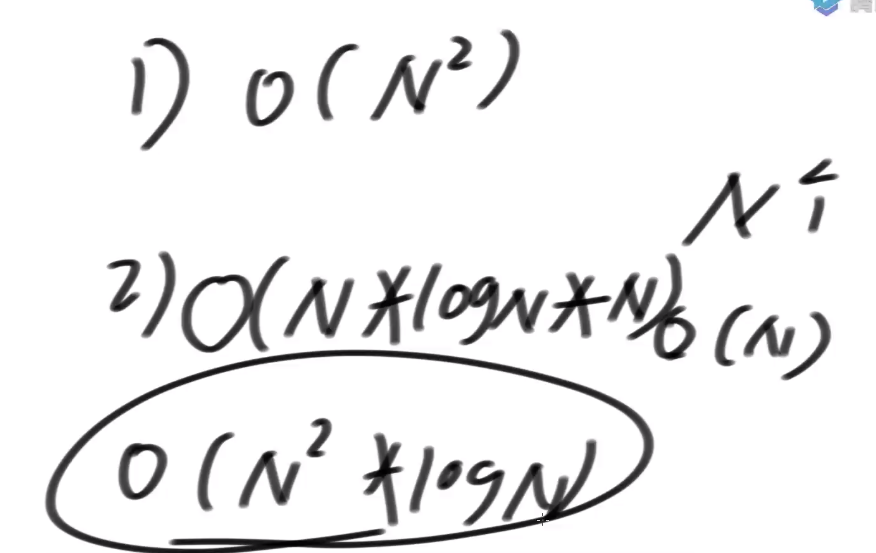
暴力方法生成后缀数组
- 生成所有的后缀串
光生成后缀数组的字符串数组代价就已经是O(N^2)了
后缀字符串的数量是O(N)的
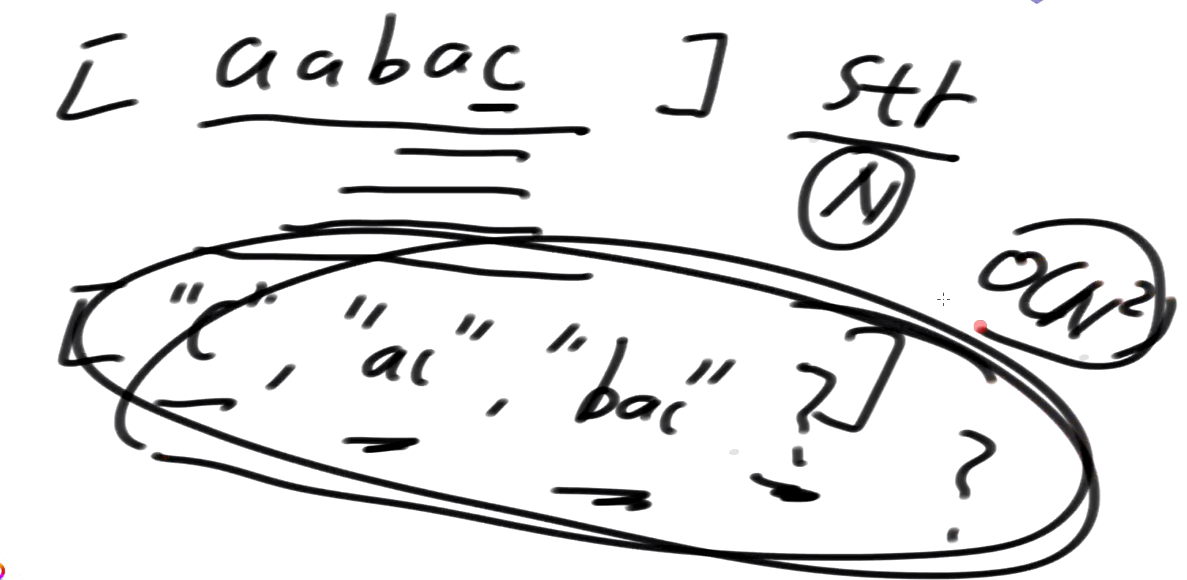
- 给定长度为N的字符串
1)生成所有后缀数组的字符串数组, 复杂度O(N^2), 也是N

2)排序, N*logN, 但问题是这里的排序是两个字符串直接比较大小
字符串的平均长度是N/2
把字符串数组排好序, 单个两个字符串比对的代价O(N)
字符串排序的代价是O(N^2*logN)
是一个很痛的瓶颈

DC3算法引入
上面暴力方法说明生成后缀树时,字符串间的字典序比较是一个耗时操作,我们需要寻求是否有一种算法来优化这一部分内容。
于是DC3算法应运而生,它能够做到时间复杂度为 O(N) 解决上面的问题。
其核心思想:根据下标模3来分组, 做了一个类似于递归的事情来把这个问题解决的。
后缀数组的复杂度跟要求
后缀数组可以做到生成复杂度: O(N)
但是有一个前提:初始时, 数组里头每一个的值不要太大
如果非常大, 下面的方法就不合适了, 常数项就会有点大
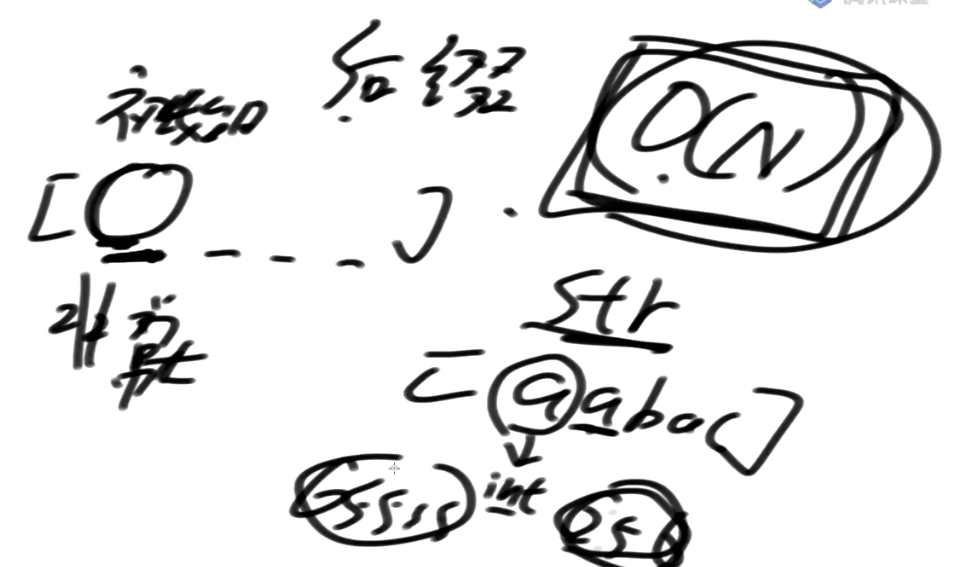
回顾:基数排序
比如所有的数字都是三位
- step1:先按照个位数进桶
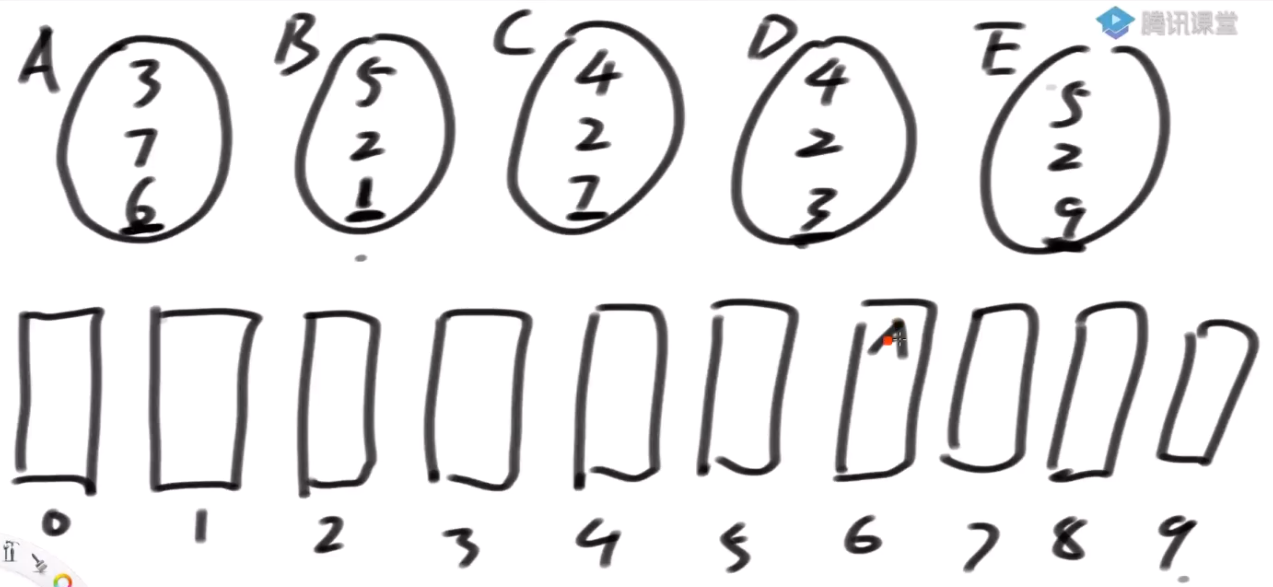
-
step2:从 0~9 顺序从桶中拿出数字来,然后按照十位数字进桶,后进的权重更大
-
step3:重复step2,直到最高位
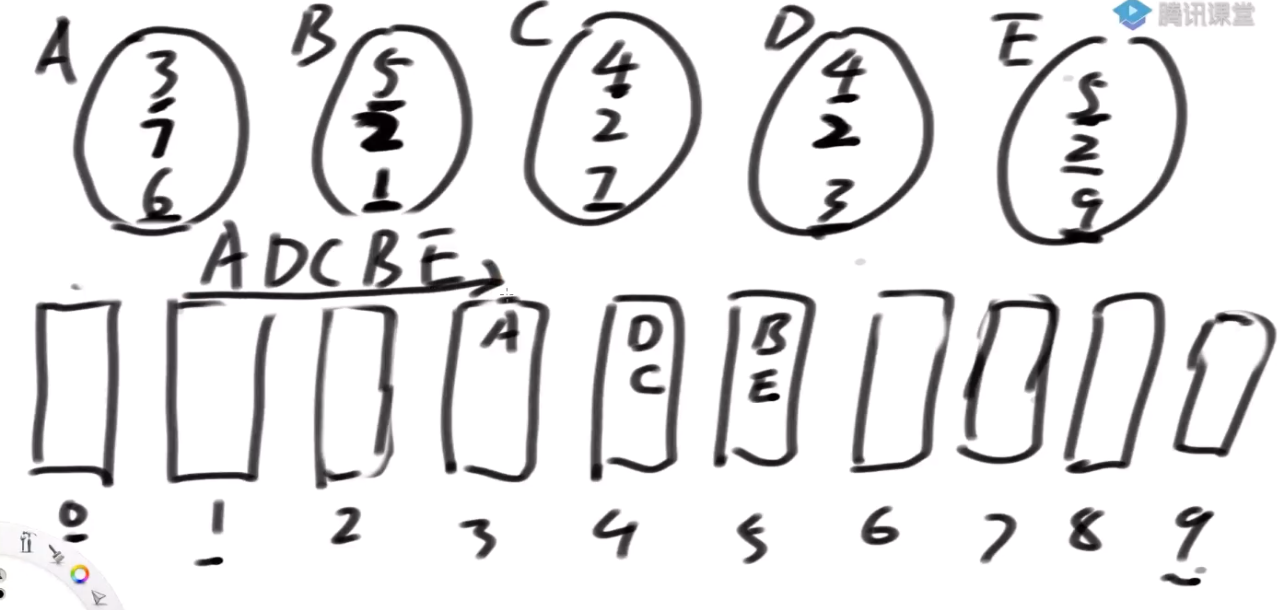
这里我们可以做一个升级, 有两位数据, 每一个数据有两个指标
56, 4 : 56 算一位, 不要拆开
对上面数据排序
3-7 最前 17-79 第二 23-34第三位 最后56-4
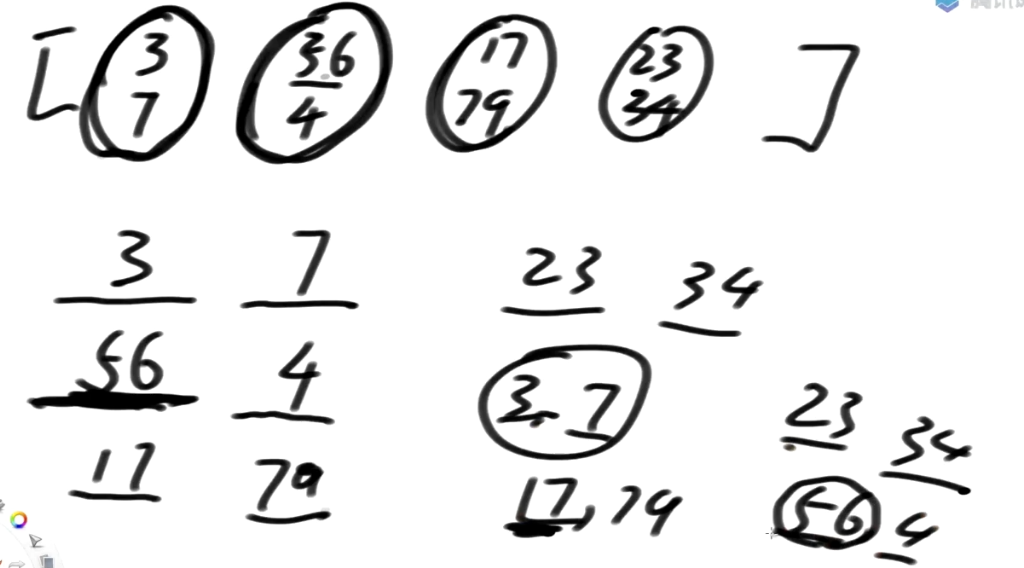
如果N个样本, 数据的维度不超过3维, 而且每个维度的值相对较小(比如1000以内),否则基数排序的常数项极大
则N个样本排序的代价可以做到O(N)
如果一个数据有3维信息, 每个位置的值不会特别大的话,
如果有N个数据, 排完序的代价还是O(N)的
前提是每一位上的值不要太大
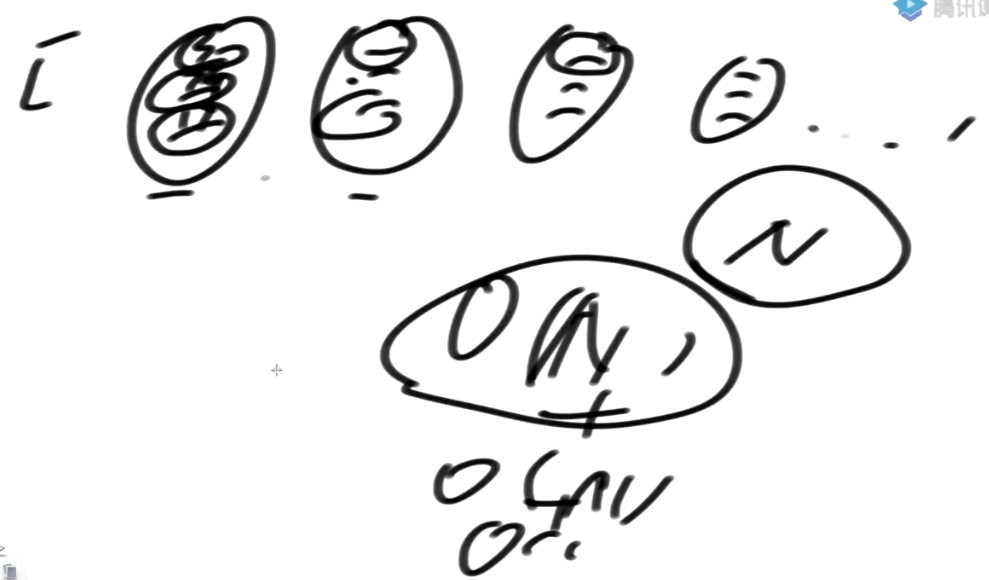
再谈后缀树组
把字符串可以认为是一个数组, 每个位数据是这个字符串的ASCII码
=>可以把一个字符串求后缀数组,等同于对一个数组在求后缀数组。
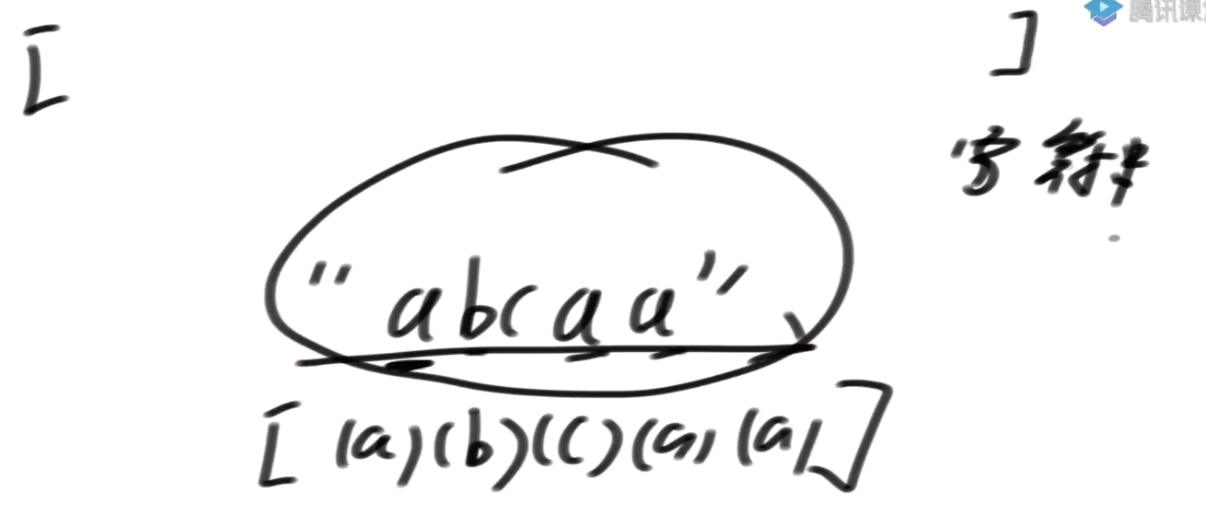
所以字符串可以求后缀数组,对于单独数组来说也可以求后缀数组
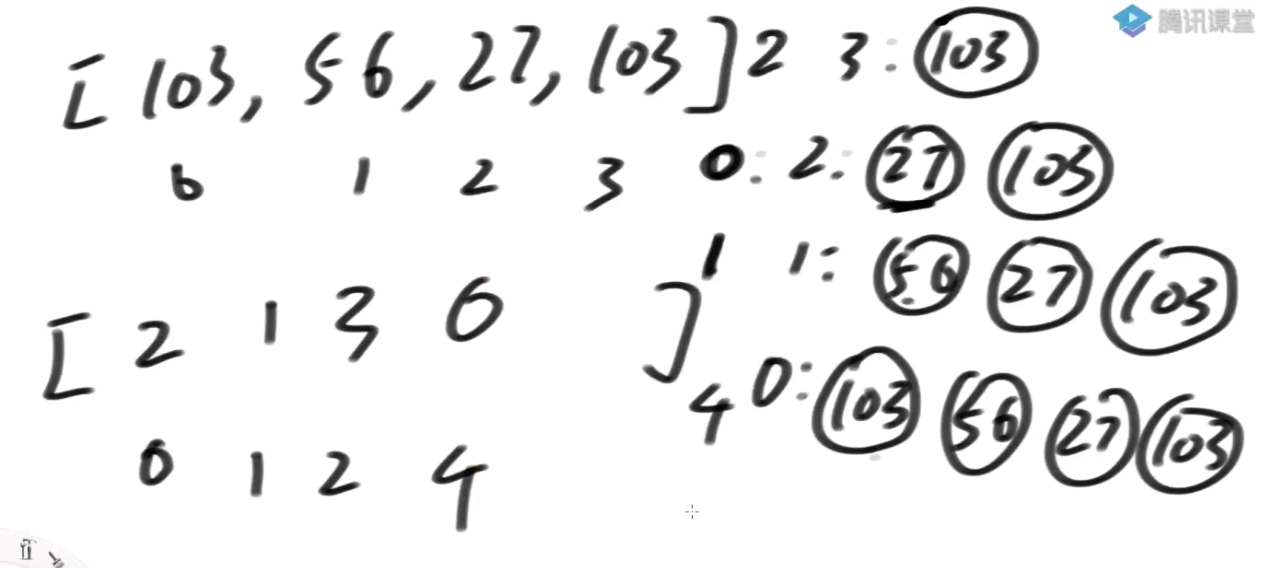
背景介绍
比赛中常用的后缀数组生成算法,时间复杂度最优的解是DC3算法,复杂度为O(N)
但是由于后缀数组一般耗时很久,所以比赛中的测试数据不会给的很高,选手也常用倍增算法解决, 它的复杂度为O(NlogN), 但是常数项优秀(从上面的介绍中可以看到,DC3算法使用了基数排序,常数项其实是很差的)。
扯得有点远,我们说回到 DC3算法。
DC3算法思路
下标分类
- 首先, 按 索引对3取模 做下标分类
i%3== 0 ==> 0类下标, 代号s0类
i%3== 1 ==> 1类下标, 代号s1类
i%3== 2 ==> 2类下标, 代号s2类
所有后缀字符串, 长度不一样, 所以不会有后缀串排名一样

S12推出S0内部排名
假设有一个非常方便的方法 先把S1, S2类的后缀数组排名求出来(后面展开,这里先把S12当做一个可以使用的黑盒)
我们能不能得出所有0类, 1类, 2类下标的整体排名?
所有3类混在一起的下标排名能不能通过S1, S2类的已经出来的信息,给它都加工出来?
怎么使用S1,2类的信息呢?
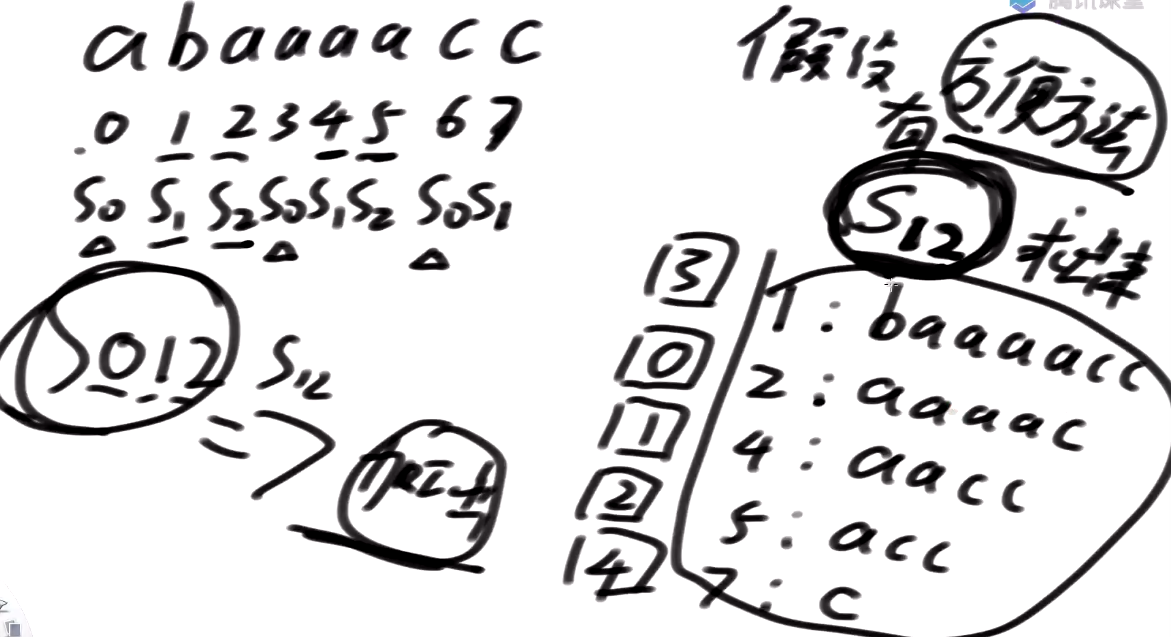
先看看S12类能不能把S0内部的排名搞定
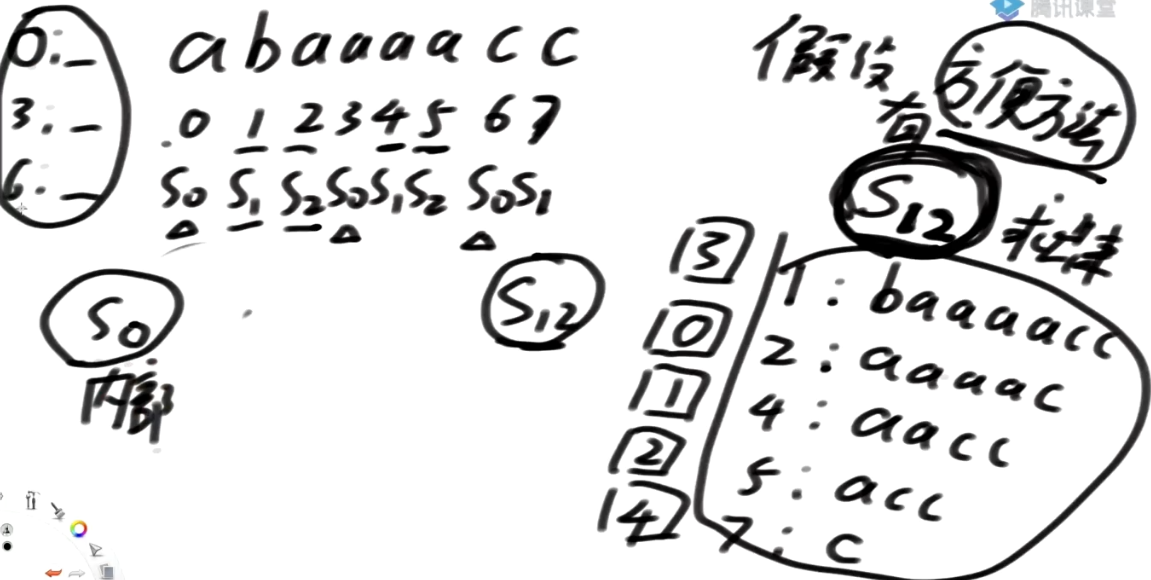
字符串不相同的情况
-
0开头的a
-
3开头的a
-
6开头的c
如果只看一个字符, 6的排名是不如0,3的
这个过程可以用基数排序
s0内部的首字母不一样, 根据首字母就可以划块了
首字母不一样的块之间的排名, 我一定能求出顺序
下面的问题就是0,3开头,这些同样在一个块内部的这些后缀串怎么排名?
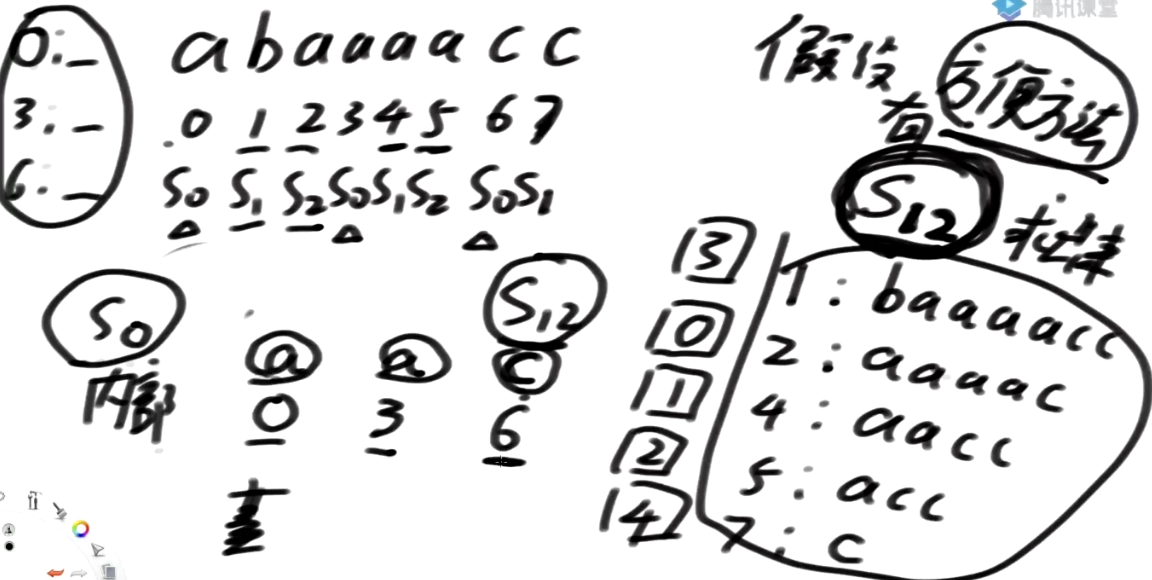
-
0开头的字符是a,后面的是1开头及其后面所有,S12中1开头的排第3位,因此S0中记为
a_3 -
3开头的字符也是a,后面的是4开头及其后面所有,S12中4开头的排第1位,因此S0中记为
a_1
在S12中:1开头及其后面的所有 跟 4开头及其后面的所有的总排名我们是知道的
虽然第一维数据一样, 但是0开头的 a_3 是干不过3开头的 a_1
依然可以基数排序, 过一遍决定顺序, 时间复杂度O(S0的大小),也即O(N/3)=O(N)
还是基数排序, 相当于一个对象 两位的信息
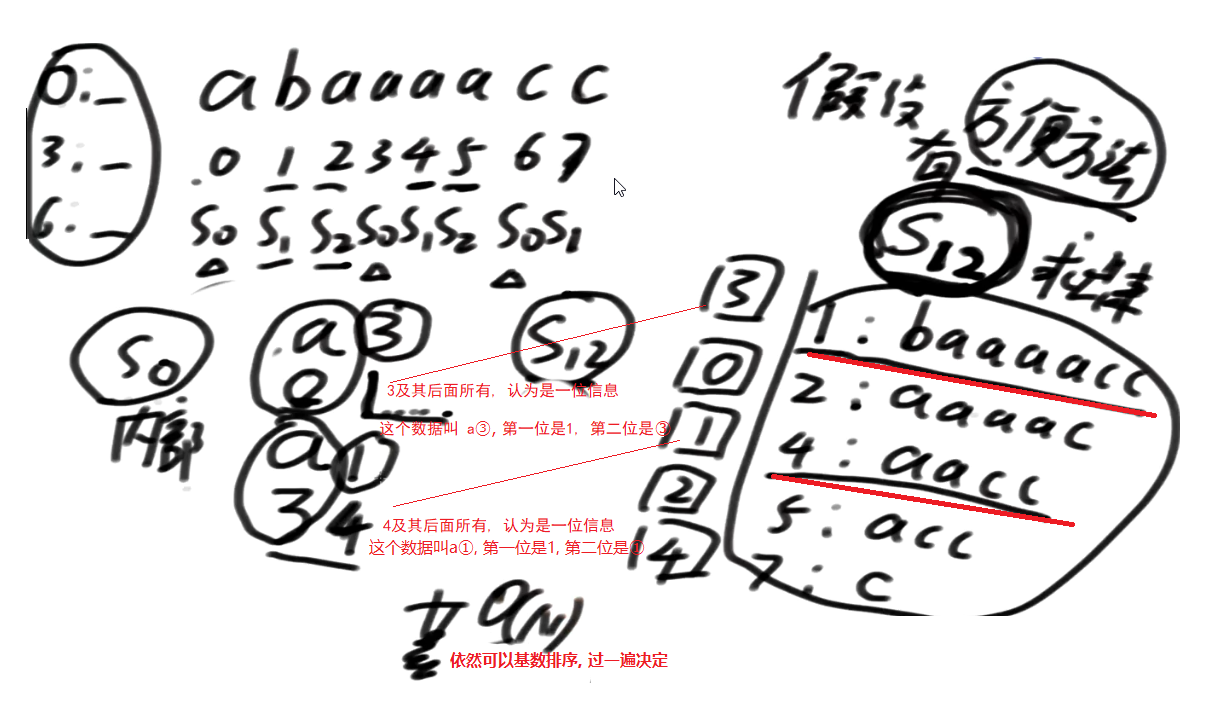
S12与S0的Merge
由上面的推导可以知道,如果已知S12,那么可以在O(N)的时间复杂度内推出S0。
接下来,自然而然地想到,如果需要得到整体排名,我们只需要得到 S12与S0的merge策略。
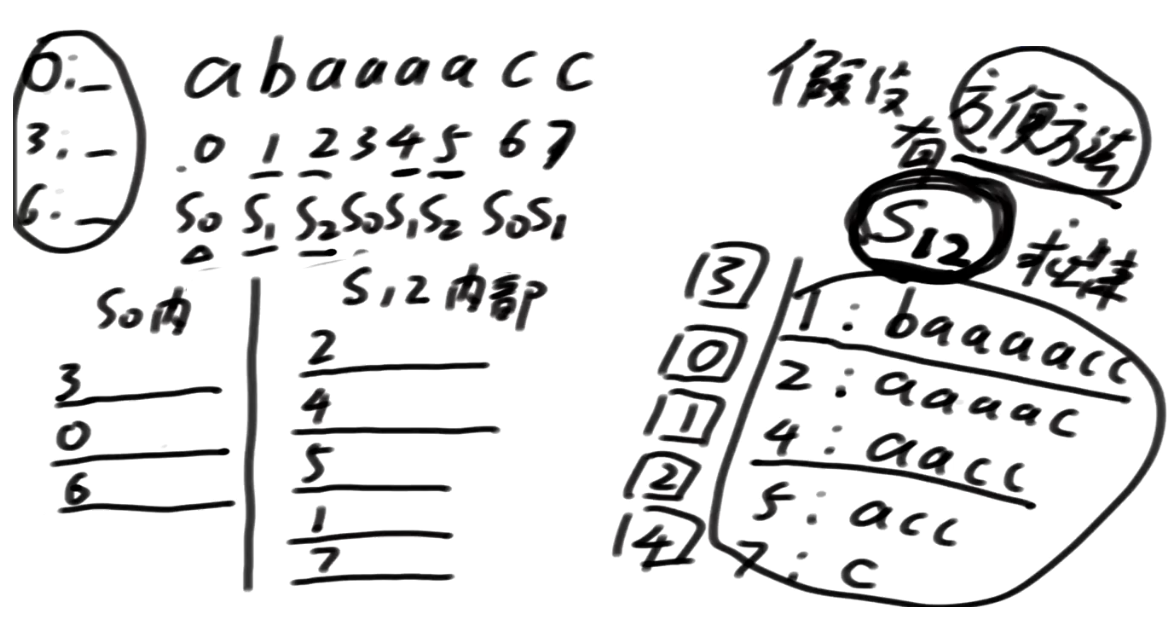
3 开头的 跟 2开头的谁小谁排出
依次从上往下, 如果我们存在merge策略
总排名就出来了
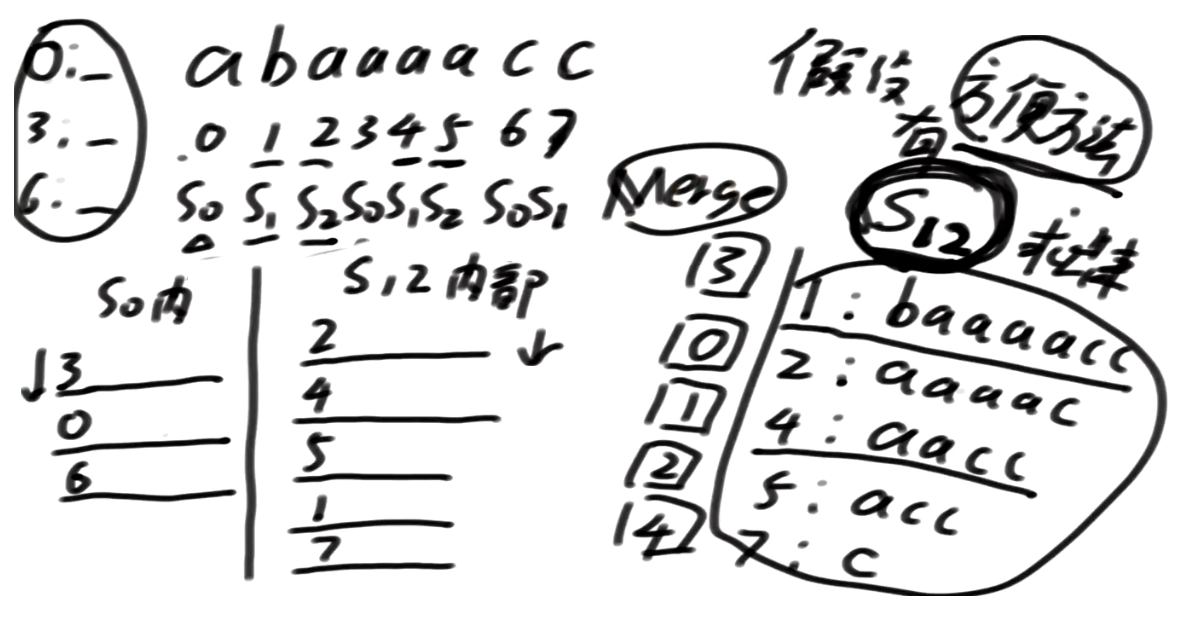
怎么进行merge呢?
我们先整体审视一变,同常规的 归并排序,或者说 map-reduce的reduce过程类似,由于S0以及S12都是有序的,我们只需要在S0以及S12侧都给到一个指针(表示在S0以及S12中数组的索引),逐一比较大小即可。
不妨设S0此时指针来到 p0,S12指针此时来到p12,如果p0指向的索引开头的字符以及p1指向的索引开头的字符不同则直接可以比较大小,我们不用进行后面的操作了。
如果 p0 以及 p12 指向的索引对应的字符相同,我们需要分情况讨论:
-
1)假设p12此时指向的是S1,例如 p0 此时指向6,p12此时指向10,那么只需要再向后看一位就一定可以知道排序,由于p0后面一位的字符为第7位以及后面所有的字符,而p12后面一位的字符为第11位以及后面所有的字符,我们知道 7和11的位置都在S12中,而S12的总体排序又是知道的,那么直接判断即可。
-
2)假设p12此时指向的是S2,例如 p0 此时指向6,p12此时指向11,那么只需要最多再向后看两位就一定可以知道排序,由于p0后面一位的字符为第7位以及后面所有的字符,而p12后面一位的字符为第12位以及后面所有的字符,如果第7位以及第12位字符不同,那么第6位以及第11位的后缀数组的字典序也必就能比较出来,如果还是相同,由于7在S12,而12在S0,不能直接比较,但是再往后看一位,6后面的第二位为8,11后面的第二位为13,8和13的位置都在S12,可以直接比较,那么6和11的顺序也就出来了。
总结一下:
-
如果p0以及p12指向索引的字符不同,直接出结果
-
如果p0以及p12指向索引的字符相同
-
p12位置为S1,再向后看一位出结果,加上当前位,也就是最多看2位就能出结果
-
p12位置为S2,最多再向后看两位出结果,加上当前位,也就是最多看3位就能出结果
-
也就是 merge 中每一步的比较时间都是 O(1) 的
下面还是看上面的具体案例
一开始 3 开头的 跟 2开头的 pk
- 3开头的上面字符是a
= 2开头的上面字符也是a
所以要再往下比较, 都是a, 又比不出来
再往下
-
考察5及其后面的整体
-
和4及其后面的整体
这俩排名在s12里有 ==> 最多三维信息可以搞定merge,只用比三个位置的信息就可以决定3开头跟2开头谁大谁小
这都不是基数排序,就三个位置的值比较一下
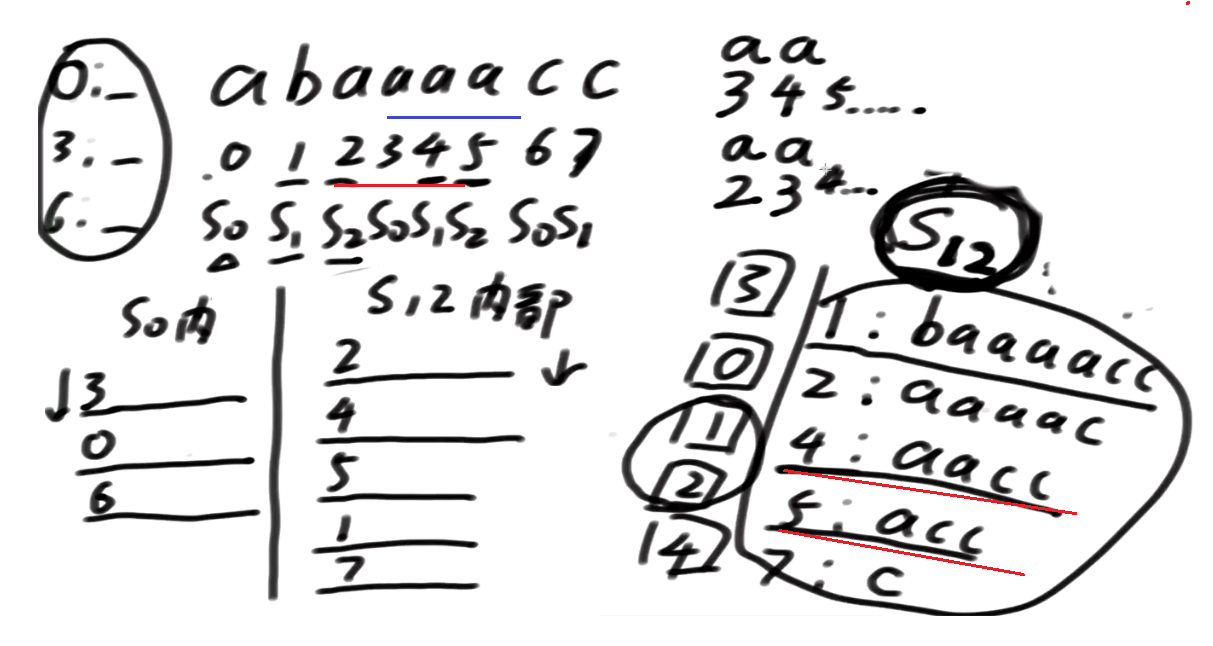
3是一个s0类的下标, 遭遇的是2 s2类的下标
当S0类下标在merge的时候遭遇了S2类下标跟它pk的时候, 往后要比三位
S0 跟 S2下标pk的时候, 最多拿三个位置的数比一下, 就知道怎么merge了, 谁大谁小就出来了
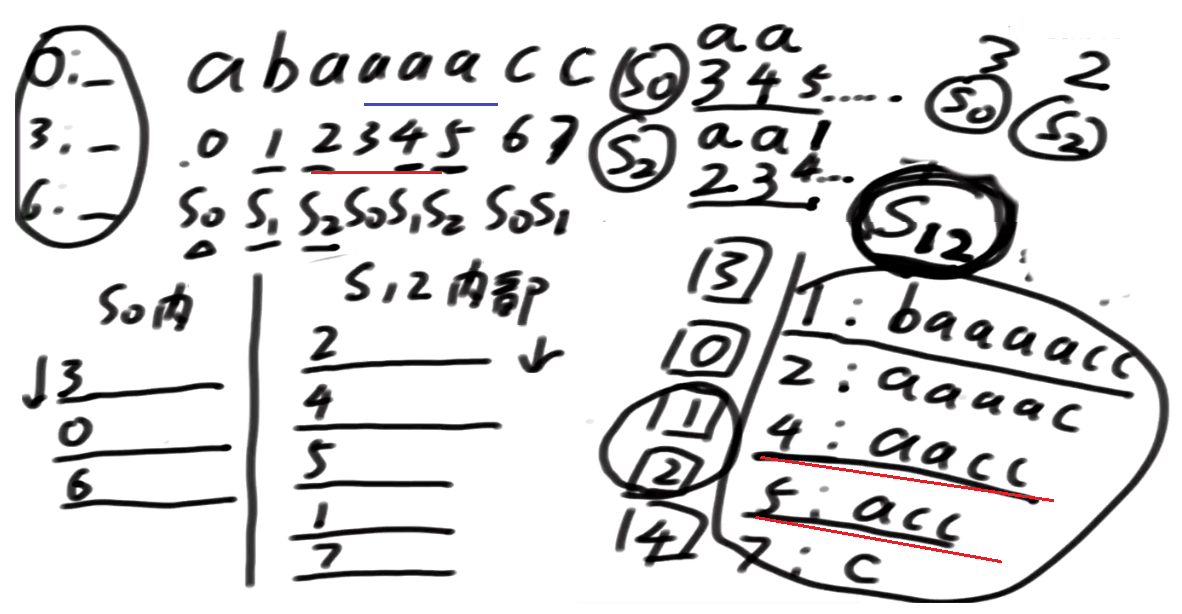
后面的信息, 3开头的是 2, 2开头的是1, 3开头的没pk过2开头的
2开头的就是所有下标开头的Number0
接下来3开头的跟4开头的pk
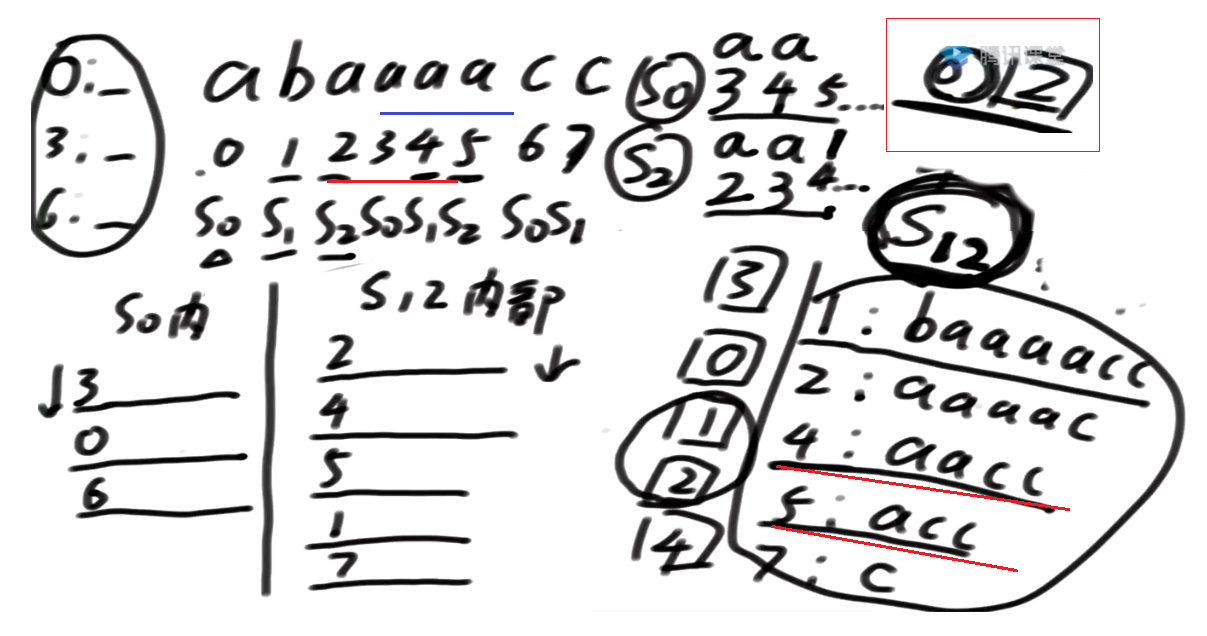
怎么样pk3开头的跟4开头的?
-
3开头的是s0类型
-
4开头的是s1类型
当S0类 跟 S1类下标pk的时候, 最多比两个位置的数
3位置是a, 4位置也是a
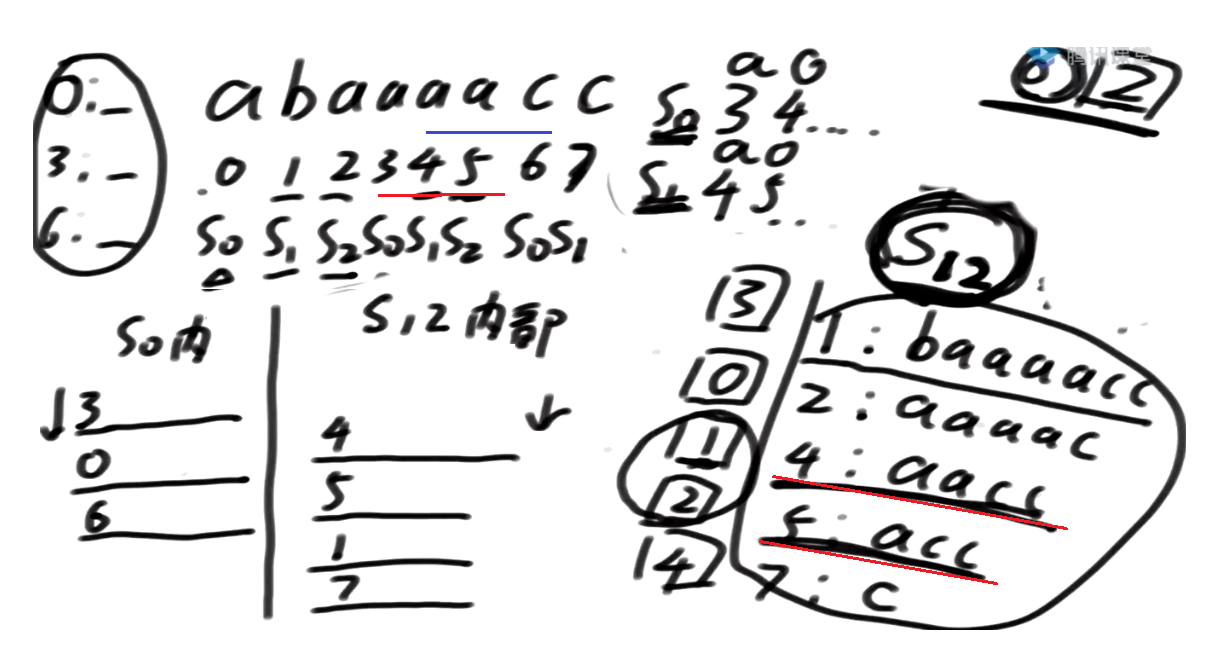
接下来比4及其后面的整体 和 5及其后面的整体
这俩排名在s12内部的排名是有的
所以S0类 跟 S1类下标pk, 最多比两个位置的数, 可以决定大小
DC3算法实现
总体流程
首先字符串长度N
-
step1:有一个f()函数 帮我得到S12内部的排名
-
step2:用s12 的信息得到s0内部的排名
- 使用基数排序: O(N)
-
step3:把S0 跟 S12去merge, 又利用到s12类的信息, 都排出来,时间复杂度: O(N)
step2以及step3的求解过程上面已经说明了,后面就不赘述了
可以看到, 整个流程中成败的关键就是第一步, 后面两个过程都是O(N)的过程
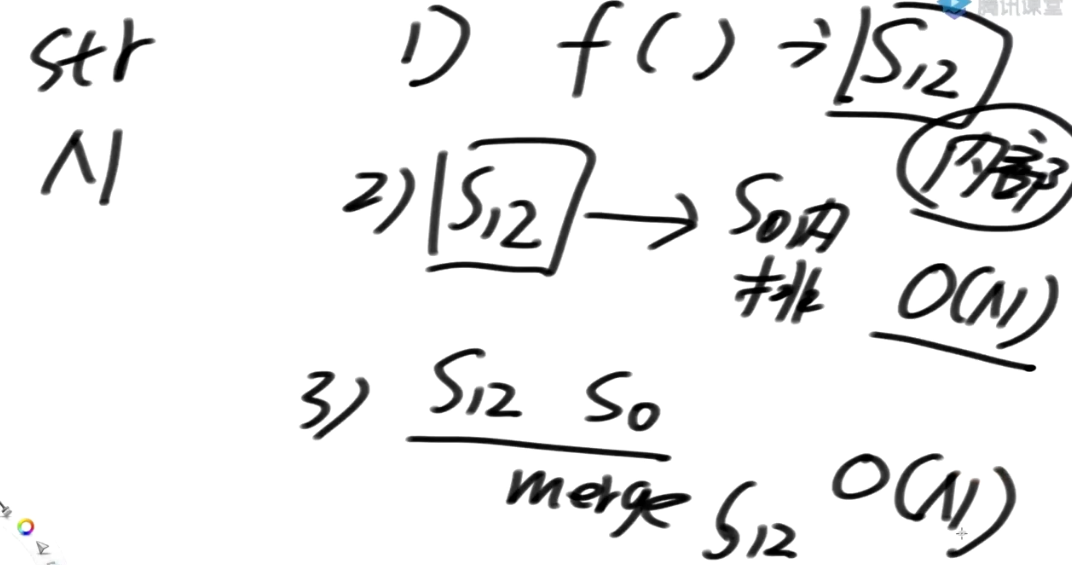
如何得到S12类的排名
处理流程
要求这个排名一定要是精确的,里面不要有重复值
画下划线的就是s12类
先这么想,怎么决出下面的整体排名
-
1开头及其后面的所有
-
2开头及其后面的所有
-
4开头及其后面的所有
-
5开头及其后面的所有
-
7开头及其后面的所有
-
8开头及其后面的所有
-
10开头及其后面的所有
-
11开头及其后面的所有
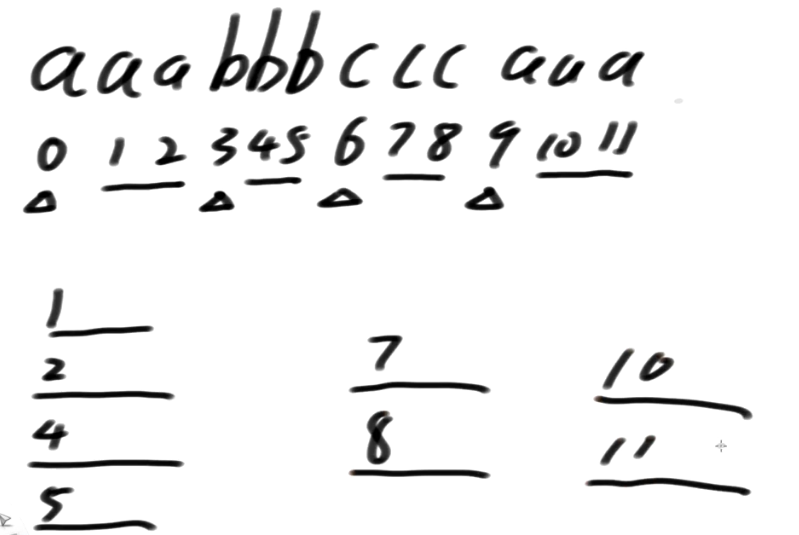
先只拿前三维信息做比较,如果此时字符不够3位了,用极小值来填充
-
1开头前三个字符aab
-
2开头前三个字符abb
-
4开头前三个字符bbc
-
5开头前三个字符bcc
-
7开头前三个字符cca
-
8开头前三个字符caa
-
10开头前三个字符aa0
-
11开头前三个字符a00
这个例子展示的是:如果我们仅拿3位信息就足以得到严格排名的话, 那岂不爽哉
那么这样的话只需要经过一个O(N)的基数排序就拿到S12了,接下来可以直接去做后面2,3的步骤
现实情况是: 有可能只拿前三位信息它排不出严格的排名
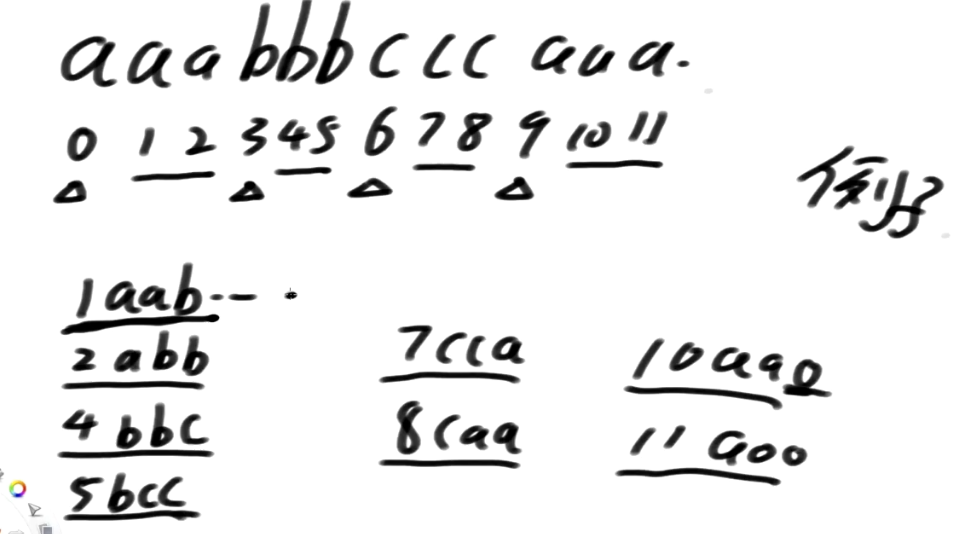
我们拿mississippi这个单词来做说明(注:这个是DC3论文中作者的提过的案例)
只拿1,2类信息的前3维信息 能不能得出精确排名呢?答案是不行滴 o(╥﹏╥)o
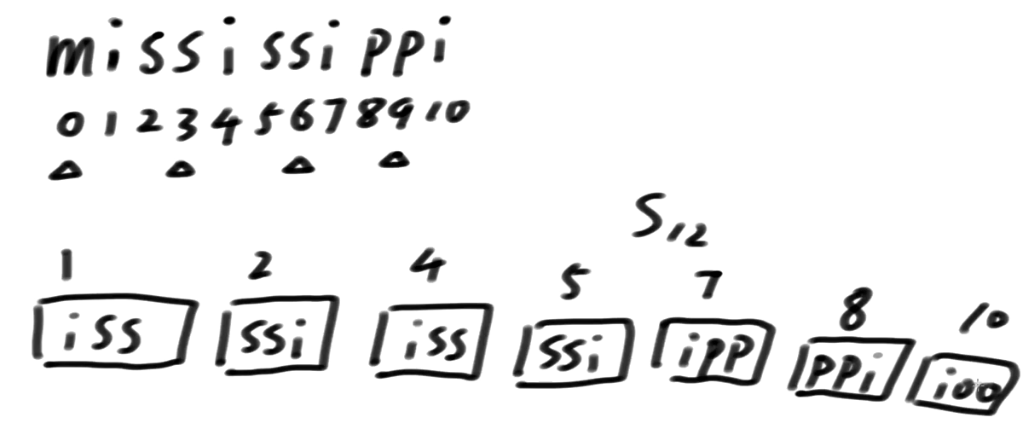
这样的话, 我们就没有决出精确排名
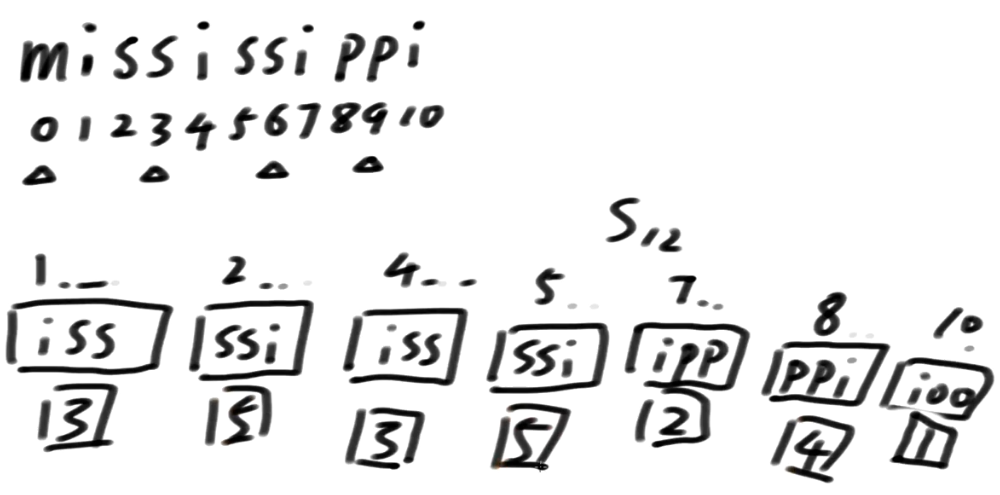
好了,整个算法中最精髓的部分,它来了!!!
生成一个数组:
-
把S1类整体放在数组左边
- S1类所对应的排名放数组左边
-
把S2类全放在数组右边
- S2类所对应的排名放数组右边
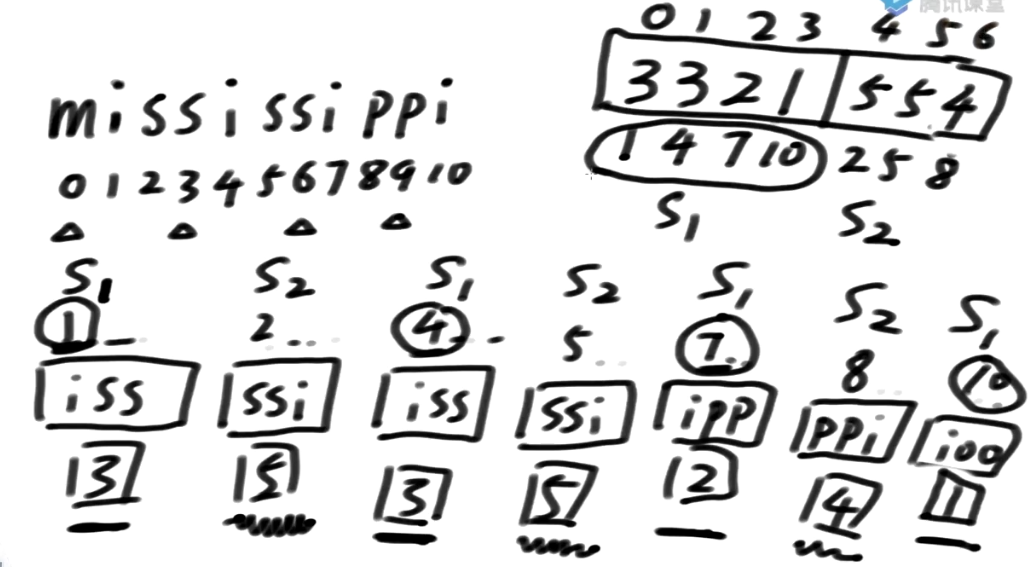
获取结果
我们把这个数据认为是个字符串数组,递归的调用求它后缀数组的排名
求出来了哪个是第一名?
1554, 3位置是第一名, 对应会原数组中10 它是第一名
下面是2开头的 21554, 对应会原数组中7 它是第二名
接下来是321…, 是原数组第1位置
接下来是3321…, 是原数组第0位置
接下来是4, 是原数组第6位置
接下来是54, 是原数组第5位置
接下来是554, 是原数组第4位置
后缀数组的这个结论求出来以后, 它可以对应回原来我想求这个东西里面的s12类的排名!!!
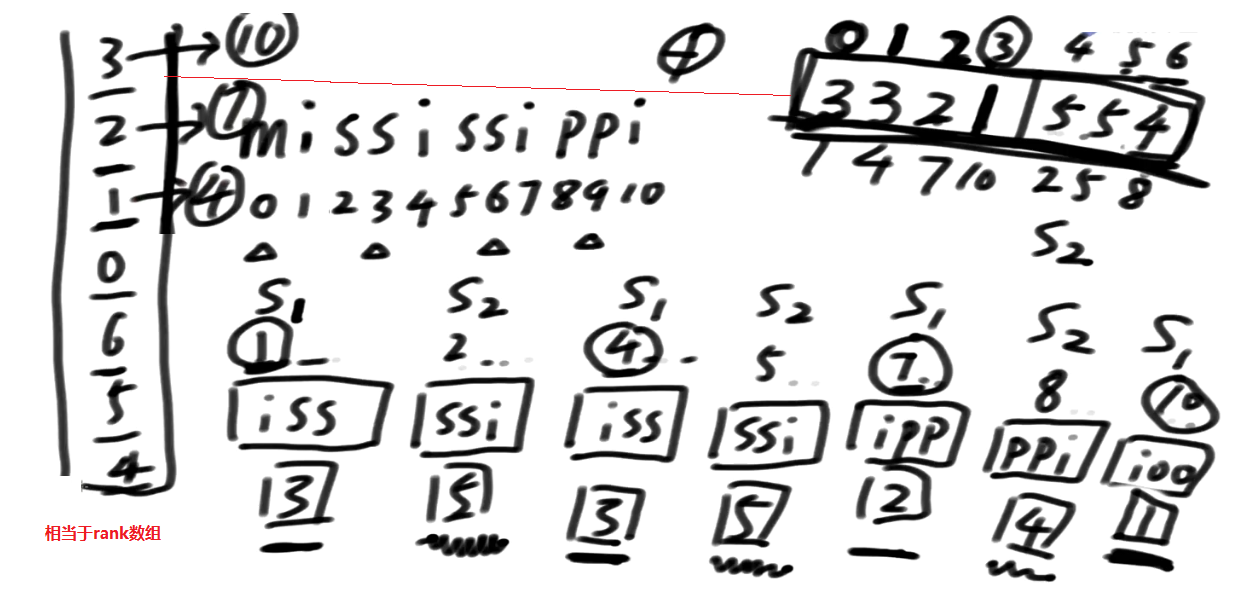
结论解释
一开始有一个比较粗糙的排名, 没有得到精确的排名,比如说 有两个3, 两个5
如果你把这个排名的值当做是字符的话, 我这个1不可能在排完字符串之后排名往后掉
相当于我首字母就是1,首字母如果划分出块了, 即便后面怎么摆, 也不会让排名乱掉, 块与块之间排名不会乱掉
为什么要这么摆?这么摆可以把同一块内部的排名搞定!
先看两个相同索引同时落在S1或者同时落在S2的情况
看这个两个3
3: 1开头及其后面的所有
3: 4开头及其后面的所有
分不出来
因为我们只拿了前3位信息出来, 它们彻底相等, 所以区分不出来
接下来, 你需要什么信息?
3: 123 4开头及其后面的所有
3: 456 7开头及其后面的所有
s1类摆在整体左边, s2类摆在整体右边
对于同一组内部, 这么摆, 正好这个结构关系能帮它区分排名
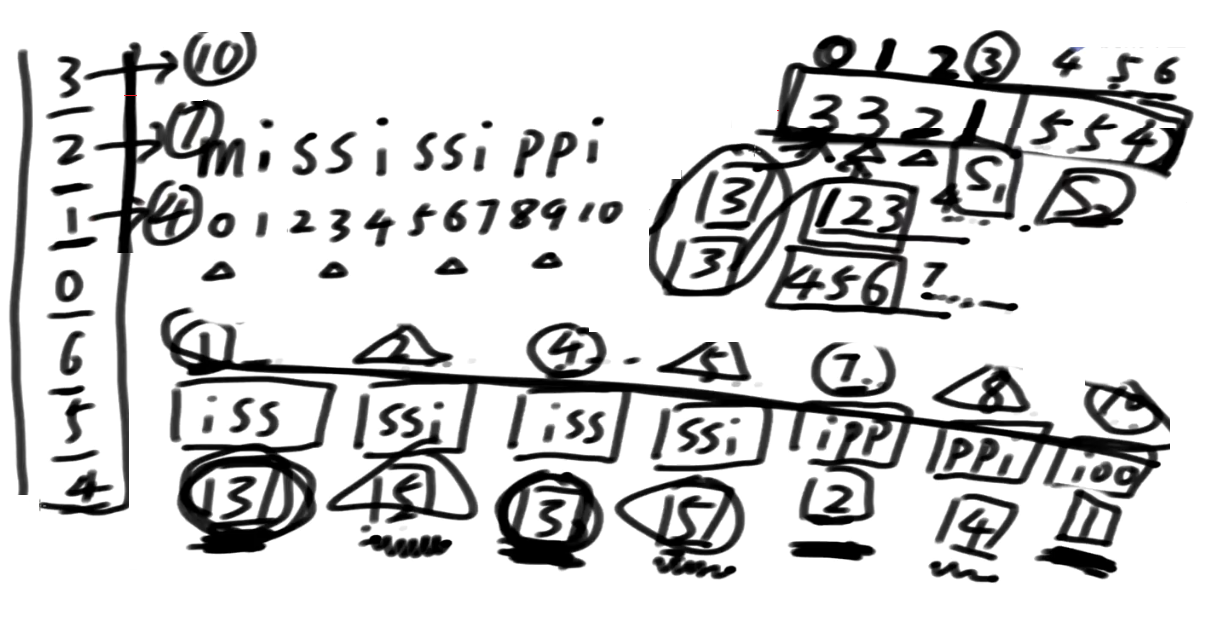
5: 234 5开头及其后面的所有
5: 567 8开头及其后面的所有
这个例子展示的是, 相同的排名信息落在一组里的情况, 都落在左组或者都落在右组
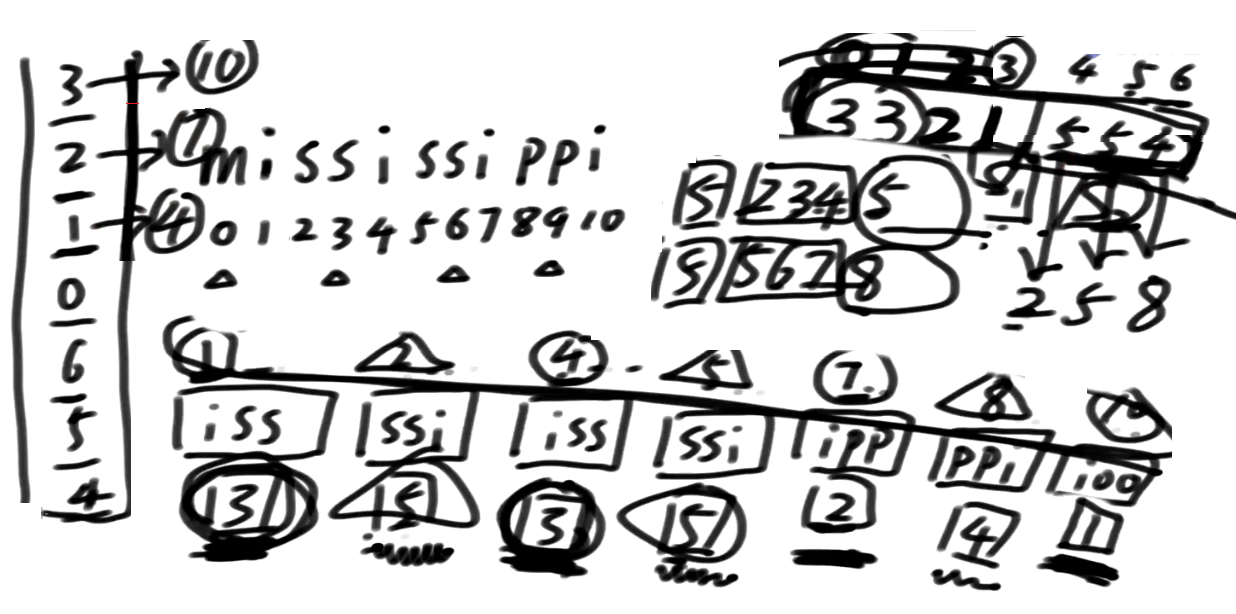
那如果相同的信息落在不同组呢?
其实相同的排名即便是跨组, 这么摆, 也能搞出区分来
比如说原始位置为1和5的两个位置,它们在非严格区分排名中都是第3名
看看下一位的信息:
123,下一位为4,在新数组中紧靠着1,假设排名为x
567,下一位为8,在新数组中紧靠着5,假设排名为y
那么现在需要比较 3_x 以及 3_y的大小,这个显然与新数组的后缀树的排名仍然是保持一致的。
那么也就是说无论相同信息落在同一组还是不同组,都能验证上面的结论。
S1及S2交接位置处理
现在还有一个小坑:S1类以及S2类交接的位置相同时如何比较排名
这里如果S1的最后一位本来就补了0,那么S2中的数顺着S1往后一定可以找到不同的3位后缀
如果S1的最后一位实在无法补0,那我们人为给S1补一个000
- 假设长度 % 3 == 2
S1的最后一位会补0,因此S2中的后缀值一定能够与它分出胜负
比如说长度为11,索引为 0~10,10的3位后缀,后面有两位用0补了
那么索引为2的后缀 与1、4、7 相等时,1、4、7对应的后缀为 4、7、10及后面的数字,这个其实在SA12中都有了,而且值也是正常的,唯一有点差异的是 索引为 10的,假设 num[2] = num[10] = 5,那么2的三个数的后缀位 5xy,x>0,y>0,而10的三个数的后缀位为500,基数排序时已经分出胜负了
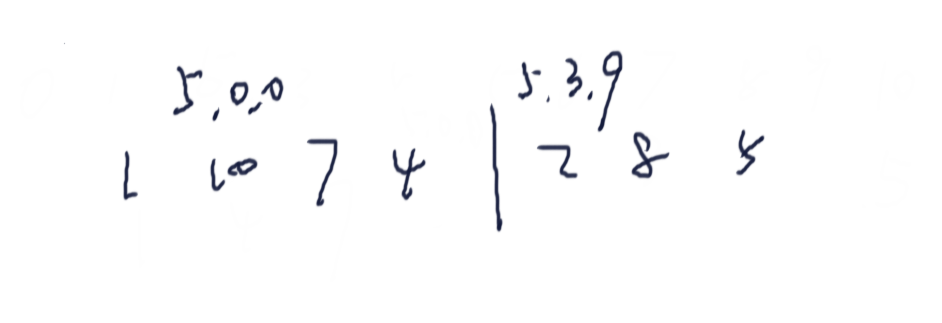
- 假设长度 % 3 == 0
情况与 长度 % 3 == 2 类似,此时 S1的最后一位会补0,S2中顺着S1至少可以找到一个不同值。
比如长度为9,索引为 0~8,S2前面的值与S1比较逻辑与上面的类似,如果是索引为8和索引为7的3位后缀进行比较,假设在这两个索引上的数字都是5,那么7对应550,8对应500,基数排序后 7 本来就在8的后面。
- 假设长度 % 3 == 1
S1的最后一个值它没有填充0,那么就会导致S2中的3位后缀可能与S1中的三位后缀没法进行比较
考虑下面这种极端情况,S2中的2号索引后缀为222,它与S1中任意一个数都无法严格比较出来大小
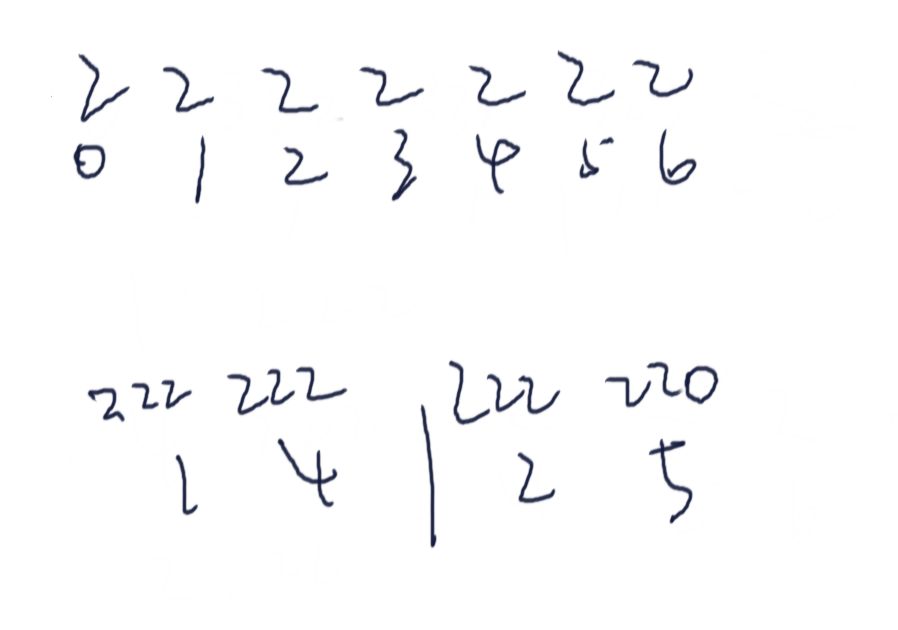
此时给S1补一个000就可以解决这个问题
此时2号索引就比7号索引的数要大了

当SA12整体排完序与 SA0 merge的时候,不考虑这个000就可以了
其实这个也很好实现,由于补的这个000在SA中一定有且仅有1个,且一定排在第0位(它最小)
我们直接从第1位开始与 SA0 比较就可以啦
时间复杂度
step2以及step3的时间复杂度都是O(N)
重点分析 step1 的时间复杂度:
-
如果3维信息没有办法确定精确排名, 我们需要进一个递归
-
这个递归是把s12类所有下标所对应的排名值作为一个新的字符串数组传进去的,
-
毫无疑问它的代价是T(2N/3), 因为只包含S12类, S0类被扣掉了
-
所以最差情况下:T(N) = T(2N/3) + O(N)
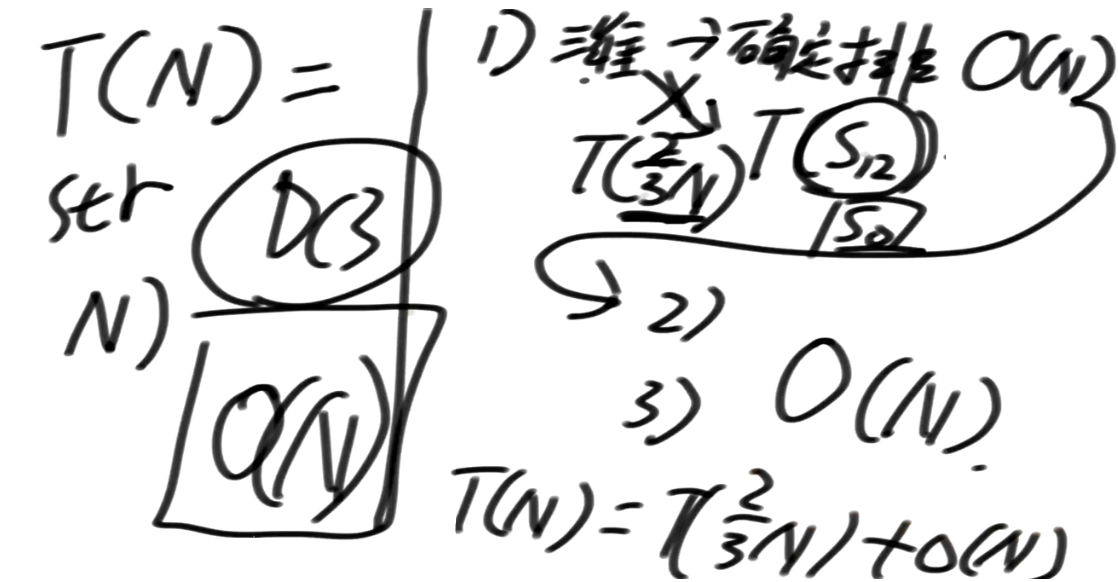
我们来回顾一下Master公式
形如 **T(N) = a * T(N/b) + O(N^d)**(其中的a、b、d都是常数)的递归函数,可以直接通过Master公式来确定时间复杂度
-
如果 log(b,a) < d,复杂度为O(N^d)
-
如果 log(b,a) > d,复杂度为O(N^log(b,a))
-
如果 log(b,a) == d,复杂度为O(N^d * logN)
对于step1:T(N)=T(2N/3)+O(N)==>a=1,b=3/2,d=1
于是 log(3/2, 1) = 0 < 1 = d
因此step1时间复杂度为 O(N^d) = O(N)
所以整体时间复杂度也为 O(N)
衍生数组
做题过程中,有时候只有 sa 数组还无法求解,可能还需要 rank 数组和 height 数组
但是这两个数组都可以通过 sa 数组在 O(N) 的时间复杂度下转换过来
rank数组
回顾一下两个概念
-
sa[i]:排名为i的后缀数组的开始索引
-
rank[i]:以 i 为开头索引的后缀数组的排名
由sa定义可知: sa[i] 为开始索引的后缀数组的排名必然是i
带入到 rank定义,必然有:rank[sa[i]] = i
前面已经求得了 sa数组:
遍历一遍sa数组,填入 rank 数组的值:rank[sa[i]] = i,即可获得rank数组,时间复杂度O(N)
height数组
height数组表示sa数组中相邻后缀的最长公共前缀长度表示sa数组中相邻后缀的最长公共前缀长度
以 banana 为例:
由之前的推导容易知道,sa中对应的字符串排序为 a, ana, anana, banana, na, nana
计算最长公共前缀(Longest Common Prefix,LCP):
| 相邻后缀对 | LCP |
|---|---|
| $ 和 a$ | 0 |
| a$ 和 ana$ | 1 |
| ana$ 和 anana$ | 3 |
| anana$ 和 banana$ | 0 |
| banana$ 和 na$ | 0 |
| na$ 和 nana$ | 2 |
所以,height数组为:0,1,3,0,0,2
可以看到,如果我们硬算,这个时间复杂度为 O(N^2),我们需要想办法将这个时间辅助度减到O(N)
我们构造一个 h 数组:
h[i] 表示的是:假设以 i 开头的后缀数组在后缀数组中排名为第 x,我们计算第 x - 1 名的后缀与以i开头的后缀数组的最长公共前缀,即为 h[i]。
上面的 以 i 开头的后缀数组在后缀数组中排名其实也就是 rank[i]
第 x - 1 名开头的后缀也就是以 sa[rank[i]-1] 开头的
还是以 banana 为例,由前述我们已经计算出 sa 数组以及 rank 数组:
-
sa: [5, 3, 1, 0, 4, 2]
-
rank: [3, 2, 5, 1, 4, 0]
| i | 对应后缀 | rank[i] | rank[i]-1 | sa[rank[i]-1] | 前一排名后缀 | LCP |
|---|---|---|---|---|---|---|
| 0 | banana$ | 3 | 2 | 1 | anana$ | 0 |
| 1 | anana$ | 2 | 1 | 3 | ana$ | 3 |
| 2 | nana$ | 5 | 4 | 4 | na$ | 2 |
| 3 | ana$ | 1 | 0 | 5 | a$ | 1 |
| 4 | na$ | 4 | 3 | 0 | banana$ | 0 |
| 5 | a$ | 0 | - | - | $ | 0 |
那么我们就可以求得 h[i] 的值为 [0,3,2,1,0,0]
而 height[rank[i]] = h[i],所以可以求出 height[i] 的值为 [0, 1, 3, 0, 0, 2]
由上面的分析,如果能得到 h[i],由于 sa[i] 和 rank[i] 已经求得
遍历h[i],转换为height[i] 即可,时间复杂度也是 O(N)
现在的重点是将求解 h[i] 的过程压缩到O(N)
先给出结论:h[i+1] >= h[i] - 1(后面会证明)
于是我们可以定义一个变量k记录 h[i] 的值,k取值为0~N
那么我们计算h[i+1] 时,可以知道 rank[i+1] 以及 rank[i+1] - 1 位置的字符串至少有k-1个前缀是相同的
因此遍历过程中的每一步k最多只能后退一步,整个过程下来,k最多回退N步。
于是,我们找到了一个变量,它最多走了2N步,而k每走一步计算的值都是常数项,没有迭代过程,因此整个计算过程的时间复杂度也是O(N)
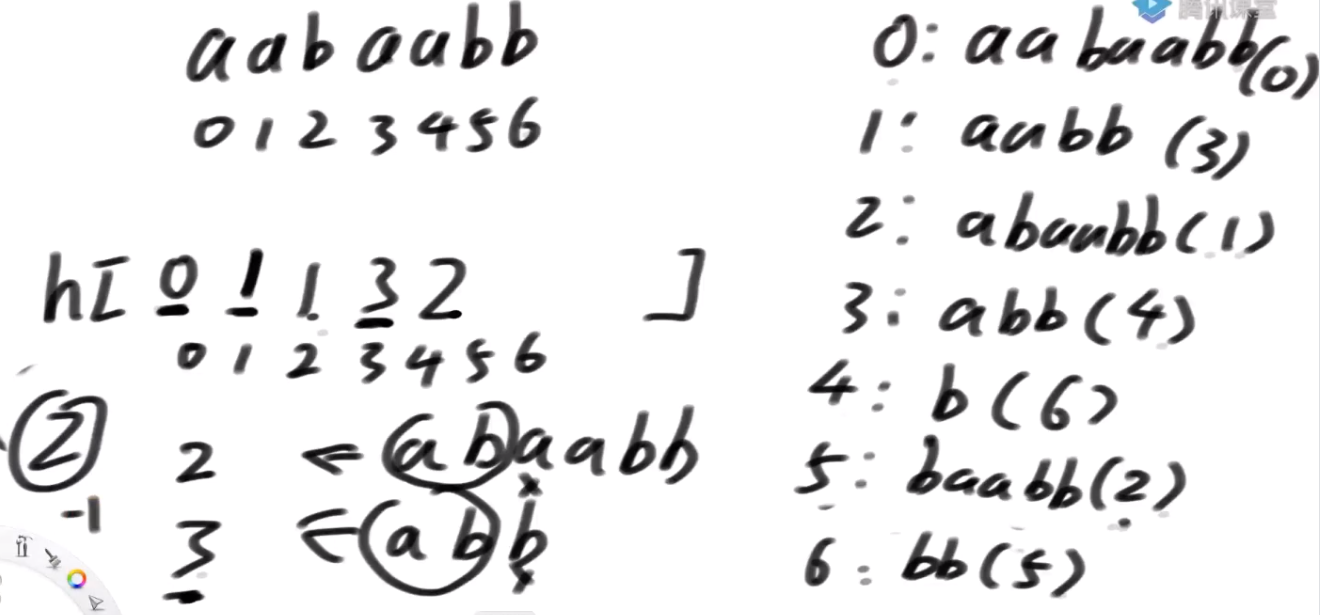
计算流程已经确定下来了,接下来我们来证明: h[i+1] >= h[i] - 1
- 对i位置
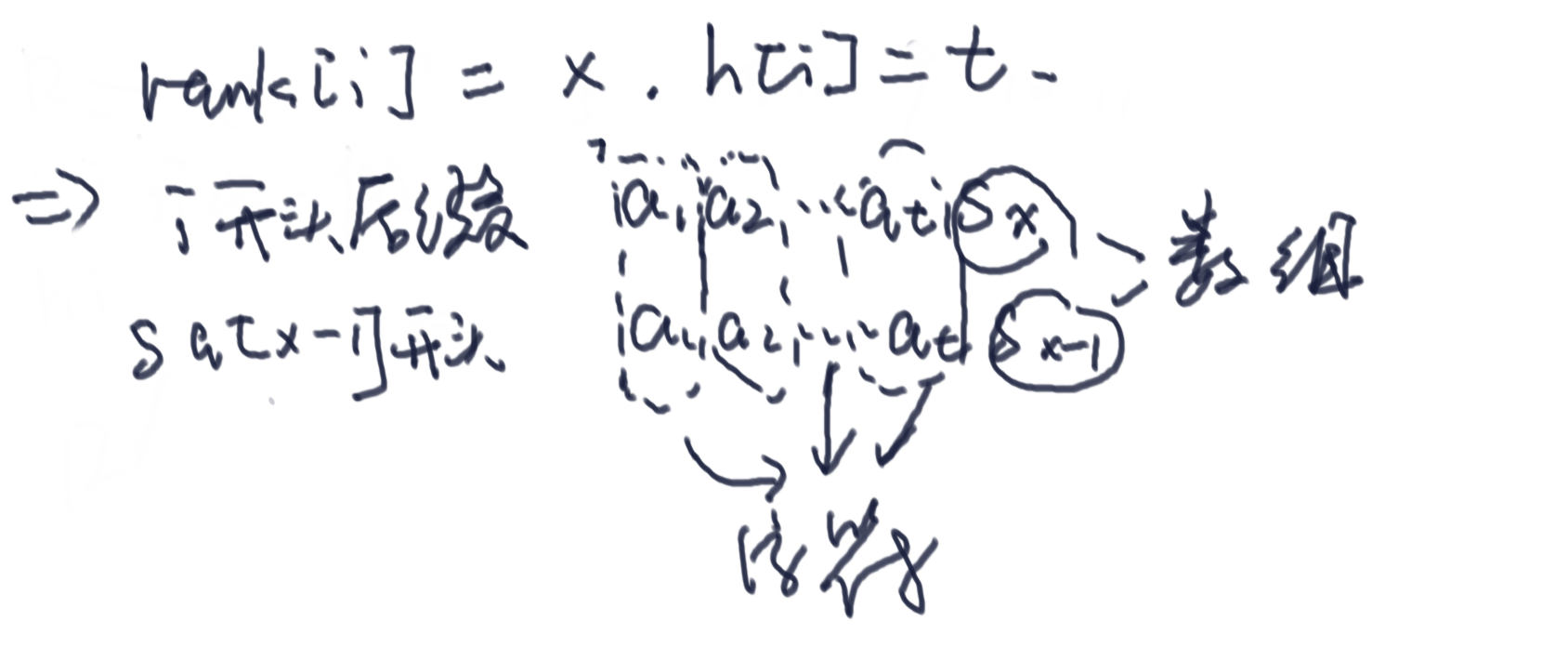
- 对 i+1位置
来到了i+1,我们设_rank[i+1] = y_,由于 i+1 正好在 i 后面一位
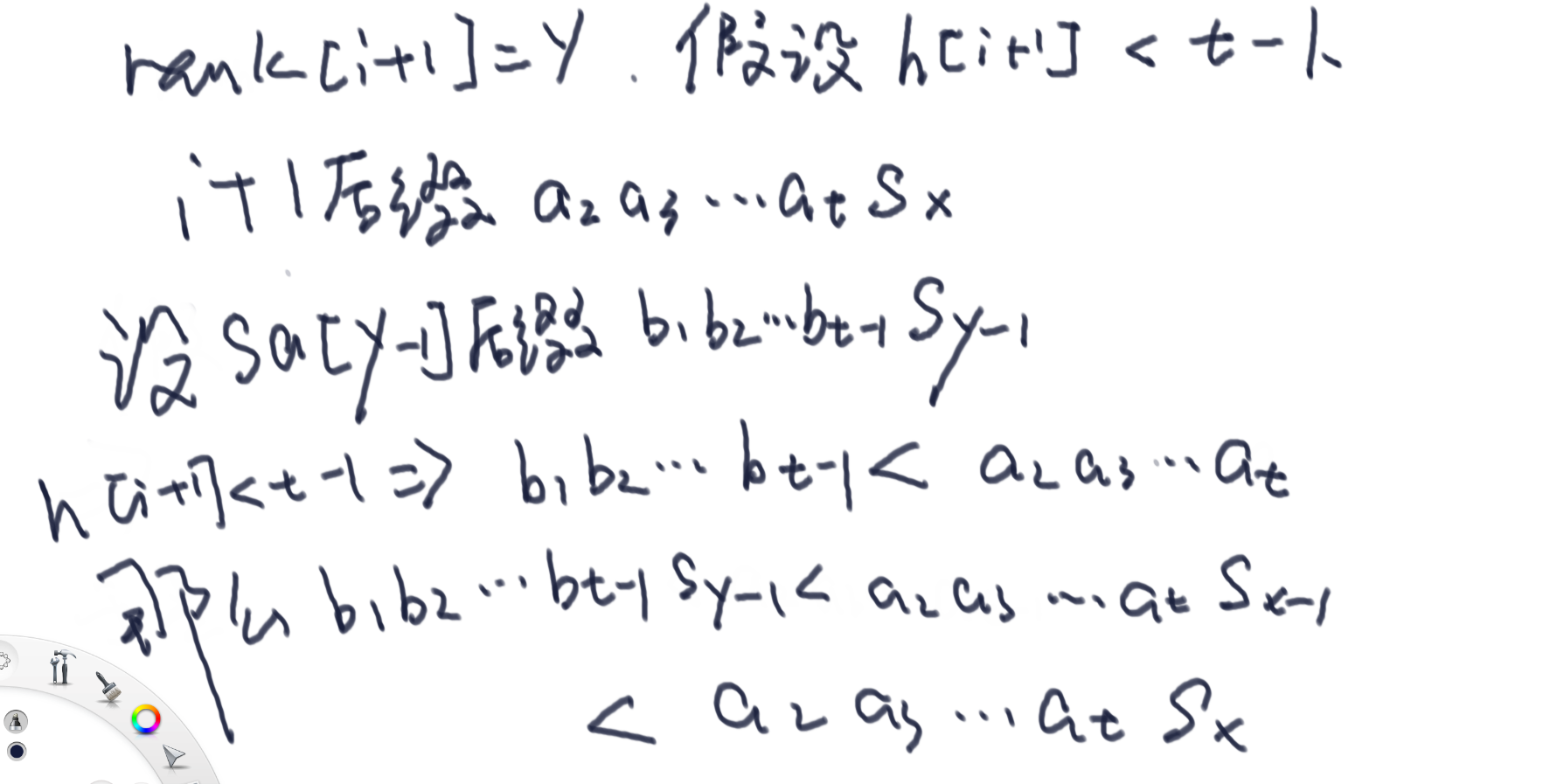

于是,我们得到 h[i+1] < h[i] - 1 是不成立的,必然有 h[i+1] >= h[i] - 1
于是:height 数组可以通过 sa 数组以及 rank 数组在 O(N) 内获得
整体梳理
0类是跳过的
s1类是画方块的, 1, 4, 7, 10 所属的排名组成一个数组, 3, 3, 2, 1
s2类 没画方块的, 2, 5, 8 所属的排名组成一个数组, 5, 5, 4
这个数组[3 3 2 1 5 5 4] 把每个位置的排名认为是一个字符, 哪怕它20 也认为是一个字符 不把它拆开, 哪怕是2000也一样
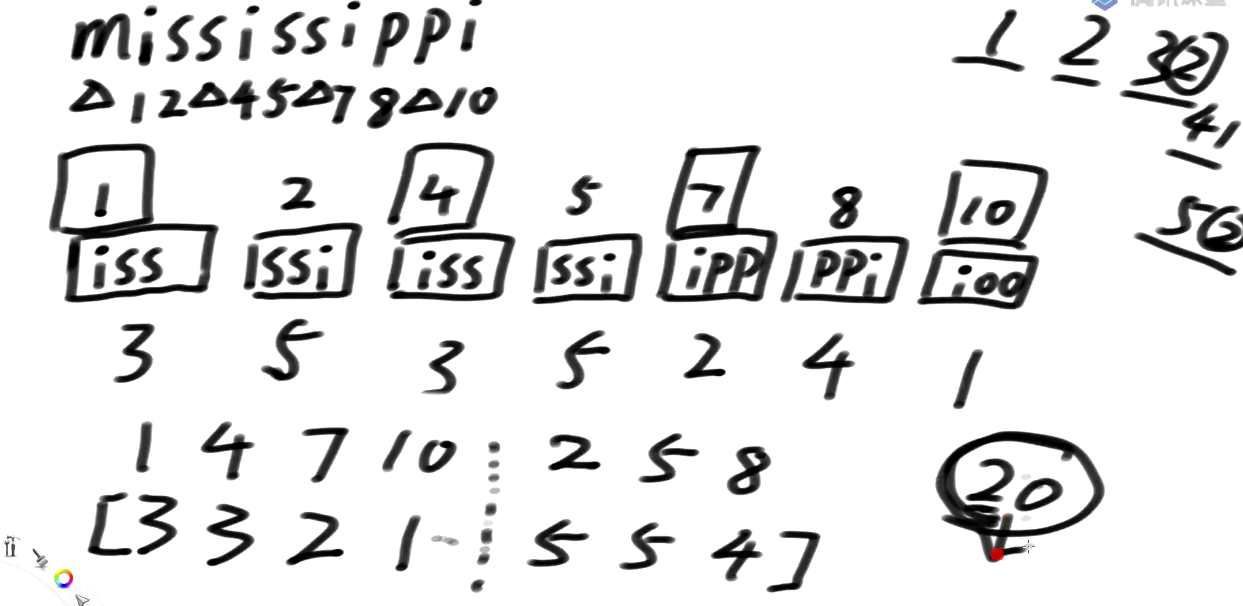
接下来把 3321554理解为一个字符串, 去求它的后缀数组排名
新的数组中:下标3是第一名, 对应回原数组是10下标, 就认为 原来的这些 1,2,4,5,7,8,10之间, 10排第一个,7排第二个,也就是你把这个数组求出来的后缀数组你对应回去, 就是原数组s12类的精确排名块之间不管怎么摆已经决出的排名会把这个顺序带下去
这么摆的原因是想区分一个块内部的排名, 如果已经区分出的排名, 我不管怎么摆它都不会乱
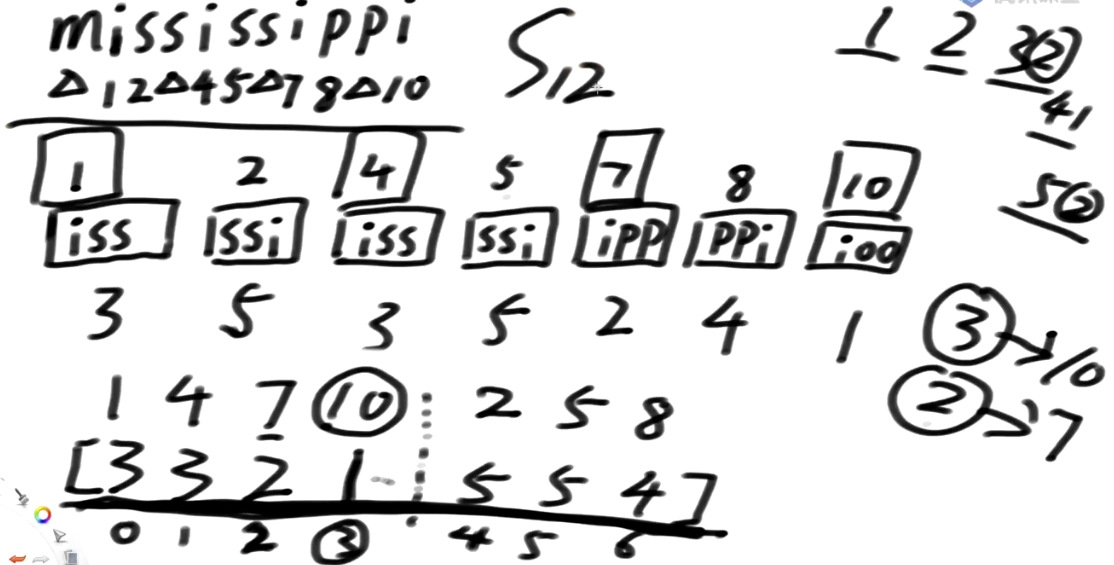
1开头的iss 123
4卡头的iss 456
这三个字符都相等, 所以需要
-
1开头的iss 123 4开头及其后面的所有的整体排名
-
4卡头的iss 456 7开头及其后面的所有的整体排名
摆放顺序正好能帮助我在同一块内部的排名决定
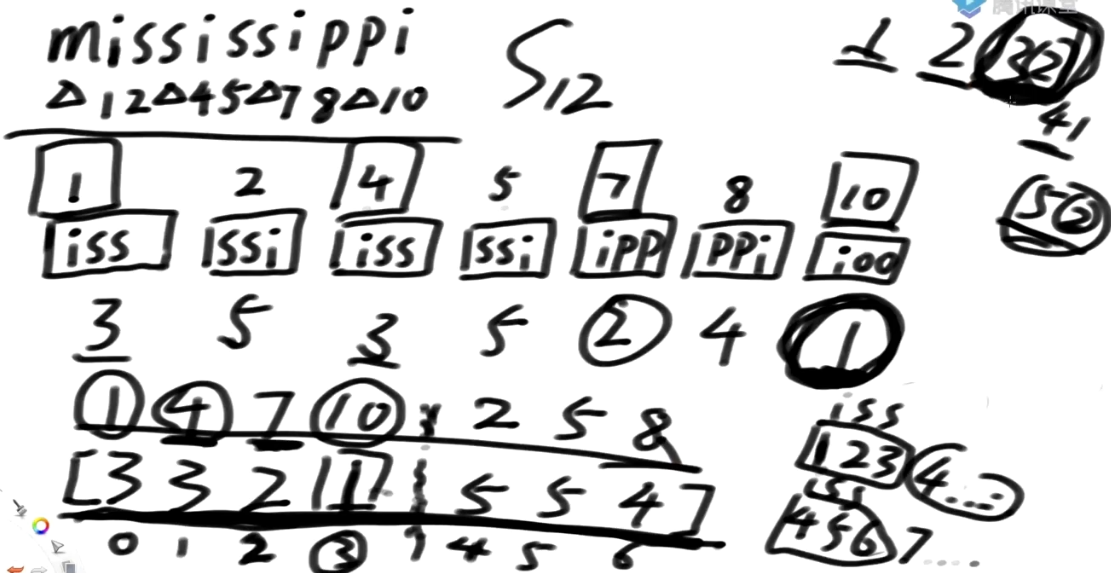
再串一遍
DC3算法:根据下标模3的算法
导入&铺垫
- N个样本数量很大(1000万个), 每个样本3纬数组, 里面数值不大,怎么排序能最快?
根据一, 二, 三维数据排序–>基数排序
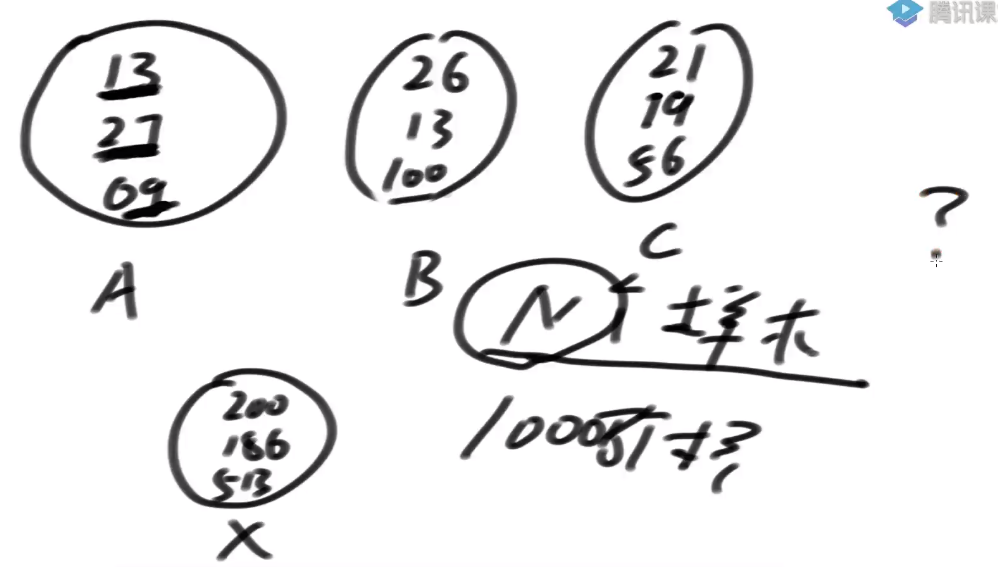
-
N个样本, 数据的维度不超过3维, 而且每一个维度值相对较小(比如1000以内), 排序的代价可以认为是O(N),一共进出桶3次
-
数组也可以计算后缀数组
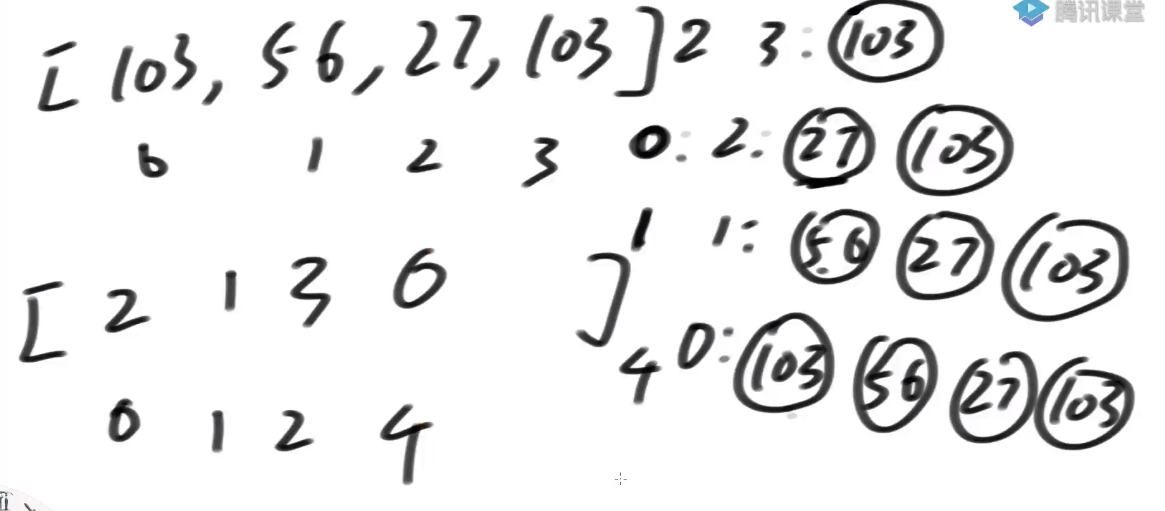
案例
- 假设一个字符串, 把它的下标按照模3分类
0%3 == 0, 0 类,
1%3 == 1, 1 类,
2%3 == 2, 2 类,
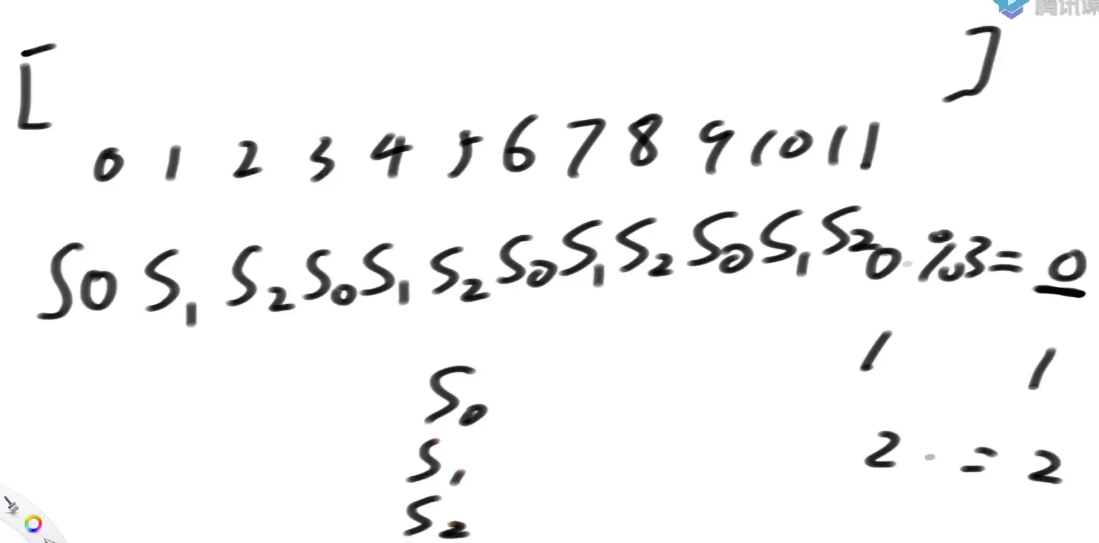
- S12类有哪些?
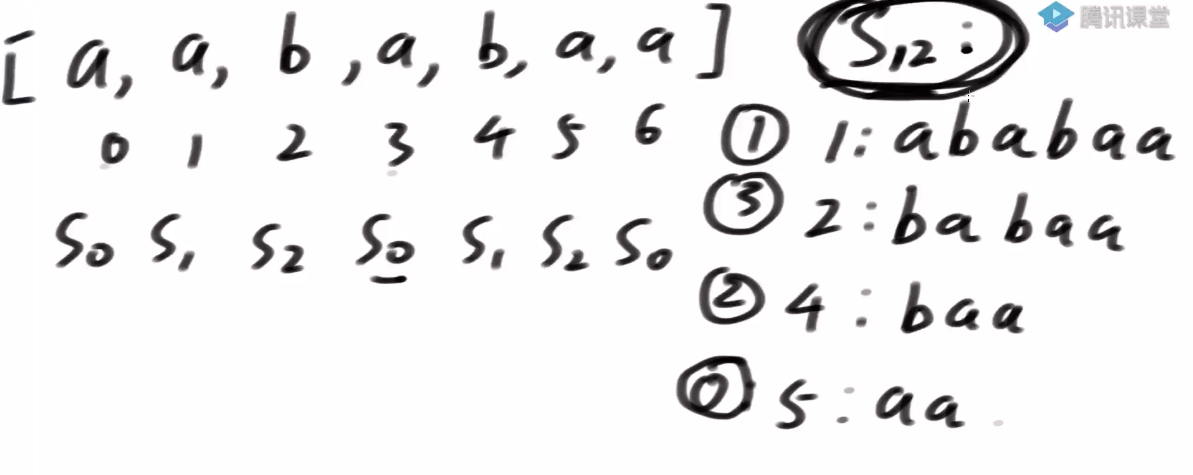
-
如果能得到S12类的排名, 能不能得到所有后缀串的排名?–>可以!
-
S0类的后缀串排名能不能得到呢? -->基数排序
所以当我有了 s12 名的排名之后, s0 内部的排名过一个基数排序可以直接决定
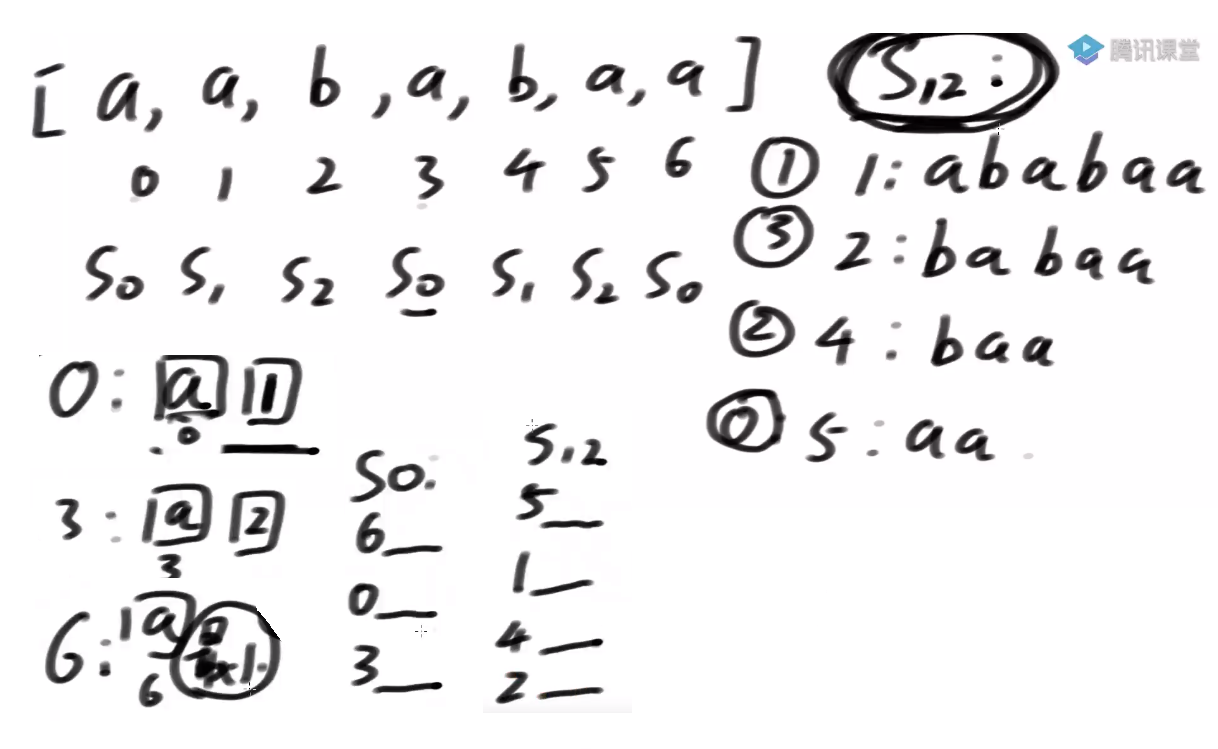
- 怎么得到总排名?
找一个merge, 怎么做?
先比较6开头的跟5开头的字符串
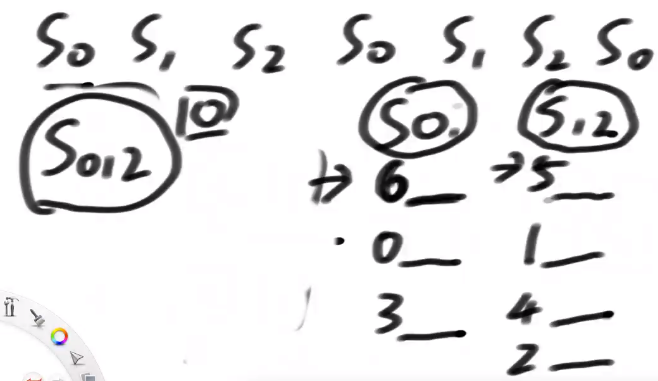
- S0类跟S2类最多比3回

- S0类跟S1类最多比两次

- 现在得到一个什么结论,如果我们有S12类排名的话,我们可以用O(N)的时间,导出S0内部排名
我们还用O(N)的时间merge s0s12整体出来的s012,后面的时间都是过基数排序,最多三类数据,
所以S12类排名这个事一旦搞定这个算法就是O(N)的
关键你怎么得到s12的排名?

怎么得到S12类的排名?
- 只拿前三个字符能得出精确排名?
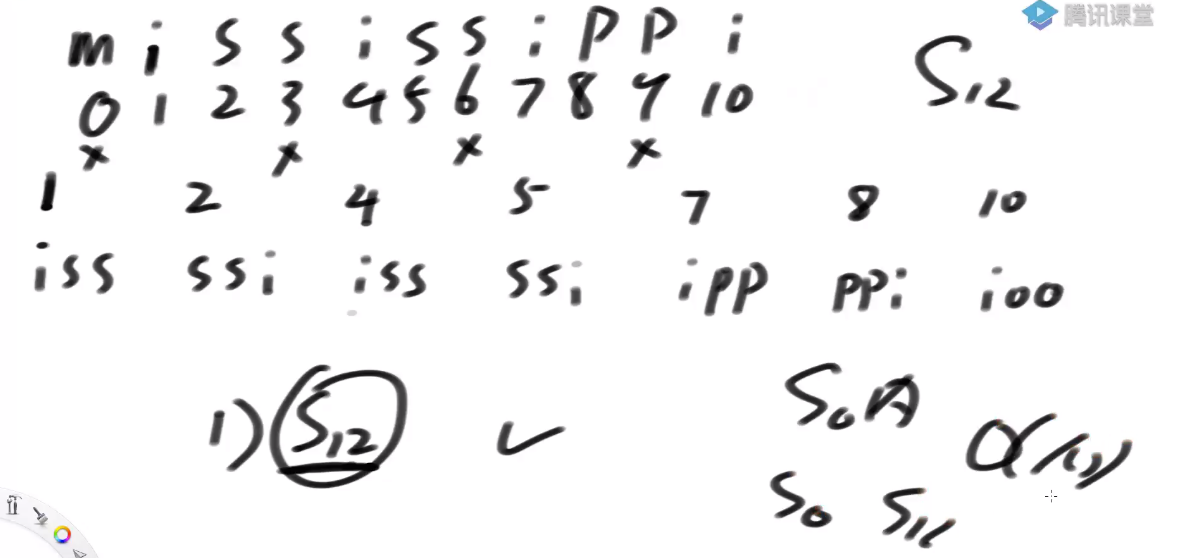
- 只拿前三位分不出精确排名

- 组成新数组, s1类放左边, s2类放右边

- 递归调用, 求数组的后缀数组排名 能够指导老数组的排名
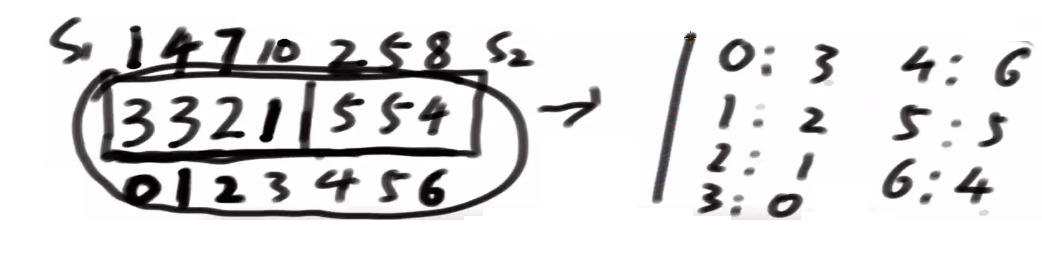

-
为什么s1左侧, s2右侧–>解决相同的排名问题
- 能不能通过这种构造导出严格排名,我缺的我就让他挨着我

-
s1跟s2不在一侧怎么确定排名?
- 相同排名不管是来自于S1内部的,还是来自于S2内部的,还是跨开的,这么放都能解决

- 边界补零处理

-
复杂度
-
如果s12类直接能用3维数据基数排序能搞定, 就不牵扯下面了
-
如果搞不定, 生成一个新数组, 长度为之前的2/3,只取1,2类出来放到新数组, 而每个数组中的值最大N, 因为排名最大值只能是 N, 对这数组再次基数排序
-
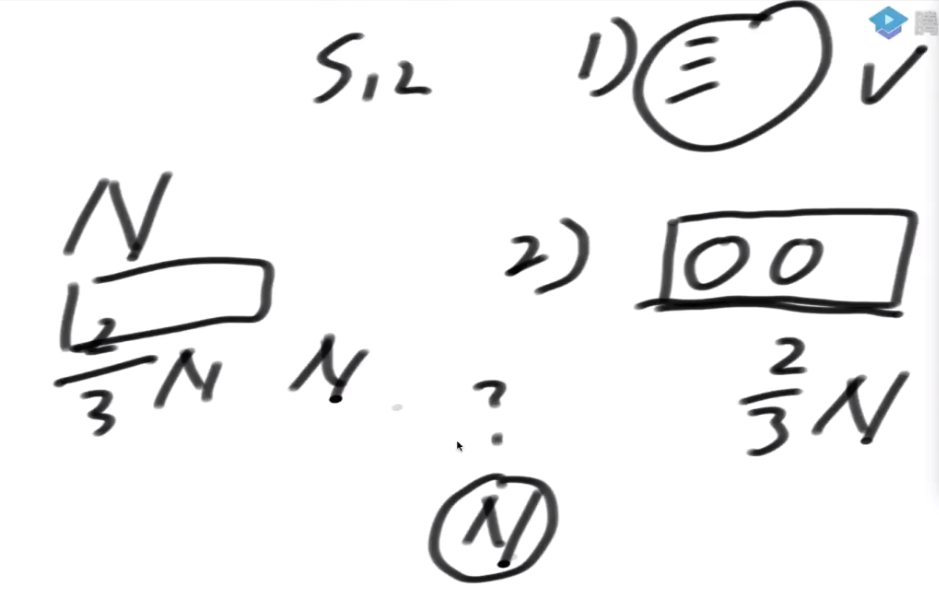
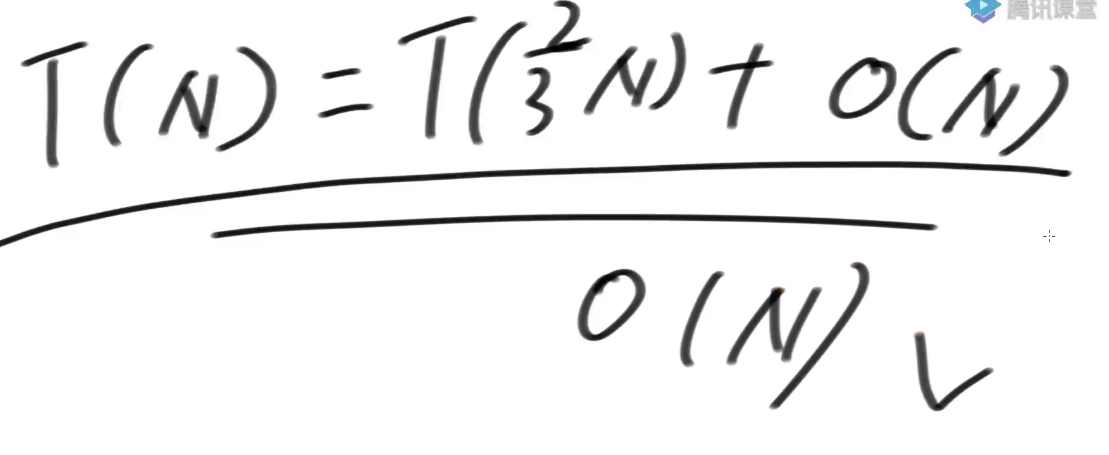
衍生数组
rank数组
遍历sa:rank[sa[i]] = i,计算rank数组
height数组
先计算 h 数组
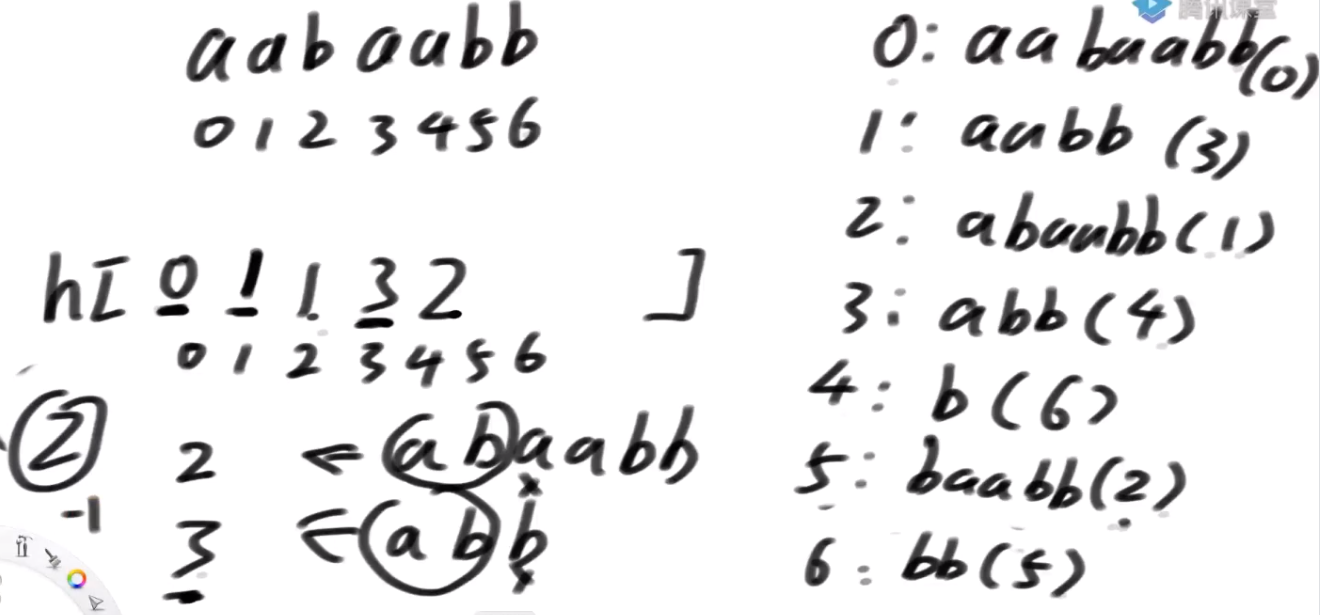
再将 h 转为 height
DC3代码实现
原论文中,有C++代码的实现,这里主要讲一下 Java 版本的实现
public class DC3 {
/**
* suffix array
* <p>sa[i]: 后缀数组中排名为i的索引
*/
public int[] sa;
/**
* rank[i]: 索引为i的后缀数组的排名
*/
public int[] rank;
/**
* 表示sa数组中相邻后缀的最长公共前缀长度
* <p>以banana为例, sa对应的字符串为 ['a', 'ana', 'anana', 'banana', 'na', 'nana']
* <p>sa中相邻后缀的最长公共前缀长度为:
* <p>$ 和 a$ 0
* <p>a$ 和 ana$ 1
* <p>ana$ 和 anana$ 3
* <p>anana$ 和 banana$ 0
* <p>banana$ 和 na$ 0
* <p>na$ 和 nana$ 2
* <p>height数组为 0,1,3,0,0,2
*/
public int[] height;
/**
* 构造方法的约定:
* 数组叫nums,如果你是字符串,请转成整型数组nums
* 数组中,最小值>=1
* 如果不满足,处理成满足的,也不会影响使用
* max, nums里面最大值是多少
*/
public DC3(int[] nums, int max) {
sa = sa(nums, max);
rank();
height(nums);
}
private int[] sa(int[] nums, int max) {
int n = nums.length;
int[] arr = new int[n + 3];
System.arraycopy(nums, 0, arr, 0, n);
return skew(arr, n, max);
}
/**
* sa的构造
* <p>案例说明:将 mississippi 按字符顺序转为 2, 1, 4, 4, 1, 4, 4, 1, 3, 3, 1
* <p>此时 nums = [2, 1, 4, 4, 1, 4, 4, 1, 3, 3, 1, 0, 0, 0],n=11,k=4
* <p>nums 后面加三个0,保证后面流程中取 3 个值后缀时不越界,同时 用 0 填充不会破会排序
* <p>====================================================================
* <p>这里埋个坑:如果只是三位后缀那么 nums 长度 +2 就够用了,为啥还要 +3 呢?后面解释
* <p>====================================================================
* <p>********************************************************************
* <p>这个案例,没有考虑 S1 补 0 的操作
* <p>有兴趣的话可以拿 nums=[2,2,2,2,2,2,2] 做尝试
* <p>********************************************************************
*
* @param nums 在原有数组基础上, 末尾添加了三个0
* @param n 原有数组的长度
* @param K 数组中的最大值
* @return 构造好的sa数组
*/
private int[] skew(int[] nums, int n, int K) {
int n0 = (n + 2) / 3, n1 = (n + 1) / 3, n2 = n / 3, n02 = n0 + n2;
// SA12 用来记录 S1 以及 S2 分组下的 sa 值
// s12 是一个辅助数组用来帮助计算 SA12
int[] s12 = new int[n02 + 3], SA12 = new int[n02 + 3];
// 初始化 s12,作为第一次基数排序的输入索引
// ====================================================================
// 这里为啥是 n + (n0 - n1) 呢,
// =====>>>>> 因为我们有可能对 S1 做补0 操作 important!!!!!!!!!! <<<<<=====
// 当 n % 3 == 1 时,n0 - n1 == 1,我们需要对 S1 做补0操作
// 这就是 S1 与 S2 比较时的边界处理
// 如果真的需要补0,比如说 n == 7,nums的 index 需要取到9,此时 nums 长度为10
// 这也就是为什么 nums 一开始需要补 3 个 0,而不是补 2 个 0 的原因
// ====================================================================
for (int i = 0, j = 0; i < n + (n0 - n1); ++i) {
if (0 != i % 3) {
s12[j++] = i;
}
}
// 下面三个步骤其实就是在对 s12 中的相邻三个数字进行基数排序
// 由于 s12 中已经有初始化的索引值
// 第1轮:s12作为输入索引值,对3位(0~2)中的第2位进行排序,排序后索引写入 SA12 中
// 第2轮:SA12作为输入索引值,对3位(0~2)中的第1位进行排序,排序后索引写入 s12 中
// 第3轮:s12作为输入索引值,对3位(0~2)中的第0位(当前位)进行排序,排序后索引写入 SA12 中
// 经过三轮排序以后:SA12中记录的就是S12分组中所有数字取3位后缀的从小到大的排序
// 当然,这个排序不一定是严格的,如果所有3位后缀排序都不相等,S12的排序就结束了
// 如果有相等的,进行下一轮排序
// ==================================== e.g. ====================================
// 假设原始数组
// 索引 0 1 2 3 4 5 6 7 8 9 10
// 数字 2 1 4 4 1 4 4 1 3 3 1
// 那么s12位的数组分别为索引 1 2 4 5 7 8 10
// _________________数值 1,4,4 4,4,1 1,4,4 4,4,1 1,3,3 3,3,1 1,0,0
// ==================================== end. ====================================
// 对3位(0~2)中的第2位进行排序
radixPass(nums, s12, SA12, 2, n02, K);
// 对3位(0~2)中的第1位进行排序
// 这里比较的是 4 4 4 4 3 3 0(第一轮已经按照第2位排序了,这里顺序不一定正确了)
radixPass(nums, SA12, s12, 1, n02, K);
// 对3位(0~2)中的第0位进行排序
radixPass(nums, s12, SA12, 0, n02, K);
// 经过三轮之后 SA12 中已经记录了 S1 及 S2 分组所有的索引前三个数字的排序
// ===================================================================
// 但是由于值比较了三个数字,这种排序可能不是严格的增加,继续上面的例子
// SA12 -> 10 7 1 4 8 2 5
// 对应3个数字 1,0,0 1,3,3 1,4,4 1,4,4 3,3,1 4,4,1 4,4,1
// ===================================================================
// name: 记录 SA12 中三个数字后缀真实的排名,如果有重复,则记录重复的排名
// 这里的 name 就是要判断 s12 按照只取三个数字进行排序的结果中是否有重复的情况
// c0 c1 c2 分别记录在 SA12 索引、索引+1、索引+2 元素,当前的大小
int name = 0, c0 = -1, c1 = -1, c2 = -1;
for (int i = 0; i < n02; ++i) {
// 比较 SA12 前一个与当前索引下的 3个数字的后缀是否完全相同
// 如果不完全相同,说明 3个数字组成的后缀不同,此时 name 可以+1
// 第一次必定不会相等,name至少经历了一次 +1
if (c0 != nums[SA12[i]] || c1 != nums[SA12[i] + 1] || c2 != nums[SA12[i] + 2]) {
name++;
c0 = nums[SA12[i]];
c1 = nums[SA12[i] + 1];
c2 = nums[SA12[i] + 2];
}
// 无论 name 是否 +1,都将 SA12 中的索引按照 S1 以及 S2 区分好 放在 s12 中
// 由前述,走到这里 name 至少经历了一次 +1,所以 s12 中 value 值为 1~max(name)
// S1 放前面,S2 放后面
if (1 == SA12[i] % 3) { // 情况 S1
s12[SA12[i] / 3] = name;
} else { // 情况 S2,s12中索引 + n0,正好放在 S1 后面
s12[SA12[i] / 3 + n0] = name;
}
}
// 第一次走到这里(还没有进入 skew递归)
// s12 = [ 3, 3, 2, 1, 5, 5, 4, 0, 0, 0]
// SA12 = [10, 7, 1, 4, 8, 2, 5, 0, 0, 0]
if (name < n02) { // 只取前三个数字, s12 中有重复的排序
// 递归调用该方法进行重排序
// 调用前 s12 = [ 3, 3, 2, 1, 5, 5, 4, 0, 0, 0]
// .....sa12 = [10, 7, 1, 4, 8, 2, 5, 0, 0, 0]
// n02=7 name=5
SA12 = skew(s12, n02, name);
// 递归完成后 SA12 中是 S12 中的索引(不是原始索引!后面分析)
// 将 SA12 中排序填充到 s12 中
// 此时 s12 作用类似于 rank 数组(同样不是原始索引)
// ====================================================
// 调用后 s12 = [ 3, 3, 2, 1, 5, 5, 4, 0, 0, 0]
// .....sa12 = [ 3, 2, 1, 0, 6, 5, 4]
// ====================================================
// ****************************************************
// s12 在后面的作用只是用来判断相对大小,删除后跑对数器能过
// 也就是说这里其实是可以删掉的
// 只是留在这里语义更加明确,而且对总体时间复杂度也没有影响
// 原始论文里面附带的 C++ 代码也是有这个循环的
// ****************************************************
for (int i = 0; i < n02; i++) {
s12[SA12[i]] = i + 1;
}
// ====================================================
// 填充 s12
// 填充后 s12 = [ 4, 3, 1, 5, 7, 6, 2]
// .....sa12 = [ 3, 2, 1, 0, 6, 5, 4]
// ====================================================
// ****************************************************
// =====>>>>> 这里的 sa12 里面的索引到底是个啥?? <<<<<=====
// 我们可以这么理解
// 先把 S1 抽出来,从左到右排个序,记做 0 1 ... x
// 然后 S2 抽出来,从左往右拍个序,记做 x+1 x+2 ...
// 例如 假设原来有 11 个数,索引为 0~10
// 那么 S1 1 4 7 10,SA12 中值表示的索引为 0 1 2 3
// S2 2 5 8,SA12 中值表示的索引为 4 5 6
// 也即是:
// 原始索引...。 0 1 2 3 4 5 6 7 8 9 10
// S12值对应索引 0 4 1 5 2 6 3
// 抽象化一下:
// SA12[i] = j,那么 j < n0,那么对应原始索引为 j*3+1
// SA12[i] = j,那么 j >= n0,那么对应原始索引为 (j-n0)*3+2
// ****************************************************
// ####################################################
// 上面的案例是一个特例,S12中的S1正好都在左边,S2正好都在右边
// 其实 SA12 中着两个是可以混着来的,比如说
// SA12 = [2, 6, 1, 0, 3, 5, 4]
// s12 = [4, 3, 1, 5, 7, 6, 2]
// 假设原始数组长度还是 11,那么将 SA12 中的值还原到原始数组以后为
// .......[7, 8, 4, 1,10, 5, 2]
// ####################################################
} else { // 只取前三个数字, s12 中已经没有重复的排序了
// 直接将 s12中的值赋值给 SA12 即可
for (int i = 0; i < n02; i++) {
SA12[s12[i] - 1] = i;
}
}
// SA0 用于记录 S0 组内的排序, s0 辅助计算 SA0
int[] s0 = new int[n0], SA0 = new int[n0];
// 初始化第0组的索引,值存到 s0 中
// ========================================================
// 这里有个小技巧,S0后面接的都是S1
// 如果最后一组有 S0 没有S1,由前所述,会给S1补一个000作为最后一个S1
// ========================================================
for (int i = 0, j = 0; i < n02; i++) {
if (SA12[i] < n0) {
s0[j++] = 3 * SA12[i];
}
}
// 基数排序
// ========================================================
// 由前所述,s0初始化为 S1 的排序
// 这里并不是按照 0 3 6 9 的顺序,而是按照 S12 中 S1 的顺序来初始化
// 这里的基数排序是有稳定性的,值相同时不会破坏原有数组的相对顺序
// 因此这个基数排序会优先按照 S0 位置排序,S0相同时就按照添加顺序排序
// 而添加顺序就是 S0 后面紧跟的 S1 的排序
// 双重操作,保证 SA0 中 S0 分组所有值的位置绝对有序
// ========================================================
radixPass(nums, s0, SA0, 0, n0, K);
int[] sa = new int[n];
// 这一轮循环就是 SA0 于 SA12 的 merge 过程了
// p 记录 SA0 的位置,t 记录 SA12 的位置,一个典型的双指针合并有序数组问题
// ====================================================================
// 为什么 t 从 n0 - n1 开始?
// 当 n0 - n1 == 1时,之前对 S1 进行了补0操作,这里跳过这一个就可以了
// ====================================================================
for (int p = 0, t = n0 - n1, k = 0; k < n; k++) {
// 前面已经分析过,这里就是将 SA12 值中的索引还原为原始数组中的索引
int i = SA12[t] < n0 ? SA12[t] * 3 + 1 : (SA12[t] - n0) * 3 + 2;
int j = SA0[p];
if (SA12[t] < n0 ?
// SA12[t] < n0,表示是 S0 与 S1 比较, 最多比较2个数
leq(nums[i], s12[SA12[t] + n0], nums[j], s12[j / 3])
// SA12[t] >= n0,表示 S0 与 S2 比较, 最多比较3个数
: leq(nums[i], nums[i + 1], s12[SA12[t] - n0 + 1], nums[j], nums[j + 1], s12[j / 3 + n0])
) {
// 这个分支是 SA12 < SA0 的情况
// 注意:最多三个值绝对可以区分出来,这里不可能取到 == 号
sa[k] = i;
t++;
// SA12 分支走完了,用剩下的 SA0 值填充答案
if (t == n02) {
for (k++; p < n0; p++, k++) {
sa[k] = SA0[p];
}
}
} else {
// 这个分支是 SA12 > SA0 的情况
sa[k] = j;
p++;
// S0 分支走完了,用剩下的 SA12 值填充答案
if (p == n0) {
for (k++; t < n02; t++, k++) {
sa[k] = SA12[t] < n0 ? SA12[t] * 3 + 1 : (SA12[t] - n0) * 3 + 2;
}
}
}
}
return sa;
}
/**
* 扩展的基数排序
* <p>e.g. nums = [2,9,7,3,5,6,1,3,10] input=[1,3,5] offset=2 n=3 k=9
* <p>.............0 1 2 3 4 5 6 7 8
* <p>那么我们需要对 input[i] + offset 位置的数字 进行排序
* <p>也即是对 3 5 7 位数字排序,对应的数值也就是 3 6 3
* <p>排完序以后就是 3 3 6,对应的原始索引为 1 5 3,再将结果写到 output中
* <p>因此,最终 output 为 [1,5,3]
*
* @param nums 原始数组
* @param input 待排序值对应数组的开始位置
* @param output 排序后结果存放的位置
* @param offset 待排序值对应数组的开始位置距离的偏移量
* @param n 待排序的数据量大小
* @param k 原始数组的最大值, 决定了桶的大小
*/
private void radixPass(int[] nums, int[] input, int[] output, int offset, int n, int k) {
int[] cnt = new int[k + 1];
// 这一轮循环结束后 cnt[x] 表示的是 nums[input[i] + offset] == x 的个数
for (int i = 0; i < n; ++i) {
cnt[nums[input[i] + offset]]++;
}
// 对 cnt 的前 i-1 位进行累加
// 例如 0 0 0 2 0 0 1 0 0 0
// ==> 0 0 0 0 2 2 2 3 3 3
// 此时 cnt[x] 表示的是所有的数字中 小于 x 的个数
for (int i = 0, sum = 0; i < cnt.length; ++i) {
int t = cnt[i];
cnt[i] = sum;
sum += t;
}
// cnt[nums[input[i] + offset]] 获取的是 当前 == nums[input[i] + offset] 时的索引
// 获取以后 cnt[nums[input[i] + offset]]++, 那么下一次获取时就是当前索引 +1
for (int i = 0; i < n; ++i) {
output[cnt[nums[input[i] + offset]]++] = input[i];
}
}
/**
* 字典序 (a1,a2) <= (b1,b2)
*/
private boolean leq(int a1, int a2, int b1, int b2) {
return a1 < b1 || (a1 == b1 && a2 <= b2);
}
/**
* 字典序 (a1,a2,a3) <= (b1,b2,b3)
*/
private boolean leq(int a1, int a2, int a3, int b1, int b2, int b3) {
return a1 < b1 || (a1 == b1 && leq(a2, a3, b2, b3));
}
/**
* sa数组转rank数组: rank[sa[i]] = i
*/
private void rank() {
int n = sa.length;
rank = new int[n];
for (int i = 0; i < n; i++) {
rank[sa[i]] = i;
}
}
/**
* sa数组转height数组
* <p>转换为求h[i]:以 i 开头的后缀数组在后缀数组中排名为第 x
* <p>计算第 x - 1 名的后缀与以i开头的后缀数组的最长公共前缀
* <p>h[i+1] >= h[i] - 1,利用有限回退 => sa 以及 rank 转 h 数组复杂度 O(N)
*/
private void height(int[] s) {
int n = s.length;
height = new int[n];
// k 记录 h[i]
// 由于 h[i+1] 的最小值只由 h[i] - 1决定
// 没有必要再搞一个数组来专门存 h[i] (压缩的思想)
int k = 0;
for (int i = 0; i < n; ++i) {
// rank[i] == 0时,前面没有字符了,LCP必然为0,h[i] = height[i] = 0
if (rank[i] != 0) {
// k 最多回退一步
if (k > 0) {
--k;
}
int j = sa[rank[i] - 1];
// 只用比较 i 以及 sa[rank[i] - 1] >= k 位置的字符是否相同
// 相同则 k++,同时记录 height 结果
while (i + k < n && j + k < n && s[i + k] == s[j + k]) {
++k;
}
// h哥不在江湖,但 江湖仍然有h哥 的传说
// ==> h[i] = k
height[rank[i]] = k;
}
}
}
}
-
核心数组
-
sa数组:Suffix Array,sa[i]表示后缀数组按照从小到大,排在第i位的后缀树对应的原始数组中首个元素的排序
-
rank数组:rank[i]表示以i开头的后缀数组在所有后缀树组中的排名
-
height数组:表示sa数组中相邻后缀的最长公共前缀长度表示sa数组中相邻后缀的最长公共前缀长度
-
-
数组中最小值要求>=1
无非就是把原数组处理成每个值都是 大于等于 1 的
因为它内部有补0这件事, 所以原数组不能出现1以下的
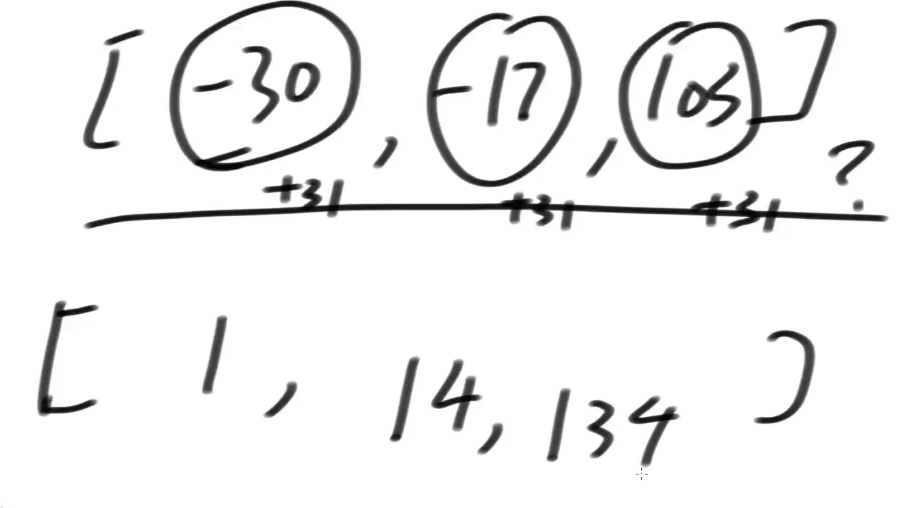

- 高度数组怎么生成?
生成后缀数组之后RMQ就生成了
高度数组: 就是拿后缀数组跟rank数组生成, 得到高度数组, RMQ数组就是由高度组成的
-
里面一个没被注意的细节
-
后缀数组中, 这个字符串每个ASCII码不要太大, 但是你后面把排名值变成了字符串类型的数组.会不会导致你这里面的值过大呢?不会
- 如果我长度为N, 我把排名值作为值的话, 每个值的大小不会超过长度N
-
如果在一个数组中, 长度N, 每个位置的值, 不超过N, 如果我想做基数排序
-
还是O(N)的问题
-
准备N个桶, 所有对象进去再倒出来, 还是O(N)
-
后序的过程, 有可能导致长度比较大, 但是即便如此, 依然O(N)
-
-
- 给出的模板怎么使用?

-
后缀数组 的 数组的方式使用
- 用模板时需要注意的:不要让传进来的arr里面含0这个值
我们把字符串 [a a b c] 认为是字符类型的数组
我们可不可以把一个数组 [17, 29, 5]
这样一个数组理解为字符串去求后缀数组?
也是可以的!
17, 29 算一个字符
所以可以把一个数组理解为字符串, 去求后缀数组
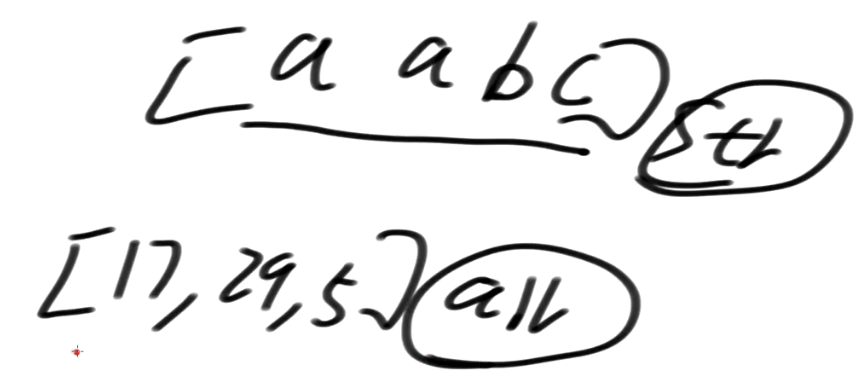

-
为什么arr中不能有 0 这个值?
-
当s1的块跟s2的块 中间是用0来补的
-
如果你arr 有0的值会导致整个模板出错
-
-
如果arr有0的值怎么办?可以做一下转化
- 比如把每个位置+1,+1后的数组的后缀数组排名跟之前的是没有区别的
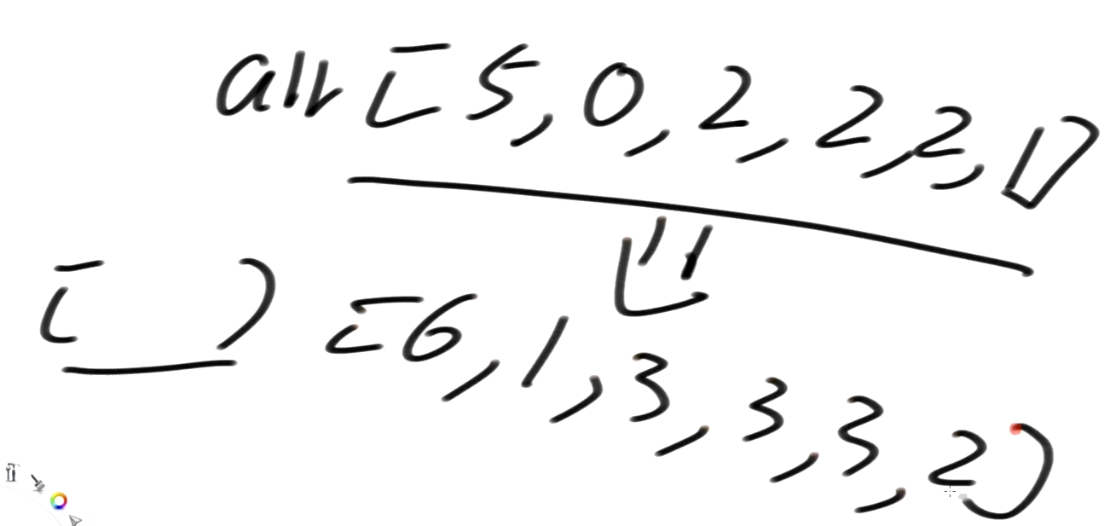






















 1077
1077

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








