线性回归建模
训练,预测
- { ( x ( i ) , y ( i ) ) } \{(x^{(i)},y^{(i)})\} {(x(i),y(i))} ⼀个训练样本, { ( x ( i ) , y ( i ) ) ; i = 1 , ⋯ , N } \{(x^{(i)},y^{(i)});i=1,\cdots ,N\} {(x(i),y(i));i=1,⋯,N} 训练样本集
-
{
(
x
1
(
i
)
,
x
2
(
i
)
,
y
(
i
)
)
}
⟶
{
(
x
(
i
)
,
y
(
i
)
)
}
,
x
(
i
)
=
[
x
1
(
i
)
x
2
(
i
)
]
\{(x_1^{(i)},x_2^{(i)},y^{(i)})\}\longrightarrow\{(\mathbf{x}^{(i)},y^{(i)})\},\mathbf{x}^{(i)}=[\begin{array}{c}x_1^{(i)}\\x_2^{(i)}\end{array}]
{(x1(i),x2(i),y(i))}⟶{(x(i),y(i))},x(i)=[x1(i)x2(i)]
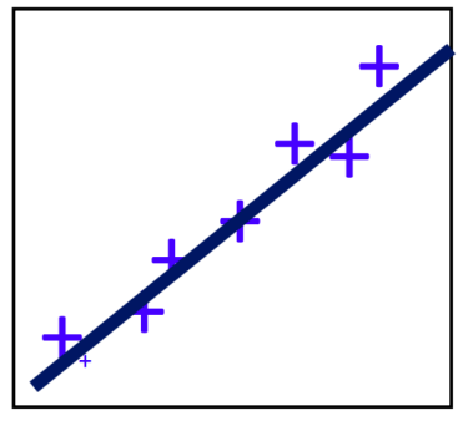
- 试图学习
- 一维: f ( x ) = w x + b f(x)=wx+b f(x)=wx+b 使得 f ( x ( i ) ) ≈ y ( i ) f(x^{(i)}) \approx y^{(i)} f(x(i))≈y(i)
- 多维:
f
(
x
)
=
w
T
x
+
b
f(x)=\mathbf{w}^T \mathbf{x}+b
f(x)=wTx+b 使得
f
(
x
(
i
)
)
≈
y
(
i
)
f(\mathbf{x}^{(i)}) \approx y^{(i)}
f(x(i))≈y(i)
核心问题在于如何学习?
⽆约束优化梯度分析法
无约束优化问题
-
⾃变量为标量的函数 f f f: R → R \mathbf{R} \rightarrow \mathbf{R} R→R
min f ( x ) x ∈ R \min f(x) \quad x \in \mathbf{R} minf(x)x∈R -
⾃变量为标量的函数 f f f: R n → R \mathbf{R}^n \rightarrow \mathbf{R} Rn→R
min f ( x ) x ∈ R n \min f(x) \quad \mathbf{x} \in \mathbf{R}^n minf(x)x∈Rn -
Contour(等高图)
优化问题可能的极值点情况
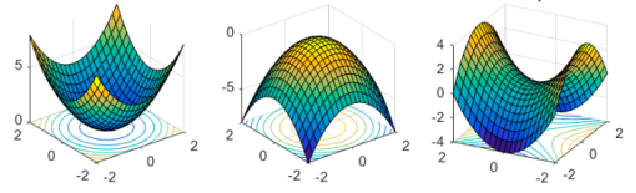
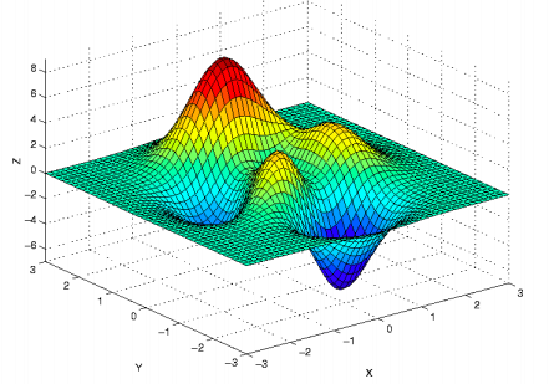
梯度和 Hessian 矩阵
-
一阶导数和梯度(gradient vector)
f ′ ( x ) ; g ( x ) = ∇ f ( x ) = ∂ f ( x ) ∂ x = [ ∂ f ( x ) ∂ x 1 ⋮ ∂ f ( x ) ∂ x n ] f'(x);\mathbf{g}\left(\mathbf{x}\right)=\nabla f(\mathbf{x})=\frac{\partial f(\mathbf{x})}{\partial\mathbf{x}}=\left[\begin{array}{c}\frac{\partial f(\mathbf{x})}{\partial x_1}\\\vdots\\\frac{\partial f(\mathbf{x})}{\partial x_n}\end{array}\right] f′(x);g(x)=∇f(x)=∂x∂f(x)= ∂x1∂f(x)⋮∂xn∂f(x) -
⼆阶导数和 Hessian 矩阵
f ′ ′ ( x ) ; H ( x ) = ∇ 2 f ( x ) = [ ∂ 2 f ( x ) ∂ x 1 2 ∂ 2 f ( x ) ∂ x 1 ∂ x 2 ⋯ ∂ 2 f ( x ) ∂ x 1 ∂ x n ⋯ ∂ 2 f ( x ) ∂ x 2 ∂ x 1 ∂ 2 f ( x ) ∂ x 2 2 ⋱ ∂ 2 f ( x ) ∂ x n ∂ x 1 ∂ 2 f ( x ) ∂ x n ∂ x 2 ∂ 2 f ( x ) ∂ x n 2 ] = ∇ ( ∇ f ( x ) ) T f''(x);\left.\mathbf{H}\left(\mathbf{x}\right)=\nabla^{2}f\left(\mathbf{x}\right)=\left[\begin{array}{ccccc}\frac{\partial^{2}f(\mathbf{x})}{\partial x_{1}^{2}}&\frac{\partial^{2}f(\mathbf{x})}{\partial x_{1}\partial x_{2}}&\cdots&\frac{\partial^{2}f(\mathbf{x})}{\partial x_{1}\partial x_{n}}\cdots\\\frac{\partial^{2}f(\mathbf{x})}{\partial x_{2}\partial x_{1}}&\frac{\partial^{2}f(\mathbf{x})}{\partial x_{2}^{2}}\\&&\ddots\\\frac{\partial^{2}f(\mathbf{x})}{\partial x_{n}\partial x_{1}}&\frac{\partial^{2}f(\mathbf{x})}{\partial x_{n}\partial x_{2}}&&\frac{\partial^{2}f(\mathbf{x})}{\partial x_{n}^{2}}\end{array}\right.\right]=\nabla\left(\nabla f(\mathbf{x})\right)^{T} f′′(x);H(x)=∇2f(x)= ∂x12∂2f(x)∂x2∂x1∂2f(x)∂xn∂x1∂2f(x)∂x1∂x2∂2f(x)∂x22∂2f(x)∂xn∂x2∂2f(x)⋯⋱∂x1∂xn∂2f(x)⋯∂xn2∂2f(x) =∇(∇f(x))T
二次型
给定矩阵
A
∈
R
n
×
n
A \in \mathbf{R}^{n\times n}
A∈Rn×n,函数
x
T
A
x
=
∑
i
=
1
n
x
i
(
A
x
)
i
=
∑
i
=
1
n
x
i
(
∑
j
=
1
n
a
i
j
x
j
)
=
∑
i
=
1
n
∑
j
=
1
n
x
i
x
j
a
i
j
\mathbf{x}^{T}\mathbf{A}\mathbf{x}=\sum_{i=1}^{n}x_{i}\left(\mathbf{A}\mathbf{x}\right)_{i}=\sum_{i=1}^{n}x_{i}\left(\sum_{j=1}^{n}a_{ij}x_{j}\right)=\sum_{i=1}^{n}\sum_{j=1}^{n}x_{i}x_{j}a_{ij}
xTAx=i=1∑nxi(Ax)i=i=1∑nxi(j=1∑naijxj)=i=1∑nj=1∑nxixjaij
被称为⼆次型。
例:对于
f
(
x
)
=
x
1
2
+
x
2
2
+
x
3
2
f\left(\mathbf{x}\right)=x_1^2+x_2^2+x_3^2
f(x)=x12+x22+x32 ,可以写成下面的二次型:
f
(
x
1
,
x
2
,
x
3
)
=
[
x
1
,
x
2
,
x
3
]
[
1
0
0
0
1
0
0
0
1
]
[
x
1
x
2
x
3
]
\begin{aligned} f(x_1,x_2,x_3)=\begin{bmatrix}x_1,x_2,x_3\end{bmatrix}\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix} \end{aligned}
f(x1,x2,x3)=[x1,x2,x3]
100010001
x1x2x3
相关概念:
- 给定对称矩阵 A ∈ R n × n A \in \mathbf{R}^{n\times n} A∈Rn×n ,如果对于所有 x ∈ R n \mathbf{x} \in \mathbf{R}^{n} x∈Rn ,有 x T A x ≥ 0 \mathbf{x}^T\mathbf{A}\mathbf{x} \ge0 xTAx≥0 ,则为 半正定矩阵(positive semidefinite),此时特征值 λ ( A ) ≥ 0 \lambda(\mathbf{A}) \ge 0 λ(A)≥0
- 如果对于所有 x ∈ R n , x ≠ 0 \mathbf{x}\in\mathbb{R}^n,\mathbf{x}\neq\mathbf{0} x∈Rn,x=0,有 x T A x > 0 \mathbf{x}^T\mathbf{A}\mathbf{x} \gt0 xTAx>0,则为正定矩阵(positive definite) .
- 与之对应的还有:负定矩阵、不定矩阵(indefinite)
矩阵求导案例
- 向量 a \mathbf{a} a 和 x \mathbf{x} x 无关,则 ∇ ( a T x ) = a , ∇ 2 ( a T x ) = 0 \nabla\left(\mathbf{a}^T\mathbf{x}\right)=\mathbf{a},\nabla^2\left(\mathbf{a}^T\mathbf{x}\right)=\mathbf{0} ∇(aTx)=a,∇2(aTx)=0
- 对称矩阵矩阵 A \mathbf{A} A 和 x \mathbf{x} x ⽆关,则 ∇ ( x T A x ) = 2 A x , ∇ 2 ( x T A x ) = 2 A \nabla\left(\mathbf{x}^T\mathbf{A}\mathbf{x}\right)=\mathbf{2}\mathbf{A}\mathbf{x}, \nabla^2\left(\mathbf{x}^T\mathbf{A}\mathbf{x}\right)=2\mathbf{A} ∇(xTAx)=2Ax,∇2(xTAx)=2A
- 最小二乘
f ( x ) = ∣ ∣ A x − b ∣ ∣ 2 2 = x T A T A x − 2 b T A x + b T b ∇ f ( x ) = 2 A T A x − 2 A T b \begin{aligned} f(\mathbf{x})& =||\mathbf{Ax}-\mathbf{b}||_2^2 =\mathbf{x}^T\mathbf{A}^T\mathbf{A}\mathbf{x}-2\mathbf{b}^T\mathbf{A}\mathbf{x}+\mathbf{b}^T\mathbf{b} \\ \nabla f(\mathbf{x})&=2\mathbf{A}^T\mathbf{A}\mathbf{x}-2\mathbf{A}^T\mathbf{b} \end{aligned} f(x)∇f(x)=∣∣Ax−b∣∣22=xTATAx−2bTAx+bTb=2ATAx−2ATb
详细求解可以参考《矩阵论》教材
泰勒级数
泰勒级数展开
- 输⼊为标量的泰勒级数展开
f ( x k + δ ) ≈ f ( x k ) + f ′ ( x k ) δ + 1 2 f ′ ′ ( x k ) δ 2 + ⋯ + 1 k ! f k ( x k ) δ k + ⋯ f(x_k+\delta)\thickapprox f(x_k)+f^{\prime}\left(x_k\right)\delta+\frac12f^{\prime\prime}\left(x_k\right)\delta^2+\cdots+\frac1{k!}f^k\left(x_k\right)\delta^k+\cdots f(xk+δ)≈f(xk)+f′(xk)δ+21f′′(xk)δ2+⋯+k!1fk(xk)δk+⋯ - 输⼊为向量的泰勒级数展开
f ( x k + δ ) ≈ f ( x k ) + g T ( x k ) δ + 1 2 δ T H ( x k ) δ f(\mathbf{x}_k+\boldsymbol{\delta})\boldsymbol{\approx}f(\mathbf{x}_k)+\mathbf{g}^T(\mathbf{x}_k)\boldsymbol{\delta}+\frac12\boldsymbol{\delta}^T\mathbf{H}\left(\mathbf{x}_k\right)\boldsymbol{\delta} f(xk+δ)≈f(xk)+gT(xk)δ+21δTH(xk)δ
泰勒级数与极值
-
标量情况
输入为标量的泰勒级数展开
f ( x k + δ ) ≈ f ( x k ) + f ′ ( x k ) δ + 1 2 f ′ ′ ( x k ) δ 2 f(x_k+\delta)\approx f(x_k)+f'\left(x_k\right)\delta+\frac12f''\left(x_k\right)\delta^2 f(xk+δ)≈f(xk)+f′(xk)δ+21f′′(xk)δ2
严格局部极小点: f ( x k + δ ) > f ( x k ) f(x_k+\delta)>f(x_k) f(xk+δ)>f(xk)
称满足 f ′ ( x k ) = 0 f'(x_k)=0 f′(xk)=0 的点为平稳点(候选点); f ′ ( x k ) = 0 f'(x_k)=0 f′(xk)=0 并不能推出为极小值
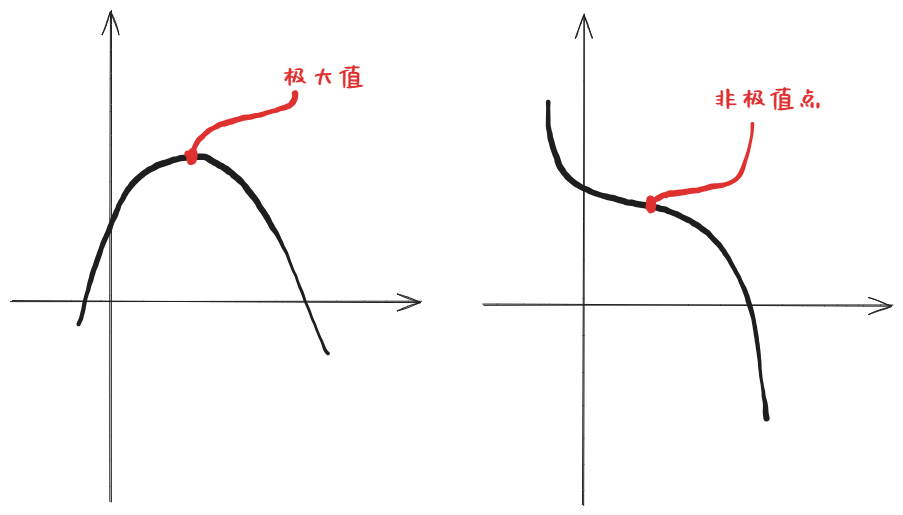
函数在 x k x_k xk 有严格局部极⼩值条件为 f ′ ( x k ) = 0 且 f ′ ′ ( x k ) > 0 f'\left(x_k\right)=0\text{ 且 }f''\left(x_k\right)>0 f′(xk)=0 且 f′′(xk)>0 -
向量情况
输入为向量的泰勒级数展开
f ( x k + δ ) ≈ f ( x k ) + g T ( x k ) δ + 1 2 δ T H ( x k ) δ f(\mathbf{x}_k+\boldsymbol{\delta})\boldsymbol{\approx}f(\mathbf{x}_k)+\mathbf{g}^T(\mathbf{x}_k)\boldsymbol{\delta}+\frac12\boldsymbol{\delta}^T\mathbf{H}\left(\mathbf{x}_k\right)\boldsymbol{\delta} f(xk+δ)≈f(xk)+gT(xk)δ+21δTH(xk)δ
称满足 g ( x k ) = 0 \mathbf{g}\left(\mathbf{x}_k\right)=0 g(xk)=0 的点为平稳点 (候选点),此时如果有 -
H ( x k ) ≻ 0 \mathbf{H}\left(\mathbf{x}_{k}\right)\succ0 H(xk)≻0 , x k \mathbf{x}_k xk 为⼀严格局部极⼩点 (反之,严格局部最⼤点)
-
如果 H ( x k ) \mathbf{H}\left(\mathbf{x}_{k}\right) H(xk) 为不定矩阵,则是⼀个鞍点(saddle point)
梯度为0求解的局限性
计算 f ( x ) = x 4 + sin ( x 2 ) − ln ( x ) e x + 7 f(x) = x^4 + \sin(x^2) - \ln(x)e^x+ 7 f(x)=x4+sin(x2)−ln(x)ex+7 的导数 f ′ ( x ) = 4 x ( 4 − 1 ) + d ( x 2 ) d x cos ( x 2 ) − d ( ln x ) d x e x − ln ( x ) d ( e x ) d x + 0 = 4 x 3 + 2 x cos ( x 2 ) − 1 x e x − ln ( x ) e x \begin{aligned} f^{\prime}(x)& =4x^{(4-1)}+\frac{d\left(x^{2}\right)}{dx}\cos(x^{2})-\frac{d\left(\ln x\right)}{dx}e^{x}-\ln(x)\frac{d\left(e^{x}\right)}{dx}+0 \\ &=4x^3+2x\cos(x^2)-\frac{1}{x}e^x-\ln(x)e^x \end{aligned} f′(x)=4x(4−1)+dxd(x2)cos(x2)−dxd(lnx)ex−ln(x)dxd(ex)+0=4x3+2xcos(x2)−x1ex−ln(x)ex可以看到常规方法无法求解 f ′ ( x ) = 0 f'(x)=0 f′(x)=0 的点
⽆约束优化迭代法
迭代法的基本结构
- step1:选择⼀个初始点,设置⼀个 convergence tolerance ϵ \epsilon ϵ,计数 k = 0 k = 0 k=0
- step2:决定搜索⽅向 d k \mathbf{d}_k dk , 使得函数下降 (核心)
- step3:决定步⻓ α k \alpha_k αk 使得 f ( x k + α k d k ) f(\mathbf{x}_k+\alpha_k\mathbf{d}_k) f(xk+αkdk) 对于 α k ≥ 0 \alpha_k \ge0 αk≥0 最⼩化,构建 x k + 1 = x k + α k d k \mathbf{x}_{k+1}=\mathbf{x}_k+\alpha_k\mathbf{d}_k xk+1=xk+αkdk
- step4:如果 ∥ d k ∥ ≤ ϵ \|\mathbf{d}_k\| \le \epsilon ∥dk∥≤ϵ ,则停⽌输出解 x k + 1 \mathbf{x}_{k+1} xk+1;否则继续重复迭代
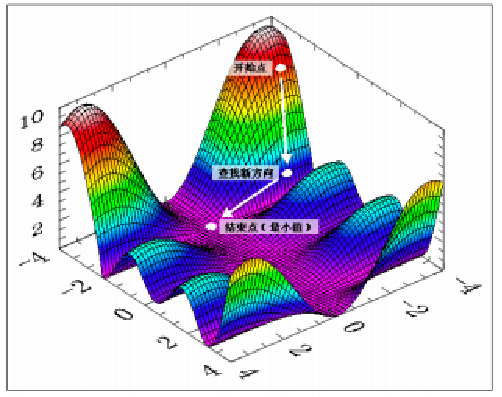
梯度下降法
取
d
k
=
−
g
(
x
k
)
\mathbf{d}_k=-\mathbf{g}(\mathbf{x}_k)
dk=−g(xk),思考为什么这么取?
f
(
x
k
+
d
k
)
≈
f
(
x
k
)
+
g
T
(
x
k
)
d
k
f(\mathbf{x}_k+\mathbf{d}_k)\approx f(\mathbf{x}_k)+\mathbf{g}^T(\mathbf{x}_k) \mathbf{d}_k
f(xk+dk)≈f(xk)+gT(xk)dk
- 需要 f ( x k + d k ) ↓ f(\mathbf{x}_k+\mathbf{d}_k)\downarrow f(xk+dk)↓,则 f ( x k ) f(\mathbf{x}_k) f(xk) 加个负数
- 回忆两个向量的内积,
a
⋅
b
=
a
T
b
=
∥
a
∥
∥
b
∥
cos
θ
\mathbf{a}\cdot\mathbf{b}=\mathbf{a}^T\mathbf{b}=\|a\|\|b\|\cos\theta
a⋅b=aTb=∥a∥∥b∥cosθ
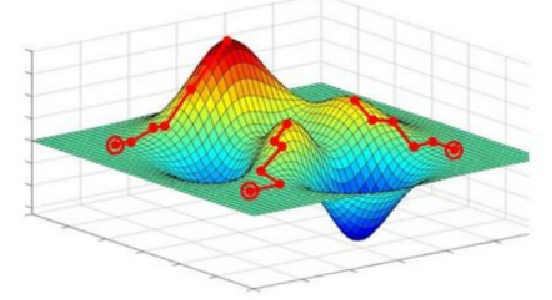
牛顿法
方向选取
方向选取
d
k
=
−
H
−
1
(
x
k
)
g
(
x
k
)
\mathbf{d}_{k}=-\mathbf{H}^{-1}\left(\mathbf{x}_{k}\right)\mathbf{g}\left(\mathbf{x}_{k}\right)
dk=−H−1(xk)g(xk)
方向选取依据
f
(
x
k
+
d
k
)
=
f
(
x
k
)
+
g
T
(
x
k
)
d
k
+
1
2
d
k
T
H
(
x
k
)
d
k
f(\mathbf{x}_k+\mathbf{d}_k)=f(\mathbf{x}_k)+\mathbf{g}^T(\mathbf{x}_k) \mathbf{d}_k+\frac{1}{2}\mathbf{d}_k^T\mathbf{H}\left(\mathbf{x}_k\right)\mathbf{d}_k
f(xk+dk)=f(xk)+gT(xk)dk+21dkTH(xk)dk
令
∂
f
(
x
k
+
d
k
)
∂
d
k
=
0
⇒
g
(
x
k
)
+
H
(
x
k
)
d
k
=
0
\frac{\partial f(\mathbf{x}_k+\mathbf{d}_k)}{\partial\mathbf{d}_k}=\mathbf{0}\Rightarrow\mathbf{g}\left(\mathbf{x}_k\right)+\mathbf{H}\left(\mathbf{x}_k\right)\mathbf{d}_k=\mathbf{0}
∂dk∂f(xk+dk)=0⇒g(xk)+H(xk)dk=0
- 若 Hessian 矩阵正定,则有 d k = − H − 1 ( x k ) g ( x k ) \mathbf{d}_{k}=-\mathbf{H}^{-1}\left(\mathbf{x}_{k}\right)\mathbf{g}\left(\mathbf{x}_{k}\right) dk=−H−1(xk)g(xk)
- 强制要求 Hessian 矩阵正定:参考泰勒展开极值情况讨论
关键点
实际⼯程中 Hessian 矩阵
H
\mathbf{H}
H 很难求,
H
−
1
\mathbf{H}^{-1}
H−1 更加难求
解决思路:
- 修正⽜顿法:当 Hessian 矩阵不是正定矩阵时,可对 Hessian 矩阵进⾏修正:
H
(
x
k
)
+
E
\mathbf{H}(\mathbf{x}_k)+\mathbf{E}
H(xk)+E,典型的⽅法
E
=
δ
I
,
δ
>
0
\mathbf{E}=\delta\mathbf{I}, \delta>0
E=δI,δ>0 很小
+ δ I +\delta\mathbf{I} +δI 可以使得特征值增加,从而使得 H \mathbf{H} H 变为正定 - 拟⽜顿法(Quasi-Newton methods)
拟牛顿法
核心思想
- 统一深度下降法和牛顿法:
d k = − S k g k \mathbf{d}_k=-\mathbf{S}_k\mathbf{g}_k dk=−Skgk - 其中 S k = { I steepest H k − 1 Newton \mathbf{S}_k=\begin{cases}\mathbf{I}&\text{steepest}\\\mathbf{H}_k^{-1}&\text{Newton}\end{cases} Sk={IHk−1steepestNewton
- 不直接求 H k − 1 \mathbf{H}_k^{-1} Hk−1,尝试用一个正定矩阵逼近 H k − 1 \mathbf{H}_k^{-1} Hk−1 (一阶的量慢慢近似二阶的量)
- 定义 δ k = x k + 1 − x k \delta _k= \mathbf{x} _{k+ 1}- \mathbf{x} _k δk=xk+1−xk, γ k = g k + 1 − g k \gamma _k= \mathbf{g} _{k+ 1}- \mathbf{g} _k γk=gk+1−gk
- 需要 S k + 1 γ k = δ k \mathbf{S}_{k+1}\boldsymbol{\gamma}_k=\boldsymbol{\delta}_k Sk+1γk=δk,为什么?
- 但是,只有 δ k \delta_k δk 和 γ k \gamma_k γk 是不可能计算出 S k + 1 \mathbf{S}_{k+1} Sk+1 的,继续用迭代的方法.
DFP
- 给定初始正定对称矩阵 S 0 = I \mathbf{S}_0=\mathbf{I} S0=I
- S k + 1 = S k + Δ S k \mathbf{S} _{k+ 1}= \mathbf{S} _{k}+ \Delta \mathbf{S} _{k} Sk+1=Sk+ΔSk, k = 0 , 1 , ⋯ k= 0, 1, \cdots k=0,1,⋯
-
Δ
S
k
=
α
u
u
T
+
β
v
v
T
\Delta\mathbf{S}_{k}=\alpha\mathbf{uu}^{T}+\beta\mathbf{v}\mathbf{v}^{T}
ΔSk=αuuT+βvvT,因此
S k + 1 = S k + α u u T + β v v T \mathbf{S}_{k+1}=\mathbf{S}_k+\alpha\mathbf{u}\mathbf{u}^T+\beta\mathbf{v}\mathbf{v}^T Sk+1=Sk+αuuT+βvvT - 两边乘以
γ
k
\gamma_k
γk,有
δ
k
=
S
k
γ
k
+
(
α
u
T
γ
k
)
⏟
1
u
+
(
β
v
T
γ
k
)
⏟
−
1
v
=
S
k
γ
k
+
u
−
v
\delta _k= \mathbf{S} _k\gamma _k+\underbrace{\left(\alpha \mathbf{u}^T\boldsymbol{\gamma}_k\right) }_{{\mathrm{1}}}\mathbf{u}+\underbrace{\left(\beta \mathbf{v} ^T\boldsymbol{\gamma}_k\right) }_{{\mathrm{-1}}}\mathbf{v} = \mathbf{S} _k\mathbf{\gamma}_k+\mathbf{u}-\mathbf{v}
δk=Skγk+1
(αuTγk)u+−1
(βvTγk)v=Skγk+u−v
其中, ( u u T γ k ) T = ( γ k T u ) u T = ( u T γ k ) u T \left(\mathbf{uu}^{T}\boldsymbol{\gamma}_k\right)^T=\left(\boldsymbol{\gamma}_k^T\mathbf{u}\right)\mathbf{u}^{T}=(\boldsymbol{\mathbf{u}^{T}\gamma}_k)\mathbf{u}^{T} (uuTγk)T=(γkTu)uT=(uTγk)uT,于是 u u T γ k = ( u T γ k ) ( u T ) T = ( u T γ k ) u \mathbf{uu}^{T}\boldsymbol{\gamma}_k=(\boldsymbol{\mathbf{u}^{T}\gamma}_k)(\mathbf{u}^{T})^T=(\boldsymbol{\mathbf{u}^{T}\gamma}_k)\mathbf{u} uuTγk=(uTγk)(uT)T=(uTγk)u
同理有 v v T γ k = ( v T γ k ) v \mathbf{vv}^{T}\boldsymbol{\gamma}_k=(\boldsymbol{\mathbf{v}^{T}\gamma}_k)\mathbf{v} vvTγk=(vTγk)v - 解出
α
=
1
u
T
γ
k
,
β
=
−
1
v
T
γ
k
\alpha=\frac1{\mathbf{u}^T\boldsymbol{\gamma}_k},\beta=-\frac1{\mathbf{v}^T\boldsymbol{\gamma}_k}
α=uTγk1,β=−vTγk1,且有
u
−
v
=
δ
k
−
S
k
γ
k
\mathbf{u}-\mathbf{v}=\boldsymbol{\delta}_k-\mathbf{S}_k\boldsymbol{\gamma}_k
u−v=δk−Skγk,
不妨令: u = δ k \mathbf{u}=\boldsymbol{\delta}_k u=δk, v = S k γ k \mathbf{v}=\mathbf{S}_k\boldsymbol{\gamma}_k v=Skγk,于是 α = 1 δ k T γ k \alpha=\frac1{\boldsymbol{\delta}_k^T\boldsymbol{\gamma}_k} α=δkTγk1, β = − 1 γ k T S k T γ k = − 1 γ k T S k γ k \beta=-\frac1{\boldsymbol{\gamma}_k^T\mathbf{S}_k^T\boldsymbol{\gamma}_k}=-\frac1{\boldsymbol{\gamma}_k^T\mathbf{S}_k\boldsymbol{\gamma}_k} β=−γkTSkTγk1=−γkTSkγk1
将 u , v , α , β \mathbf{u},\mathbf{v},\alpha,\beta u,v,α,β 带回得到 S k + 1 = S k + δ k δ k T δ k T γ k − S k γ k γ k T S k γ k T S k γ k \mathbf{S}_{k+1}=\mathbf{S}_k+\frac{\delta_k\delta_k^T}{\delta_k^T\gamma_k}-\frac{\mathbf{S}_k\gamma_k\gamma_k^T\mathbf{S}_k}{\gamma_k^T\mathbf{S}_k\gamma_k} Sk+1=Sk+δkTγkδkδkT−γkTSkγkSkγkγkTSk - Davidion-Feltcher-Powell(DFP) 更新公式
S k + 1 = S k + δ k δ k T δ k T γ k − S k γ k γ k T S k γ k T S k γ k \mathbf{S}_{k+1}=\mathbf{S}_k+\frac{\delta_k\delta_k^T}{\delta_k^T\gamma_k}-\frac{\mathbf{S}_k\gamma_k\gamma_k^T\mathbf{S}_k}{\gamma_k^T\mathbf{S}_k\gamma_k} Sk+1=Sk+δkTγkδkδkT−γkTSkγkSkγkγkTSk
BFGS
Broyden-Fletcher-Goldfarb-Shanno (BFGS):
S
0
=
I
S_0=\mathbf{I}
S0=I
S
k
+
1
=
S
k
+
(
1
+
γ
k
T
S
k
γ
k
δ
k
T
γ
k
)
δ
k
δ
k
T
δ
k
T
γ
k
−
δ
k
γ
k
T
S
k
+
S
k
γ
k
δ
k
T
δ
k
T
γ
k
\mathbf{S}_{k+1}=\mathbf{S}_k+\left(1+\frac{\gamma_k^T\mathbf{S}_k\gamma_k}{\delta_k^T\gamma_k}\right)\frac{\delta_k\delta_k^T}{\delta_k^T\gamma_k}-\frac{\delta_k\gamma_k^T\mathbf{S}_k+\mathbf{S}_k\gamma_k\delta_k^T}{\delta_k^T\gamma_k}
Sk+1=Sk+(1+δkTγkγkTSkγk)δkTγkδkδkT−δkTγkδkγkTSk+SkγkδkT
步长求取
- 方式1:每次迭代固定步⻓,实际中最常⽤,例如 α k = α = 0.1 \alpha_k=\alpha=0.1 αk=α=0.1
- 方式2:求导:例如 f ( x ) = x T A x + 2 b T x + c f(\mathbf{x})=\mathbf{x}^T\mathbf{A}\mathbf{x}+2\mathbf{b}^T\mathbf{x}+c f(x)=xTAx+2bTx+c,需要解 min α ≥ 0 f ( x + α d ) \min_{\alpha\geq0}f(\mathbf{x}+\alpha\mathbf{d}) minα≥0f(x+αd) 则 h ( α ) = f ( x + α d ) h\left(\alpha\right)=f(\mathbf{x}+\alpha\mathbf{d}) h(α)=f(x+αd) ,则有 ∂ h ( α ) ∂ α = 0 ⇒ α = − d T ∇ f ( x ) 2 d T A d \frac{\partial h(\alpha)}{\partial\alpha}=0\Rightarrow\alpha=-\frac{\mathbf{d}^{T}\nabla f(\mathbf{x})}{2\mathbf{d}^{T}\mathbf{Ad}} ∂α∂h(α)=0⇒α=−2dTAddT∇f(x)
- 方式3:不精确的线搜索和 Armijo 条件
f ( x k + α d k ) < f ( x k ) + c 1 α g T ( x k ) d k f(\mathbf{x}_k+\alpha\mathbf{d}_k)<f(\mathbf{x}_k)+c_1\alpha\mathbf{g}^T(\mathbf{x}_k) \mathbf{d}_k f(xk+αdk)<f(xk)+c1αgT(xk)dk
设置 c 1 = 1 0 − 4 c_1=10^{-4} c1=10−4 ,具体参考 NumericalOptimization。先从 α = 1 \alpha=1 α=1 搜,如果 Armijo 条件不满⾜,设置回调因⼦ β ∈ ( 0 , 1 ) \beta\in(0,1) β∈(0,1),将步⻓下调⾄ α = β α \alpha=\beta\alpha α=βα。如果还不满足,继续回调(backtracking line search),从而保证步长不至于太小。
线性回归求解
解法 1:利⽤梯度等于 0
- 试图学习: f ( x ) = w T x + b f(\mathbf{x})=\mathbf{w}^T\mathbf{x}+b f(x)=wTx+b 使得 f ( x ( i ) ) ≈ y ( i ) f\big(\mathbf{x}^{(i)}\big)\approx y^{(i)} f(x(i))≈y(i)
- 未知
w
‾
=
[
w
b
]
\overline{\mathbf{w}}=\left[\begin{array}{c}\mathbf{w}\\b\end{array}\right]
w=[wb],已知
X
=
[
x
(
1
)
T
1
⋮
⋮
x
(
N
)
T
1
]
N
×
(
d
+
1
)
\mathbf{X}=\left[\begin{array}{cc}\mathbf{x}^{(1)T}&1\\\vdots&\vdots\\\mathbf{x}^{(N)T}&1\end{array}\right]_{N\times(d+1)}
X=
x(1)T⋮x(N)T1⋮1
N×(d+1),则有
y ≈ X w ‾ \mathrm{y}\approx\mathrm{X}\overline{\mathrm{w}} y≈Xw - 损失函数
∣
∣
y
−
X
w
‾
∣
∣
2
2
||\mathbf{y}-\mathbf{X}\overline{\mathbf{w}}||_2^2
∣∣y−Xw∣∣22 ,求解
min ∣ ∣ y − X w ‾ ∣ ∣ 2 2 \min||\mathbf{y}-\mathbf{X}\overline{\mathbf{w}}||_2^2 min∣∣y−Xw∣∣22 - g ( w ‾ ) = 0 ⇒ 2 X T ( X w ‾ − y ) = 0 ⇒ w ‾ ∗ = ( X T X ) − 1 X T y g\left(\overline{\mathbf{w}}\right)=0\Rightarrow2\mathbf{X}^T\left(\mathbf{X}\overline{\mathbf{w}}-\mathbf{y}\right)=0\Rightarrow\overline{\mathbf{w}}^*=\left(\mathbf{X}^T\mathbf{X}\right)^{-1}\mathbf{X}^T\mathbf{y} g(w)=0⇒2XT(Xw−y)=0⇒w∗=(XTX)−1XTy
- 正则化
解法2:梯度下降
- 梯度下降法
g ( w ‾ ) = 2 X T ( X w ‾ − y ) = 2 ∑ i = 1 N x ( i ) ( w T x ( i ) − y ( i ) ) w ‾ ← w ‾ − α g ( w ‾ ) \begin{aligned} \mathbf{g}\left(\overline{\mathbf{w}}\right)& =2\mathbf{X}^{T}(\mathbf{X}\overline{\mathbf{w}}-\mathbf{y}) \\ &=2\sum_{i=1}^N\mathbf{x}^{(i)}\left(\mathbf{w}^T\mathbf{x}^{(i)}-y^{(i)}\right) \\ &\overline{\mathrm{w}}\leftarrow\overline{\mathrm{w}}-\alpha\mathbf{g}\left(\overline{\mathrm{w}}\right) \end{aligned} g(w)=2XT(Xw−y)=2i=1∑Nx(i)(wTx(i)−y(i))w←w−αg(w) - 随机梯度下降法(实际中很有用)
{ i = 1 : N , 2 x ( i ) ( w T x ( i ) − y ( i ) ) } \left\{i=1:N, 2\mathbf{x}^{(i)}\left(\mathbf{w}^T\mathbf{x}^{(i)}-y^{(i)}\right)\right\} {i=1:N,2x(i)(wTx(i)−y(i))}
























 7365
7365











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








