动态规划与贪心算法之课程安排问题

动态规划算法与贪心算法之课程安排问题

1. 动态规划算法之课程安排
   问题：教务处给某一个教室安排课程，有很多老师都想来这个教室教授他们各自的课。假如第$i$位老师讲的第$A_i$门课程，课程开始时间$S_i$,结束时间为$F_i$。那么教务处的老师就要利用这个时间如何安排课程，使得来这间教室上课的人数最多？
   举个例子：
   
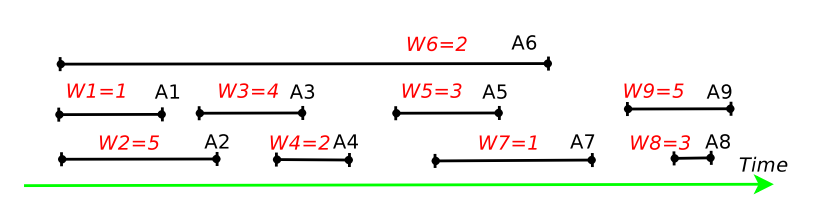
   最底下为时间轴，每条黑线代表一门课程。我们用$W$表示该课程有多少学生。我们看教务处安排最多有多少人来该教室上课。
   分析：课程太多我无从下手。看能不能分成子问题求解。先DandC，然后DP。我们把求解过程看出一系列决策过程，在每个步骤我们都要选一门课程。假装我们已经拿到了最优决策方案，我现在就想知道最优解中最后一个决策到底是什么？也就是$A_n$ 你是选了还是