Size Balanced Tree(SBT树)整理

不想用treap和Splay，那就用SB树把，哈哈，其实它一点也SB，厉害着呢。

先膜拜一下作者陈启峰。Orz

以下内容由我搜集整理得来。

一、BST及其局限性

二叉查找树（Binary Search Tree），也称有序二叉树（ordered binary tree）,排序二叉树（sorted binary tree），是指一棵空树或者具有下列性质的二叉树：
1.若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
2.任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
3.任意节点的左、右子树也分别为二叉查找树。
4.没有键值相等的节点（no duplicate nodes）。

二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低。 为O(log n)

但是，缺点是若待插入的序列是有序的，那么它会退化成单链表！这样查询时间将会为O（n）！

解决办法有很多改进版的二叉查找树可以使树高为O(logn),如SBT,AVL,红黑树,treap等

红黑树和AVL比较复杂，不太适合在算法竞赛中使用。

基本平衡思想如下：

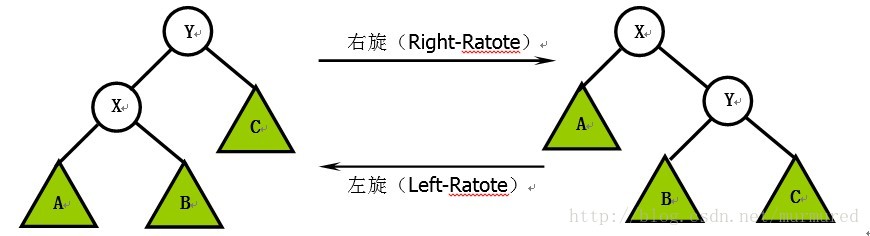
右旋的伪代码

右旋操作假定左儿子存在。

Right-Rotate(t)
 k ← left[t]
 left[t] ← right[k]
 right[k] ← t
 s[k] ← s[t]
 s[t] ← s[left[t]] + s[right[t]] + 1
 t ← k

左旋的伪代码

 左旋操作假定右儿子存在。

Left-Rotate(t)
 k ← right[t]
 right[t] ← left[k]
 left[k] ← t
 s[k] ← s[t]
 s[t] ← s[left[t]] + s[right[t]] + 1
 t ← k

二、SBT

Size Balanced Tree(简称SBT)是一种平衡二叉搜索树，它通过子树的大小s[t]来维持平衡性质。它支持很多动态操作，并且都能够在O(log n)的时间内完成。

为了下面方便讨论，

我们设

left [T] : 结点 T 的左儿子
right [T] : 结点 T 的右儿子
s [T] : 以T为根的子树的结点个数（大小））

SBT为什么能保持平衡？

  因为 对于SBT的每一个结点 t,有如下性质：

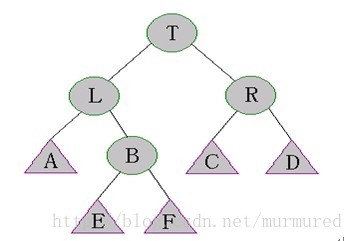
    性质(a) s[ right[t] ]≥s[ left [ left[ t ] ] ], s[ right [ left[t] ] ]
   性质(b) s[ left[t] ]≥s[right[ right[t] ] ], s[ left[ right[t] ] ]
即.每棵子树的大小不小于其兄弟的子树大小。(对于数组来实现树不熟悉的童鞋，请把s[ left [ left[ t ] ] ] 翻译为s[ t->left->left ] 同样的，s[ right [ left[t] ] ]翻译为s[ t->left->right ] ）

如上图有s[A],s[B]≤s[R]和s[C],s[D] ≤s[L]

1.平衡维护mantain

在执行完简单的插入之后，性质a或性质b可能就不满足了，于是我们需要调整SBT。

Ｍaintain (T) 用于修复以 T 为根的 SBT 。由于性质(a)和(b)是对称的，下面仅讨论对性质(a)的修复。

Case 1: s[ Left[ Left[ T ] ]>s[ Right[ T ] ] 

在下图中，就是说 s[A]>s[R]

首先执行右旋（Right-Rotate (T)）可得

有可能旋转后的树仍然不是SBT,需要再次执行Maintain(T)

由于L的右儿子发生了变化，因此需要执行Maintain(L)

也就是说，这种情况先执行一次Right-Rotate (T)，接着执行Maintain (T) 保证T为SBT，然后执行Maintain(L)，保证L为SBT

Case 2: s[ right[ left[ t ] ]>s[ right[ t ] ]  

在下图中，也就是说 s[B]>s[R]

先执行左旋Left-Rotate(L)。如下图

执行右旋Right-Rotate(T)，如下图：

接着执行Maintain (L) 和Maintain (T)，来保证L和T是SBT

同理执行Maintain (B)

Case 3：s[ right[ right[ t ] ] ]>s[ left[ t ] ]
 这个和case 1是对称的。。。。

Case 4：s[ left[ right[ t ] ] ]>s[ left[ t ] ]

这个和case 2是对称的。。

可写出C++代码如下,感觉比伪代码好看。。。

void matain(int &t)  
    {  
        if(size[ left[ left[t] ] ] > size[ right[t] ] )  
        {  
            right_rotate(t);  
            matain(right[t]);  
            matain(t);  
        }  
        else if( size[ right[ left[t] ] ]>size[ right[t] ] )  
        {  
            left_rotate(left[t]);  
            right_rotate(t);  
            matain(left[t]);  
            matain(right[t]);  
            matain(t);  
        }  
        else if(size[ right[ right[t] ] ]>size[ left[t] ])  
        {  
            left_rotate(t);  
            matain(left[t]);  
            matain(t);  
        }  
        else if(size[ left[ right[t] ] ]>size[ left[t] ])  
        {  
            right_rotate(right[t]);  
            left_rotate(t);  
            matain(left[t]);  
            matain(right[t]);  
            matain(t);  
        }  
}

有了维护操作后，接下来的步奏就很简单了。

2.插入insert

Insert (t,v)
 If t=0 then
   t ← NEW-NODE(v)
 Else
   s[t] ← s[t]+1
   If v<key[t] then
     Simple-Insert(left[t],v)
   Else
     Simple-Insert(right[t],v)
   Maintain(t,v≥key[t])

3.删除delete

如果没有找到要删除的结点，那么就删除最后一个访问的结点并记录。

Delete (t,v)
  s[t] ←s[t]－1
  If (v=key[t])or(v<key[t])and(left[t]=0)or(v>key[t])and(right[t]=0) then
    Delete ←key[t]
    If (left[t]=0)or(right[t]=0) then
      t ←left[t]+right[t]
    Else
      key[t] ←Delete(left[t],v[t]+1)
  Else
    If v<key[t] then
      Delete(left[t],v)
    Else
      Delete(right[t],v)
  Maintain(t,false)
  Maintain(t,true)

由于SBT的性质（结点t的关键字比其左子树中所有结点的关键字都大，比其右子树中所有的关键字都小），理解下面的算法非常容易。

4.Select操作

返回在第k位置上的结点(即返回根为t的树中排名为k的结点。)。显然它包括了取大（Maximum）和取小（Minimun），取大等价于Select(t,1)，取小等价于Select(t,s[t])。

Select(t,k)
       If k=s[left[t]]+1 then
              return key[t]
       If k<=s[left[t]] then
              return Select(left[t],k)
       Else
              return Select(right[t],k-1-s[left[t]])

5.Rank操作

返回v在以t为根的树中的排名，也就是比v小的那棵树的大小（Size）加一。

Rank(t,v)
       If t=0 then
              return 1
       If v<=key[t] then
              return rank(left[t],v)
       Else
              return s[left[t]]+1+rank(right[t],v)

6.其他的

证明什么的就不说啦，有兴趣的可以看作者原论文。

结论就是：

1.SBT的高度为O(logn)

2.Maintain的平摊运行时间是：O（1）

一个用SBT树解决第K大元素的例子

数据结构与算法实验题 10.1 神谕者 （ http://blog.csdn.net/murmured/article/details/16945287）方法4