Halo2学习笔记——背景资料之Elliptic curves（5）

1. 引言

基于有限域构建的椭圆曲线，是另一重要的密码学工具。

采用椭圆曲线，是因为其可提供a cryptographic group，即在group内，DLP（discrete logarithm problem）是困难的。

有多种方式来定义曲线方程$E({\mathbb{F}}_p)$，但是Halo2中，定义的${\mathbb{F}}_p$为255-bit field，满足方程式$y^2=x^3+b$成立的所有解集（${\mathbb{F}}_p$-rational points）$(x,y)$，称为“affine coordinates”。
这些${\mathbb{F}}_p$-rational points 和 “point at infinity” $\mathcal{O}$（作为group identity） 一起，都是group内的元素。传统地，都将elliptic curve groups写成加法态的。

由上图可知：“Three points on a line sum to zero, which is the point at infinity”。

相应的group addition law很简单：若求$P+Q$，则将$P$和$Q$连线，其与曲线上交叉第第三个点为$R$，将$R$的$y$坐标求反，即为$P+Q=(R_x,-R_y)$。
对于$P=Q$的情况，称为point doubling，需特殊处理：即找到该点的切线，然后将该切线与曲线的交叉点$y$坐标求反即为结果。
有$(R_x,-R_y)+(R_x,R_y)=\mathcal{O}$。

The ability to add and double points naturally gives us a way to scale them by integers, called scalars。
曲线上点的个数称为group order。group order为prime $q$，则可将scalars认为是elements of a scalar field ${\mathbb{F}}_q$。

椭圆曲线，如果设计得当的话，具有重要的安全属性：
已知2个random elements $G,H\in E({\mathbb{F}}_p)$，找到$a$使得$[a]G=H$ 被认为是computationally infeasible with classical computers。这也称为是elliptic curve discrete log assumption。

若椭圆曲线group $\mathbb{G}$ 具有prime order $q$（Halo2中使用的曲线满足该要求）则其为finite cyclic group，其为isomorphic to $\mathbb{Z}/q\mathbb{Z}$，或者等价为，isomorphic to the scalar field ${\mathbb{F}}_q$。
每个可能的generator $G$都满足isomorphism，即在scalar 端存在某值，其为precisely the discrete log of the corresponding group element with respect to $G$。对于密码学安全的曲线，the isomorphism is hard to compute in the $\mathbb{G}\to {\mathbb{F}}_q$ direction，因为elliptic curve discrete log problem is hard。

有时，相比于group elements，借助scalars的isomorphism思想更有助于理解group-based cryptographic protocols and algorithms。

2. Curve arithmetic

2.1 Point addition and point doubling

详细可参看《Elliptic Curves Number Theory and Cryptography（second edition）》第2.2节可知，有：

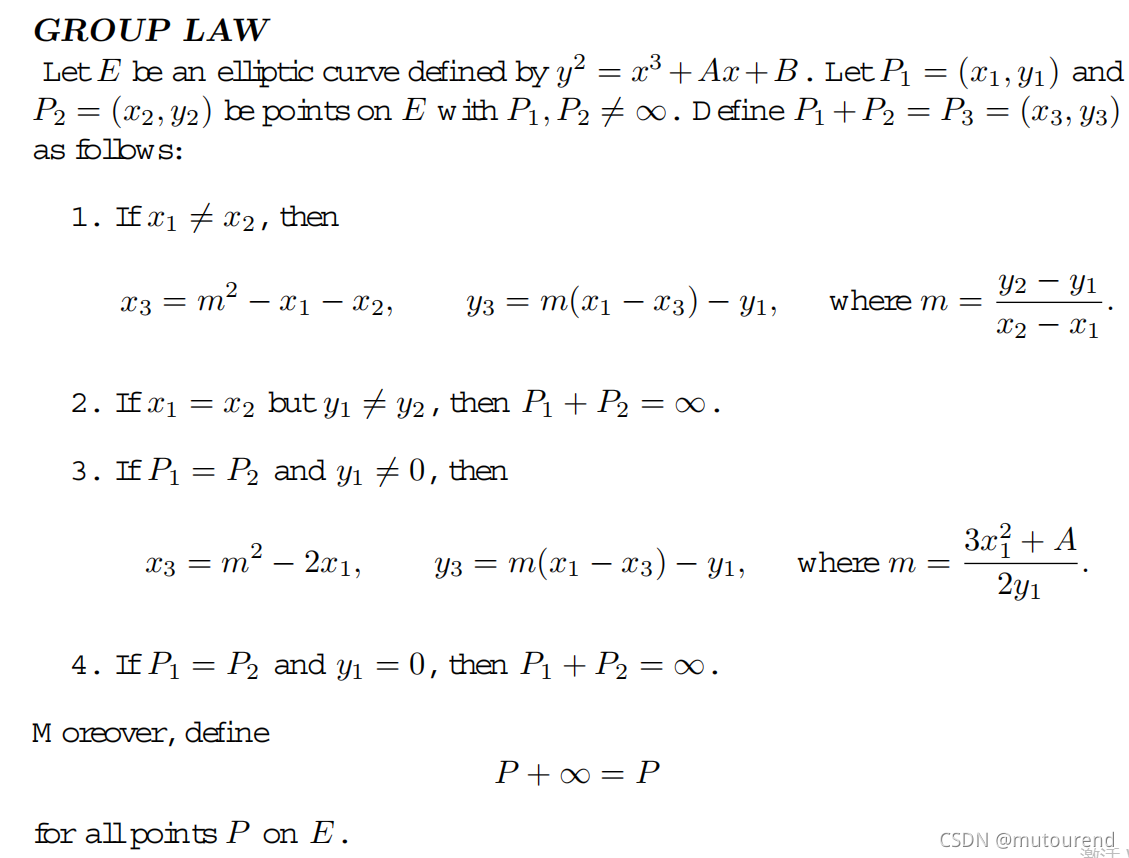
对于$y^2=x^3+b$ curve，对应有：

• Point addition：
  求$(x_0,y_0)+(x_1,y_1)=(x_2,y_2)$，其中$x_0\ne x_1$，有：
  $\lambda =\frac{y_1-y_0}{x_1-x_0}$
  $y_2=\lambda (x_0-x_2)-y_0$
  $x_2={\lambda }^2-x_0-x_1$
• Point doubling：
  求$(x_1,y_1)=(x_0,y_0)+(x_0,y_0)$，有：
  $\lambda =\frac{dy}{dx}=\frac{3x^2}{2y}$
  $y_1=\lambda (x_0-x_1)-y_0$
  $x_1={\lambda }^2-2x_0$

根据Renes等人2015年论文《Complete addition formulas for prime order elliptic curves》中，存在有效的公式，可将point addition和point doubling同时处理。

2.2 Projective coordinates

2.1节中的point doubling中，存在昂贵的inversion of $2y$。为了避免倒数运算，而且实际并不立即需要单个curve operation的resulting point的actual affine $(x^{\prime },y^{\prime })$坐标。

对于$y^2=x^3+b$ curve，引入第三个坐标系$Z$，扩展为：
$Z^3{y}^2=Z^3{x}^3+Z^{3}b$

当$Z=1$时，对应的就是$y^2=x^3+b$ curve。
令$X=xZ,Y=yZ$ 且 $Z\ne 0$，则有相应的homogenous projective curve为：
$Y^{2}Z=X^3+Z^{3}b$

当$Z\ne 0$时，根据$(X,Y,Z)$ 计算 $(X/Z,Y/Z)$即为相应的affine coordinate。
当$Z=0$时，表示为the point at infinity $O=(0:1:0)$。

通常来说，Projective coordinates通常（而不总是）比 affine coordinates 效率要高。例外的情况是：

• 可使用Montgomery’s trick时
• 当乘法运算和倒数运算的开销相当时

在projective coordinates下对point $(X,Y,Z)=(xZ,yZ,Z)$进行double运算，有：
$\lambda =\frac{3x^2}{2y}=\frac{3(X/Z{)}^2}{2(Y/Z)}=\frac{3X^2}{2YZ}$

double运算结果$(x,y)+(x,y)=(x^{\prime },y^{\prime })$可表示为：
$x^{\prime }={\lambda }^2-2x={\lambda }^2-\frac{X}{Z}=\frac{18X^{4}YZ-16X{Y}^3{Z}^2}{8Y^3{Z}^3}$
$y^{\prime }=\lambda (x-x^{\prime })-y=\frac{12X^3{Y}^{2}Z-8Y^4{Z}^2-27X^6+24X^3{Y}^{2}Z}{8Y^3{Z}^3}$

为此，可令$Z=8Y^3{Z}^3，X=18X^{4}YZ-16X{Y}^3{Z}^2，Y=12X^3{Y}^{2}Z-8Y^4{Z}^2-27X^6+24X^3{Y}^{2}Z$，从而有$X/Z=x^{\prime },Y/Z=y^{\prime }$。
这样就可完全避免倒数运算。

注意：

• 除projective coordinate和affine coordinate之外，还有Jacobian coordiante，令$(x,y)=(x{Z}^2,y{Z}^3,Z)$，即将curve rescaled by $Z^6$ 而不是 $Z^3$。
• 在homogenous projective coordinate下，比较2个curve point $(X_1,Y_1,Z_1)$ 和 $(X_2,Y_2,Z_2)$是否相同，即验证$X_1{Z}_2=X_2{Z}_1$和$Y_1{Z}_2=Y_2{Z}_1$是否成立。

3. Curve endomorphisms

假设${\mathbb{F}}_p$ 有 a primitive cube root of unity，或换句话说，有$3|p-1$，使得an element ${\zeta }_p$可生成a 3-order multiplicative subgroup。
则椭圆曲线$y^2=x^3+b$上的point $(x,y)$ 存在2个cousin points：【因为${\zeta }_p^3=1$】
$({\zeta }_{p}x,y)$和$({\zeta }_p^{2}x,y)$。

使用map $(x,y)\mapsto ({\zeta }_{p}x,y)$即为 应用an endomorphism over the curve。

详细的机制很复杂，但是当curve有prime $q$个points（即具有prime order），实现endomorphism的方式为：

• multiply the point by a scalar in ${\mathbb{F}}_q$，该scalar值为a primitive cube root ${\zeta }_q$ in the scalar field。

4. Curve point compression

对于curve上的point $P=(x,y)$，其negation为$-P=(x,-y)$ 也在curve上。为了唯一确定某point，需将其$x$坐标 和 $y$坐标的正负标记符 一起encode。

根据Fields 章节中描述，可将field element的最低有效位（LSB，Least Significant Bit）作为其正负标记符，因为其additive inverse will always have the opposite LSB。

将$y$坐标的LSB标记为sign。

Pallas curve和Vesta curve分别基于${\mathbb{F}}_p$和${\mathbb{F}}_q$域，每个element都可以255 bits表示，若用32-byte来表示，正好有一个bit是未使用的。可将$y$坐标的sign bit存入表示$x$坐标的32-byte的最高位：

         <----------------------------------- x --------------------------------->
Enc(P) = [_ _ _ _ _ _ _ _] [_ _ _ _ _ _ _ _] ... [_ _ _ _ _ _ _ _] [_ _ _ _ _ _ _ sign]
          ^                <------------------------------------->                 ^
         LSB                              30 bytes                                MSB

“point at infinity” $\mathcal{O}$ 为group identity，不存在相应的affine $(x,y)$表示。
但是，对于Pallas和Vesta curve来说，不存在$x=0$或$y=0$的point。
因此，使用"fake" affine coordinates $(0,0)$来encode $\mathcal{O}$，从而对应为all-zeroes 32-byte array。

4.1 Deserialization

当需要对压缩的curve point进行反序列化时，首先需读取最高有效位作为ysign，为$y$坐标的正负标记符。然后将该位置为0，来恢复原始的$x$坐标。

若$x=0,y=0$，则返回“point at infinity” $\mathcal{O}$。
否则，计算$y=\sqrt{x^3+b}$，读取$y$的最低有效位sign，若$sign=ysign$，则返回point $(x,y)$，否则返回$(x,-y)$。

5. Cycles of curves

令$E_p$为elliptic curve over finite field ${\mathbb{F}}_p$，其中$p$为prime，将其表示为$E_p/{\mathbb{F}}_p$。
group of points of $E_p$ over ${\mathbb{F}}_p$，具有order $q=\#E({\mathbb{F}}_p)$，将${\mathbb{F}}_p$称为base field，${\mathbb{F}}_q$称为scalar field。

Halo2将instantiate proof system over the elliptic curve $E_p/{\mathbb{F}}_p$，需prove statements about ${\mathbb{F}}_q$-arithmetic circuit satisfiability。

QA：
curve为$E_p$ over ${\mathbb{F}}_p$，为何其arithmetic circuit为基于${\mathbb{F}}_q$而不是${\mathbb{F}}_p$的呢？
因为proof system通常是基于encodings of the scalars in the circuit（或更准确的说，commitments to polynomials whose coefficients are scalars）。这些scalars是基于${\mathbb{F}}_q$的，而其encodings或commitments则是elliptic curve point in $E_p/{\mathbb{F}}_p$。

但是，大多数Verifier的arithmetic computations是基于base field ${\mathbb{F}}_p$的，因此可高效表示为an ${\mathbb{F}}_p$-arithmetic circuit。

QA：
为何说Verifier的计算主要是基于${\mathbb{F}}_p$的呢？
因为Halo2中Verifier实际需使用circuit的output information来运行group operations。类似point doubling和point addition的group operations，都是arithmetic in ${\mathbb{F}}_p$，因为这些point的坐标值都是in ${\mathbb{F}}_p$的。

构建另一条scalar field为${\mathbb{F}}_p$曲线的主要目的是：

• 具有an ${\mathbb{F}}_p$-arithmetic circuit，可高效verify proofs from the first curve。
  此外，若第二条曲线的base field为$E_q/{\mathbb{F}}_q$，则将generate proofs that could be efficiently verified in the first curve’s ${\mathbb{F}}_q$-arithmetic circuit。换句话说，可instantiate a second proof system over $E_q{\mathbb{F}}_q$，从而形成a 2-cycle with the first：
  

5.1 Halo2中使用的Pallas-Vesta curves

Halo2中使用的Pallas-Vesta curves 详细参见：
https://github.com/zcash/pasta

6. Hashing to curves

有时，需能根据某输入，生成elliptic curve $E_p/{\mathbb{F}}_p$上的一个随机point，而没人知道具体的discrete logarithm关系。

详细见：
Internet draft on Hashing to Elliptic Curves

根据效率和安全性要求，在Internet draft中使用的框架函数主要有：

• hash_to_field：输入为a byte sequence，将该输入map为a element in the base field ${\mathbb{F}}_p$。
• map_to_curve：输入为${\mathbb{F}}_p$ element，输出为$E_p$ point。

6.1 Simplied SWU

详细可参见Wahby和Boneh 2019年论文《Fast and simple constant-time hashing to the BLS12-381 elliptic curve》。

参考资料

[1] Halo2 背景资料之Elliptic curves