[从头学数学] 第205节 初等数论初步

最新推荐文章于 2021-04-04 03:53:26 发布
最新推荐文章于 2021-04-04 03:53:26 发布
阅读量1.4k 收藏 4
点赞数 1
分类专栏： 从头学数学 从头学数学
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/mwsister/article/details/51344310
版权
在星历2016年05月08日，银河系厄尔斯星球的中华帝国江南行省，工程师阿伟与机器小伟共同深入研究了初等数论的基础知识。
摘要由CSDN通过智能技术生成
剧情提要：
[机器小伟]在[工程师阿伟]的陪同下进入了[九转金丹]之第七转的修炼。
这次要研究的是[初等数论初步]。

正剧开始：


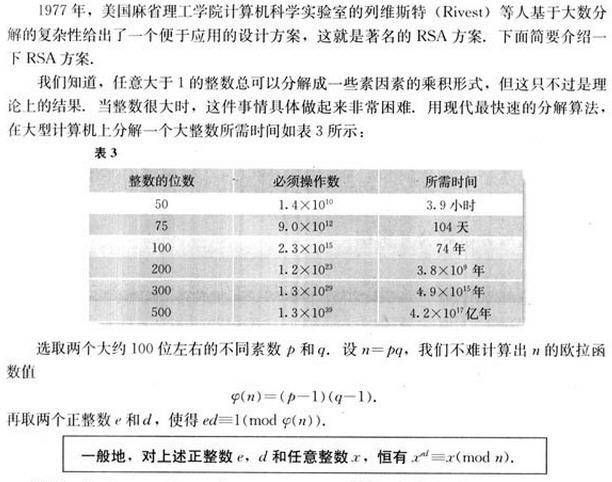
星历2016年05月08日 10:05:37, 银河系厄尔斯星球中华帝国江南行省。
[工程师阿伟]正在和[机器小伟]一起研究[初等数论初步]。











<span style="font-size:18px;">710316能被3整除
710316能被9整除
710316 不能 被11整除
710316 不能 被7整除

#根据规律判整除性
#其实并不实用，只是说明一下规律
def tmp():
    number = 710316;
    array =  numberArray(number);
    size = len(array);

    #被11整除
    array_odd = array[0:size:2];
    array_even = array[1:size:2];

    #被7整除
    array_last3 = number%1000;
    array_front = (number-array_last3)//1000;

    #判断被3整除
    if sum(array)%3==0:
        print('{0}能被3整除'.format(number));
    else:
        print('{0} 不能 被3整除'.format(number));

    #判断被9整除
    if sum(array)%9==0:
        print('{0}能被9整除'.format(number));
    else:
        print('{0} 不能 被9整除'.format(number));

    #判断被11整除
    if (sum(array_odd)-sum(array_even))%11 == 0:
        print('{0}能被11整除'.format(number));
    else:
        print('{0} 不能 被11整除'.format(number));
        
    #判断被7整除
    if (array_last3 - array_front)%7==0:
        print('{0}能被7整除'.format(number));
    else:
        print('{0} 不能 被7整除'.format(number));
		
#把一个整数的各位数字放入数组
#由个位往高位排列
def numberArray(number):
    array = [];
    bit = len(str(number));

    for i in range(bit):
        array.append(number%10);
        number//=10;

    #array.reverse();
    
    return array;</span>


 







<span style="font-size:18px;">#判断一个数是否质数  
def prime(num):  
    if (num < 2):  
        return False;  
      
    sqr = int(math.sqrt(num))+1;  
  
    for i in range(2, sqr):  
        if (num%i==0):  
            return False;  
  
    return True; </span>


 



<span style="font-size:18px;">#最大公约数
def gcd(m, n):    
    m, n = max(m, n), min(m, n);    
    i = 1;    
    while n:    
        print('step', i, ': ', m, n);    
        i += 1;    
        m, n = n, m % n    
            
    return m</span>


 


<span style="font-size:18px;">#最小公倍数
def lcm(m, n):
    return m*n/gcd(m, n);</span>


 

<span style="font-size:18px;">>>> 
2625.0

print(lcm(375, 105));</span>


 


<span style="font-size:18px;">#分解质因数  
def primeFactor(num, lists):  
    if (num < 2):  
        lists.append(num);  
        return lists;  
    elif (prime(num) == True):  
        lists.append(num);  
        return lists;  
    else:      
        sqr = int(math.sqrt(num))+1;  
        i = 2;  
  
        while i <= sqr:  
            if (num % i == 0 and prime(i) == True):  
                lists.append(i);  
                num = num//i;  
                break;  
              
            i+=1;  
        return primeFactor(num, lists); </span>


 



<span style="font-size:18px;">>>> 
720 = 2 * 2 * 2 * 2 * 3 * 3 * 5
152 = 2 * 2 * 2 * 19
8
13680.0

def tmp2():
    number = [720, 152];

    for j in range(len(number)):
        factors = primeFactor(number[j], []);
        count = len(factors);
        s = str(number[j])+' = ';
        
        for i in range(count):
            s += str(factors[i]);
            if (i < count-1):
                s += ' * ';

        print(s);
        
    print(gcd(720,152));
    print(lcm(720, 152));</span>


 






















<span style="font-size:18px;">>>> 
21的欧拉函数值φ(21) = 12.0

def tmp3(number):
    print('{0}的欧拉函数值φ({0}) = {1}'.format(number, round(eulerPhi(number),3)))
	
#欧拉函数
def eulerPhi(number):
    factors = set(primeFactor(number, []));

    factors = sorted(factors);    
    #print(factors);

    phi = number;

    for i in range(len(factors)):
        phi *= (1-1/factors[i]);

    return phi;</span>


 

<span style="font-size:18px;">>>> 
25的欧拉函数值φ(25) = 20.0


def tmp4():
    for i in range(1, 21):
        if (18**i)%25==1:
            print(i);
            break;</span>


 





<span style="font-size:18px;">>>> 
[4.0, 9.0, 14.0]

def tmp5():
    result = [];
    mod = 15;
    remain = 6;
    quotient = 9;
        
    for i in range(1, 20):        
        x = (mod*i + remain)/quotient;
        if abs((int(x))-x)< 1e-6:
            result.append(x);

        if x > mod:
            break;

    print(result);</span>


 



<span style="font-size:18px;">>>> 
[9.0]

#例6
def tmp5():
    result = [];
    mod = 74;
    remain = 1;
    quotient = 33;
        
    for i in range(1, 20):        
        x = (mod*i + remain)/quotient;
        if abs((int(x))-x)< 1e-6:
            result.append(x);

        if x > mod:
            break;

    print(result);</span>


 











<span style="font-size:18px;">		var s = [
			'f(a)=e, f(b)=f, f(c)=g',
			'a=-1,  e=2;',
			'b=0,  f=3;',
			'c=1,  g=6;',
			'f(x) = 2(x-0)(x-1)/(-1)/(-2)',
			' +3(x+1)(x-1)/(1)/(-1)',
			' +6(x+1)(x-0)/(2)/(1)',
		];</span>

 
<span style="font-size:18px;">[58, 238, 418, 598, 778, 958, 1138, 1318, 1498]

#孙子定理的变通
def tmp6():
    remain = [2, 3, 4];
    mod = [4, 5, 9];
    count = len(mod);

    multi = 1;
    for i in range(count):
        multi *= mod[i];

    #直接遍历这个范围
    bound = sum(remain)*multi+1;
    result = [];

    for i in range(1, bound):
        for j in range(count):
            if i%mod[j]!=remain[j]:
                break;
            if j >= count-1:
                result.append(i);
    
    print(result);</span>


 

<span style="font-size:18px;">[282, 975, 1668, 2361, 3054, 3747, 4440, 5133, 5826, 6519, 7212, 7905]

#孙子定理的变通
def tmp6():
    #模数
    mod = [7, 9, 11];
    #余数
    remain = [2, 3, 7];
    
    count = len(mod);

    multi = 1;
    for i in range(count):
        multi *= mod[i];

    #直接遍历这个范围
    bound = sum(remain)*multi+1;
    result = [];

    for i in range(1, bound):
        for j in range(count):
            if i%mod[j]!=remain[j]:
                break;
            if j >= count-1:
                result.append(i);
    
    print(result);</span>


 

<span style="font-size:18px;">[2111, 4421, 6731, 9041, 11351, 13661, 15971, 18281, 20591, 22901, 25211, 27521, 29831, 32141, 34451, 36761, 39071, 41381, 43691, 46001]

#韩信点兵

#孙子定理的变通
def tmp6():
    #模数
    mod = [5, 6, 7, 11];
    #余数
    remain = [1, 5, 4, 10];
    
    count = len(mod);

    multi = 1;
    for i in range(count):
        multi *= mod[i];

    #直接遍历这个范围
    bound = sum(remain)*multi+1;
    result = [];

    for i in range(1, bound):
        for j in range(count):
            if i%mod[j]!=remain[j]:
                break;
            if j >= count-1:
                result.append(i);
    
    print(result);</span>


 



















<span style="font-size:18px;">2 30 68
5 25 70
8 20 72
11 15 74
14 10 76
17 5 78
20 0 80

#百马百瓦
def tmp8():
    a = 33;
    b = 50;
    c = 200;
    result = [];
    
    for i in range(a+1):
        for j in range(b+1):
            for k in range(c+1):
                if (abs(((i*3 + j*2 + k*0.5) - 100)) < 1e-6) and i+j+k == 100:
                    print(i, j, k);</span>


 



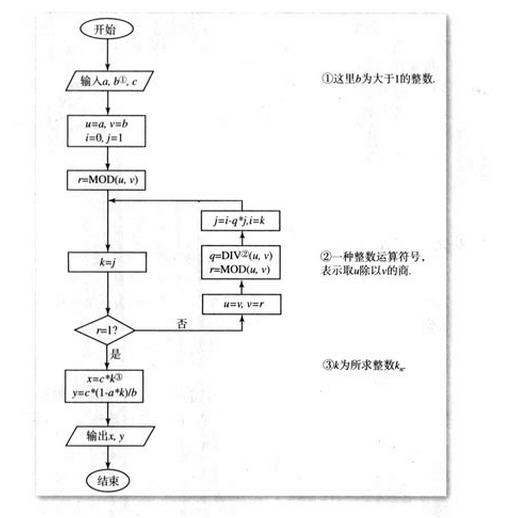
<span style="font-size:18px;">#不定方程
def tmp7():
    #ax + by  = c
    #b为大于1的整数
    a, b, c = 3, 2, 5;

    u, v, i, j = a, b, 0, 1;
    r = u%v;
    k = j;
    
    while r!=1:
        u, v = v, r;
        q = u//v;
        r = u%v;
        j = i-q*j;
        i = k;
        k = j;

    x = c*k;
    y = c*(1-a*k)/b;

    print(x, y);</span>


 


>>> 
-34 6.0

#不定方程
def tmp7():
    #ax + by  = c
    #b为大于1的整数
    a, b, c = 13, 74, 2;

    u, v, i, j = a, b, 0, 1;
    r = u%v;
    k = j;
    
    while r!=1:
        u, v = v, r;
        q = u//v;
        r = u%v;
        j = i-q*j;
        i = k;
        k = j;

    x = c*k;
    y = c*(1-a*k)/b;

    print(x, y);






本节到此结束，欲知后事如何，请看下回分解。

mwsister
关注
专栏目录
初等数论习题解答第三版
10-14
初等数论是数学的基础课之一，对于学习数学的学生来说极为重要。初等数论习题解答第三版为广东石油化工学院编写的习题解答，涵盖了初等数论的主要内容。本资源摘要信息将对初等数论习题解答第三版进行详细的解读和...
专题 初等数论初步从入门到放弃
weixin_44577381的博客
07-26 991
文章目录1、整数的整除整除的基本性质带余除法（欧几里得除法）2、素数素数的相关性质素数的判断素数的筛法埃拉托斯特尼筛法（埃氏筛法）算法原理代码线性筛（欧拉筛法）算法原理正确性证明（即所有合数都会被标记）3、最大公因数与最小公倍数裴蜀定理（贝祖定理）4、同余5、剩余类及其运算6、费马小定理7、同余方程8、快速幂9、中国剩余定理与BSGS 1、整数的整除 定义1 设a,ba,ba,b为整数，b≠0b ...
初等数论初步——最大公因数
dianshu1593的博客
07-15 1890
一、定义 定义：给定两个整数a，b,必有公共的因数，叫做它们的公因数，当a,b不全部为0时，在有限个公因数中最大的那个叫做a、b的最大公因数，记作(a,b) 二、一种方法——辗转相除法 描述：设a,b为任意两个整数，且b不为0，应用带余除法，以b除a,得到商q1,余数r1；如果余数r1不为0，以r1除b，得到商q2，余数r2;如果r2不等于0，以r2除r1,如此继续下去，在有限个除...
oracle特殊数据类型,Oracle的特殊数据类型
weixin_42510271的博客
04-04 287
1.%TYPE允许用户动态地将数据库中某一列的数据类型与PL/SQL中某个变量关联。语法如下:variable_name table.column%TYPE2.%ROWTYPE允许用户定义单一的变量,该变量包含数据库表的每一列的多个变量。语法规则如下:variable_name table%ROWTYPE一旦定义了这种变量,就可以使用 如下的方式来访问各个列:row_variable.column...
oracle 如何输出 table(number_array),sql – Oracle中匿名TABLE/VARRAY类型示例详解
weixin_42498163的博客
04-03 186
前言本文主要介绍的是关于sql Oracle匿名TABLE/VARRAY类型的相关内容，在Oracle中,我有时会创建一些这样的结构?显然,我可以为上述声明我自己的类型.我可以在TABLE和VARRAY之间进行选择.例如：?在这种特殊情况下,另一个解决方案是写东西?但是我可能会有更复杂的例子,我真的需要一个TABLE / VARRAY类型.那么如果我的SQL在一个未知的系统上运行,我不能创建类型,...
oracle 如何输出 table(number_array),oracle table()函数用法
weixin_36382073的博客
04-03 293
PL/sql表---table()函数用法/*PL/sql表---table()函数用法：利用table()函数，我们可以将PL/sql返回的结果集代替table。oracle内存表在查询和报表的时候用的比较多，它的速度相对物理表要快几十倍。simple example：1、table()结合数组：*/create or replace type t_test as object(id integ...
初中数学竞赛专家讲座初等数论-2021.01.15.pdf
01-20
### 初等数论知识点 #### 例题解析 **例题1** - **题目**: 从1到100中任取51个数，证明一定存在两个整数，其中一个数是另一个数的倍数。 - **解析**: 这个问题可以通过鸽巢原理来解决。考虑到任何两个相邻的数之间...
102.《高中数学竞赛专题讲座 初等数论》边红平本书主编
09-29
102.《高中数学竞赛专题讲座 初等数论》边红平本书主编
初等数论100例.pdf
03-10
很抱歉，但您提供的文件信息中，【部分内容】并没有具体的初等数论相关知识点，仅重复出现了指向E书联盟的链接。因此，无法直接从这部分内容中提取知识点。由于无法查看实际的文档内容，我将基于标题“初等数论100例...
初等数论PPT(2020.09.04).rar
09-04
初等数论是一门研究整数性质的数学分支，它主要关注整数的...总的来说，这个压缩包提供了丰富的数学和计算机科学知识，不仅对于学习初等数论的学员，也对那些对算法、编程和组合数学感兴趣的人提供了宝贵的学习资源。
《初等数论》习题集及答案
07-04
自学考的同志啊！看了不后悔啊！这可是我辛辛苦苦找到的哦！分享分享啊
初等数论初步
qq_42421714的博客
02-15 330
文章目录判断质数判断1~n范围内的质数整数的唯一分解最小公倍数和最大公约数（gcd&amp;amp;&amp;amp;lcm）$\forall$n的约数个数$\forall$n的约数之和同余欧拉函数 初学数论 学得十分肤浅 判断质数 for(i = 2;i * i &amp;lt;= n;i++) if(n % i == 0) { able = 1; break; } 判...
初等数论初步——算数基本定理
dianshu1593的博客
07-16 641
算数基本定理 任何大于1的整数都可以分解成素因数乘积的形式，并且，如果不计分解式中素因数的次序，这种分解式是唯一的 1）证明： 存在性：对于大于1的整数你，如果n不是素数，我们可以将n分解成一个素数和某个大于1的整数a的乘积；如果a是素数,则过程停止，如果a不是素数，又可以将a分解成一个素数和某个大于1的整数b的乘积；如果b是素数,则过程停止，如果b不是素数，又可以将b分解成一个素...
Number、String、Array的相互转换
jianchibuxie0的博客
08-12 480
Number——>String：用Number.toString（） String——>Number：用parseInt（String） String——>Array：用String.split（“ ”） Array——>String：用Array.jion（“ ”）
String类型、Number类型、Object类型、Array类型的基本方法总结
文♥记
03-20 3778
一、String类型 String类型可以使用String构造函数来创建： var stringVal = new String("Hello welcome"); 1.字符方法 charAt()和charCodeAt()方法用于访问字符串中的特定字符，接收一个参数（基于0的字符位置），需要注意的是他们返回的值。 var stringVal = "Welcome to her...
SDAU暑假训练第一天----------数论（1）（2018/7/30）
于衡的博客
07-30 409
今天暑假训练就正式开始了，这个周是学习数论的相关知识。今天主要看了数论中整除的相关内容 话不多说，进入正题 目录 话不多说，进入正题 整除 （一）基本概念： （二）性质： （三）特殊数字的整除性质： 补充整除知识：用“截尾法”判断整除性。 GCD与LCM GCD 欧几里得  更相减损术 辗转相除法与更相减损术的比较 GCD的二进制写法（stein算法） LCM 扩展...
python 内置函数
weixin_30632089的博客
11-20 90
chr 数字转换字母 r = chr(65)print(r) ord字母转换数字n = ord("A")print(n) random 函数 import random li = []for i in range(6): temp = random.randrange(65, 91) c = chr(temp) li.append(c)result = " ".joi...
美修大数据：2022母婴洗护品类洞察报告(2).pdf
最新发布
11-03
美修大数据：2022母婴洗护品类洞察报告(2).pdf
VB程序实例-图片剪切.zip
11-03
VB程序实例-图片剪切.zip
利用Sage探索初等数论：质数、密码学与椭圆曲线
第四部分，4.1节至4.6节介绍了二次互反律，这是数论中一个深奥且重要的定律。这部分内容不仅给出了二次互反律的陈述，还提供了多个证明方法，如欧拉准则和高斯和的证明，以及求解平方根的方法。 最后，5.1节至5.4节...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值