【计算机体系结构】计算机体系结构(6) 并行处理技术(2) 多处理机-CSDN博客

本文链接：https://blog.csdn.net/myRealization/article/details/122880593

文章目录

6.5 多处理机

6.5 多处理机

多处理机是指具有两台以上的处理机，在操作系统控制下通过共享的主存或输入/输出子系统或高速通信网络进行通信。使用多处理机的目的：一是用多台处理机，进行多任务处理，协同求解一个大而复杂的问题来提高速度，二是依靠冗余的处理机及其重组，提高系统的可靠性、适应性和可用性。

因为应用目的和结构不同，多处理机可以有同构型、异构型和分布型三种。本节只介绍以「实现作业与任务间并行、提高速度」为目标的多处理机。

6.5.1 多处理机的特点

多处理机属多指令流多数据流 MIMD 系统，与单指令流多数据流 SIMD 系统的并行处理机相比，具有如下特点：

(1) 结构灵活性

SIMD 并行处理机的结构主要是针对向量、数组处理设计的，只能开发其数据的并行性。在 MIMD 多处理机中存在有多指令流，因而在不同的处理单元上可执行不同的指令，可适应多样的算法，结构应更灵活多变，以实现复杂的机间互连，避免争用共享的硬件资源。

(2) 程序并行性

SIMD 并行处理机实现操作级并行，一条指令即可对整个数组同时处理，并行性存在于指令内部，识别比较容易。MIMD 多处理机并行性存在于指令外部，表现于多个任务的并行，加上系统要求通用，使程序并行性的识别较难，必须利用算法、程序语言、编译、操作系统以及指令、硬件等多种途径，挖掘各种潜在的并行性。

(3) 并行任务派生

SIMD 并行处理机由指令反映数据间能否并行计算，并启动多个处理单元并行工作。而 MIMD 多处理机需要有专门指令或语句，指明程序中各程序段的并发关系，控制它们并发执行，使一个任务执行时可派生出另一些任务与它并行执行。因此，多处理机运行效率较并行处理机要高一些。

(4) 进程同步

SIMD 并行处理机实现指令内数据操作的并行，所有活跃的处理单元在同一控制器控制下同时执行同一条指令，工作自然是同步的。MIMD 多处理机实现的是指令、任务、作业的并行，不同处理机执行的是不同指令，工作进度可以不一致。但若并发程序之间有数据相关或控制依赖，就要采取同步措施，使并发进程能按所需的顺序执行。

(5) 资源分配和任务调度

SIMD 并行处理机主要执行向量、数组运算，处理单元数目是固定的。程序员编程时，用屏蔽手段设置处理单元的活跃状态，就可改变实际参加并行执行的处理单元数。MIMD 多处理机执行并发任务，需用处理机的个数没有固定要求，各个处理机进入或退出任务、以及所需资源变化的情况要复杂得多。这就需要解决好资源分配和任务调度，让处理机的负荷均衡，尽可能提高系统硬件资源的利用率；管理和保护好各处理机、进程共享的公用单元，防止系统死锁。

6.5.2 多处理机的分类

多处理机系统在系统结构上可分为紧耦合和松耦合系统。

1. 紧耦合多处理机系统

紧耦合 Tightly Coupled 多处理机系统是通过共享主存实现处理机之间的相互通信的。在这种系统中，通常处理机的数目是有限的，因为主要受两个方面的约束：一是因采用共享主存进行通信，所以当处理机数目增多时，将导致访问主存资源冲突的概率增大，使系统效率下降；二是处理机与主存之间互连网络的带宽有限，当处理机数目增多后，互连网络将成为系统性能的瓶颈。

为了改善访问主存所发生的冲突，常采用如下一些方法：
① 采用多模块交叉访问的主存系统。交叉度越大，访问主存冲突概率就越小，但必须注意，如何恰当地将数据分配到各个存储模块中去。
② 使每个处理机拥有一个小容量的局部存储器，用来存放频繁使用的核心代码等，以减少对主存访问次数。
③ 使每个处理机都有一个 Cache ，以减少对主存访问。但必须注意 Cache 与主存之间、以及各个 Cache 之间的数据的一致性。

图6.36示出了一个典型的紧耦合多处理机系统。系统由 $m$ 个存储模块， $p$ 个处理机和 $d$ 个 I/O 通道组成，由三个互连网络 $\textrm{PMIN}$ （处理机—主存）、 $\textrm{PPIN}$ （处理机—处理机）和 $\textrm{PIOIN}$ （处理机—I/O 通道）将它们连接起来。
在这里插入图片描述
紧耦合系统按所用处理机类型是否相同及对称，又可分为同构或异构、以及对称或非对称形式，常见的组合是同构对称型多处理机系统、异构非对称型多处理机系统。

(1) 同构对称型多处理机系统

Sequent公司生产的 Balance 多处理机系统就是同构对称型的，它的结构如图
6.37所示。CPU模块数可在 $2 ～ 32$ 之间选择，存储器模块可在 $1 ～ 6$ 之间选择。每个CPU模块由 80386 微处理器、Weitek 1167 浮点运算器以及 64K Cache 组成，每个 MEM 模块由 $8 M B$ （可扩充到 $40 M B$ ）及一个存储器控制器组成。上述CPU模块和 MEM 模块均与系统总线相连。系统总线还通过总线适配器与 Ethernet , SCSI 相连，或是通过磁盘控制器与磁盘相连。此外，它还借助总线 Multibus 和总线适配器与远程网相连。
在这里插入图片描述

我国由国家智能中心研制的“曙光一号”是一个由 $4$ 个CPU组成的同构对称型
多处理机系统，CPU采用Motorola公司生产的 MC88100 及两个 Cache MC88200 芯片组成，标准主存容量为 $64 M B$ （可扩展到 $768 M B$ ），用高速局部总线将 $4$ 个CPU及主存连接起来。此外，还通过总线适配器和接口与远程网（X.25）、局网（Ethernet）以及 SCSI 接口相连。

(2) 异构非对称型多处理机系统

图6.38中示出了这种异构非对称型多处理机系统。其中主CPU中所用的微处
理机可不同于从机中的微处理机。从机中 CIOP 处理机与字符外部设备相连，BIOP 与数组外设相连，NIOP 及 GIOP 分别为网络及图形处理机，ACOP 为向量加速处理机。
在这里插入图片描述

2. 松耦合多处理机系统

松耦合 Loosely Coupled 多处理机系统，它是通过消息传递方式来实现处理机间的相互通信，而每个处理机是由「一个独立性较强的计算机模块」组成的，该模块由处理器、局部存储器、I/O 设备以及与消息传递系统相连接的接口所组成。图6.39示出了松耦合多处理机系统的框图。
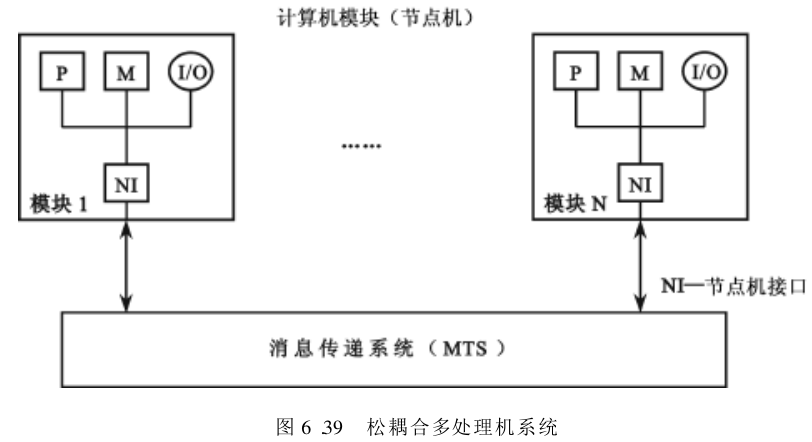
在这里插入图片描述

由于每个计算机模块中的局部存储器容量较大，故在运算时所需的绝大部分指令和数据取自局部存储器。当不同模块上运行的进程间需要通信时，可通过「节点接口及消息传递系统」进行消息交换。由于相互间的耦合程度是很松散的，因此称为松耦合多处理机系统。在有的松耦合多处理机系统中，计算机模块本身就是一个完全独立的计算机，因此有时也将松耦合多处理机系统称为松耦合多计算机系统。

松耦合多处理机系统可分为非层次式和层次式两种结构。图6.39中的多机系统结构即是非层次式的。其中的网络接口 Network interface, NI 通常是由通道和仲裁开关 Channel and Arbiter Switch, CAS 组成，当有两个或多个计算机模块同时请求访问消息传递系统 Message Transfer System, MTS 时，CAS 进行仲裁。

6.5.3 多处理机间的互连方式

多处理机系统中，对机间互连方式的要求比 SIMD 计算机要高一些，具体表现在以下三个方面：一是互连模式要灵活多样，以适应机间通信模式的多样性；二是应能适应机间通信的不规则性，实现无冲突连接；三是要求互连网络具有高带宽和低成本。

多处理机系统中常用的互连模式有以下几种。

1. 总线互连方式

总线互连方式是多机系统中实现互连的最简单的一种结构形式。多个处理机、存储器模块和 I/O 部件，通过各自的接口部件与一条公用系统总线相连。欲传送的信息以分时或多路转换方式，在系统中的主控器及宿控器之间传送。在多处理机系统总线中，潜在的总线主控器主要是处理机或计算机模块，宿控器可以是处理机或计算机模块，也可以是存储器模块或 I/O 部件。

总线互连方式的优点是简单、价廉和模块可扩展性灵活。主要缺点是：可靠性较差，一旦总线失效将导致整个系统失效；带宽较窄，因此可连接到总线的部件、模块和处理机数有限，过多的总线负载将导致主控器争用总线的加剧和信息传送时间的加长，从而使整个系统性能下降。

多处理机系统总线的工作步骤为：首先，由各个潜在主控器争用总线使用权；其次，被选中的主控器及宿控器相连；最后，信息按一定规约，通过总线在一对主控和宿控器间进行传送，必要时也可由一个主控器以广播方式向多个宿控器发送信息。

与单处理机总线一样，用总线带宽来衡量多处理机总线性能的好坏。为增加带宽，通常采用的方法是：用优质电缆组成总线，以提高总线速率；增加总线数，如采用双总线或多总线结构、系统总线加局部总线结构、层次式总线结构。

在总线互连方式中，为了解决多个潜在主控器同时争用总线问题，需由系统总线仲裁机构——总线仲裁器进行裁决，以确定哪个请求源可以使用系统总线。仲裁器一般由某种仲裁算法和相应的硬件构成。仲裁算法的好坏对系统性能有较大影响。

下面介绍常用的仲裁算法。

静态优先级算法：它为每个连到总线上的处理机（或计算机模块）分配一个惟一的固定优先级。当多个处理机同时请求使用系统总线时，仲裁器使优先级最高的申请者使用总线。通常用串行链接方式确定优先级，因而越靠近仲裁器的处理机，它的优先级就越高。这种算法的优点是算法简单，容易实现。缺点是优先级低的处理机将很少有机会使用总线。
平等算法：通常以轮转方式，将总线按固定大小的时间片，依次供各处理机使用。该算法的优点是算法较简单，且能保证各处理机有均等机会使用总线，缺点是平均等待时间较长。此外，若所轮到的处理机不用总线时，将造成总线带宽的浪费。
动态优先级算法：根据总线使用情况和相应规则，动态地改变连接到总线上的多处理机的优先级。例如，近期最少使用 LRU 算法，它将最高的优先级分配给「在最长时间间隔内未使用总线的处理机」。循环菊花链 Rotating Daisy Chain, RDC 算法，则根据「离最后一次使用总线的处理机所处位置的远近」分配优先级。它将总线、准用线按某一方向接成闭环，刚使用总线的处理机的优先级最低，而离它越近的处理机的优先级越高。该算法的优点是兼顾了前两种算法的优点，即有较短的平均等待时间；并可使系统中的各处理机，有更均等的机会使用总线。缺点是控制逻辑较为复杂。
先来先服务算法：这是一种理想算法。它不是按优先级选择主控器，因而具有最好的均等性，该算法是性能最好的仲裁算法，但实现困难。该算法的作用是提供一种标准以衡量其他算法的好坏。

上述的各种仲裁算法，通常用集中方式实现，即统一由一个仲裁器实现仲裁算法。此时，对于总线的请求和允许使用信号，可采用如下三种实现方式：一是请求线共享，而允许使用线则用串行菊花链方式连接。二是请求和允许使用线都采用分离独立的线。三是采用前两种混合方式。

上述各种仲裁算法也可采用分布方式实现，此时的仲裁硬件被分布到各个处理机中。它的工作方式如下：每个潜在总线主控器分配一个惟一的优先号，提出申请的主控器将自己的优先号，送往共享请求/有效线进行逻辑或操作，得到一个合成优先号，然后提出申请的各个主控器，将自己的优先号与合成号相比较。比合成优先号小的申请者将自动撤销申请。这样剩下获得总线使用权的，必将是具有最高优先号的处理机。分布式仲裁算法的优点是有较高的可靠性。

分布式仲裁器的工作过程如下：

首先，通过请求线，接收来自各处理机发来的使用总线请求；
然后，由仲裁器加以仲裁，并以串行链接或并行分离方式，向选中的处理机，在总线准用线上发出总线有效信号；
最后，由选中处理机通过总线忙控制线，向其他处理机表明总线已被占用。
当主控处理机使用总线传送信息后，便撤销总线忙信号，此后，仲裁器便可再去响应选择其他处理机对总线的请求。

多处理机总线的发展趋向是实行标准化，已有一些总线标准支持多处理机系统，常用的有 VME 总线和 Multibus II 总线等。前者以异步方式传送信息，后者则以同步方式传送信息。当用总线结构互连多处理机时，应尽量采用总线标准；如因需要必须采用专用总线时，也应通过总线适配器与标准总线相连，惟此，各种按总线标准设计的外围设备，才能方便地与多处理机系统相连。

标准总线一般都带有仲裁器，如 VME 总线仲裁器采用集中式结构，而 Multibus II 和 Futurebus 总线仲裁器则采用分布式结构。这些标准总线一般都支持优先和均等混合仲裁算法，以适应多处理机系统需要。对外围部件使用优先仲裁算法，而对其他处理机则使用均等仲裁算法，以使各处理机有较均等机会使用系统总线。

总线互连方式虽有简单、价廉的优点，但其吞吐率是固定有限的。当有更多的处理机连到总线上时，就会使总线的工作速度大为降低。而当处理机数多到某一程度时，总线将会出现饱和状态，因此，总线互连方式不适宜连接过多的处理机。

2. 环形互连方式

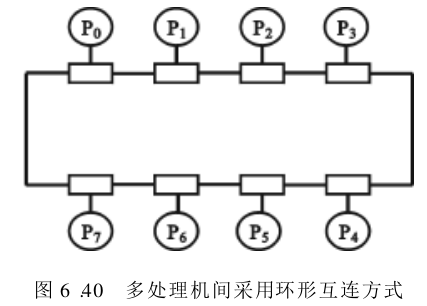
为保持总线互连方式的优点，同时又能克服其不足，可以考虑构造一种逻辑总
线，让各台处理机之间点点相连成环状，称环形互连，如图6.40所示。在这种多处理机上，信息的传递过程是由发送进程将信息送到环上，经环形网络不断向下一台处理机传递，直到此信息又回到发送者处为止。
在这里插入图片描述

发送信息的处理机拥有一个惟一的令牌 Token ，它是普通传送的信息中不会
出现的特定标记。同时，只能有一台处理机可持有这个令牌。发送者在发送信息时，环上其他处理机都处于接收信息的状态。发送者一旦将信息发送完，就向环上播送令牌。其他处理机依次传递此信息和令牌，并根据需要可接收信息。如果某台处理机想要发送信息，在收到令牌后，不再将令牌传向下一台处理机，此时这台处理机就可以通过环形网络发送信息了。如果各处理机都不发送信息，令牌就在环形网络上不断循环传递，直至某台处理机需要发送信息为止。

由于环形互连是点点连接，不是总线式连接，其物理参数容易得到控制，非常适合于有高通信带宽的光纤通信。光纤通信是很难用在总线互连方式系统上的。环形互连的缺点是，信息在每个接口处都会有一个单位的传输延迟，当互连的处理机数增加时，环中的信息传输延迟将增大。但与总线式互连不同的是，即使网上处理机机数很多、通信负荷很重，都不会出现像总线互连那样使系统带宽急剧下降的情况，系统的带宽仍保持一个高值。这是因为令牌环网可看成是一种周期短、延迟长的流水线。

只要计算时能够保持流水线处于满负荷流动，让各处理机的计算和传输重叠进行，发送者在发送完全部信息后，不用等回收到此信息，就将其持有的令牌向下传递给新的发送者，有效带宽就可以得到最充分的利用。
反之，若只有当原来的信息都不在环上传递时，才能发送新的信息，那么就会与「在二次不同操作之间需要排空流水线」的做法类似（？）。这样，随着环形网上处理机数的增加，网络的带宽会严重降低，造成系统效率急剧下降。

3. 交叉开关互连方式

交叉开关互连由一组二维阵列的开关组成，它将横向的 $P$ 台处理机及纵向的模数为 $m$ 的存储器连接起来。阵列中的总线数等于所有处理机数 $P$ 与存储器模数 $m$ 之和。只要 $m \geq P$ ，就必然可以使每个处理机都能有一套总线、与某一个存储器模块相连，从而可以大大加宽带宽。

这是一种无阻塞的互连方式，与总线互连中采用时分制不同，它是采用空间分配机制。图6.41中示出了这种纵横交叉开关互连方式，图6.41中每个交叉点都是一套开关，除了有多路转换逻辑外，为了处理多个处理机同时访问某一存储器模块所发生的冲突，交叉开关互连方式需要有相应的仲裁部件。
在这里插入图片描述

显然，这种互连开关阵列比较复杂，当 $m, P$ 两者都为 $n$ 时，阵列所需设备量将为 $O(n^2)$ ，受集成电路工艺水平限制，一般 $n$ 不宜超过 $16$ 。随着 VLSI 技术的不断发展，这一上限正在不断提高。

此外，对于分布存储的、松耦合方式的大规模并行多处理机系统，可采用多级纵横交叉开关互连来实现众多处理机间的连接——由于交叉开关较复杂，可通过用「多个较小规模的交叉开关」“串联”和“并联”，构成多级交叉开关网络，以取代单级的大规模交叉开关。图6.42是用 $4 \times 4$ 的交叉开关构成 $16 \times 16$ 的二级交叉开关网络，使设备量减少为单级 $16 \times 16$ 的一半。这实际是用 $4 \times 4$ 的交叉开关模块构成 $4^2 ×4^2$ 的交叉开关网络，其中，指数 $2$ 为互连网络的级数。
在这里插入图片描述

在多处理机中，经常会遇到互连网络的输入端个数和输出端个数不同的情况，此时可用 $a \times b$ 的交叉开关模块，使 $a$ 中任一输入端与 $b$ 中任一输出端相连。用 $n$ 级 $a \times b$ 交叉开关模块可组成一个 $a^n ×b^n$ 的开关网络，它已被 Patel（1981年）的多处理机采用，叫做 Delta 网。因此，SIMD 的互连网络，同样也可用于多处理机间的互连——例如，多处理机用混洗交换网络互连，其通信带宽和成本介于单总线互连与交叉开关互连之间，而且比较适用于处理机数较多的多处理机中。由于多处理机的通信模式不规则，因此，能实现 $N!$ 种排列的全排列网络，同样适用于多处理机的机间互连。前面已提到，不同于 SIMD 的是，开关中带有小容量缓冲存储器。

4. 多端口存储器互连方式

这种互连方式要求每个存储器模块有多个存取端口，每个端口均有控制、转接和仲裁功能，这实际上是将纵横交叉开关互连方式，由开关阵列集中控制分散到各个端口进行分布控制。由于存储器模块的端口数不可能做得很多，因此它只适于系统中处理机数不太多的场合。

6.5.4 多处理机系统中并行性开发

由于多处理机系统中的并行性存在于不同的层次上，因此，要充分开发它的并行性就必须从算法、语言、编译、操作系统和系统结构等各方面来统筹、协调地进行。

1. 并行算法分析

当处理机数目很多时，要把问题分解成「由足够多的处理机处理的并行过程」是极其困难的。为简化讨论，以算术表达式的并行运算为例，说明并行算法的研究思路。

实际上，可把表达式看成是多个程序段相互作用的结果，而表达式中每一项，都可看成是一个程序段的运行结果。

算法必须适应具体的计算机结构——在串行机上经常采用的循环和迭代算法，往往不适合于多处理机系统，而采用直接求解法，有时反倒能揭示更多的并行性。例如，表达式 $E_1 = a + bx + cx^2 + dx^3$

利用霍纳 Horner 法可得到
$E_1 = a + x( b + x (c + x (d)))$ 这是在单处理机上执行的典型算法，共需 $3$ 个乘、 $3$ 个加运算， $6$ 级运算。但不适合于在多处理机上运行，因为它无法利用上其他的处理机。将这两式的运算过程表示为树形流程图，分别如图6.43(a)和图6.43(b)所示。
在这里插入图片描述

在图6.43中， $P$ 代表处理机的数目； $T_p$ 代表运算级数，即为树的高度； $S_p$ 为加速比，它指顺序运算的级数 $T_1$ 与 $P$ 台处理机运算的级数 $T_p$ 的比值；而 $\dfrac{S_p}{ P} = E_p$ 称为效率。可见， $S_p≥1$ 时，会使 $E_p≤1$ ，即运算的加速总是伴随着效率的下降。

既然可把运算过程表示成树形结构，那么，提高运算的并行性就是如何对树进行变换，减少运算的级数，即降低树高。树形结构可以用交换律、结合律、分配律来变换。因此，对描述运算过程的树形结构进行变换，可以作为研究并行算法的一种思路。

首先，从算术表达式的最直接形式出发，利用交换律把相同的运算集中在一起。然后，利用结合律，把参加这些运算的操作数（称原子）配对，尽可能并行运算，从而组成树高最小的子树。最后，再把这些子树结合起来。例如，表达式
$E_2 = a + b( c + def + g) + h$ 需 $7$ 级运算，如图6.44(a)所示。利用交换律和结合律，改写为
$E_2 = ( a + h) + b ( (c + g ) + def)$ 则只需 $5$ 级运算，如图6.44(b)所示。
在这里插入图片描述
利用分配律进一步降低树高，在恰当平衡各子树的级数的情况下，往往能收到较好的效果。在上式中的计算表达式中，如果改写成
$E_2 = (a + h) + (bc + bg) + bdef$ 运算过程的树形结构如图6.45所示。

2. 程序的并行性分析

任务间能否并行，除了算法外，在很大程度上还取决于程序的结构。程序中各类数据相关，是限制程序并行的重要因素。数据相关既可存在于指令之间，也可存在于程序段之间。下面从「程序段之间的数据相关」出发，分析程序的并行性问题。

假定一个程序包含 $P_1, P_2, \dots, P_i, \dots, P_j, \dots, P_n$ 等 $n$ 个程序段，其书写的顺序反映了该程序正常执行的顺序。为便于分析，设 $P_i$ 和 $P_j$ 程序段都是一条语句， $P_i$ 在 $P_j$ 之前执行，且只讨论 $P_i$ 和 $P_j$ 之间数据的直接相关关系。

在第五章中曾讲过异步流动，指令之间数据相关可能有先写后读、先读后写和写—写 $3$ 种。在多处理机上，各处理机的程序段并行必然是异步的，因此，程序段之间也必然会出现类似的 $3$ 种数据相关。为简单起见，仅以赋值语句表示程序段为例。

(1) 数据相关

如果 $P_i$ 的左部变量在 $P_j$ 的右部变量集内，且 $P_j$ 必须取出 $P_i$ 运算的结果来作为操作数，就称 $P_j$ 数据相关于 $P_i$ 。例如：

Pi : A = B + D
Pj : C = A * E

相当于流水中发生的先写后读相关。显然， $P_i$ 和 $P_j$ 不能并行执行。

(2) 数据反相关

如果 $P_j$ 的左部变量在 $P_i$ 的右部变量集内，且当 $P_i$ 未取用其变量的值之前，是不允许被 $P_j$ 所改变的，就称 $P_i$ 数据反相关于 $P_j$ 。例如：

Pi : C = A + E
Pj : A = B + D

相当于流水中发生的先读后写相关。为了保证语义上的正确性，必须等 $P_i$ 将变量 $A$ 读出以后， $P_j$ 才可向变量 $A$ 进行写操作，即必须先读后写。

对于这种相关，如果能够在硬件上保证对相关单元先读后写的次序，是可以并行的，如图6.46所示。即让每个处理机的操作结果先暂存于自己的局部存储器（或Cache存储器）中，不急于去修改原来存放于共享主存单元的内容。这样，只要控制局部存储器（或Cache存储器）向共享主存的写入同步进行即可。
图6.46 能保证读—写次序的处理机结构

(3) 数据输出相关

如果 $P_i$ 的左部变量也是 $P_j$ 的左部变量，且 $P_j$ 存入其算得的值必须在 $P_i$ 存入之后，则称 $P_j$ 数据输出相关于 $P_i$ 。例如：

Pi : A = B + D
Pj : A = C + E

按原执行顺序 $A_新$ 应为 $C + E$ 。可见，只要同步能保证 $P_i$ 先写入之后 $P_j$ 再写入，这两个程序段可以并行。

(4) 交换数据相关

除了上述 $3$ 种相关外，如果两个程序段的输入变量互为输出变量，同时具有先写后读和先读后写两种相关，以交换数据为目的，则两者必须并行执行，既不能顺序串行，也不能交换串行。例如，两语句的左、右变量互相交换：

Pi : A = B
Pj : B = A

必须并行执行，且需要保证读写完全同步。当然，如果在图6.46的多处理机上运行这样的程序段，就能自动保证读/写次序，降低对同步的要求。

(5) 总结和伯恩斯坦准则

综上所述，两个程序段之间若有先写后读的数据相关，不能并行执行；若有先读后写的数据反相关，可以并行执行，但必须保证其写入共享主存时的先读后写次序；若有写—写的数据输出相关，可以并行执行，但同样须保证其写入的先后次序；若同时有先写后读和先读后写两种相关，以交换数据为目的时，必须并行执行，且读写要完全同步。

下面介绍由伯恩斯坦 Bernstein 提出的一种自动判别数据相关的准则。每个程序段在执行过程中，通常要使用输入和输出这两个分离的变量集。若用 $I_i$ 表示 $P_i$ 程序段中操作所要读取的存储单元集，用 $O_i$ 表示要写入的存储单元集，则 $P_1$ 和 $P_2$ 两个程序段能并行执行的伯恩斯坦准则为：

$I_1 ∩ O_2 = \varnothing$ ，即 $P_1$ 的输入变量集与 $P_2$ 的输出变量集不相交；
$I_2 ∩ O_1 = \varnothing$ ，即 $P_2$ 的输入变量集与 $P_1$ 的输出变量集不相交；
$O_1 ∩ O_2 = \varnothing$ ，即 $P_1$ 和 $P_2$ 的输出变量集不相交。

例如，若有三个程序段 $P_1, P_2 , P_3$ 分别求三个矩阵算术表达式：
$\begin{aligned} &P_1 : X = ( A + B) × (A - B) \\ &P_2 : Y = (C - 1) × (C + D) - 1 \\ &P_3 : Z = X + Y \end{aligned}$ 其中， $A, B, C, D, X, Y$ 均为 $N \times N$ 的矩阵，它们的输入、输出变量集分别为：
$\begin{aligned} &I_1 = \{A, B\} ,\ I_2 = \{C, D\},\ I_3 = \{X, Y\}, \\ &O_1 = \{X\},\ O_2 = \{Y\},\ O_3 = \{Z\} \end{aligned}$ 由于 $I_1 ∩ O_2 = \varnothing,\ I_2 ∩ O_1 = \varnothing,\ O_1 ∩ O_2 = \varnothing$ ，故 $P_1$ 和 $P_2$ 两个程序段可以并行执行；由于 $I_3 ∩ O_1 ≠ \varnothing$ 和 $I_3 ∩ O_2 ≠ \varnothing$ ，故 $P_3$ 程序段必须在 $P_1$ 和 $P_2$ 程序段执行完毕，方可开始执行。

3. 并行程序设计语言

并行算法需要用并行程序来实现。为了加强程序并行性的识别能力，有必要在程序语言中，增加能「明确表示并发进程的成分」，这就要使用并行程序设计语言。

并行程序设计语言的产生有两种方法：一是，可以在普通顺序型语言上加以扩充，增加能明确表示并行进程的成分，但每一种经扩充的语言仅能支持一种类型的并行性；二是，可以通过设计全新的并行程序设计语言，支持并行处理。一般采用前一种方法比较现实。

并行程序设计语言的基本要求是：能使程序员在其程序中灵活方便地表示出各类并行性，能在各种并行/向量计算机系统中高效地实现。

(1) 使用 `FORK-JOIN` 语句来表示并发性

FORK_JOIN 语句在不同机器上有不同的表示形式。现以 M. E. Conway 提出的形式为例说明。

FORK 语句的形式为 FORK m ，其中 m 为新进程开始的标号。执行 FORK m 语句时，派生出标号从 m 开始的新进程，当前的进程仍继续执行。具体功能包括：
① 准备好这个新进程启动和执行所必需的信息；
② 如果现有空闲的处理机，则将其分配给已派生的新进程，否则，让它们排队等待；
③ 继续在原处理机上执行 FORK 语句以后的原进程。

与 FORK 语句相配合、作为每个并发进程的终端（终结？）语句 JOIN 的形式为 JOIN n ，其中 n 为已派生出的并发进程个数。JOIN 语句附有一个计数器（记录终结了多少个派生出的并发进程），其初始值为 $0$ 。每当执行一个 JOIN n 语句时，计数器的值加 $1$ ，并与 n 比较。

若比较相等，表明这是执行的第 n 个（最后一个）并发进程经过 JOIN n 语句，于是允许该进程通过 JOIN 语句，将计数器清 $0$ （所有派生的并发进程已经终止），并在其处理机上继续执行后续语句。（？）
若比较，计数器的值仍小于 n ，表明此进程不是并发进程中的最后一个，可让「现在执行 JOIN 语句的这个进程」先结束，把它所占用的处理机释放出来，分配给正在排队等待的其他进程或让该处理机空闲。

下面仍以算术表达式 $Z = E + A \times B \times C / D + E$ 的计算为例，经并行编译得到如下程序：

S1 : G = A × B
S2 : H = C / D
S3 : I = G × H
S4 : J = E + F
S5 : Z = I + J

如果不加并行控制语句，这个程序仍然只是一个普通的串行程序，发挥不出多处理机的作用。图6.47示出了各语句间的数据相关情况。它表明 $S_1$ 和 $S_2$ 可以同时开始执行，但要等到 $S_1$ 和 $S_2$ 都完成之后，才能开始执行 $S_3$ ，并可并行地开始执行 $S_4$ ，而只有 $S_4$ 和 $S_3$ 汇合才能执行 $S_5$ 。
在这里插入图片描述

利用 FORK_JOIN 语句实现这种派生和汇合关系，将程序改写为：

	FORK 20		; 派生出一个新的进程 S2
10	G = A × B   ; 当前的处理机继续执行 S1
	JOIN 2		; 结束进程 S1, 并比较计数器值是否等于 2

	GOTO 30	
20  H = C / D 	; 执行进程 S2
	JOIN 2

30  FORK 40     ; 派生新进程 S4
	I = G × H	; 执行进程 S3
	JOIN 2

	GOTO 50
40  J = E + F   ; 执行进程 S4
	JOIN 2
	
50  Z = I + J	; 执行进程 S5

执行这个程序可用两台处理机。假定最初的程序是在处理机 $1$ 上运行的，遇到 FORK 20 语句时就分出一个处理机（假定是 $2$ ）去执行 $S_2$ ，而处理机 $1$ 接着执行下面的 $S_1$ 。如果 $S_1$ 执行时间较短，当它结束时遇到 JOIN 2 语句， $S_2$ 尚在执行，处理机 $1$ 从 $S_1$ 释放，因无其他任务处于空闲。随后当 $S_2$ 结束时，由于已与 $S_1$ 汇合，便可以通过 JOIN 语句，由处理机 $2$ 继续执行后续的 FORK 40 语句。这条语句又派生出 $S_4$ ，分配给空闲的处理机 $1$ ，而处理机 $2$ 接着执行 $S_3$ 。同样，等 $S_4$ 和 $S_3$ 都先后结束，才满足 JOIN 语句的汇合条件，经 GOTO 50 进入 $S_5$ 。其执行过程见图6.48。
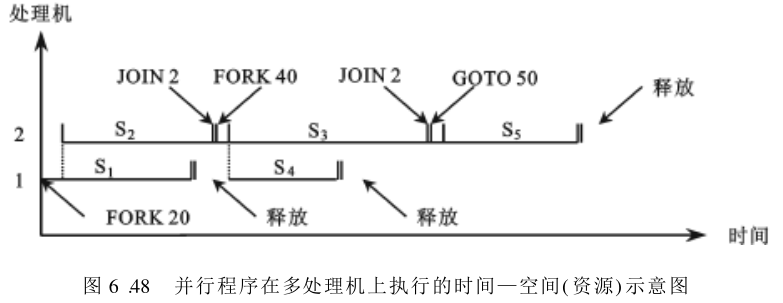
图6.48 并行程序在多处理机上执行的时间—空间（资源）示意图

(2) 使用块结构语言来表示并行性

块结构语言与 FORK_JOIN 语句在概念上是等价的，但使用更为方便。它用 cobegin-coend（或 parbegin-parend）将所有可并行执行的语句或进程前后括起来，以显式表明它们可并行执行。例如：

begin
	S0;
	cobegin S1; S2; ...; coend
	Sn + 1;
end

其中， $S_1, S_2, \dots, S_n$ 为可并行执行的语句。而语句 $S_{n + 1}$ 则必须在 $S_1, S_2, \dots, S_n$ 全部执行完后，方可开始执行。每一组的并行语句只有一个入口和出口，因此符合结构化程序设计要求。此外，并行语句中所定义的各个进程互相独立，具有不相交性，即每个语句所能修改的变量，只属于该进程专有的局部变量。虽然不相交进程间可使用共享变量，但只能读，不可修改。并行语句还可任意嵌套使用。图6.49中示出了嵌套执行情况。例如：
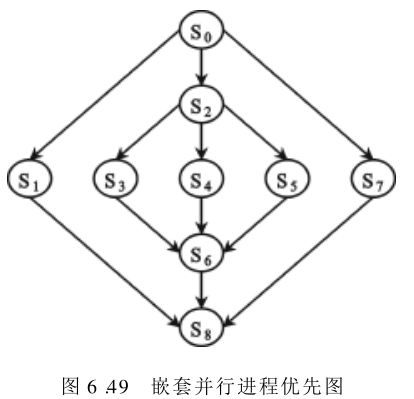
图6.49 嵌套并行进程优先图

begin
	S0;
	cobegin
		S1;
		begin
			S2;
			cobegin S3; S4; S5; coend
			S6;
		end
		S7;
	coend
	S8;
end

在循环程序中通常可找到可并行执行的语句，此时可用并行循环 parfor 语句来表示这种并行性。例如，若要进行矩阵运算 $C = A \times B$ ，其中 $A$ 为一个 $n \times n$ 的矩阵，而 $B$ 和 $C$ 则均为 $n \times 1$ 的列向量。下面列出使用 parfor 语句的求解算法，它能派生出 $p$ 个独立进程。假定 $p$ 能整除 $n$ ，则有 $\dfrac{n}{ p}$ ：

parfor i = 1 until p do
	begin
		for j = (i - 1)s + 1 until s × i do
			begin
				c(j) = 0;
				for k = 1 until n do
					c(j) = c(j) + A(j, k) × B(k);
			end
	end

每个被派生的进程，根据不同的 $i$ 值计算最外层 begin - end 之间的语句。为方便说明起见，不妨假设 $n = 12, p = 4, s = 3$ ，则执行 parfor 语句将派生出四个独立进程，分别对应于 $i = 1, 2, 3, 4$ 。此后，这四个进程可并行执行最外层 begin-end 之间的语句。

对 $i = 1$ 的独立进程，将得到最终计算结果： $C (1), C (2), C (3)$ 。对 $i = 2$ 的独立进程，将得到最终计算结果：$C( 4) , $C (5), C (6)$ 。而对 $i = 3$ 和 $i = 4$ 的两个独立进程，则分别得到最终计算结果： $C (7) ～ C (9)$ 和 $C (10) ～ C (12)$ 。

6.5.5 多处理机操作系统

1. 多处理机操作系统的特点

从概念上讲，多处理机操作系统与单处理机的多道程序操作系统无多大差别。但当多台处理机同时工作时，操作系统的复杂性就增加了。当要求其支持异步任务并发执行时，复杂性问题就显得更加突出了。

多处理机操作系统除了要完成通常单机操作系统的资源分配和管理、存储管理和保护、死锁防止、异常进程终止或例外处理等功能外，还必须具有如下的特点和功能：

支持多个任务的并行执行，为此需要研究任务的分解和分派、以及处理机间负载平衡问题。
支持处理机间同步和通信管理。
提供系统结构重构能力，以支持系统降级使用。
自动支持硬件并行性和程序并行性的开发。

2. 多处理机操作系统

多处理机操作系统有主从型 Master-Slave Supervisor 、各自独立型 Separate Supervisor 及浮动型 Floating Supervisor 三类。

(1) 主从型操作系统

主从型操作系统中的管理程序只在一台指定的处理机（主处理机）上运行。该主处理机可以是「专门的、执行管理功能的控制处理机」，也可以是「与其他从处理机相同的通用机」，除执行管理功能外，也能做其他方面的应用。

由于主处理机负责管理系统中所有其他处理机（从处理机）的状态及其工作的分配，只把从处理机看成是一个可调度的资源，实现对整个系统的集中控制，因此，也称为集中控制或专门控制方式。从处理机通过访管指令或自陷软中断，请求主处理机服务。

这种主从型控制方式的系统硬件结构比较简单。整个管理程序只在一台处理机上运行，除非某些需递归调用或多重调用的公用程序，一般都不必是可再入的；只有一个处理机访问执行表（？），不存在「系统管理控制表格」的访问冲突和阻塞，简化了管理控制的实现。所有这些，均使这种操作系统能最大限度地利用「已有的单处理机多道程序分时操作系统」的成果，只需要对它稍加扩充即可。因此，实现起来简单、经济、方便，是目前大多数多处理机操作系统所采用的方式。

然而，主从型也有许多不足之处——对主处理机的可靠性要求很高，一旦发生故障，很容易使整个系统瘫痪，这时必须要由操作员干预才行。如果主处理机不是设计成专用的，操作员可用其他处理机作为新的主处理机，来重新启动系统。整个系统显得不够灵活，同时要求主处理机必须能快速执行其管理功能，提前等待请求，以便及时为从处理机分配任务，否则将使从处理机因长时间空闲、而显著降低系统的效率。

即使主处理机是专门的控制处理机，如果负荷过重，也会影响整个系统的性能。特别是当大部分任务都很短时，由于频繁地要求主处理机完成大量的管理性操作，系统效率将会显著降低。

主从型操作系统适合于工作负荷固定、且从处理机能力明显低于主处理机，或由功能相差很大的处理机组成的异构型多处理机。

(2) 各自独立型操作系统

与主从型操作系统不同，各自独立型操作系统将控制功能分散给多台处理机，共同完成对整个系统的控制工作。每台处理机都有一个独立的管理程序（操作系统的内核）在运行，即每台处理机都有一个内核的副本，按自身的需要及分配给它的程序需要，执行各种管理功能。

由于多台处理机执行管理程序，要求管理程序必须是可再入的，或对每台处理机提供专门的管理程序副本。这种方式的优点是，很适应分布处理的模块化结构特点，减少对大型控制专用处理机的需求；某个处理机发生故障，不会引起整个系统瘫痪，有较高的可靠性；每台处理机都有其专用控制表格，使访问系统表格的冲突较少，也不会有许多公用的执行表；同时将控制进程和用户进程一起进行调度（？），能取得较高的系统效率。

然而，这种方式实现复杂。尽管每台处理机有自己的专用控制表格，但仍有一些共享表格会增加共享表格的访问冲突，导致进程调度的复杂性和开销加大。某台处理机一旦发生故障，要想恢复和重新执行未完成的工作较困难。每台处理机都有自己专用的输入输出设备和文件，使整个系统的输入输出结构变换需要操作员干预。各台处理机需要局部存储器存放管理程序副本，降低了存储器的利用率。各处理机负荷的平衡比较困难。

各自独立型操作系统适合于松耦合多处理机。

(3) 浮动型操作系统

浮动型操作系统是界于主从型操作系统和各自独立型操作系统之间的一种折衷方式，其管理程序可以在处理机之间浮动。在一段较长的时间里指定某一台处理机为控制处理机，但是具体指定哪一台处理机、以及担任多长时间控制，都是不固定的。

主控制程序可以从一台处理机转移到另一台处理机，其他处理机中可以同时有多台处理机执行同一个管理服务子程序，因此，多数管理程序必须是可再入的。由于同一时间里可以有多台处理机处于管态，有可能发生访问表格和数据集的冲突，一般采用互斥访问方法解决。服务请求冲突可通过静态分配或动态控制高优先级方法解决。

这种系统可以使各类资源做到较好的负荷平衡。一些像 I/O 中断等非专门的操作，可交由在某段时间最闲的处理机去执行。它在硬件结构和可靠性上具有分布控制的优点，而在操作系统的复杂性和经济性上，则接近于主从型。如果操作系统设计得好，将不受处理机机数的多少所影响，因而具有很高的灵活性。然而，这种操作系统的设计是最困难的。

这种方式的操作系统适用于紧耦合多处理机，特别是由「共享主存和 I/O 子系统的多个相同处理机」组成的同构型多处理机。

6.5.6 多处理机的调度策略

在多处理机系统中，能否对资源进行有效分配是决定多处理机系统性能的关键，特别是当系统中处理机的数目很多的时候。

在多处理机系统中，资源分配要解决的主要问题是：一个进程应分配到哪个处理机上运行：

同构型多处理机系统的调度策略是，将各种资源包括处理机、主存、I/O 通道等，存放在一个公共的资源池中，为所有进程共享，以求提高资源利用率、尽量使各处理机的负载平衡。
对异构型多处理机系统而言，由于每个处理机所需完成的功能不同，因此调度工作主要是按处理机的功能如控制、数据处理、输入/输出等，分配任务，使各个处理机各司其职。

衡量多处理机调度性能好坏的主要参数通常有：完成所有任务所需的最少时间；完成所有任务所需的最少处理机数；最小平均流时间，即执行每个任务所需的平均时间；处理机的最大利用率或处理机的最小空闲时间。

图6.50示出了一个任务调度时空图，表示在三个处理机 $P_1, P_2, P_3$ 上执行五个任务 $T_1 ～T_5$ 的时空图。各个任务的执行时间分别为 $7,\ 6.5,\ 2,\ 2,\ 2$ 。完成所有任务所需总的时间为 $19.5$ 。平均流时间为 $19.5 / 5 = 3.9$ 。 $P_1, P_2, P_3$ 的利用率分别为 $0.93,\ 1.00,\ 0.86$ 。它们的空闲时间分别为 $0.5,\ 0.0,\ 1.0$ 。
在这里插入图片描述
多处理机调度实质上就是要寻找一种调度算法，其调度目标是使用最少量的处理机在最短时间内完成全部任务。调度算法通常要依据一个模型进行，目前主要流行的调度模型有两种：静态的确定性模型和动态的随机性模型。下面以静态的确定性调度模型为例说明。

这种调度模型要求，在求解问题前就已知「执行每个任务所需的时间」以及「系统中各任务间的关系」。这种调度算法的设计较简单，但如果事先不能准确估计每个任务的执行时间及任务间关系，该调度算法的效率就不高。在确定性调度模型中，可以根据不同的调度环境采用不同的算法。为简单起见，我们只讨论由「一组相同的处理机」和「具有确定优先关系的一组任务」所组成的调度环境，并采用可抢占调度——所谓抢占调度是指一个任务在被完成之前，允许被中断，此后又可恢复执行的调度。只要这种抢占不过于频繁，那么它的效率就优于非抢占调度。

通常把一个任务集合称为任务系统，可用一个优先图来表示。图中节点表示「具有独立操作且需要与其他节点联系的任务」。节点集合表示了任务集合 $\{ T_1, \dots, T_n \}$ ，节点间的有向边表示了任务间存在的偏序或优先关系。此外，每个节点还有称为权重的另一个属性，它指明由该节点所表示的任务，在处理机上运行时所需的时间。任务调度必须符合以下的原则：

遵循偏序关系。
任何时候只能将一台处理机分配给一个任务。

假定一个任务图包含节点权重为 $t_1, t_2, \dots, t_n$ 的 $n$ 个独立任务和 $p$ 台处理机，则最优调度所需的最小时间为：
$\max \{ \max_{1≤ i≤ n } \{t_i \}, \ \dfrac { \sum^n_{ i = 1} t_i } { p}\}$ 即最小执行时间不可能小于最长任务的执行时间（括号中第一项）或处理机的平均执行时间（括号中的第二项）。

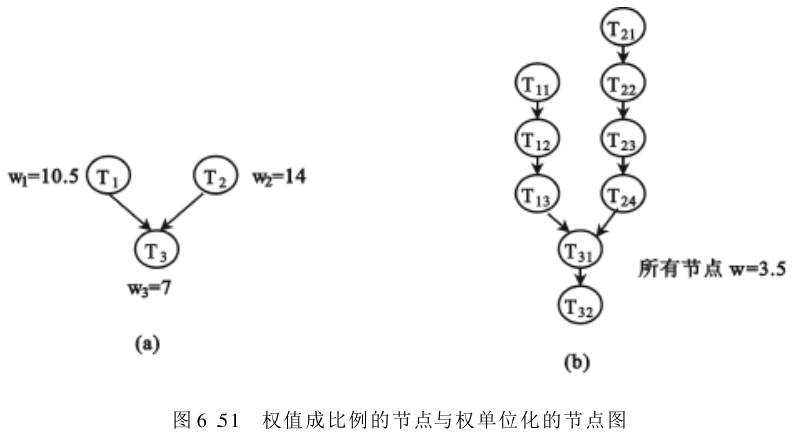
为了实现优化调度，首先，要把任务图 $G$ 中的所有节点的权值，单位化成「具有相同权值的节点」组成的图 $G_W$ ，如图6.51(a)所示。图6.51(b)中的图 $G_W$ ，权值已单位化成 $W = 3.5$ 。
在这里插入图片描述然后，将图 $G_W$ 中的全部节点分解成若干个不相交的子集系列，使每个子集中的节点彼此独立，这样「处于同一子集或同一级中的所有节点」便可同时执行。对于如图6.52(a)中的图 $G_W$ ，它的最佳子集序列应为 ${ T_1 \},\ \{ T_2, T_3 \},\ \{ T_5, T_6, T_7 \},\ \{ T_4, T_8 \},\ \{T_9, T_{10} \},\ \{ T_{11} \}$ 。图6.52(a)的各级是这样划分的，结束节点（图中为 $T_{11}$ ）为第一级，在此之前的单位时间内，可以执行的那些节点为第二级（图中为 $T_9$ 和 $T_{10}$ ），依此类推直至图中的入口节点为止。
图 6.52 按独立子集顺序进行抢占的优先调度
当处理机的数目为 $2$ 时，若每一级中的任务数为偶数，则该级中所有任务都能充分地利用两台处理机，在最短时间内完成所有的任务。若任务数为奇数时，则最后三个任务的完成时间将大于或等于 $1.5$ 单位时间。如图6.52(b)中所示那样， $T_5, T_6, T_7$ 三个任务只需用 $1.5$ 单位时间便可完成， $T_6$ 任务在 $P_2$ 中未被完成前，为 $T_7$ 任务中断抢先， $T_6$ 然后被迁移到 $P_1$ 中去完成。

整个的任务调度是如下进行的：开始时因只有 $T_1$ 任务无前趋，因此将它调度到 $P_1$ 处理机上去完成，单位时间后 $T_1$ 被完成，此时 $T_2, T_3 , T_4$ 三个任务均无前趋，可并行执行，但因只有两台处理机，所以只能选其中两个任务： $T_2, T_3$ （因为这两个任务处在同一子集）。在此之后， $T_5, T_6 , T_7$ 以及原来的 $T_4$ 均无前趋，由于前三个任务处在同一子集，因此优先调度执行。