Adversarial Robustness

Motivation$\text{: a limitation of the (supervised) ML framework}$

The current way of training and inference is to train the ML model on some randomly drawn samples and test on some other independently drawn samples. A crucial assumption behind this is that the distribution that we use to train the ML model is exactly the distribution that the model will encounter. In reality, this is not the case as there are various forms of covariate shifts. Due to lack of this assumption, ML (particularly DL) predictions are brittle despite (mostly) accurate.

ML and adversarially robust ML

learning objective

In fact, lack of adversarial robustness is not at odds with what we currently want our ML models to achieve.

• standard generalization (average case performance): ${\mathbb{E}}_{(x,y)\sim D}[loss(\theta ,x,y)]$
• adversarial robust generalization (worst-case notion, measure zero event): ${\mathbb{E}}_{(x,y)\sim D}[{\max }_{\delta \in \Delta }loss(\theta ,x+\delta ,y)]$

generalization of standard and robust deep networks

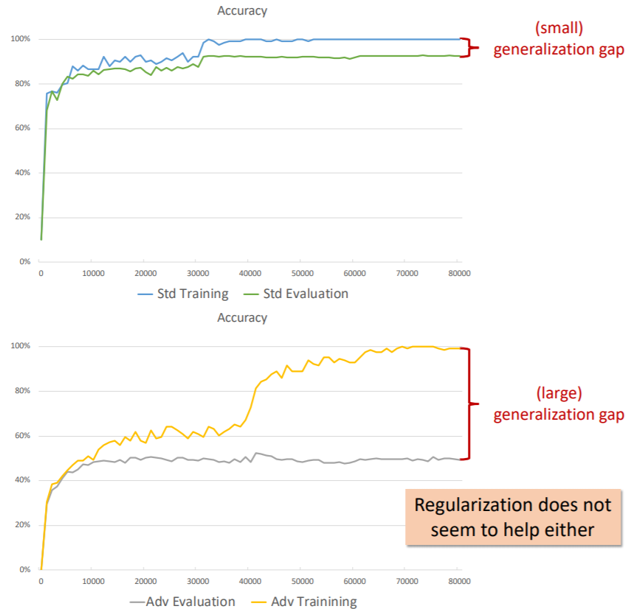
Not only does the optimization problem become more challenging and the model become larger(training), adversarial robustness has a significantly larger sample complexity, thus its generalization requires more data (test).

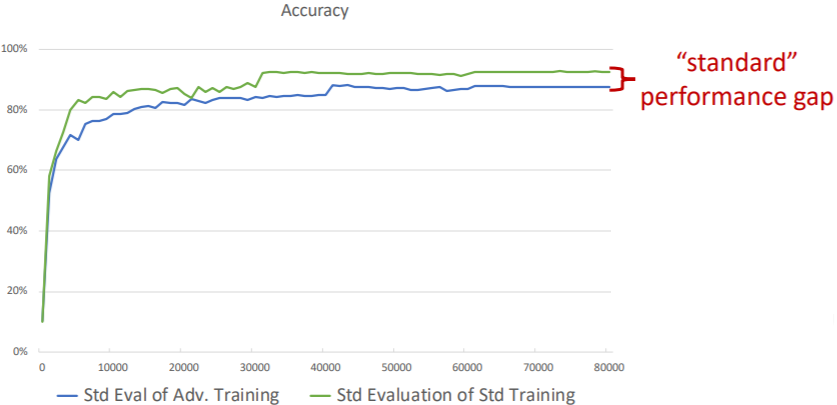
No ‘free lunch’: can exist a trade-off between accuracy and robustness. Intuitively,

• in standard training, all correlation among features is a good correlation (so-called non-robust features in [3]);
• if we want robustness, must avoid weakly correlated features.

interpretability

Adversarial Examples and Verification (inner minimization)

$$\underset{\theta }{\min }\sum _{(x,y)\sim S}\underset{\text{Part I. create AEs or verify it does not exist}}{\underbrace{\underset{\delta \in \Delta }{\max }L(\theta ,x+\delta ,y)}}$$

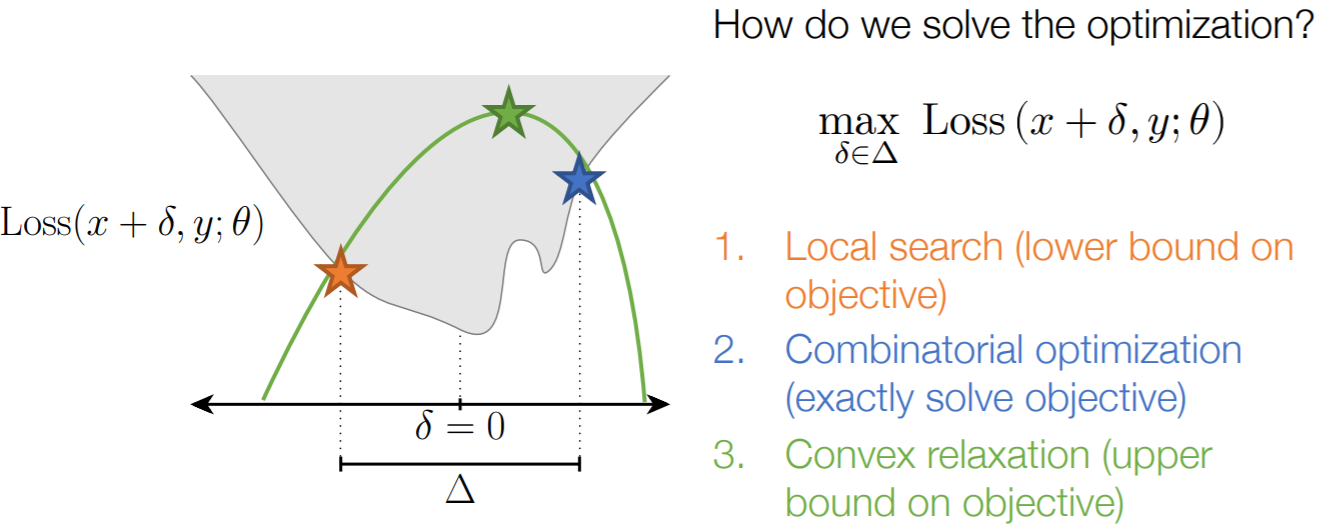
In the linear case with a norm ball perturbation region, the maximization has exact solution based on dual norm; a simple instance of robust optimization. That is,
max ⁡ δ L ( θ T ( x + δ ) ⋅ y ) = L ( min ⁡ δ θ T ( x + δ ) ⋅ y ) = L ( θ T x ⋅ y − ∥ θ ∥ ∗ ) \begin{aligned} \max_\delta L(\theta^T (x + \delta) \cdot y) &=L(\min_\delta \theta^T (x + \delta) \cdot y)\\ &=L(\theta^T x \cdot y - \| \theta \|_\ast) \end{aligned} δmax​L(θT(x+δ)⋅y)</