本着不在NOIP前碰多项式的原则,我现在开始学FFT。
多项式的表示
系数表示: f ( x ) = ∑ i = 0 n a i x i f(x)=\sum_{i=0}^na_ix^i f(x)=∑i=0naixi,则 a a a是 f f f的系数表示。
点值表示:一个长为 n + 1 n+1 n+1的数组,其中元素为 ( d i , f ( d i ) ) (d_i,f(d_i)) (di,f(di)), d d d是元素互不相同的数组。
可以使用DFT和IDFT在 O ( n log n ) O(n\log n) O(nlogn)复杂度内将系数表示与点值表示互相转换。
k k k次单位根
k k k次单位根是其 k k k次幂为 1 1 1的一些复数,共有 k k k个,分别为 e 2 π i j k ( j ∈ [ 0 , k − 1 ] ) e^\frac{2\pi i j}{k}(j\in [0,k-1]) ek2πij(j∈[0,k−1])。记 ω k = e 2 π i k \omega_k=e^\frac{2\pi i}{k} ωk=ek2πi,则 k k k次单位根可分别表示为 w k i ( i ∈ [ 0 , k − 1 ] ) w_k^i(i\in[0,k-1]) wki(i∈[0,k−1])。
在复平面上, k k k次单位根是单位圆上均匀分布的 k k k个点,其中第 0 0 0个在 ( 1 , 0 ) (1,0) (1,0),接下来的依次按逆时针绕一圈。容易想到单位根有以下性质:
- ω k i = ω k 2 i 2 \omega_k^i=\omega_{\frac{k}{2}}^\frac{i}{2} ωki=ω2k2i
- ω k i = − ω k i + k 2 \omega_k^i=-\omega_k^{i+\frac{k}{2}} ωki=−ωki+2k
- ω k i = cos i k 2 π + i ⋅ sin i k 2 π \omega_k^i=\cos\frac{i}{k}2\pi+i\cdot\sin\frac{i}{k}2\pi ωki=coski2π+i⋅sinki2π
DFT
用于将系数表示转化为点值表示。
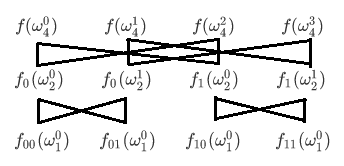
先将 f ( x ) f(x) f(x)的阶向上扩充为 2 k − 1 2^k-1 2k−1(多余部分的 a i = 0 a_i=0 ai=0)。设此时 f ( x ) f(x) f(x)的阶为 n − 1 n-1 n−1,考虑将 n n n次单位根作为 d d d数组,即 d i = ω n i d_i=\omega_n^i di=ωni。
设 f 0 ( x ) = a 0 x 0 + a 2 x 1 + ⋯ + a n − 1 x n 2 f_0(x)=a_0x^0+a_2x^1+\cdots+a_{n-1}x^{\frac{n}{2}} f0(x)=a0x0+a2x1+⋯+an−1x2n, f 1 ( x ) = a 1 x 0 + a 3 x 1 + ⋯ + a n − 2 x n 2 f_1(x)=a_1x^0+a_3x^1+\cdots+a_{n-2}x^{\frac{n}{2}} f1(x)=a1x0+a3x1+⋯+an−2x2n。显然 f ( x ) = f 0 ( x 2 ) + x f 1 ( x 2 ) f(x)=f_0(x^2)+xf_1(x^2) f(x)=f0(x2)+xf1(x2)。
于是 f ( ω n i ) = f 0 ( ω n 2 i ) + ω n i f 1 ( ω n 2 i ) = f 0 ( ω n 2 i ) + ω n i f 1 ( ω n 2 i ) f(\omega_n^i)=f_0(\omega_n^{2i})+\omega_n^if_1(\omega_n^{2i})=f_0(\omega_\frac{n}{2}^i)+\omega_n^if_1(\omega_\frac{n}{2}^i) f(ωni)=f0(ωn2i)+ωnif1(ωn2i)=f0(ω2ni)+ωnif1(ω2ni)。
同理可以得到 f ( ω n i + n 2 ) = f ( − ω n i ) = f 0 ( ω n 2 i ) − ω n i f 1 ( ω n 2 i ) f(\omega_n^{i+\frac{n}{2}})=f(-\omega_n^i)=f_0(\omega_\frac{n}{2}^i)-\omega_n^if_1(\omega_\frac{n}{2}^i) f(ωni+2n)=f(−ωni)=f0(ω2ni)−ωnif1(ω2ni)。
看到没? f 0 f_0 f0和 f 1 f_1 f1中带入的值是一样的,因此我们可以分治递归解决问题。复杂度为 O ( n log n ) O(n\log n) O(nlogn)。
IDFT
用于将点值表示转化为系数表示。该过程等价于用 ω n i + n 2 \omega_n^{i+\frac{n}{2}} ωni+2n替换 ω n i \omega_n^i ωni做DFT,再将结果除以 n n n。复杂度为 O ( n log n ) O(n\log n) O(nlogn)。
DFT和IDFT统称为FFT(Fa Fa Tower)。实际实现中,应用雷德(Rader)算法来优化常数,用迭代模拟递归的过程。即先枚举层,再枚举每个“计算块”。数组下标需要进行变换成如
{
0
,
4
,
2
,
6
,
1
,
5
,
3
,
7
}
\{0,4,2,6,1,5,3,7\}
{0,4,2,6,1,5,3,7}这样。
const double pi = 3.14159265358979323846264338327950288419716939937510582097494459230781640628620899;
struct complex {
double r, v;
complex() {}
complex(double rr, double vv) {r = rr; v = vv;}
};
inline complex operator + (complex a, complex b) {
return complex(a.r+b.r, a.v+b.v);
}
inline complex operator - (complex a, complex b) {
return complex(a.r-b.r, a.v-b.v);
}
inline complex operator - (complex x) {
return complex(-x.r, -x.v);
}
inline complex operator * (complex a, complex b) {
return complex(a.r*b.r-a.v*b.v, a.r*b.v+a.v*b.r);
}
const int maxn = 1<<17;
void fft(complex a[], int n, bool typ) {
for(int i = 1, j = n>>1; i < n; i++) {
if(i < j) swap(a[i], a[j]);
for(int k = n>>1; (j^=k) < k; k >>= 1);
}
for(int i = 1; i < n; i <<= 1) for(int j = 0; j < n; j += i<<1) {
complex w = complex(1, 0), wn = complex(cos(pi/(double)i), (typ?1:-1)*sin(pi/(double)i));
for(int k = 0; k < i; k++) {
complex u = a[j+k], v = w * a[j+i+k];
a[j+k] = u + v;
a[j+i+k] = u - v;
w = w * wn;
}
}
if(!typ) for(int i = 0; i < n; i++) a[i].r /= n;
}
complex tmp[maxn<<1];
void Mul(complex a[], int an, complex b[], int bn) {
if(an <= 48 || bn <= 48) {
for(int i = 0; i < an+bn-1; i++) tmp[i] = complex(0, 0);
for(int i = 0; i < an; i++) for(int j = 0; j < bn; j++) tmp[i+j] = tmp[i+j] + a[i] * b[j];
for(int i = 0; i < an+bn-1; i++) a[i] = tmp[i];
return;
}
int n = 1;
while(n < an+bn-1) n <<= 1;
fft(a, n, 1); fft(b, n, 1);
for(int i = 0; i < n; i++) a[i] = a[i] * b[i];
fft(a, n, 0);
}
卷积
即多项式乘法。多项式 f f f与 g g g的卷积为 h h h,设 f f f的阶为 n n n, g g g的阶为 m m m,则 h h h的阶为 n + m n+m n+m。设 f f f、 g g g的系数数组分别为 a a a、 b b b,则 h h h的系数数组 c c c满足 c i = ∑ j = 0 i a j b i − j c_i=\sum_{j=0}^ia_jb_{i-j} ci=∑j=0iajbi−j。也可理解为 a i a_i ai和 b j b_j bj对 c i + j c_{i+j} ci+j有 + a i b j +a_ib_j +aibj的贡献。
可以看到朴素的卷积算法复杂度为 O ( n m ) O(nm) O(nm)。但若先将 f f f与 g g g转化为点值表示后再相乘,则乘法的复杂度直接降为 O ( n + m ) O(n+m) O(n+m)。因此卷积的复杂度等于FFT的复杂度,即 O ( n log n ) O(n\log n) O(nlogn)。
NTT
用于解决模意义下的系数表示与点值表示相转化。设模数为 P P P。
由于 ω n n ≡ g P − 1 ≡ 1 ( m o d P ) \omega_n^n\equiv g^{P-1}\equiv1\pmod P ωnn≡gP−1≡1(modP),因此 ω n i ≡ g i ⋅ ( P − 1 ) n \omega_n^i\equiv g^\frac{i\cdot(P-1)}{n} ωni≡gni⋅(P−1)。将原来的单位根换为原根即可。
const int maxn = 1<<17;
int w[2][1<<19];
void nttinit() {
for(int i = 0; i <= 18; i++) {
w[1][1<<i] = w[0][1<<i] = 1;
int wn = qpow(gmd, md-1>>i+1), invwn = inv(wn);
for(int j = (1<<i)+1; j < 1<<i+1; j++) {
w[1][j] = mul(w[1][j-1], wn);
w[0][j] = mul(w[0][j-1], invwn);
}
}
}
void ntt(int a[], int n, bool typ) {
for(int i = 1, j = n>>1; i < n; i++) {
if(i < j) swap(a[i], a[j]);
for(int k = n>>1; (j^=k) < k; k >>= 1);
}
for(int i = 1; i < n; i <<= 1) for(int j = 0; j < n; j += i<<1) for(int k = 0; k < i; k++) {
int u = a[j+k], v = mul(w[typ][i+k], a[j+i+k]);
a[j+k] = add(u, v);
a[j+i+k] = sub(u, v);
}
if(!typ) {
int invn = inv(n);
for(int i = 0; i < n; i++) f[i] = mul(f[i], invn);
}
}
int tmp[maxn<<1];
void Mul(int a[], int an, int b[], int bn) {
if(an <= 48 || bn <= 48) {
memset(tmp, 0, (an+bn-1)*sizeof(int));
for(int i = 0; i < an; i++) for(int j = 0; j < bn; j++) Add(tmp[i+j], mul(a[i], b[j]));
memcpy(a, tmp, (an+bn-1)*sizeof(int));
return;
}
int n = 1;
while(n < an+bn-1) n <<= 1;
ntt(a, n, 1); ntt(b, n, 1);
for(int i = 0; i < n; i++) a[i] = mul(a[i], b[i]);
ntt(a, n, 0);
}
采用vector的版本:
typedef vector<int> pol;
void ntt(pol& f, int typ) {
int n = f.size();
for(int i = 1, j = n>>1; i < n; i++) {
if(i < j) swap(f[i], f[j]);
for(int k = n>>1; (j ^= k) < k; k >>= 1);
}
for(int i = 1; i < n; i <<= 1) for(int j = 0; j < n; j += i<<1) for(int k = 0; k < i; k++) {
int u = f[j+k], v = mul(w[typ][i+k], f[j+i+k]);
f[j+k] = add(u, v);
f[j+i+k] = sub(u, v);
}
if(!typ) {
int invn = inv(n);
for(int i = 0; i < n; i++) f[i] = mul(f[i], invn);
}
}
FWT
用于求位运算(集合)卷积。同样我们先对原来的两个数组进行处理,再 O ( n ) O(n) O(n)相乘,再逆变换回去。
或FWT
考虑对数组的一种变换 F W T ( A ) = B FWT(A)=B FWT(A)=B,满足 B [ i ] = ∑ i ∣ j = i A [ j ] B[i]=\sum_{i|j=i}A[j] B[i]=∑i∣j=iA[j]。这个可以通过分治在 O ( n log n ) O(n\log n) O(nlogn)时间内做到。
将数组的长度向上扩充到 2 k 2^k 2k,设其为 n n n。假设当前我们在处理区间 [ l , r ] [l,r] [l,r],并且已经计算完了 [ l , m i d ] [l,mid] [l,mid]与 [ m i d + 1 , r ] [mid+1,r] [mid+1,r]自己区间内部的影响,考虑合并。我们发现 l + i l+i l+i这个数及其二进制子集一定是 m i d + i + 1 mid+i+1 mid+i+1这个数的二进制子集,因此对于所有 i ∈ [ 0 , r − l + 1 2 ] i\in[0,\frac{r-l+1}{2}] i∈[0,2r−l+1]将 l + i l+i l+i的答案累加到 m i d + i + 1 mid+i+1 mid+i+1上即可。即 F W T ( L : R ) = F W T ( L ) : ( F W T ( L ) + F W T ( R ) ) FWT(L:R)=FWT(L):(FWT(L)+FWT(R)) FWT(L:R)=FWT(L):(FWT(L)+FWT(R)),其中 : : :表示连接。不难推出其逆变换为 U F W T ( L : R ) = U F W T ( L ) : ( U F W T ( R ) − U F W T ( L ) ) UFWT(L:R)=UFWT(L):(UFWT(R)-UFWT(L)) UFWT(L:R)=UFWT(L):(UFWT(R)−UFWT(L))。
与FWT
此时需要实现的变换是 B [ i ] = ∑ i & j = i A [ j ] B[i]=\sum_{i\& j=i}A[j] B[i]=∑i&j=iA[j]。
与或运算类似,容易推出 F W T ( L : R ) = ( F W T ( L ) + F W T ( R ) ) : F W T ( R ) FWT(L:R)=(FWT(L)+FWT(R)):FWT(R) FWT(L:R)=(FWT(L)+FWT(R)):FWT(R), U F W T ( L : R ) = ( U F W T ( L ) − U F W T ( R ) ) : U F W T ( R ) UFWT(L:R)=(UFWT(L)-UFWT(R)):UFWT(R) UFWT(L:R)=(UFWT(L)−UFWT(R)):UFWT(R)。
以上两变换又称FMT(快速莫比乌斯变换),又称高维前缀和。
异或FWT
这个比较奇怪,反正我想不到。此时需要实现的变换是 B [ i ] = ∑ ∣ i ∩ j ∣ ≡ 0 ( m o d 2 ) A [ j ] − ∑ ∣ i ∩ j ∣ ≡ 1 ( m o d 2 ) A [ j ] B[i]=\sum_{|i\cap j|\equiv 0\pmod 2}A[j]-\sum_{|i\cap j|\equiv 1\pmod 2}A[j] B[i]=∑∣i∩j∣≡0(mod2)A[j]−∑∣i∩j∣≡1(mod2)A[j]。
变换是
F
W
T
(
L
:
R
)
=
(
F
W
T
(
L
)
+
F
W
T
(
R
)
)
:
(
F
W
T
(
L
)
−
F
W
T
(
R
)
)
FWT(L:R)=(FWT(L)+FWT(R)):(FWT(L)-FWT(R))
FWT(L:R)=(FWT(L)+FWT(R)):(FWT(L)−FWT(R)),
U
F
W
T
(
L
:
R
)
=
U
F
W
T
(
L
)
+
U
F
W
T
(
R
)
2
:
U
F
W
T
(
L
)
−
U
F
W
T
(
R
)
2
UFWT(L:R)=\frac{UFWT(L)+UFWT(R)}{2}:\frac{UFWT(L)-UFWT(R)}{2}
UFWT(L:R)=2UFWT(L)+UFWT(R):2UFWT(L)−UFWT(R)(和差问题)。手推可验证正确。
*2018.11~12





















 2156
2156











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








