【算法学习】字符串 KMP算法、next数组性质

最新推荐文章于 2024-08-08 15:50:58 发布

memcpy0

最新推荐文章于 2024-08-08 15:50:58 发布

阅读量503

点赞数

分类专栏：字符串 # KMP

本文链接：https://blog.csdn.net/myrealization/article/details/107873647

版权

字符串同时被 2 个专栏收录

111 篇文章

订阅专栏

KMP

10 篇文章

订阅专栏

文章目录

1. 模板题目
2. 朴素的模式匹配算法
3. KMP算法
4. 字符串问题
5. 改进的KMP算法
6. next数组的性质

我们可以用字符串哈希解决特定字符子串的匹配，用前缀树解决 $n$ 个字符串中查找某个字符串的问题。现在，将学习一般性的模式匹配(Pattern Matching) 问题。

可以参考的网址：KMP算法详细讲解。

1. 模板题目

给出两个字符串 str 和 match ，长度分别为 N, M 。实现一个算法，如果 str 中含有子串 match ，返回 match 在 str 中的开始位置，否则返回 -1 。

如：

Input: str="acbc", match="bc"
Output: 2

Input: str="acbc", match="bcc"
Output: -1

如果 match 的长度大于 str ，str 必然不含有 match ，直接返回 -1 。如果 N > M ，要求算法复杂度为 $\text{O(N + M)}$ 。

2. 朴素的模式匹配算法

考虑暴力方法，从左到右，在 str 的所有字符中逐个匹配 match 的每个字符，如：str="abcxyz123" ，match="123" 。

第一次匹配，str[0] != match[0] ，后面的 match[1], match[2] 就不用比较了，直接移动到 str[1] 继续比较。总共比较 6 + 3 = 9 次就好了，其中前六次比较 match 的第一个字符，第 7 次比较 match 的 3 个字符。

不过这个例子比较特殊，两个字符串的字符基本上都不一样，复杂度差不多是 $\text{O(N + M)}$ ，已经是字符串匹配能够达到的最优复杂度了。如果字符串 str, match 符合这样的特征，暴力匹配是个不错的选择。

但是，情况比较坏时，比如 str="aaaaaaaaaaaab", match="aab" ，此时 match 的前 M - 1 个字符都很容易找到匹配，只有最后一个不匹配，则整体的复杂度就会退化成 $\text{O(NM)}$ 。因为主串中存在多个和模式串部分匹配的子串，因而引起指针 i 的多次回溯。

普通解法的时间复杂度这样高，是因为每次遍历到一个字符时，检查工作都从无到有，之前的遍历检查不能优化当前的遍历检查。

3. KMP算法

KMP算法是一种任何情况下都可以达到 $\text{O(N + M)}$ 的算法，它通过分析 match 的特征而对 match 进行预处理，从而在与 match 匹配的时候，利用已经得到的部分匹配的结果，跳过一些字符，达到快速匹配的目的。

下面介绍KMP算法的过程：

首先是生成 match 字符串的 nextArr 数组，数组的长度和 match 长度一样，nextArr[i] 的意义是：match[i] 之前的字符串 match[0...i - 1] 中，必须以 match[i - 1] 结尾的后缀子串(不能含有 match[0])，和必须以 match[0] 开头的前缀子串(不能含有 match[i - 1])，它们之间最长匹配长度是多少。这个长度就是 nextArr[i] 的值。这也是当模式串中位置 j 的字符和主串中相应字符 str[i] 失配时，在模式串中需要重新和主串该字符 str[i] 进行比较的字符的位置。

比如 match = "aaaab" ，nextArr[4] 的值是在 match[4] = 'b' 之前的字符串 "aaaa" ，这个字符串的后缀子串和前缀子串的最大匹配是 "aaa" ——就是后缀子串等于 match[1...3] = "aaa" 、前缀子串等于 match[0...2] = "aaa" 时，这时前缀和后缀不仅相等，而且是所有前缀和后缀的可能性中最大的匹配。所以 nextArr[4] = 3 。

再比如 match = "abclabcl ，nextArr[7] 的值是多少呢？match[7] = 'l' ，它之前的字符串是 "abclabc" 。根据定义，这个字符串的后缀子串和前缀子串的最大匹配为 "abc" ——也就是后缀子串等于 match[4...6] = "abc" 、前缀子串等于 match[0...2] = "abc" 时，这时前缀和后缀不仅相等，而且是所有前缀和后缀的可能性中的最大匹配。所以 nextArr[7] = 3 。

如何快速求出 nextArr 数组的问题，将在介绍KMP算法的大致过程之后进行说明。先假设已经有了 nextArr 数组，利用它加速 str, match 的匹配过程。
从 str[i] 字符出发，匹配到 j 位的字符发现与 match 中的字符不一致，就是说 str[i] == match[0] ，并且从这个位置开始一直可以匹配，直到发现 str[j] != match[j - i] 。如下图：

有了 match 字符串的 nextArr 数组，nextArr[j - i] 表示 match[0...j - i - 1] 这一段字符串中前缀和后缀的最长匹配。假设前缀是下图的 a 区域这一段，后缀是 b 区域这一段，再假设 a 区域的下一个字符是 match[k] ，如下图：

下一次匹配时，指向 str 的指针不会回溯到 str[i + 1] 重新和 match[0] 进行匹配，而是直接让 str[j] 和 match[k] 进行匹配检查。这对于 match 来说，相当于向右滑动让 match[k] 到 str[j] 同一个位置上，然后进行后续的检查。

KMP算法在匹配的过程中，一直进行这样的滑动匹配的过程，直到在 str 的某个位置把 match 完全匹配完，就说明 match 是 str 的子串。如果最后也没有匹配成功，就说明 str 中不含有 match 。

为什么这种做法是正确的呢？下图中，匹配到 A 字符和 B 字符才发生的不匹配，所以 c 区域等于 b 区域，b 区域又和 a 区域相等(nextArr 的含义如此)，所以 c 区域、a 区域是不需要检查的，必然会相等——直接把字符 C 滑动到字符 A 的位置开始检查即可。

这个过程相当于是从 str 的 c 区域中第一个字符重新开始的匹配过程，c 区域的第一个字符和 match[0] 匹配，并往右的过程。只是由于 c 区域一定等于 a 区域，所以省略了这个区域的匹配检查，直接从字符 A 和字符 C 往后继续匹配检查。

为什么开始的字符从 str[i] 直接跳到 c 区域后的第一个字符呢？中间这一段不需要检查吗？原因是：在这个区域中，从任何一个字符出发都肯定匹配不出 match 。

以上图为例，如果 d 区域开始的字符是不用检查区域的其中一个位置，如果那个位置能够开始匹配 match ，那么整个 d 区域都应该和从 match[0] 开始的区域匹配，即 d 区域和 e 区域长度一样，且两个区域的字符都相等。

这样，我们就会注意到，d 区域比 c 区域大，e 区域比 a 区域大。而且 d 区域对应到 match 字符串中是 d' 区域，也就是字符 B 之前的字符串的后缀，而 e 区域本身是 match 的前缀。所以对于 match 来说，相当于找到了 B 这个字符之前的字符串 match[0...j - i - 1] 的一个更大的前缀和后缀匹配——一个比 a 区域和 b 区域更大的前缀后缀匹配，e 区域和 d' 区域。

这与 nextArr[j - i] 的值是自相矛盾的，因为 nextArr[j - i] 的值代表的含义就是 match[0...j - i - 1] 字符串上最大的前后缀匹配长度。只要 match 的 nextArr 数组计算准确，就绝不会发生这种情况。所以，根本不会有更大的 d', e 区域，所以 d, e 区域也必然不会相等。

区间匹配过程中，指向 str 的 i 指针不会回溯、不会退回，而 match 则一直向右滑动，从而大大减少了匹配的次数。如果在 str 的某个位置完全匹配出 match ，整个过程就停止。否则就走到底，复杂度就是 $\text{O(N + M)}$ 。

代码如下：

public int getIndexOf(String s, String m) {
	if (s == null || m == null || m.length() < 1 || s.length() < m.length())
		return -1;
	char[] ss = s.toCharArray();
	char[] ms = m.toCharArray();
	int si = 0, mj = 0;
	int[] next = getNextArray(ms);
	while (si < ss.length && mj < ms.length) {
		if (ss[si] == ms[mj]) {
			++si;
			++mj;
		} 
		else if (next[mj] == -1) ++si;
		else mj = next[mj];
	}
	return mj == ms.length ? si - mj : -1;
}

最后是最关键的地方，快速求出 match 字符串的 nextArr 数组，有的也把 nextArr 数组称为部分匹配表。同时，也要证明得到 nextArr 数组的时间复杂度是 $\text{O(M)}$ ：

对于 match[0] 来说，它之前没有字符，所以 nextArr[0] 定义为 -1 ；
对于 match[1] 来说，它之前有 match[0] ，但是这里定义：任何子串的后缀不能包含第一个字符 match[0] ，所以 match[1] 之前只有长度为 0 的后缀字符串，所以 nextArr[1] = 0 。
对于 match[i], i > 1 来说，求解过程如下：
- 因为是从左到右依次求解 nextArr ，所以在求解 nextArr[i] 时，nextArr[0...i - 1] 的值都已经求出。假设 match[i] 字符是下图的 A 字符，match[i - 1] 为下图的 B 字符。
- 通过 nextArr[i - 1] 的值可以知道 B 字符前的字符串的最长前缀和后缀匹配区域，上图的 l 区域为最长匹配的前缀子串，k 区域为最长匹配的后缀子串，字符 C 为 l 区域后的字符。然后看字符 C 与字符 B 是否相等。
- 如果字符 C 和字符 B 相等，那么 A 字符之前的字符串的最长前缀和后缀匹配就可以确定，前缀子串为 l 区域 + C 字符，后缀子串为 k 区域 + B 字符。则 nextArr[i] = nextArr[i - 1] + 1 ；
- 如果字符 C 和字符 B 不相等，将看字符 C 之前的字符串的前缀和后缀匹配情况，假设字符串 C 是第 cn 个字符 (match[cn]) ，那么 nextArr[cn] 就是其最长前缀和后缀匹配长度。如下图，其中，m 和 n 区域分别是字符 C 之前的字符串的最长匹配后缀和前缀区域，是通过 nextArr[cn] 的值确定的。当然，两个区域是相等的：
  
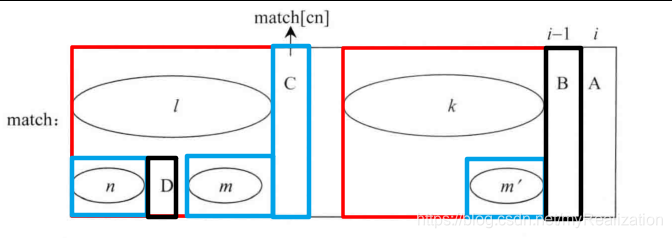
  m' 区域为 k 区域最右的区域，且长度与 m 区域一样，因为 k 区域和 l 区域是相等的，所以 m, m' 区域也是相等的。字符 D 为 n 区域的后一个字符，接下来比较字符 D 是否与字符 B 相等：
1. 如果相等，A 字符之前的字符串的最长前缀和后缀匹配区域就可以确定，前缀为 n 区域 + D 字符，后缀子串为 m' 区域 + B 字符，令 nextArr[i] = nextArr[cn] + 1 。
2. 如果不等，继续往前跳到字符 D，之后的过程与跳到字符 C 类似，一直进行这样的过程，跳的每一步都会有一个新的字符与 B 比较，就像 C 和 D 字符一样。只要有相等的情况，nextArr[i] 的值就可以确定。
- 如果向前跳到最左 match[0] 的位置，此时 nextArr[0] == -1 。说明字符 A 之前的字符串不存在前缀和后缀匹配的情况，则令 nextArr[i] = 0 。如果在字符串匹配的过程中在 match[i] 处失配，则需要从 match[0] 处重新开始匹配 (如 str="searbtring", match="search")。
- 用这种不断往前跳的方式，可以计算出正确的 nextArr[i] 值的原因，是因为每到一个位置 cn ，nextArr[cn] 的意义表示它之前字符串的最大匹配长度。具体过程见下面的 getNextArray 方法。

代码：

public int[] getNextArray(char[] ms) {
	if (ms.length == 1) return new int[] {-1};
	int[] next = new int[ms.length];
	next[0] = -1;
	next[1] = 0;
	int pos = 2;
	int cn = 0;
	while (pos < next.length) {
		if (ms[pos - 1] == ms[cn])
			next[pos++] = ++cn;
		else if (cn > 0) cn = next[cn];
		else next[pos++] = 0;
	}
	return next;
}

上面的代码中，while 循环就是求解 nextArr 数组的过程，这个循环的次数不会超过 $\text{2M}$ 这个数量。两个量其中一个为 pos 量，一个为 pos - cn 量。对于 pos 量来说，从 2 开始又必然不会超过 match 的长度；pos - cn 中，pos <= M - 1 ，cn >= 0 ，所以 pos - cn <= M - 1 。