目录
高等数学(1)函数、极限、导数
1,直积(笛卡尔乘积)
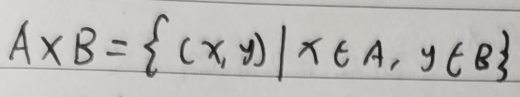
2,e的推导

3,柯西极限存在准则

4,间断点
书上间断点的定义是,f(x)在处不连续,则
为间断点。我个人感觉,数学分析上的定义更准确:f(x)在
的某邻域内有定义,且f(x)在
处不连续,则
为间断点。
间断点有2类,第一类只有可去间断点和跳跃间断点,第二类包括但不限于无穷间断点和振荡间断点。
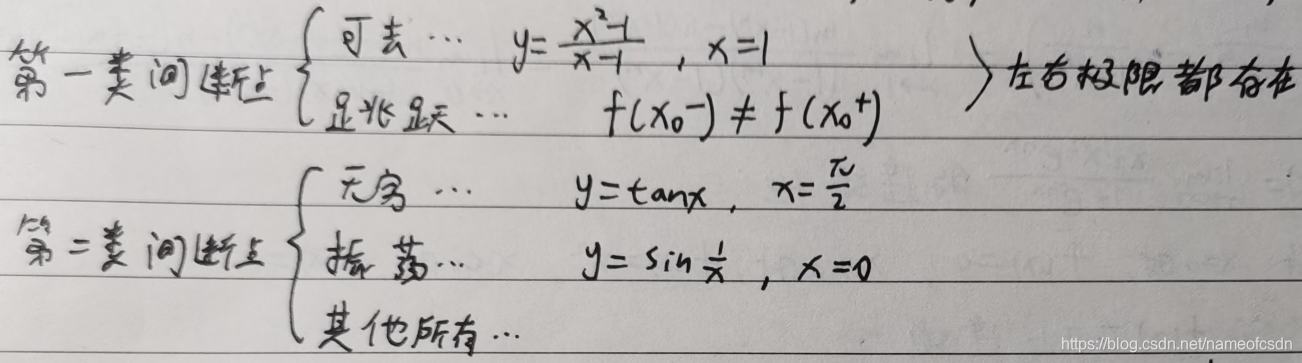
5,一致连续性

6,压缩映射、利普希茨条件
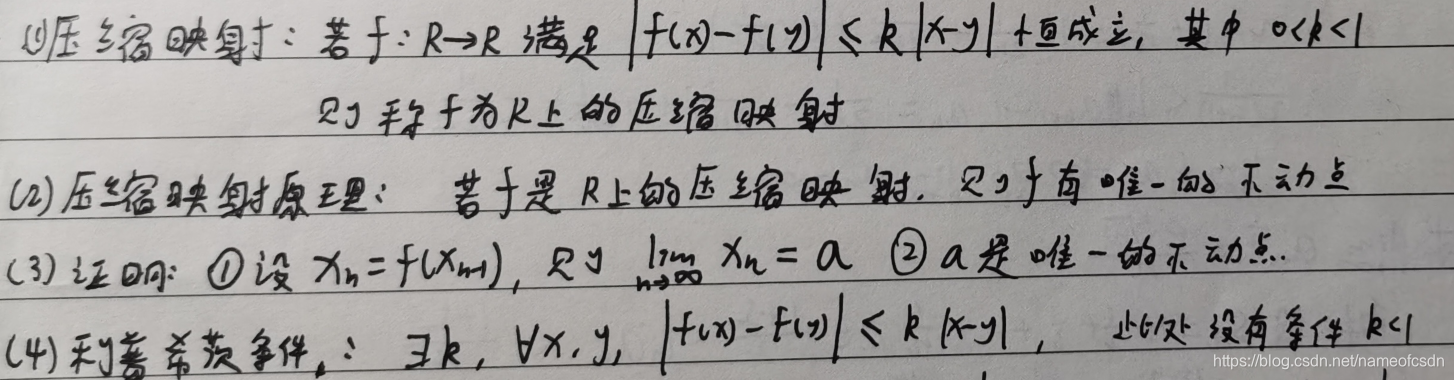
7,求导公式
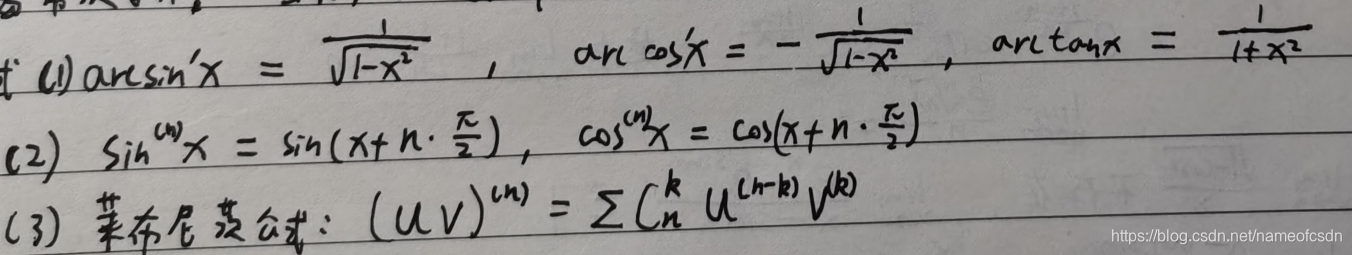
8,无穷大、无界变量
无穷大是无界变量,但无界变量不一定是无穷大
高等数学(2)函数、极限、导数题目
1, 是初等函数。
2, 是初等函数。
3,
4,
5,
6,
7,
8, 设f(x)在x=0处可导, , 又对
x,f(3+x)=3f(x), 求
解:
9, , 求
解: ,故
10,
11, , 找出一个数列
满足,当
时,
,(1)且
(2) 且
(3) 且
答案(1) (2)
(3)
12, 求 的连续性
解:求极限时,把x看成常数,当 x=0 时,
当 x>0 时, , 当 x<0时,
, 故
连续
13,设 连续,且
, 求
解:
(注意, 可能不存在)
14, 不成立
15, 设 求
解: 即
16, 不存在,
17, , 则
18, 若 , 则
19,
高等数学(3)中值定理、积分
1,费马引理
设f(x)在X₀的邻域U(X₀)内有定义且f'(X₀)存在。
若∀x∈U(X₀),f(X)≤f(X₀),则f'(X₀)=0 (驻点或稳定点)
2,罗尔定理
若f(x)在[a,b]上连续,在(a,b)上可导, 且f(a)= f(b),则彐ε∈(a,b),f'(ε)=0
3,拉格朗日中值定理
若f(X)在[a,b]上连续,在(a,b)上可导,则
也叫微分中值定理, 构造函数
4,柯西中值定理
若f(x),F(x)在[a,b]上连续,在(a,b)上可导,且∀x∈(a,b), 则
5,泰勒中值定理
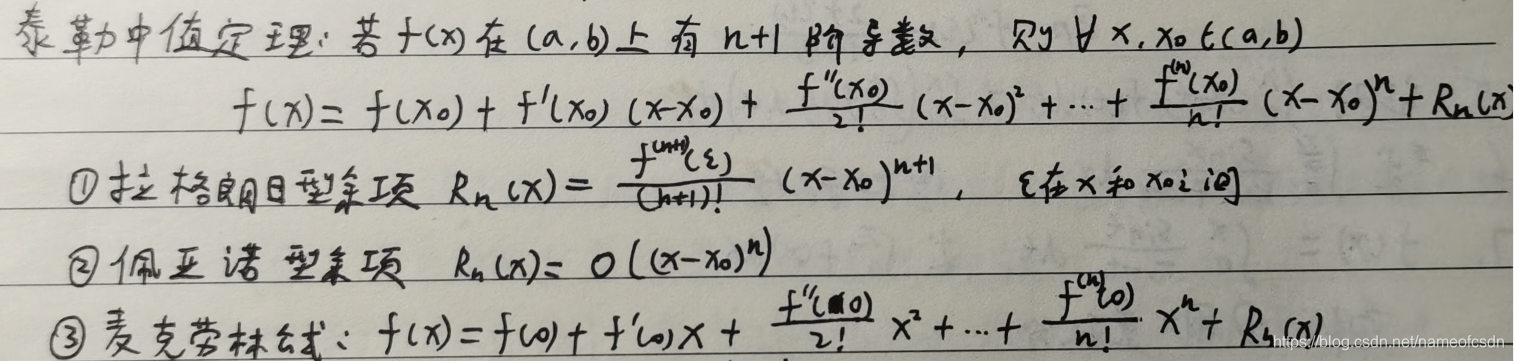
6,曲率、曲率半径
曲率K是曲率半径的倒数,
7,有理式、部分分式
有理式都可以化成3个部分的和:、
、
8,可积、有界
若f在[a,b]上可积,则若f在[a,b]上有界
9,反常积分、柯西主值
反常积分分为无穷区间反常积分、无界函数反常积分、混合反常积分。
无穷区间反常积分:
的柯西主值是
10,积分变换
设f的反函数是g,那么
对于无穷区间反常积分,如果反常积分存在,那么
,且根据柯西判别法可得
所以
11,中值定理题目
(1)若 , 则
(反证法)
(2)设f(x)在[a,b]上连续,在(a,b)上可导, , 证明
使
解: ,
(3)f(x)在[0,1]上二阶可导,且f(0)=f(1)=0,证明
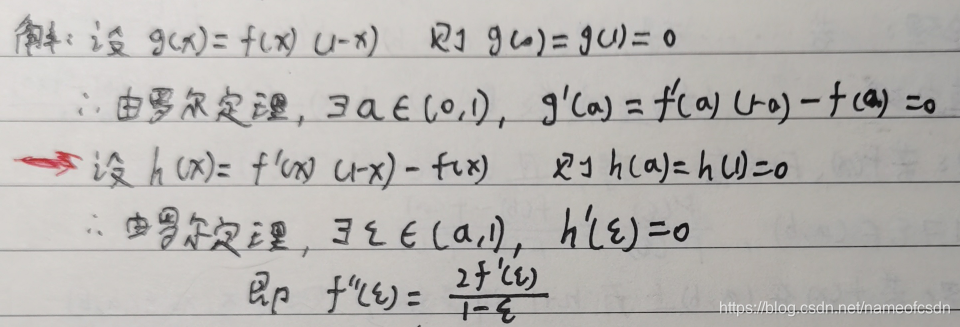
12,高等数学——积分
高等数学(4)级数
高等数学(5)几何应用


高等数学(6)多元函数微分
高等数学(7)重积分、含参变量的积分

5,重积分换元法
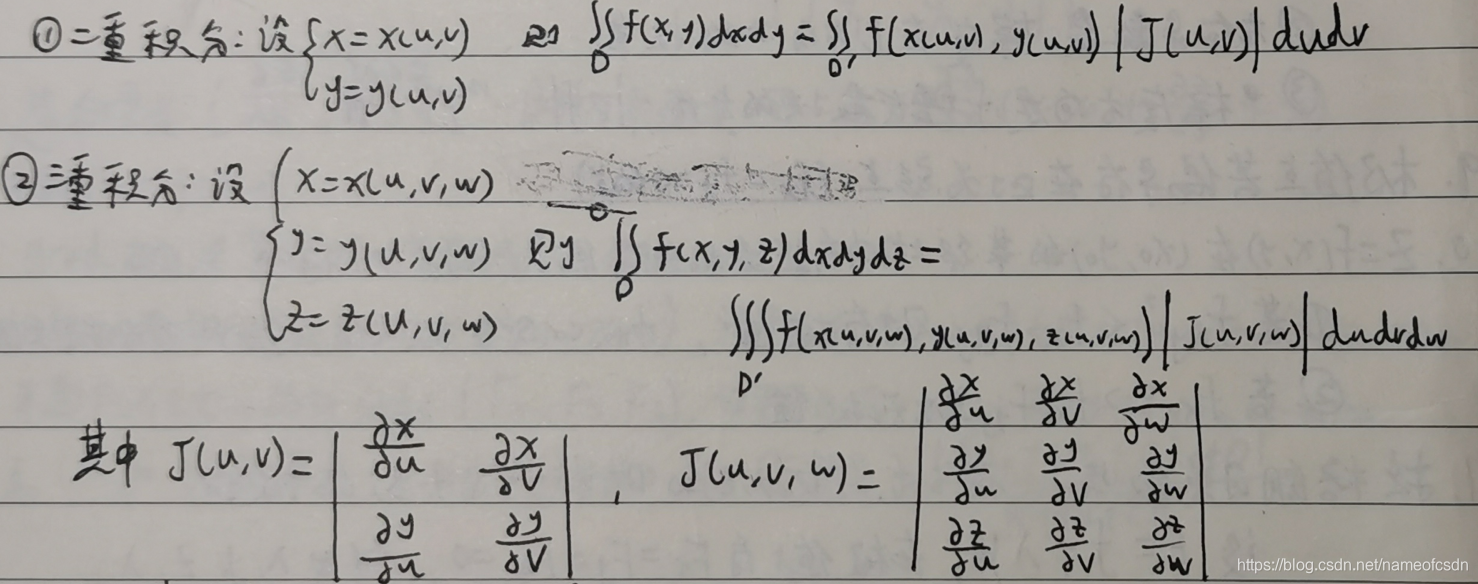

高等数学(8)曲线、曲面积分



1,斯托克斯(Stokes)公式


高等数学(9)微分方程
1,一阶常微分方程求解。
(1) 分离变量, 化为 则
(2) 齐次方程 , 设
则化为 (1)
(3) 可化为齐次的方程
若,设
化为(2)
若,设 t=a x+b y 化为 (1)
(4) 一阶线性微分方程常数变易法
对应齐次 , 解为
设 解出 u
2,二阶微分方程的降阶法
对于y''=f(x,y')和y''=f(y,y'),设t=y'化为1
3,线性微分方程的解的结构
(1)一阶线性:非齐次通解=非齐次特解+齐次通解
(2)二阶线性:齐次的解空间是二维线性空间,非齐次通解=非齐次特解+齐次通解
4,刘维尔公式
若y₁是y''+Py'+Qy=0的一个非0特解
则是与y₁线性无关的特解
5,二阶线性微分方程的常数变易法 y''+Py'+Qy=f
(1)设对应齐次的特解为y₁ 则设y=uy₁,化为2
(2)设对应齐次的特解为y₁、y₂ 则设y=u₁y₁+u₂y₂
并设u₁'y₁+u₂'y₂=0 ,则u₁'y₁'+u₂'y₂'= f直接解出u₁'、u₂'
6,
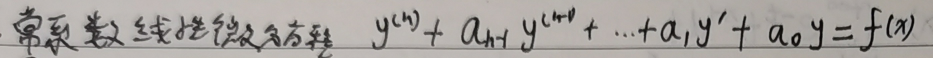


7,

8,
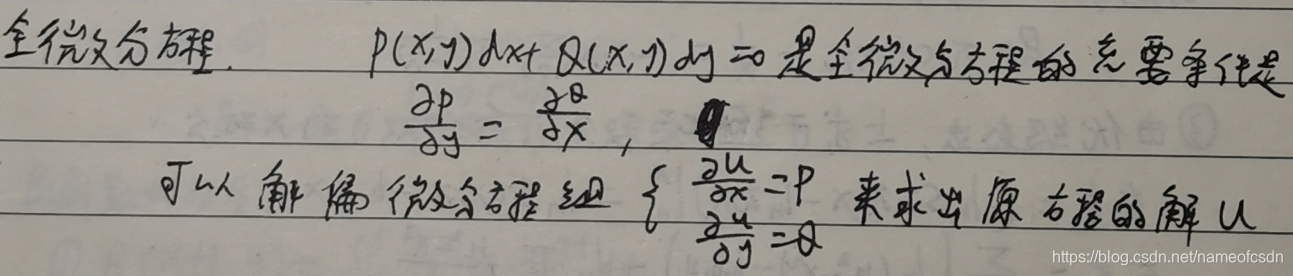























 1819
1819

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








