IQ使命2 Barcelona 巴塞罗那（色块覆盖）攻略-CSDN博客

本章规则：

就是要用所给的木块覆盖阴影区域，而且相邻的木块不能同色

（1）

（2）

（3）

（4）

（5）

（6）

除了第（1）（2）（6）关是只有2种颜色的，其他29个关卡都有3种颜色

（7）

（8）

（9）

（10）

我找到2种解法：

（11）

（12）

（13）

（14）

（15）

（16）

（17）

（18）

（19）

（20）

（21）

说实话这一关难到我了，虽然找到了可以把木块都放进阴影区域的方法，但是却没法使得相邻色块不同色。

所以我怀疑可能是因为惯性思维，所以我才想不到答案，只好借助我的编程能力来解决。

程序说明：

6*6的正方形分为目标阴影区域和非阴影区域，色块有3种颜色，8种形状，除了1*1的小正方形和2*2的大正方形之外，还有4个L型的块，以及1*2的横块和竖块，依次编号1-8。

给每个块标记一个核心点，用来表示块的位置：

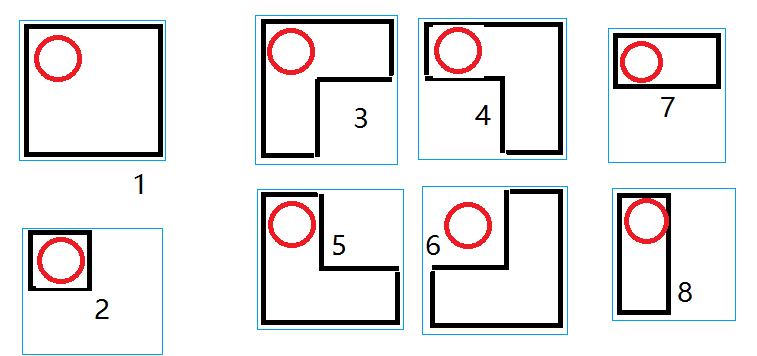
其中数字表示对形状的编号

每个块的位置用4个数字表示，空格用0表示，8个块依次是

1,2,3,4

1,0,0,0

1,2,3,0

1,2,0,4

1,0,3,4

0,2,3,4

1,2,0,0

1,0,3,0

如此便记录了每个块的形状，至于颜色就比较简单了，用1，2，3表示3种颜色就可以了

代码：

#include<iostream>
using namespace std;

int n;//一共n个块，n<20
int color[20]; //block[i]=1、2、3，表示3种颜色
int shape[20];//shape[i]=1、2、3、4、5、6，表示6种颜色
int list[6][6];//0是阴影区域，-1不是
int di[5] = { -1,0, 0, 1, 1 };//行偏移
int dj[5] = { -1,0, 1, 0, 1 };//列偏移
int dx[5] = { -1, 0, 0, -1, 1 };//行偏移
int dy[5] = { -1, 1, -1, 0, 0 };//列偏移
int p[9][4] =  //指向di和dj
{
	0, 0, 0, 0,
	1, 2, 3, 4,
	1, 0, 0, 0,
	1, 2, 3, 0,
	1, 2, 0, 4,
	1, 0, 3, 4,
	0, 2, 3, 4,
	1, 2, 0, 0,
	1, 0, 3, 0
};

bool ok(int i, int j,int k) //能否在(i,j)放第k个块
{
	int t[4], x, y;
	for (int a = 0; a < 4; a++)t[a] = p[shape[k]][a];
	for (int a = 0; a < 4; a++)
	{
		if (t[a] == 0)continue;
		x = i + di[t[a]], y = j + dj[t[a]];
		if (x<0 || x>5 || y<0 || y>5)return false;
		if (list[x][y])return false;	//此处实际上是数组的四层嵌套
		for (int b = 1; b <= 4; b++)
		{
			x = i + di[t[a]] + dx[b], y = j + dj[t[a]] + dy[b];
			if (x<0 || x>5 || y<0 || y>5)continue;
			if (list[x][y] == color[k])return false;
		}
	}
	return true;
}

bool trys(int k)	//第k个块能否放下去
{
	if (k > n)
	{
		cout << "答案（颜色）如下：\n";
		for (int i = 0; i<6; i++)
		{
			for (int j = 0; j < 6; j++)
			{
				if (list[i][j] == -1)cout << "  ";
				else cout << list[i][j] << " ";
			}
			cout << endl;
		}
		return true;
	}
	int t[4], x, y;
	for (int i = 0; i < 6; i++)for (int j = 0; j < 6; j++)if (ok(i, j, k))
	{
		for (int i = 0; i < 4; i++)t[i] = p[shape[k]][i];
		for (int a = 0; a < 4; a++)
		{
			if (t[a] == 0)continue;
			x = i + di[t[a]], y = j + dj[t[a]];
			list[x][y] = color[k];
		}
		if (trys(k + 1))return true;	//深度优先搜索
		for (int a = 0; a < 4; a++)//回溯
		{
			if (t[a] == 0)continue;
			x = i + di[t[a]], y = j + dj[t[a]];
			list[x][y] = 0;
		}
	}
	return false;
}

int main()
{
	n = 0;
	cout << "依次输入各个块的颜色，用1或2或3表示，以0结束\n";
	while (cin >> color[++n])if (color[n] == 0)break;
	n--;
	cout << "依次输入各个块的形状，用1-8表示\n";
	for (int i = 1; i <= n; i++)cin >> shape[i];
	cout << "依次输入36个格子各自是否属于目标阴影区域,0表示是，-1表示不是\n";
	for (int i = 0; i < 6; i++)for (int j = 0; j < 6; j++)cin >> list[i][j];
	trys(1);
	return 0;
}<iostream>
using namespace std;

int n;//一共n个块，n<20
int color[20]; //block[i]=1、2、3，表示3种颜色
int shape[20];//shape[i]=1、2、3、4、5、6，表示6种颜色
int list[6][6];//0是阴影区域，-1不是
int di[5] = { -1,0, 0, 1, 1 };//行偏移
int dj[5] = { -1,0, 1, 0, 1 };//列偏移
int dx[5] = { -1, 0, 0, -1, 1 };//行偏移
int dy[5] = { -1, 1, -1, 0, 0 };//列偏移
int p[9][4] =  //指向di和dj
{
	0, 0, 0, 0,
	1, 2, 3, 4,
	1, 0, 0, 0,
	1, 2, 3, 0,
	1, 2, 0, 4,
	1, 0, 3, 4,
	0, 2, 3, 4,
	1, 2, 0, 0,
	1, 0, 3, 0
};

bool ok(int i, int j,int k) //能否在(i,j)放第k个块
{
	int t[4], x, y;
	for (int a = 0; a < 4; a++)t[a] = p[shape[k]][a];
	for (int a = 0; a < 4; a++)
	{
		if (t[a] == 0)continue;
		x = i + di[t[a]], y = j + dj[t[a]];
		if (x<0 || x>5 || y<0 || y>5)return false;
		if (list[x][y])return false;	//此处实际上是数组的四层嵌套
		for (int b = 1; b <= 4; b++)
		{
			x = i + di[t[a]] + dx[b], y = j + dj[t[a]] + dy[b];
			if (x<0 || x>5 || y<0 || y>5)continue;
			if (list[x][y] == color[k])return false;
		}
	}
	return true;
}

bool trys(int k)	//第k个块能否放下去
{
	if (k > n)
	{
		cout << "答案（颜色）如下：\n";
		for (int i = 0; i<6; i++)
		{
			for (int j = 0; j < 6; j++)
			{
				if (list[i][j] == -1)cout << "  ";
				else cout << list[i][j] << " ";
			}
			cout << endl;
		}
		return true;
	}
	int t[4], x, y;
	for (int i = 0; i < 6; i++)for (int j = 0; j < 6; j++)if (ok(i, j, k))
	{
		for (int i = 0; i < 4; i++)t[i] = p[shape[k]][i];
		for (int a = 0; a < 4; a++)
		{
			if (t[a] == 0)continue;
			x = i + di[t[a]], y = j + dj[t[a]];
			list[x][y] = color[k];
		}
		if (trys(k + 1))return true;	//深度优先搜索
		for (int a = 0; a < 4; a++)//回溯
		{
			if (t[a] == 0)continue;
			x = i + di[t[a]], y = j + dj[t[a]];
			list[x][y] = 0;
		}
	}
	return false;
}

int main()
{
	n = 0;
	cout << "依次输入各个块的颜色，用1或2或3表示，以0结束\n";
	while (cin >> color[++n])if (color[n] == 0)break;
	n--;
	cout << "依次输入各个块的形状，用1-8表示\n";
	for (int i = 1; i <= n; i++)cin >> shape[i];
	cout << "依次输入36个格子各自是否属于目标阴影区域,0表示是，-1表示不是\n";
	for (int i = 0; i < 6; i++)for (int j = 0; j < 6; j++)cin >> list[i][j];
	trys(1);
	return 0;
}