主成分分析（PCA）

目录

一、算法概述

二、实验原理

三、算法实现

3.1导入数据

 3.2 用PCA进行降维

3.3 结果可视化

3.4完整代码展示：

四、总结分析

---

一、算法概述

主成分分析（PCA）是一种基于统计学的数据分析方法，旨在利用正交变换将原始数据转换为一系列线性不相关的变量，即主成分。这些主成分按照方差大小进行排序，第一主成分具有最大的方差，后续主成分依次递减。通过选择前几个主成分，我们可以在减少数据维度的同时，保留原始数据的主要信息。 

本次实验旨在通过主成分分析（PCA）方法对一个实际数据集进行降维处理，探索数据的内在结构和特征。主成分分析是一种常用的数据降维技术，它可以将高维数据转化为低维数据，同时保留原始数据的主要信息。

二、实验原理

PCA的主要原理包括：

1. 数据标准化：为了消除不同变量之间的量纲差异，需要对原始数据进行标准化处理，使得每个变量的均值为0，标准差为1。
2. 计算协方差矩阵：利用标准化后的数据计算协方差矩阵，协方差矩阵反映了不同变量之间的线性关系。
3. 计算特征值和特征向量：对协方差矩阵进行特征值分解，得到一组特征值和对应的特征向量。特征值表示数据在对应特征向量方向上的方差，特征向量则是新坐标系的基向量。
4. 选择主成分：按照特征值的大小，选择最大的几个特征值对应的特征向量作为主成分。这些主成分能够尽可能多地解释原始数据的方差。
5. 数据转化：通过将原始数据与所选主成分进行线性组合，得到转化后的数据。这些转化后的数据具有更低的维度，但仍然保留了原始数据的主要信息。

三、算法实现

3.1导入数据

准备数据：导入Scikit-learn库中的鸢尾花数据集

from sklearn import datasets
import matplotlib.pyplot as plt
import numpy as np
from sklearn.decomposition import PCA
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
# 鸢尾花的数据集
iris = datasets.load_iris()
print(iris)

 输出鸢尾花的数据集结果图如下：

 3.2 用PCA进行降维

X=iris['data']
y=iris['target']
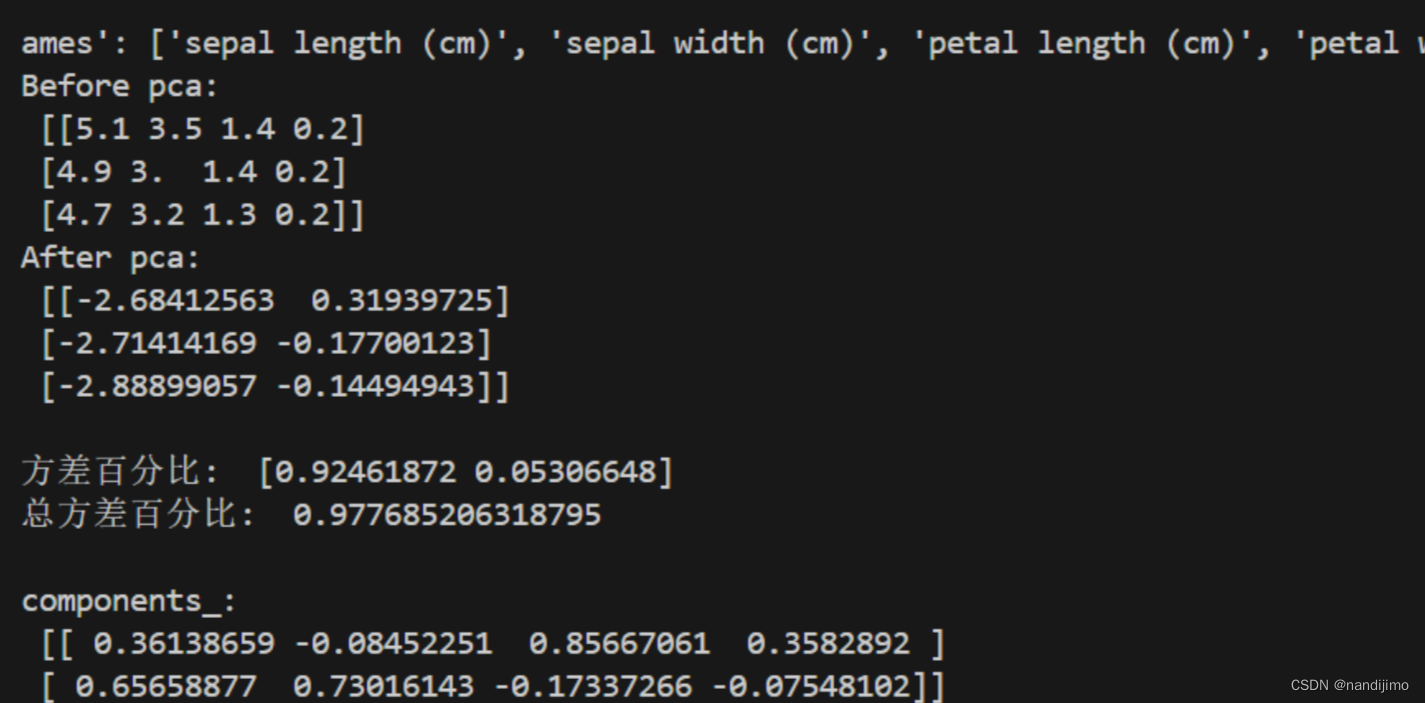
print('Before pca: \n', X[:3,:])# 前三行，所有列
 
pca_1 = PCA(n_components=2) # 指定主成分数量初始化  将数据降为2维
X_red_1 = pca_1.fit_transform(X) # fit并直接得到降维结果 
 
# 这里只展示前三行的结果以示对比
print('After pca: \n', X_red_1[:3, :],'\n')
 
# 查看各个特征值所占的百分比，也就是每个主成分保留的方差百分比
print('方差百分比: ', pca_1.explained_variance_ratio_)    
 
# 当前保留总方差百分比；
 
print('总方差百分比: ',pca_1.explained_variance_ratio_.sum(),'\n')
 
# 线性变换规则
print('components_: \n', pca_1.components_)

因为主成分数量为2，PCA处理过后，数据从四维变成二维，实现降维。结果如下所示： 

 

3.3 结果可视化

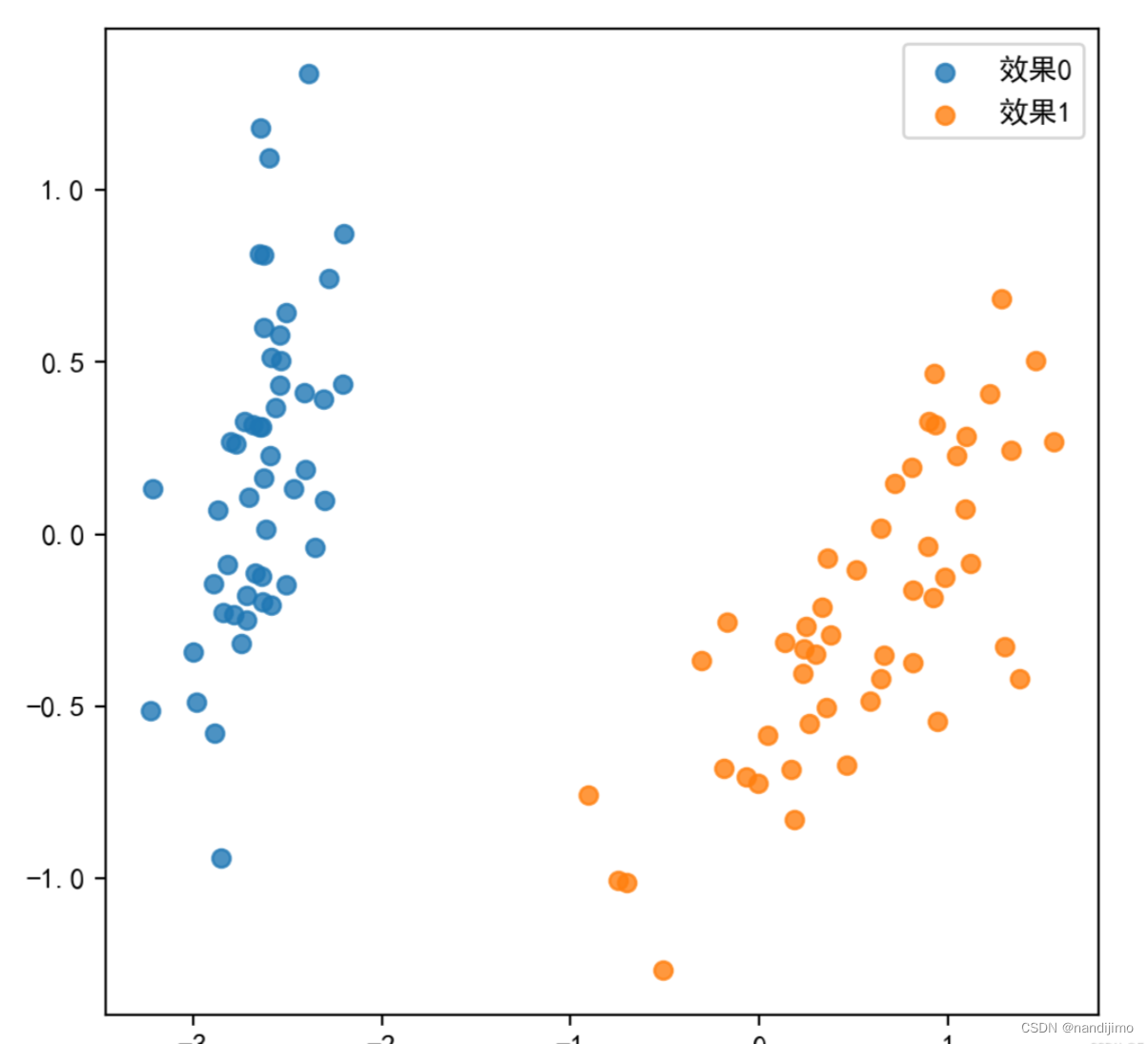
#结果可视化
plt.figure(figsize=(6,6))    
for i in range(2):
    plt.scatter(x=X_red_1[np.where(y==i),:][0][:,0], y=X_red_1[np.where(y==i),:][0][:,1], alpha=0.8, label='效果%s' % i)
plt.legend()
plt.show()

运行结果图： 

 

3.4完整代码展示：

from sklearn import datasets
import matplotlib.pyplot as plt
import numpy as np
from sklearn.decomposition import PCA
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
# 鸢尾花的数据集
iris = datasets.load_iris()
print(iris)
 
X=iris['data']
y=iris['target']
print('Before pca: \n', X[:3,:])# 前三行，所有列
 
pca_1 = PCA(n_components=2) # 指定主成分数量初始化  将数据降为2维
X_red_1 = pca_1.fit_transform(X) # fit并直接得到降维结果 
 
# 这里只展示前三行的结果以示对比
print('After pca: \n', X_red_1[:3, :],'\n')
 
# 查看各个特征值所占的百分比，也就是每个主成分保留的方差百分比
print('方差百分比: ', pca_1.explained_variance_ratio_)    
 
# 当前保留总方差百分比；
 
print('总方差百分比: ',pca_1.explained_variance_ratio_.sum(),'\n')
 
# 线性变换规则
print('components_: \n', pca_1.components_)
#结果可视化
plt.figure(figsize=(6,6))    
for i in range(2):
    plt.scatter(x=X_red_1[np.where(y==i),:][0][:,0], y=X_red_1[np.where(y==i),:][0][:,1], alpha=0.8, label='效果%s' % i)
plt.legend()
plt.show()

四、总结分析

通过本次实验，我们成功地将一个包含多个变量的鸢尾花的数据集进行了主成分分析。实验结果表明，前几个主成分能够解释原始数据的大部分方差，而后面的主成分对方差的解释能力较弱。因此，我们可以通过选择前几个主成分来降低数据的维度，同时保留原始数据的主要信息。

本次实验验证了主成分分析在数据降维方面的有效性。通过降低数据的维度，我们可以简化数据分析过程，提高计算效率，并去除噪声和冗余信息。此外，主成分分析还具有完全无参数限制的优点，不需要人为设定参数或根据经验模型进行干预，最后结果只与数据相关。

然而，主成分分析也存在一些局限性。例如，它是一种线性降维方法，无法处理非线性关系；同时，如果数据中存在异常值或噪声，可能会对分析结果产生一定影响。因此，在实际应用中，我们需要根据具体问题和数据特点选择合适的数据降维方法。