数学建模之图论

概览

1. 问题引入与分析
2. 图论的基本概念
3. 最短路问题及算法
4. 最小生成树及算法
5. 旅行售货员问题
6. 模型建立与求解

1. 问题引入与分析

1） 98年全国大学生数学建模竞赛B题“最佳灾情巡视路线”中的前两个问题是这样的：

今年(1998年)夏天某县遭受水灾. 为考察灾情、组织自救，县领导决定，带领有关部门负责人到全县各乡（镇）、村巡视. 巡视路线指从县政府所在地出发，走遍各乡（镇）、村，又回到县政府所在地的路线.
a. 若分三组（路）巡视，试设计总路程最短且各组尽可能均衡的巡视路线。
b. 假定巡视人员在各乡（镇）停留时间T=2小时，在各村停留时间t=1小时，汽车行驶速度V =35公里/小时. 要在24小时内完成巡视，至少应分几组；给出这种分组下最佳的巡视路线.

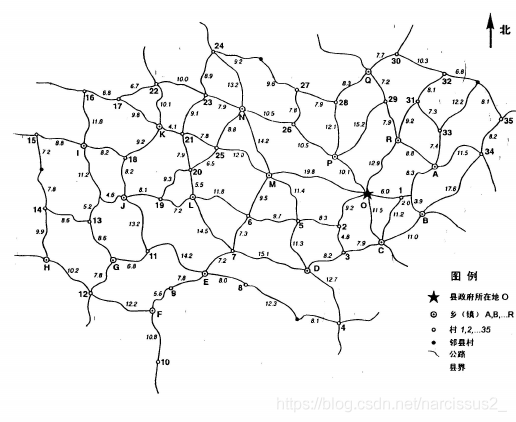
公路边的数字为该路段的公里。

2) 问题分析：

本题给出了某县的公路网络图，要求的是在不同的条件下，灾情巡视的最佳分组方案和路线.
将每个乡（镇）或村看作一个图的顶点，各乡镇、村之间的公路看作此图对应顶点间的边，各条公路的长度（或行驶时间）看作对应边上的权，所给公路网就转化为加权网络图，问题就转化图论中一类称之为旅行售货员问题，即在给定的加权网络图中寻找从给定点O出发，行遍所有顶点至少一次
再回到点O，使得总权（路程或时间）最小.

本题是旅行售货员问题的延伸－多旅行售货员问题.
本题所求的分组巡视的最佳路线，也就是m条经过同一点并覆盖所有其他顶点又使边权之和达到最小的闭链（闭迹）.
如第一问是三个旅行售货员问题，第二问是四个旅行售货员问题.
众所周知，旅行售货员问题属于NP完全问题，即求解没有多项式时间算法.
显然本问题更应属于NP完全问题. 有鉴于此，一定要针对问题的实际特点寻找简便方法，想找到解决此类问题的一般方法是不现实的，对于规模较大的问题可使用近似算法来求得近似最优解.

2. 图论的基本概念

1. 图的概念
2. 赋权图与子图
3. 图的矩阵表示
4. 图的顶点度
5. 路和连通

1) 图的概念

定义 一个图G是指一个二元组(V(G),E(G))，其中:

1. V ( G ) = { v 1 , v 2 , . . . , v ν } V (G) = \{ v_1,v_2,...,v_ν \} V(G)={v1​,v2​,...,vν​}是非空有限集，称为顶点集，其中元素称为图G的顶点.
2. $E(G)$是顶点集$V(G)$中的无序或有序的元素偶对$(v_i,v_j)$ 组成的集合，即称为边集,其中元素称为边.

定义 图G的阶是指图的顶点数|V(G)|, 用 v来表示；图的边的数目|E(G)|用ε 来表示.
用 $G=(V(G),E(G))$ 表示图，简记 $G=(V,E)$.也用$v_i{v}_j$ 来表示边$(v_i,v_j)$.

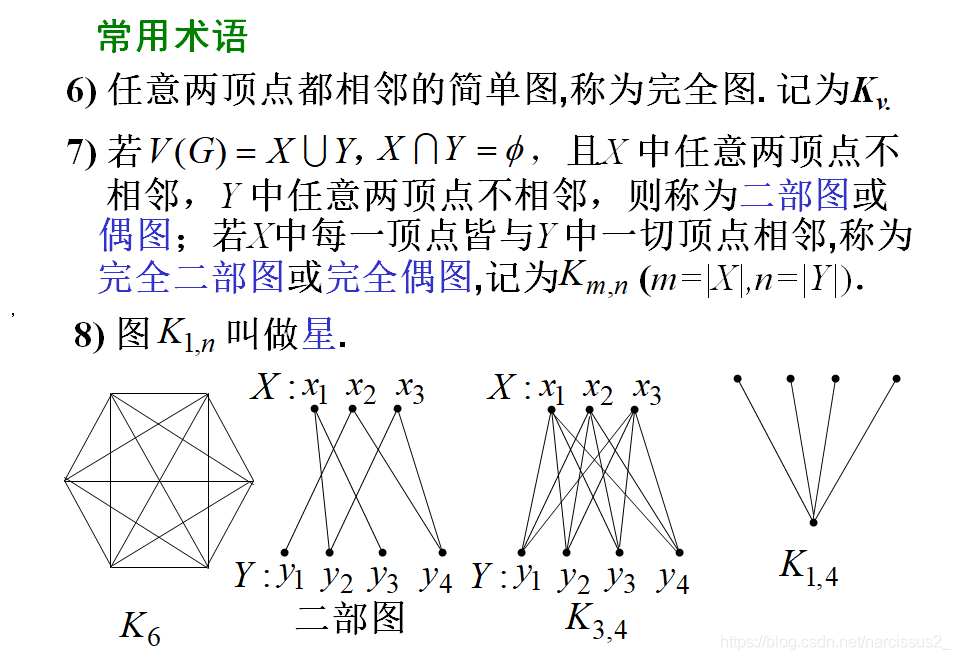
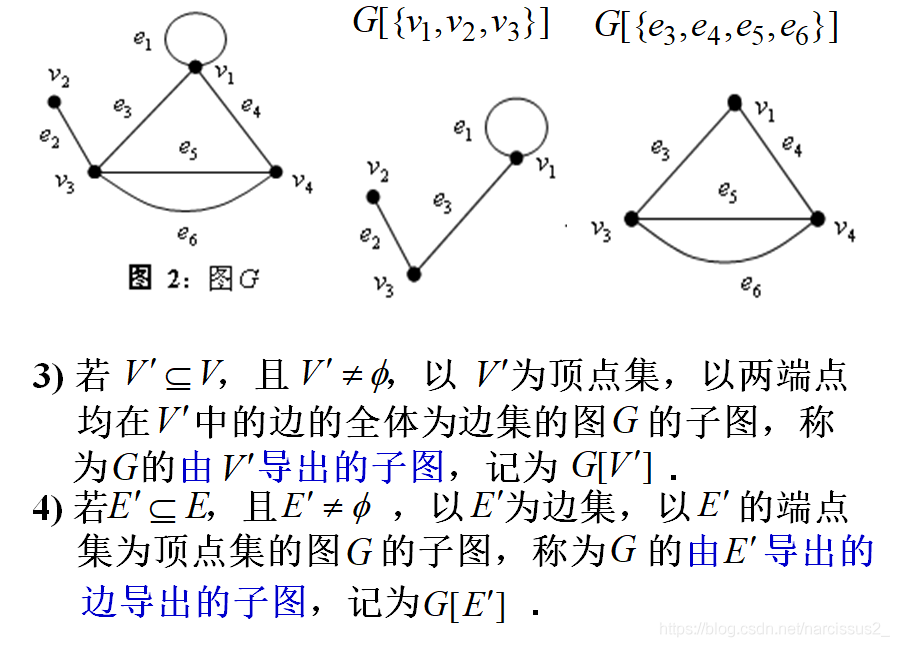
3. 最短路

Dijkstra算法

略

Floyd算法

算法的基本思想

直接在图的带权邻接矩阵中用插入顶点的方法依次构造出ν 个矩阵$D(1)、D(2)、\dots 、D(\nu )$，使最后得到的矩阵 $D(\nu )$成为图的距离矩阵，同时也求出插入点矩阵以便得到两点间的最短路径。
（I）求距离矩阵的方法.
（II）求路径矩阵的方法.
（III）查找最短路路径的方法.

Floyd有两个矩阵，一个是D矩阵（代表距离），一个是R矩阵（代表中介点）

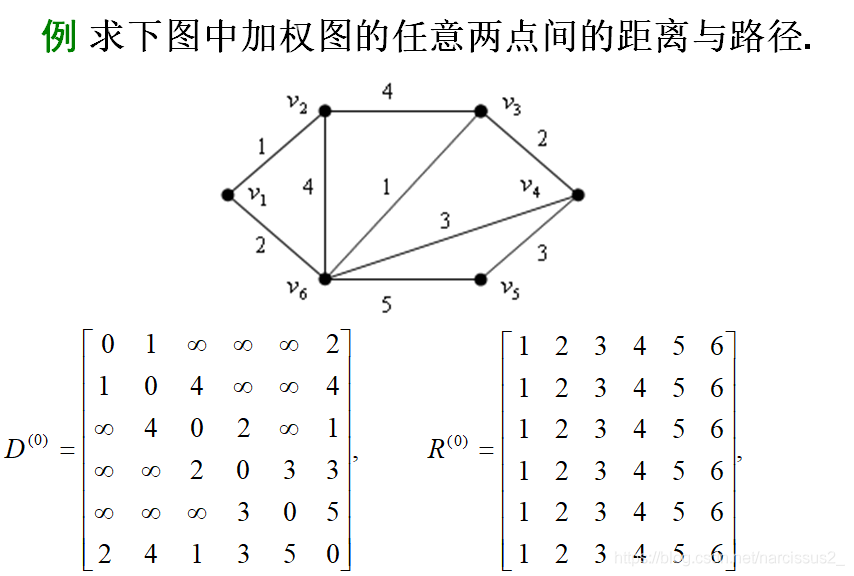
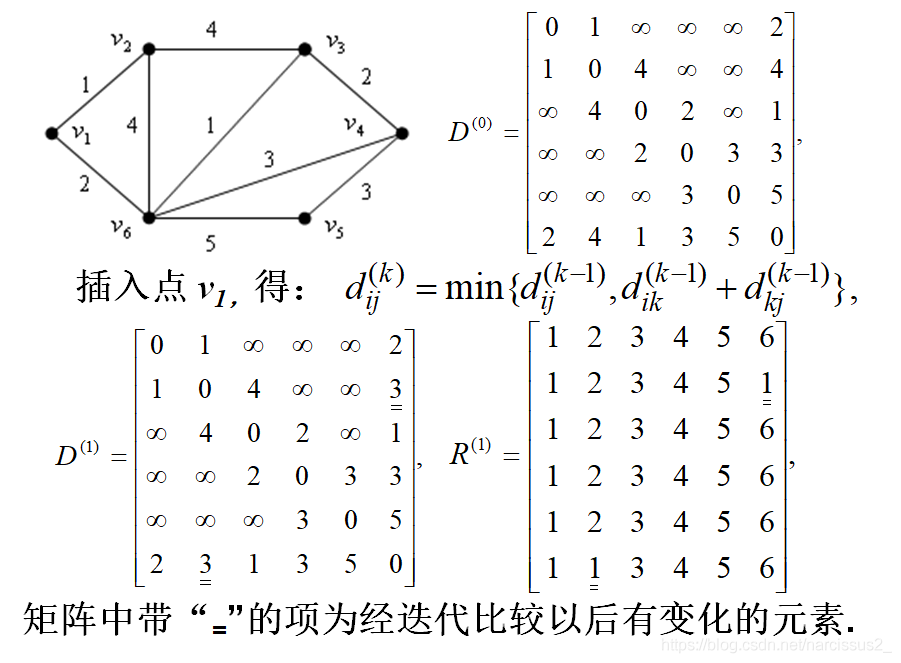
• 在这里相当于$v_1$被打通了，此时$v_1$就可以作为中介点连接。
• 于是遍历和$v_1$连接的点，例如此时遍历到$v_2$。
• 然后再以$v_2$为基准，遍历和$v_1$连接的点。
• 所有遍历到的点都尝试一下是否可以变化距离矩阵，如果可以变化，那么再他们的中介点矩阵上打入"1"的标记。
  
  
  
  
  
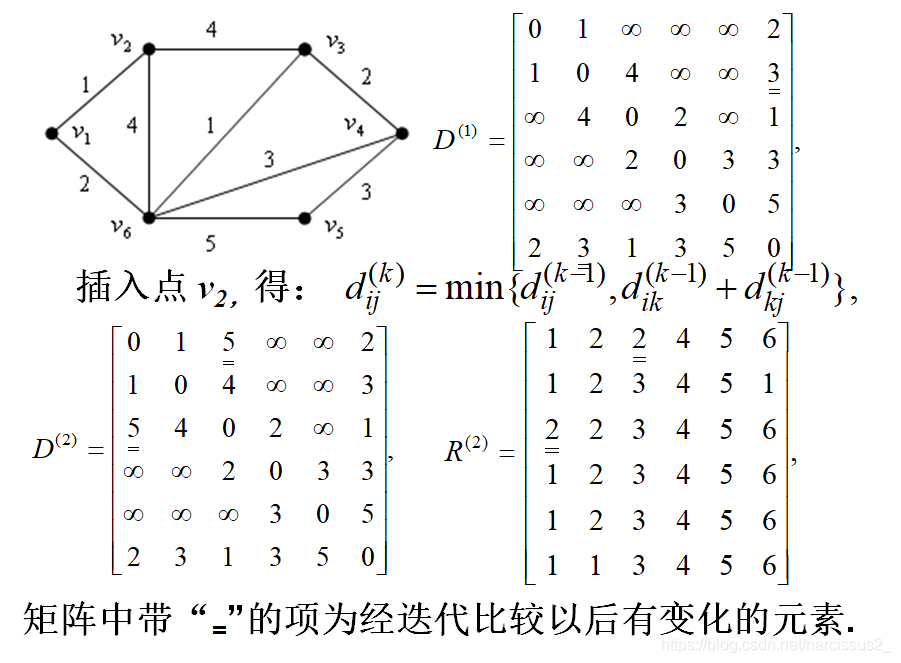
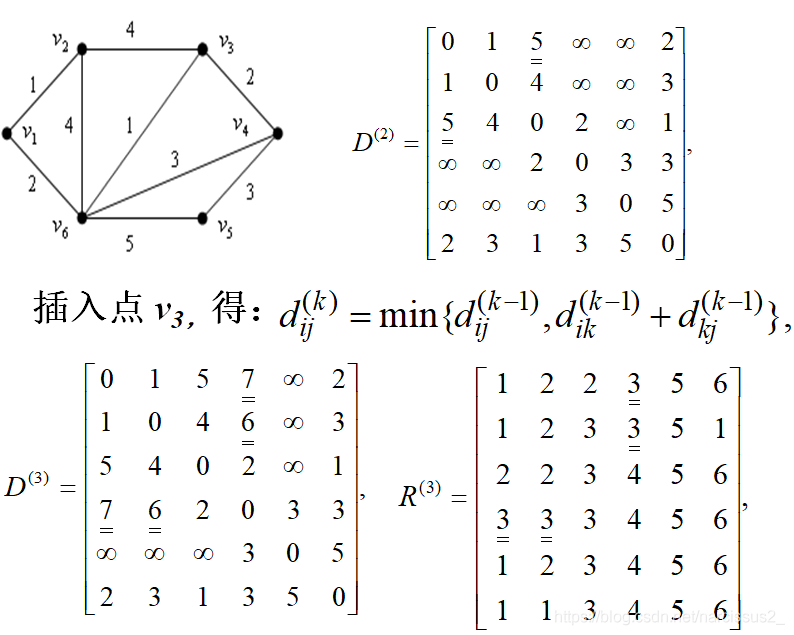
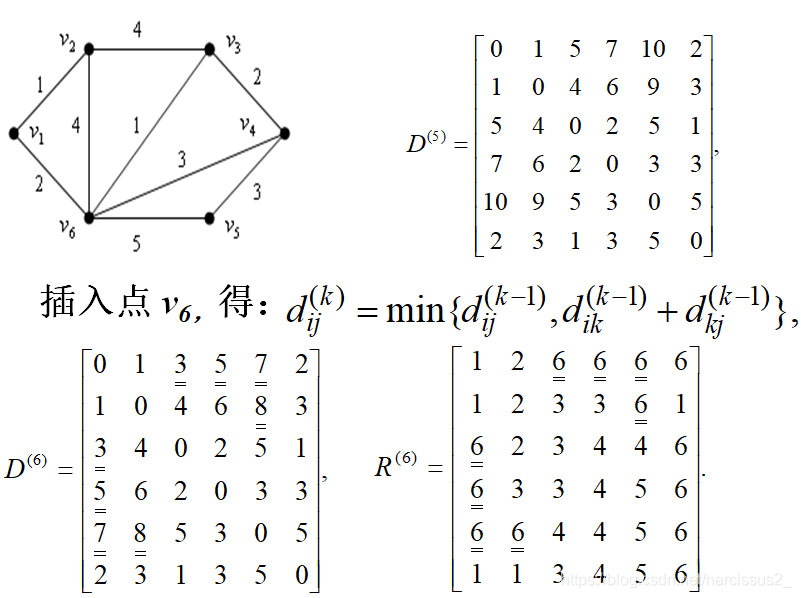
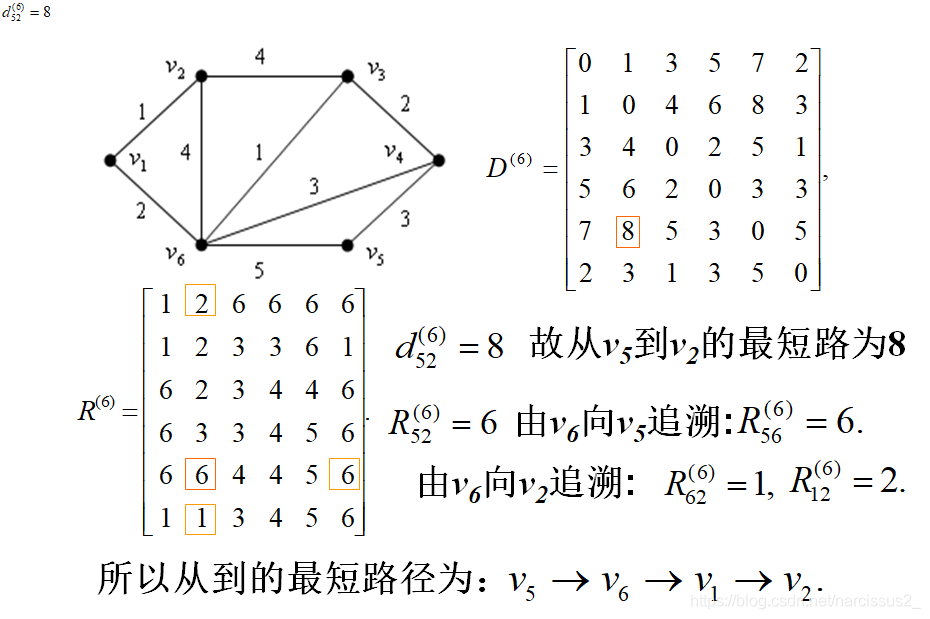
  这里的逻辑是这样的:
• $R_{52}=6$，说明从5到2的下一个点为6
• $R_{62}=1$，说明6到2的下一个点为1
• $R_{12}=2$，说明1到2的下一个点为2
• 所以路径为$v_5\to v_6\to v_1\to v_2$

最小生成树

（略）