Painter's Problem
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 3462 | Accepted: 1710 |
Description
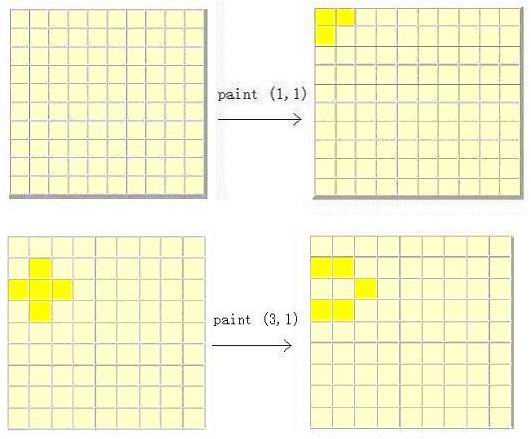
There is a square wall which is made of n*n small square bricks. Some bricks are white while some bricks are yellow. Bob is a painter and he wants to paint all the bricks yellow. But there is something wrong with Bob's brush. Once he uses this brush to paint brick (i, j), the bricks at (i, j), (i-1, j), (i+1, j), (i, j-1) and (i, j+1) all change their color. Your task is to find the minimum number of bricks Bob should paint in order to make all the bricks yellow.

Input
The first line contains a single integer t (1 <= t <= 20) that indicates the number of test cases. Then follow the t cases. Each test case begins with a line contains an integer n (1 <= n <= 15), representing the size of wall. The next n lines represent the original wall. Each line contains n characters. The j-th character of the i-th line figures out the color of brick at position (i, j). We use a 'w' to express a white brick while a 'y' to express a yellow brick.
Output
For each case, output a line contains the minimum number of bricks Bob should paint. If Bob can't paint all the bricks yellow, print 'inf'.
Sample Input
2 3 yyy yyy yyy 5 wwwww wwwww wwwww wwwww wwwww
Sample Output
0 15
Source
╮(╯▽╰)╭,因为数组开的不够大RE了几次
#include<iostream>
#include<cstring>
using namespace std;
const int mm=937;
int map[mm][mm+1];
int ans[mm];
int var,equ;
int max_ans;
void debug();
void swap(int&a,int &b)
{
int tmp;tmp=a;a=b;b=tmp;
}
/*
int abs(int x)
{
if(x<0)return -x;return x;
}*/
int gcd(int a,int b)
{
int t;
while(b!=0)
{
t=b;b=a%b;a=t;
}return a;
}
int lcm(int a,int b)
{
return a*b/gcd(a,b);
}
void dfs(int z,int dep,int k,int kans)
{
ans[var-dep]=z;
if(dep==k)
{
for(int i=var-k-1;i>=0;i--)
{
int tmp;
tmp=map[i][var]%2;
for(int j=i+1;j<var;j++)
if(map[i][j])
tmp=(tmp-(map[i][j]*ans[j])%2+2)%2;
ans[i]=(tmp/map[i][i])%2;if(ans[i])++kans;
}
if(kans<max_ans)max_ans=kans;
//cout<<"ans="<<kans<<endl;
}
else
{
dfs(1,dep+1,k,kans+1);dfs(0,dep+1,k,kans);
}
}
int Guss()
{
int k,col;;
for(k=0,col=0;k<equ&&col<var;k++,col++)
{/**行变换消元*/
int max_i=k;
for(int i=k+1;i<equ;i++)
if(map[i][col]>map[max_i][col])max_i=i;
if(max_i!=k)
{//for(int i=k;i<var+1;i++)好像也OK
for(int i=col;i<var+1;i++)//是K不是col因为k--;
swap(map[k][i],map[max_i][i]);
}
/**除去对角线0,列变换*/
for(int i = 0; i <equ; ++i)//每一行主元素化为非零
if(!map[i][i])
{
int j;
for(j = i+1;j<var;++j)
if(map[i][j])
break;
if(j == var)
break;
for(int kk = 0;kk < equ; ++kk)
swap(map[kk][i],map[kk][j]);
}
/**遇到对角线0,k退1*/
if(map[k][col]==0)
{
k--;continue;
}
/**消元*/
for(int i=k+1;i<equ;i++)
if(map[i][col]!=0)
{
int LCM=lcm(map[k][col],map[i][col]);
int ta,tb;
ta=LCM/map[i][col];tb=LCM/map[k][col];
if(map[i][col]*map[k][col]<0)tb=-tb;
for(int j=col;j<var+1;j++)
{
map[i][j]=((map[i][j]*ta)%2-(map[k][j]*tb)%2+2)%2;
}
}
// cout<<"k="<<k<<endl;
}
//debug();
///判断回代
for(int i=k;i<equ;i++)
if(map[i][col])return -1;
if(var==k)
for(int i=k-1;i>=0;i--)
{
int tmp;
tmp=map[i][var]%2;
for(int j=i+1;j<var;j++)
if(map[i][j])
tmp=(tmp-(map[i][j]*ans[j])%2+2)%2;
ans[i]=(tmp/map[i][i])%2;if(ans[i])max_ans++;
}
else
{ max_ans=999999;
dfs(1,1,var-k,1);dfs(0,1,var-k,0);
}
return 0;
}
void debug()
{
for(int i=0;i<var;i++)
{for(int j=0;j<var+1;j++)
cout<<map[i][j];
cout<<"\n";
}
}
int main()
{
int cas,num;
cin>>cas;
char s;
while(cas--)
{memset(map,0,sizeof(map));
memset(ans,0,sizeof(ans));
max_ans=0;
cin>>num;
var=equ=num*num;
for(int i=0;i<num;i++)
{
for(int j=0;j<num;j++)
{ map[i*num+j][i*num+j]=1;
if(i!=0)map[i*num+j][(i-1)*num+j]=1;
if(j!=0)map[i*num+j][i*num+j-1]=1;
if(i!=num-1)map[i*num+j][(i+1)*num+j]=1;
if(j!=num-1)map[i*num+j][i*num+j+1]=1;
cin>>s;
if(s=='y')map[i*num+j][var]=0;
else map[i*num+j][var]=1;
//cout<<map[i*num+j][var];
//cout<<"i="<<i<<"j="<<j<<endl;
}
}
int flag=Guss();
//debug();
if(flag==-1)cout<<"inf\n";
else
{
cout<<max_ans<<"\n";
}
}
}
























 14万+
14万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








