Radar Installation
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 75342 | Accepted: 16859 |
Description
Assume the coasting is an infinite straight line. Land is in one side of coasting, sea in the other. Each small island is a point locating in the sea side. And any radar installation, locating on the coasting, can only cover d distance, so an island in the sea can be covered by a radius installation, if the distance between them is at most d.
We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.
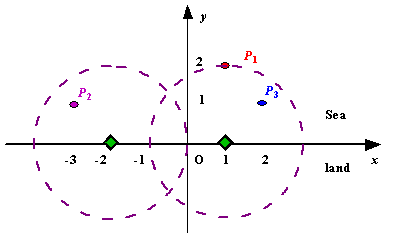
Figure A Sample Input of Radar Installations
We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.

Figure A Sample Input of Radar Installations
Input
The input consists of several test cases. The first line of each case contains two integers n (1<=n<=1000) and d, where n is the number of islands in the sea and d is the distance of coverage of the radar installation. This is followed by n lines each containing two integers representing the coordinate of the position of each island. Then a blank line follows to separate the cases.
The input is terminated by a line containing pair of zeros
The input is terminated by a line containing pair of zeros
Output
For each test case output one line consisting of the test case number followed by the minimal number of radar installations needed. "-1" installation means no solution for that case.
Sample Input
3 2 1 2 -3 1 2 1 1 2 0 2 0 0
Sample Output
Case 1: 2 Case 2: 1
题解:
首先对于每一个岛以雷达的半径作圆找出与x轴的左交点和右交点(如果这个岛与x轴没有交点,就说明雷达不能将所有的岛全部覆盖),如果雷达不能将所有的岛全部覆盖,此时输出-1。否则,将右交点从小到大依次排序,因为要想得到最少需要安装的雷达数,所以雷达最初的位置处于从小到大的第一个右交点上,再依次往后判断,如果下一个岛的左交点在雷达所在的位置的左边,就说明雷达得探测范围能覆盖这个岛,否则不能。如果不能,在这个岛与x轴的右交点上再安装一个雷达,依次类推,直到雷达能覆盖所有的岛时结束。
#include<cstdio> #include<cmath> #include<algorithm> using namespace std; struct note{ double left; double right; }q[1010]; bool cmp(note a , note b) { return a.right < b.right; } int main() { int n,i,l=1; double r,x,y; while(scanf("%d %lf",&n,&r)!=EOF) { int ans = 0; if(n == 0 && r == 0) break; for(i = 0 ; i < n ; i++) { scanf("%lf %lf",&x,&y); if( y > r) ans = -1; q[i].left = x - sqrt(r * r - y * y); // 左交点 q[i].right = x + sqrt(r * r - y * y); // 有交点 } if(ans == -1){ printf("Case %d: %d\n",l++,ans); continue; } sort(q,q+n,cmp); double xx = q[0].right; //第一个雷达所在位置 int falg = 1; for(i = 1 ; i < n ; i++) { if(q[i].left > xx) // 判断前面所安装的雷达是否能覆盖到这个岛 { xx = q[i].right; //更新雷达所在位置 falg++; // 对雷达数计数 } else continue; } printf("Case %d: %d\n",l++,falg); } return 0; }
























 1108
1108

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








