算法导论 4-7

1 题目

一个m×n的实数矩阵A，如果对所有i，j，k和l，1 <= i < k <=m和1 <= j < l <= n，有

A[i,j]+A[k,l]<=A[i,l]+A[k,j]

那么，此矩阵A为Monge矩阵。换句话说，每当我们从Monge矩阵中跳出两行和两列，并且考虑行列交叉处的4个元素，左上角与右下角元素的和小于等于左下角与右上角的和。a)证明一个矩阵为Monge阵，当且仅当对所有i=1，2，…，m-1和j=1，2，…，n-1，有

A[i,j]+A[i+1,j+1] <= A[i,j+1]+A[i+1,j]

b)下面的矩阵不是Monge阵。改变一个元素，把它变成Monge阵

37	23	22	32
21	6	7	10
53	34	30	31
32	13	9	6
43	21	15	8

c)假设f(i)是第i行包含最左端最小值的列的索引值。证明对任何的m×n Monge矩阵，有f(1)<=f(2)…<=f(m)

d)以下是一段关于分治算法的描述，用来计算m×n Monge矩阵A的每一行的最左端最小值：

构造一个包含所有A的偶数行的子矩阵A'。递归地计算A'中每一行的最左端最小值。然后计算A中奇数行的最左端最小值。

解释如何能在O(m+n)时间内计算出A的奇数行的最左端最小值？（假设偶数行的最左端最小值已知）

e)写出d部分所描述算法运行时间的递归式，并证明其解为O(m+nlgm)

2 分析与解答

a)

证明：

1. 必要性：设k=i+1，l=j+1，显然i，k，j，l满足Mango矩阵对于元素下标的假设，将k，l 带入Mango矩阵的不等式中，必要性得证
2. 充分性：当一个2×2矩阵满足a）中不等式时，是Monge矩阵。

   当一个2×k矩阵满足a）中不等式时，假设其是Monge矩阵，如果将此矩阵最右端扩展一 列，形成2×(k+1)矩阵，并且满足a)中的不等式，即

   A[1,k]+A[2,k+1] <= A[1,k+1]+A[2,k]

   由于原2×k矩阵是Monge矩阵，所以A[1,i]+A[2,k] <= A[1,k]+A[2,i]

   所以A[1,i]+A[2,k]-A[2,i] <= A[1,k]，所以A[1,i]+A[2,k]-A[2,i]+A[2,k+1] <= A[1,k+1]+A[2,k] ;

   所以A[1,i]+A[2,k+1] <= A[1,k+1]+A[2,i]，所以扩展的2×(k+1)矩阵是Monge矩阵，由 归纳法可知，满足题设条件的所有2×n矩阵是Monge矩阵。

   将满足题设条件的2×n扩展成m×n矩阵，并且m×n矩阵满足题设条件，那么根据上一步 的结论， 矩阵的任意两行都构成Monge矩阵 ，那么对于此m×n矩阵，就有对所有i，j， k和l，1 <= i < k <=m和1 <= j < l <= n，有A[i,j]+A[k,l]<=A[i,l]+A[k,j]，即证明 满足题设条件的m×n矩阵为Monge矩阵。

b)

用c)中结论，将第一行第2，3个元素交换即可

c)

证明：用反证法，假设1<=i<j<=m，有f(i)>f(j)，那么一定有，

A[i,f(j)]+A[j,f(i)]>min(A[i][1..n])+min(A[j][1…n])=A[i,f(i)]+A[j,f(j)]，这是与Monge矩阵的定义相悖的，所以，若一个矩阵是Monge矩阵，必然满足题目结论

d)

沿用c)中的标识，f(i)表示第i行最左端最小值的列索引。如果偶数行的f(i)已知，那么奇数行j的最左端最小值只需在f(j-1)和f(j+1)之间搜索（第一行在1到f(2)之间搜索），若m为奇数，那么m行最左端最小值要在f(m-1)到n中搜索。不难理解，最坏情况下，总的搜索次数是f(2)+∑_i=2^n/2(f(2i)-f(2i-2))[+n-f(n-1)] =f(2)+f(4)-f(2)+f(6)-f(4)…=n加上访问每行的代价为O(m)，所以总代价为O(m+n)

e)

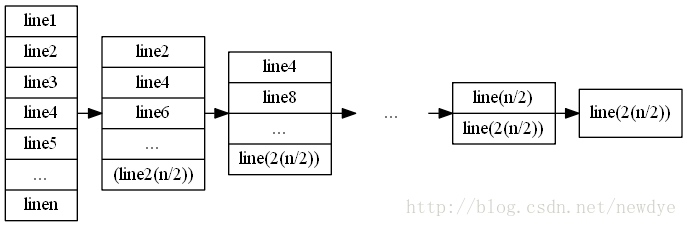
T(m)=T(m/2)+D(m)+C(m)，其中，D(m)是将矩阵分割成偶数行的操作，其时间代价为D(m)=O(m)；C(m)是从f(i-1)至f(i+1)之间找到奇数行的最小值，其每次递归的代价为n_i ，T(m)=T(m/2)+O(m)+∑ n_i ，简单画出递归树：

可见，在分解和解决完成后，每步合并都会在n步内完成，也就是n_i =O(n)，通过递归树可以看到需要合并的步骤数是Θ(lgm)，所以C(m)=O(nlgm)。再由递归树得到，T(m)=m∑_i=0^lgm-1(1/2ⁱ )+O(nlgm)=2(1+m)+O(nlgm)=O(m)+O(nlgm)=O(m+nlgm)