贝叶斯学习（Bayesian Learning）基础篇

前言

本文将基于UoA的课件介绍机器学习中的贝叶斯。

涉及的英语比较基础，所以为节省时间（不是full-time，还有其他三门课程，所以时间还是比较紧的），只在我以为需要解释的地方进行解释。

此文不用于任何商业用途，仅仅是个人学习过程笔记以及心得体会，侵必删。

Motivation and Introduction

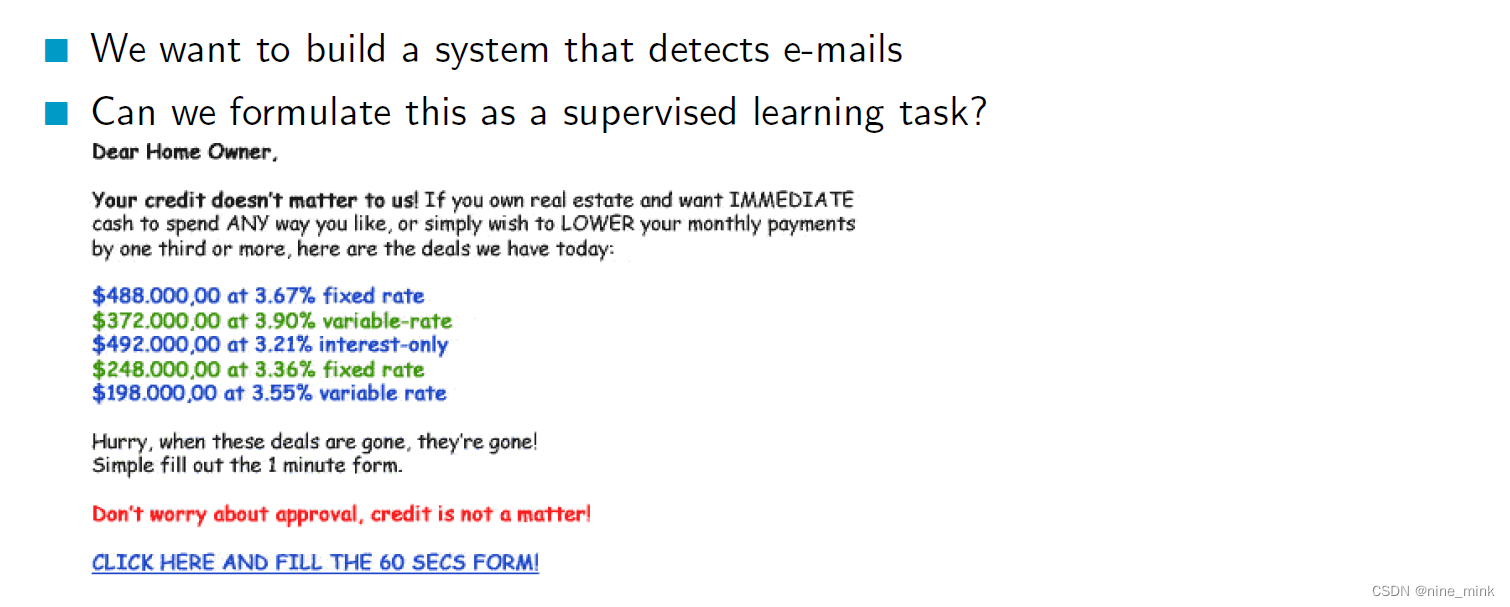
Think about Spam Filtering.

Lead in, 比较简单，不多说了。





$P(Y)$是事件Y的先验概率，即在考虑观测数据之前我们对事件Y发生的概率的估计。$P(X|Y)$是在事件Y发生的条件下观测到数据X的概率，称为事件Y的似然度。$P(X)$是数据X发生的边际概率，也称为证据。

贝叶斯公式的含义可以用以下步骤概括：

1. 先根据我们的先验知识（$P(Y)$）对事件Y的发生概率进行估计。

2. 观测到数据X之后，根据我们对数据的了解，计算出在事件Y发生的条件下，数据X出现的概率（$P(X|Y)$）。

3. 通过计算边缘概率$P(X)$，将$P(Y)$和$P(X|Y)$结合起来，计算出事件A在观测到数据B之后的后验概率$P(Y|X)$。

4. 根据计算出的后验概率$P(Y|X)$，来做出决策或者预测等等。

因此，贝叶斯公式提供了一个非常有用的工具，使我们能够基于先验知识和观测数据来更新我们对事件的认知，从而得到更准确的预测和推断。

先验概率

先验概率可以理解为在考虑观测数据之前，我们对某个事件发生的概率的主观估计或预测。比如我们可以通过过去的经验、个人经验、相关数据等信息，对某个事件的发生概率进行估计，这个估计就是先验概率。

举个例子，假设我们想预测某个人得某种疾病的概率。在这种情况下，我们可以基于先前的流行病学数据、个人基因、生活方式等信息，估计这个人得病的先验概率。如果我们知道这种疾病的发病率大约是1%，那么我们可以将先验概率估计为0.01。

另一个例子是，在进行一项实验之前，我们可以基于过去的实验数据和经验来估计某个事件的概率。例如，假设我们要进行一次抛硬币的实验，并且我们相信这个硬币是均匀的。在这种情况下，我们可以将正面朝上的概率估计为0.5，这就是硬币正面朝上的先验概率。

需要注意的是，先验概率是主观的，并且可能会因人而异。它也可能会受到信息的影响而发生变化。因此，在一些情况下，先验概率可能需要根据实际情况不断地更新和调整。

后验概率

后验概率是在考虑了观测数据之后，我们对某个事件发生概率的更新或修正。换句话说，后验概率是在考虑了新的数据或证据之后，我们对某个事件的概率进行更新的概率。

举个例子，假设我们要预测某个人得某种疾病的概率，并且我们知道这种疾病的发病率大约是1%。如果我们进行了一次检查，并且结果显示这个人确实得了这种疾病，那么我们可以使用贝叶斯公式来计算在已知这个人确实得了这种疾病的情况下，他得这种疾病的后验概率。在这种情况下，后验概率将是一个更精确的估计，因为它考虑了实际观测数据的影响。

另一个例子是，在进行一项抛硬币的实验之后，如果我们得到了一些观测数据，例如硬币正面朝上的次数或比例，我们可以使用贝叶斯公式来计算正面朝上的后验概率。在这种情况下，后验概率也是在考虑了观测数据之后对硬币正面朝上概率的更新或修正。

需要注意的是，后验概率是基于先验概率和观测数据计算得出的，并且可能会因不同的先验概率或观测数据而有所不同。通过不断地更新和修正先验概率和观测数据，我们可以获得更准确和可靠的后验概率估计。

后验概率可以被视为先验概率的更新或修正。

似然度

在贝叶斯统计中，似然度（likelihood）是指给定一些模型参数和观测数据时，观测数据出现的概率。简单来说，似然度描述的是模型和数据之间的关系，它是一种在已知模型参数的情况下，描述数据的概率。

举个例子，假设我们想要使用一个线性模型来预测房价，该模型有一个参数向量w和一个截距b。我们使用一个数据集包含了一些房屋的特征和实际售价来训练该模型。在训练过程中，我们需要通过最小化损失函数来确定最佳的参数向量和截距，使得模型可以最好地拟合数据。

在这个例子中，似然度描述的是给定参数向量w和截距b的情况下，数据集中房价的分布情况。我们可以使用高斯分布或其他概率分布来描述房价分布，然后通过最大化似然度来寻找最佳的参数向量和截距。最大化似然度的过程是在确定最佳参数向量和截距的过程中非常重要的一步。

另一个例子是，在进行信号处理或机器学习任务时，我们经常需要对数据进行分类。在分类问题中，似然度描述的是给定一些数据和一些假设的类别标签，数据属于每个类别的概率。我们可以使用似然度来计算每个类别的后验概率，然后选择具有最高后验概率的类别作为数据的预测类别。在这个例子中，似然度是对数据分类任务非常重要的一部分。

似然度和后验概率是不同的概念。后验概率是指在给定数据的情况下，模型参数的概率分布，而似然度是指在给定模型参数的情况下，数据的概率分布。这两个概念通常会在贝叶斯推断中一起出现，因为我们可以使用似然度和先验概率来计算后验概率。

似然度的实际意义是给定模型参数下，观测到当前数据的可能性大小。

如果我们有一组观测数据 $D=x_1,x_2,...,x_n$，假设这些数据是独立同分布的，我们可以使用一个概率分布 $P(x|\theta )$ 来描述这些数据的生成过程，其中 $\theta$ 是模型的参数。这个概率分布 $P(x|\theta )$ 称为似然函数，它描述的是给定模型参数 $\theta$ 下，数据 $D$ 出现的概率。因此，似然度的实际意义就是给定模型参数 $\theta$ 下，观测到当前数据 $D$ 的可能性大小。

在机器学习中，我们通常会使用似然度作为模型参数的优化目标

边际概率

边际概率可以理解为某个事件的概率，不考虑其他随机变量的影响。通俗地说，它描述的是一个事件在所有可能情况下出现的概率，而不管其他变量的取值如何。

Basic assumption

贝叶斯的基本假设是：感兴趣的量（如参数、预测值等）都是由概率分布所控制的，因此可以通过对概率分布进行推断来获得关于这些量的信息。同时，观察到的训练数据可以提供有关概率分布的信息。

这个假设的意思是，我们假设我们关注的任何事物都存在一个与之相关的概率分布，该分布控制了我们感兴趣的量的变化。例如，在机器学习中，我们可能会对参数的值、模型的输出或预测值感兴趣。在这种情况下，我们可以通过对概率分布进行推断来获得有关这些量的信息。

在这种假设下，我们可以使用贝叶斯定理来进行推断和预测。这个定理告诉我们如何通过观察到的数据来更新概率分布，并且可以将这些信息用于做出最优决策。

这种方法的优点在于，它能够利用观测到的数据来更新我们对事物的概率分布的认识，从而可以更加准确地进行预测和推断。同时，这种方法能够处理不确定性信息，能够更好地反映实际情况。

假设我们想要预测某个人患上某种疾病的概率。我们可以假设这个患病率是由一个二元概率分布所控制的，即在患病和不患病之间进行选择。

我们有一些先验信息，例如有关人群中患病率的平均值和标准差。然后我们对某些人进行测试，得到这些人是否患病的信息。通过这些信息，我们可以使用贝叶斯定理来更新我们对这个概率分布的认识，并预测其他人患病的可能性。

在这个例子中，贝叶斯的基本假设是：人们是否患病是由一个概率分布所控制的，并且我们可以使用观察到的数据来更新这个分布。我们使用贝叶斯定理来计算后验分布，该分布给出了一个人患病的可能性，基于我们对患病率的先验知识和我们观察到的数据。这个分布可以用来做出最优决策，例如决定是否给一个人进行进一步的测试或治疗。

让我们举一个更加具体的例子来说明贝叶斯基本假设的应用。

假设我们想要预测一篮子水果中苹果和橙子的数量。我们有一些先验知识，例如在水果店中苹果和橙子的比例通常是2:1。我们可以将这些知识表示为一个先验概率分布。

现在，我们随机地从这篮子水果中抽取了一些水果，观察到其中有多少个苹果和橙子。通过这些观察数据，我们可以使用贝叶斯定理来更新我们的概率分布，并计算出新的后验分布，该分布给出了苹果和橙子的数量的可能性。

在这个例子中，贝叶斯基本假设是：苹果和橙子的数量是由一个概率分布所控制的，并且我们可以使用观察到的数据来更新这个分布。我们使用贝叶斯定理来计算后验分布，该分布给出了苹果和橙子数量的可能性，基于我们对苹果和橙子比例的先验知识和我们观察到的数据。这个分布可以用来做出最优决策，例如决定将这些水果分成苹果和橙子的组别，或者预测下一个篮子水果中苹果和橙子的数量。

我们假设事件的发生是由概率分布所控制的，使用观察到的数据来更新这个分布，从而获得更加准确的预测和推断。

Relevance

虽然贝叶斯方法是一种基于概率的学习方法，但是它的基本思想也可以为我们理解其他不直接操作概率的学习方法提供有用的框架。

在贝叶斯方法中，我们通过计算先验概率和似然度来获得后验概率，从而推断模型参数或预测新数据。这里的关键在于概率的更新和修正过程，即根据新的数据来更新我们对参数或结果的信念。

类似地，其他的机器学习方法也可以通过对现有数据进行拟合来获得模型参数或预测新数据。虽然这些方法不涉及概率的计算，但它们也涉及到我们对数据的解释和理解。例如，在决策树或支持向量机等非概率方法中，我们通过在训练集上选择最优的分割点或超平面来拟合模型，从而得到一个可以泛化到新数据的模型。

贝叶斯方法的思想可以为我们提供一种理解其他机器学习方法的框架，即通过不同的方式来更新我们对数据的解释和理解，从而获得更好的模型和预测能力。

没有明确操作概率的方法，通常指那些不直接使用概率分布或贝叶斯公式来推断模型参数或进行预测的方法。这些方法可能是基于统计学或最优化理论的，它们可以通过最大似然估计、最小二乘法或其他优化算法来寻找最优解或模型参数。

举例来说，决策树是一种非概率的方法，它通过在训练数据中选择最优的分割点来构建树形结构，从而对新数据进行分类或回归。支持向量机也是一种非概率方法，它通过在数据空间中找到最优的超平面来进行分类或回归。

虽然这些方法没有直接使用概率分布或贝叶斯公式来推断参数或预测结果，但它们仍然可以使用概率的思想来解释它们的结果。例如，在决策树中，我们可以使用基尼不纯度或信息增益来衡量每个分割点的不确定性，从而选择最优的分割点。在支持向量机中，我们可以使用核函数来将数据从低维空间映射到高维空间，从而找到最优的超平面来进行分类或回归。

没有明确操作概率的方法并不意味着不涉及概率的思想，它们仍然可以使用概率的思想来解释和理解其结果。

Practical diculties

首先，贝叶斯方法需要事先对许多概率进行了解，例如先验概率和似然度，这些知识需要从领域专家、历史数据或实验数据中获取。如果这些信息不充分或不准确，将会影响到贝叶斯推断的准确性和可靠性。

其次，贝叶斯方法需要进行大量的计算，包括对多个概率进行更新和整合，这可能会导致计算复杂度的显著增加。对于复杂的模型和大量的数据，计算成本可能会非常高昂，需要使用高性能计算设备或并行计算方法。

此外，贝叶斯方法还需要面对一些统计学上的挑战，例如如何选择合适的先验概率、如何处理高维数据、如何避免过拟合等等。这些问题需要经验丰富的统计学家或数据科学家进行深入研究和解决。

尽管存在这些困难，贝叶斯方法仍然具有广泛的应用，尤其是在小数据集和高不确定性情况下，它可以提供一种准确和可靠的推断方法，为决策提供了有力的支持。

Bayes’ Theorem

Probability: random events

样本空间Ω（sample space）: 随机实验的所有结果的集合。在这里，每个结果都可以被认为是对实验结束时真实世界状态的完整描述。

事件集（event space）F: 一个集合，其元素A E F(称为事件)是Ω的子集(即，A C Ω是一个实验可能结果的集合)。

Probability measure（概率测度） 是一种用于描述概率空间（probability space）中随机事件的数学工具。概率空间由三个元素组成：样本空间（sample space）、事件空间（event space）和概率测度（probability measure）。

概率测度是一个函数，它将事件映射到一个实数上，表示该事件发生的可能性大小。概率测度必须满足以下三个性质：

1. 非负性：对于任意的事件A，概率测度P(A)必须大于等于0。

2. 规范化：对于样本空间Ω，概率测度P(Ω)必须等于1。

3. 可列可加性：对于任意可列个不相交的事件Ai（i=1,2,…），概率测度P(A1∪A2∪…)等于它们各自的概率测度之和。

通俗地说，概率测度就是一种用于度量事件发生概率大小的函数，它必须满足一些基本性质以保证它的有效性和可靠性。在概率论中，我们使用概率测度来定义随机变量的概率分布、计算事件发生的概率等。

例子:考虑抛一个六面骰子的事件。样本空间为Ω ={1,2,3,4,5,6}。我们可以在这个示例空间上定义不同的事件空间。例如，最简单的事件空间是平凡事件空间F = {0， Ω}。另一个事件空间是Ω所有子集的集合。对于第一个事件空间，满足上述要求的唯一概率测度为P(0) = 0, P(Ω) = 1。对于第二个事件空间，一个有效的概率度量是将事件空间中每个集合的概率赋值为，其中i为该集合的元素个数;例如，P({1,2,3,4}) =4/6 和 P({1,2,3})=3/6

考虑一个实验，我们抛10枚硬币，我们想知道正面朝上的硬币的数目。这里，样本空间Ω的元素是10个长度的正面和反面序列。例如，我们可能有Wo = < H, H,T, H,T, H, H,T, T) 属于 Ω。然而，在实践中，我们通常不关心获得任何特定的正面和反面序列的概率。相反，我们通常关心的是结果的实值函数，比如在10次投掷中出现正面的次数，或者出现反面的最长时间。在某些技术条件下，这些函数被称为随机变量。

Bayesian Learning

在贝叶斯学习中，我们假设有一个数据集D，需要从中推断出一个最佳的假设h。那么，如何理解“最佳”呢？在贝叶斯学习中，“最佳”通常是指条件概率P(h|D)最大的假设h，即给定数据集D后，假设h成立的概率最大。因此，在贝叶斯学习中，我们使用条件概率P(h|D)来定义最佳假设。这个条件概率可以通过贝叶斯定理计算得到，其中先验概率P(h)和似然度P(D|h)都需要考虑到。换句话说，贝叶斯学习使用数据集D来更新我们对假设h的先验信念，并计算出后验概率P(h|D)，从而找到最佳假设h。

下面就是之前一直提到的对于贝叶斯公式的解释：

Maximum A Posteriori Hypothesis

在许多学习场景中，学习者会考虑一些候选假设的集合H，并且对于给定的观测训练数据D，希望找到其中最有可能成立的假设h，即概率最高的假设。换句话说，贝叶斯学习可以用数据集D来更新我们对每个候选假设的先验信念，并计算出后验概率P(h|D)，从而找到最可能成立的假设h。

候选假设的集合H通常指的是一个假设空间，其中包含了我们可以使用的所有可能的假设。假设空间H的具体形式取决于具体的问题和应用场景，它可以是任何形式的模型或函数空间，例如线性模型、神经网络、支持向量机等等。在贝叶斯学习中，假设空间H中的每个假设都具有一个先验概率，表示我们在看到数据之前对每个假设的初始信念。在观测到数据之后，我们可以使用贝叶斯公式来更新每个假设的后验概率，从而得到最有可能成立的假设。

在贝叶斯学习中，任何概率最大的假设被称为最大后验概率（MAP）假设。

具体地说，对于给定的观测训练数据D和假设空间H，MAP假设h_MAP是使得后验概率P(h|D)最大的假设，即：

h_MAP = argmax P(h|D)=argmax P(D|h)P(h)

其中argmax表示在H中找到使得后面的条件概率最大的假设。

在给定观测数据D和假设空间H的情况下，最大似然假设h_ML是在H中使得P(D|h)最大的假设。也就是说，h_ML是在观测到数据D的情况下，最有可能生成这些数据的假设。

这个例子描述了一个医学诊断问题，涉及到两个可能的假设：

病人患有一种特定类型的癌症（用"cancer"表示）
病人没有癌症（用":cancer"表示）

同时，存在一个实验室检测结果的数据，有两种可能的结果：“positive”（阳性）和"negative"（阴性）。

例子中给出了一些先验概率：
P(cancer) = 0.008 表示患有癌症的先验概率
P(:cancer) = 0.992 表示没有癌症的先验概率
P(positive|cancer) = 0.98 表示在患有癌症的情况下，实验室检测结果为阳性的条件概率
P(negative|cancer) = 0.02 表示在患有癌症的情况下，实验室检测结果为阴性的条件概率
P(positive|:cancer) = 0.03 表示在没有癌症的情况下，实验室检测结果为阳性的条件概率
P(negative|:cancer) = 0.97 表示在没有癌症的情况下，实验室检测结果为阴性的条件概率

现在假设有一个新的病人，实验室检测结果为阳性。问题是：我们应该诊断这个病人是否患有癌症？

根据贝叶斯定理，我们可以计算后验概率来进行诊断：
P(cancer|positive) = P(positive|cancer) * P(cancer) / P(positive)
P(:cancer|positive) = P(positive|:cancer) * P(:cancer) / P(positive)

计算结果如下：
P(cancer|positive) = 0.0078
P(:cancer|positive) = 0.0298

因此，根据最大后验概率（MAP）准则，我们应该诊断这个病人没有癌症（:cancer）。

Does the probability of cancer increase?

根据已知的信息，观察到阳性的实验室测试结果并不一定意味着癌症的可能性增加了。在检测结果为阳性的情况下，患癌的概率(P(cancerl+))实际上是相当低的(0.0078)，这表明检测结果可能是假阳性。在做出诊断之前，考虑其他因素并进行进一步的检查是很重要的。

那这么说的话，只要先验概率足够小，即使检测出来阳性，从统计学上，大概率会被认定为假阳性，那么是不是会出现漏诊的情况。

Yes, that’s correct. When the prior probability of a disease is very low, a positive test result may still be more likely to be a false positive than a true positive. This can result in a high rate of false positives and may lead to misdiagnosis or missed diagnosis. Therefore, it is important to consider multiple factors and conduct additional tests before making a final diagnosis.

那么怎么办呢？
在贝叶斯定理中，我们根据先验概率和似然度来计算后验概率。在这个医疗诊断的例子中，当我们观察到阳性检测结果时，通过贝叶斯定理计算后验概率，我们可以发现患癌症的概率从先验概率0.8%增加到21%，也就是说阳性检测结果提高了患癌症的概率。因此，这段文字的意思是：当我们观察到阳性检测结果时，患癌症的概率会增加。

在这个例子中，我们已经用先验概率0.8%来计算出最初的后验概率，并将其作为新的先验概率。这是因为我们在检测新的患者时，可以将这个先验概率作为我们先前的经验知识，并将其与新的测试结果结合起来，以获得更新的后验概率。这种迭代的过程可以一直进行下去，每次用新的后验概率作为下一次的先验概率，以获得更准确的概率估计。

到这里，好像明白一点了。

Bayes Optimal Classi er

这个问题要求对给定训练数据的新实例进行最可能的分类。给出的示例表明，简单地应用hMAP(最大后验假设)并不总是最好的解决方案。在这个例子中，有三个假设(h1, h2, h3)具有不同的后验概率。hMAP是h1，因为它的后验概率最高。然而，当考虑一个被h1分类为正的、被h2和h3分类为负的新实例时，最可能的分类不一定与hMAP相同。

为了找到最可能的分类，我们需要考虑所有的假设和它们的后验概率。我们可以使用贝叶斯规则来计算给定训练数据的每个假设的后验概率，并使用这些概率来计算新实例被分类为正或负的概率。然后我们可以选择概率最高的分类作为最可能的分类。

贝叶斯分类器需要利用训练数据集得到不同类别的后验概率，并通过这些概率来预测新实例的类别。其中，最有可能的分类是通过将所有假设的预测结果进行加权平均，权重为它们各自的后验概率。这个过程可以通过上面的公式来实现。Bayes optimal classifier的作用是在所有可能分类中找到概率最大的分类。

Example

对于给定的三个假设 h1、h2 和 h3，它们的后验概率分别为 0.4、0.3 和 0.3。如果一个新实例被 h1 分类为正类，被 h2 和 h3 分类为负类，那么可以按照以下步骤计算考虑所有假设后，新实例被分类为正类和负类的概率。

1. 计算新实例被分类为正类的概率：
   P(正类|D) = P(正类|h1)P(h1|D) + P(正类|h2)P(h2|D) + P(正类|h3)P(h3|D)
   = 0.4 * 1 + 0 * P(h2|D) + 0 * P(h3|D) （因为 h1 将新实例分类为正类，所以 P(正类|h1) = 1）
   = 0.4

2. 计算新实例被分类为负类的概率：
   P(负类|D) = P(负类|h1)P(h1|D) + P(负类|h2)P(h2|D) + P(负类|h3)P(h3|D)
   = 0 * P(h1|D) + 0.3 * 1 + 0.3 * 1 （因为 h2 和 h3 将新实例分类为负类，所以 P(负类|h2) = P(负类|h3) = 1）
   = 0.6

因此，考虑所有假设后，新实例被分类为正类的概率为 0.4，被分类为负类的概率为 0.6。这与先前给出的例子一致。注意，这种方式下的分类结果并不等于 hMAP，因为 hMAP 只是单独考虑每个假设的最大后验概率，而不是考虑所有假设的后验概率组合。

Summary

以上面的例子为例，假设我们有三个假设h1、h2、h3，它们的后验概率分别为0.4、0.3和0.3。我们接收到一个新的实例，被h1分类为正类，被h2和h3分类为负类

如果我们只是简单地应用hMAP，则会选择h1作为最有可能的分类器，因为h1的后验概率最高。但是，这并不一定是最好的选择，因为h2和h3的预测也有一定的可信度，不能完全忽略它们的贡献。

相反，我们应该结合所有假设的预测，计算每种预测为正类和负类的概率，然后加权平均得到最终的预测结果。在这个例子中，我们可以发现，考虑所有假设，新实例被分类为正类的概率为0.4，被分类为负类的概率为0.6。因此，我们可以根据这个概率来做出最终的分类决策。

在实际中，上述的假设如何获取

假设通常是通过训练数据集获得的。例如，如果我们要构建一个二元分类器来识别垃圾邮件，我们可以使用已知分类（垃圾邮件和非垃圾邮件）的大量电子邮件作为训练数据集。然后，我们可以使用这些电子邮件中的特征（例如，出现的关键词或短语，邮件主题，发送者等）来训练模型，从而确定每个特征在垃圾邮件和非垃圾邮件中出现的频率，进而获得假设（假设为分类器在不同情况下的分类概率）。然后我们可以使用这些假设来对新的未知邮件进行分类。

再举个例子

假设有一个医学研究项目，需要从医院收集病人的数据，通过这些数据来训练一个模型，以便预测病人是否患有某种疾病。在这个例子中，我们可以假设疾病的发生与否是一个二元分类问题，即每个病人可能被归为患病或不患病的类别中的一个。

我们可以从医院收集一些病人的数据，例如他们的年龄、性别、体重、身高、血压、血糖、家族病史等信息。我们可以将这些信息作为特征，用来训练一个分类器，以便预测每个病人是否患病。

我们可以根据收集到的数据，使用不同的算法或模型来训练分类器，例如决策树、逻辑回归、支持向量机等。在训练分类器时，我们可以使用交叉验证等技术来选择最好的模型和参数，以提高分类器的准确性。

最终，我们可以根据训练好的模型来预测新的病人是否患有该疾病。当我们有新的病人数据时，我们可以将这些数据输入到模型中，模型将根据学习到的知识来预测该病人是否患病，并给出相应的后验概率。

可以理解上述的三个假设是特征所预测结果的概率吗

不完全正确。在这个例子中，假设 $h_1$, $h_2$ 和 $h_3$ 代表了不同的分类器，它们对于同一个输入会得到不同的预测结果。在这里，我们假设每个分类器的预测结果是二元的（正类或负类），而 $h_1$, $h_2$ 和 $h_3$ 的后验概率分别表示给定训练数据后，这些分类器的准确性。因此，这些后验概率并不是特征预测结果的概率，而是表示每个分类器的可信程度。

在实际情况中，我们可以使用不同的特征和算法来构建分类器，然后根据训练数据对每个分类器进行评估，计算出它们的后验概率。例如，在图像分类任务中，我们可以使用不同的图像特征提取方法和分类算法来构建多个分类器，然后通过对训练图像的分类结果进行评估，计算出每个分类器的后验概率。然后，我们可以将这些分类器的预测结果组合起来，得到最终的分类结果。

贝叶斯策略也是一种集成学习

是的，可以这样理解。贝叶斯策略的核心思想是综合不同假设的预测结果，通过后验概率来对假设的可信度进行加权，得到最终的预测结果。在这个过程中，不同的假设可以看作是不同的“模型”，而后验概率则对应了每个模型的“权重”，因此贝叶斯策略可以被看作是一种集成学习的方法。不同之处在于，贝叶斯策略的权重是由数据决定的，而不是通过学习算法得到的。

解释：不同之处在于，贝叶斯策略的权重是由数据决定的，而不是通过学习算法得到的。

在贝叶斯策略中，假设的后验概率是通过先验概率和数据的似然函数相乘得到的，而先验概率是在没有数据的情况下给出的，代表了我们对假设的先前信念。然后，当有新数据出现时，我们通过贝叶斯公式来计算假设的后验概率，这里的数据会影响我们对假设的信念，进而影响权重的计算。因此，权重是由数据决定的，而不是由学习算法得到的。与集成学习中的权重可能是由学习算法得出的不同。

Averaging的权重是由算法得到的

Averaging的权重是由算法得到的。在Averaging中，每个模型的预测结果被简单平均，每个模型对于最终结果的贡献是相等的。而这些模型的权重是通过训练算法来确定的，例如通过交叉验证、正则化等方法来确定每个模型的权重。因此，Averaging的权重是由算法得到的，而不是由数据得到的。