本文介绍了通过《Think Python》书中练习4-4，学习如何设计一个使用基本元素绘制大写英文字母的系统。作者强调了编程中结构化思维的重要性，如用完乌龟（绘图工具）要归位，以及模块化设计，确保各部分相互独立。在实践中，作者经历了字体设计、元素抽象和代码实现的过程，最终实现了包含直线、斜线和弧线的26个大写字母绘制函数。
第4章 案例研究：接口设计
练习 4-4 用函数画大写字母表
字母表中的字母可以使用一些基本元素来构成，如横线、竖线以及一些曲线。设计一个字母表，可以使用最少的基本元素画出来，并且编写函数来画出字母。
【求解】
这道题教会我最重要的一件事是：用完东西要放回原处。
虽然这么简单的一个道理，父母从小就教，但是我根本没care，常用的东西放在显眼的地方，不常用的东西就随缘了，到用的时候再找。
平时生活中用东西我都当成了一个件独立的事，并没有连成整体思考，但是通过本题 打字机代码 验证的时候把26个字母连成了整体，我第一次验证的时候，虽然能打出字，但是不仅对不齐，甚至有的字母还是躺着的……就是因为画完每个字母乌龟没有归位，后面又花了时间重新给每个字母乌龟用前移动到起点、用完归位。
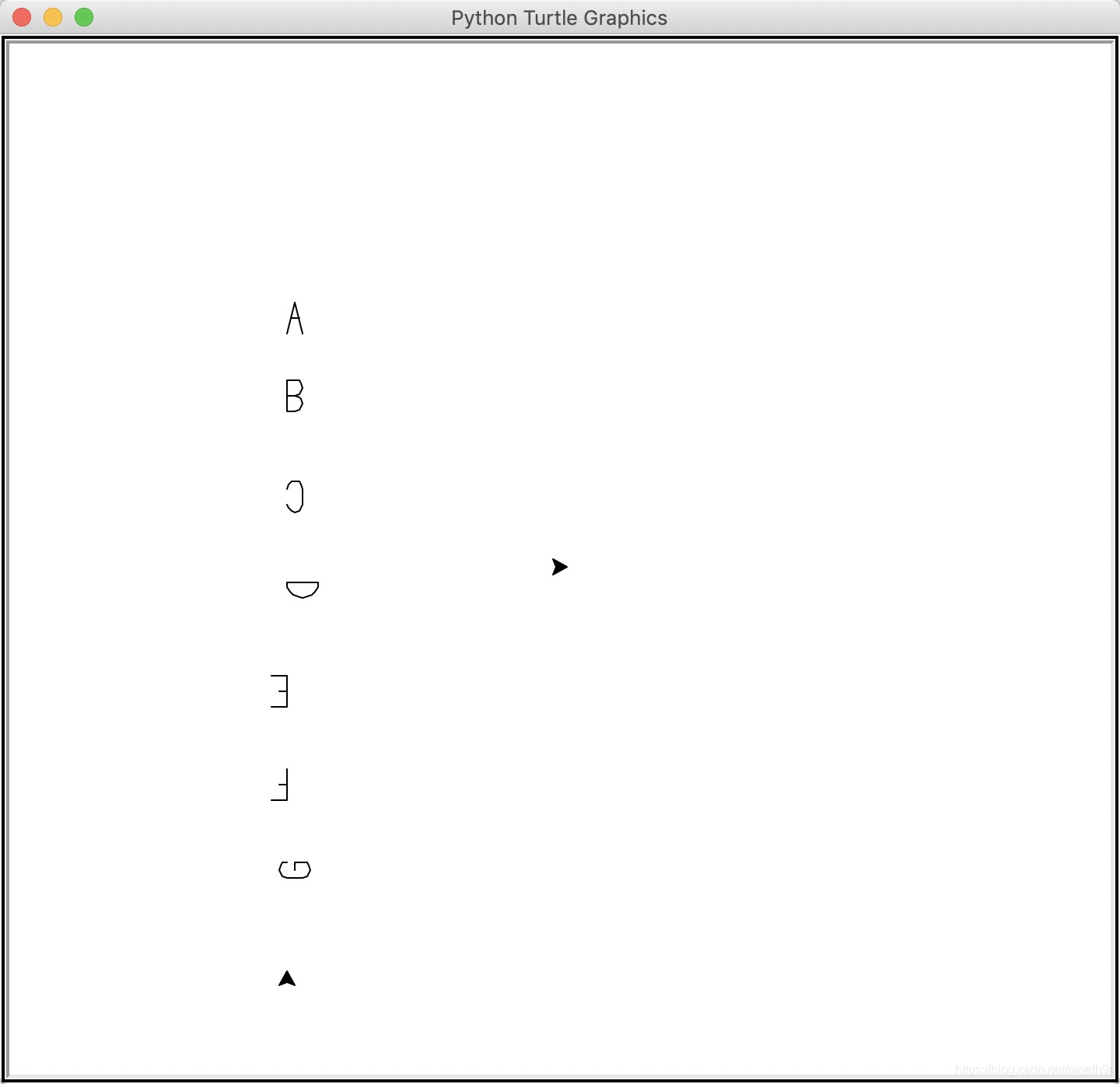
第二个道理是：将应用模块与公共调用模块彻底分开。
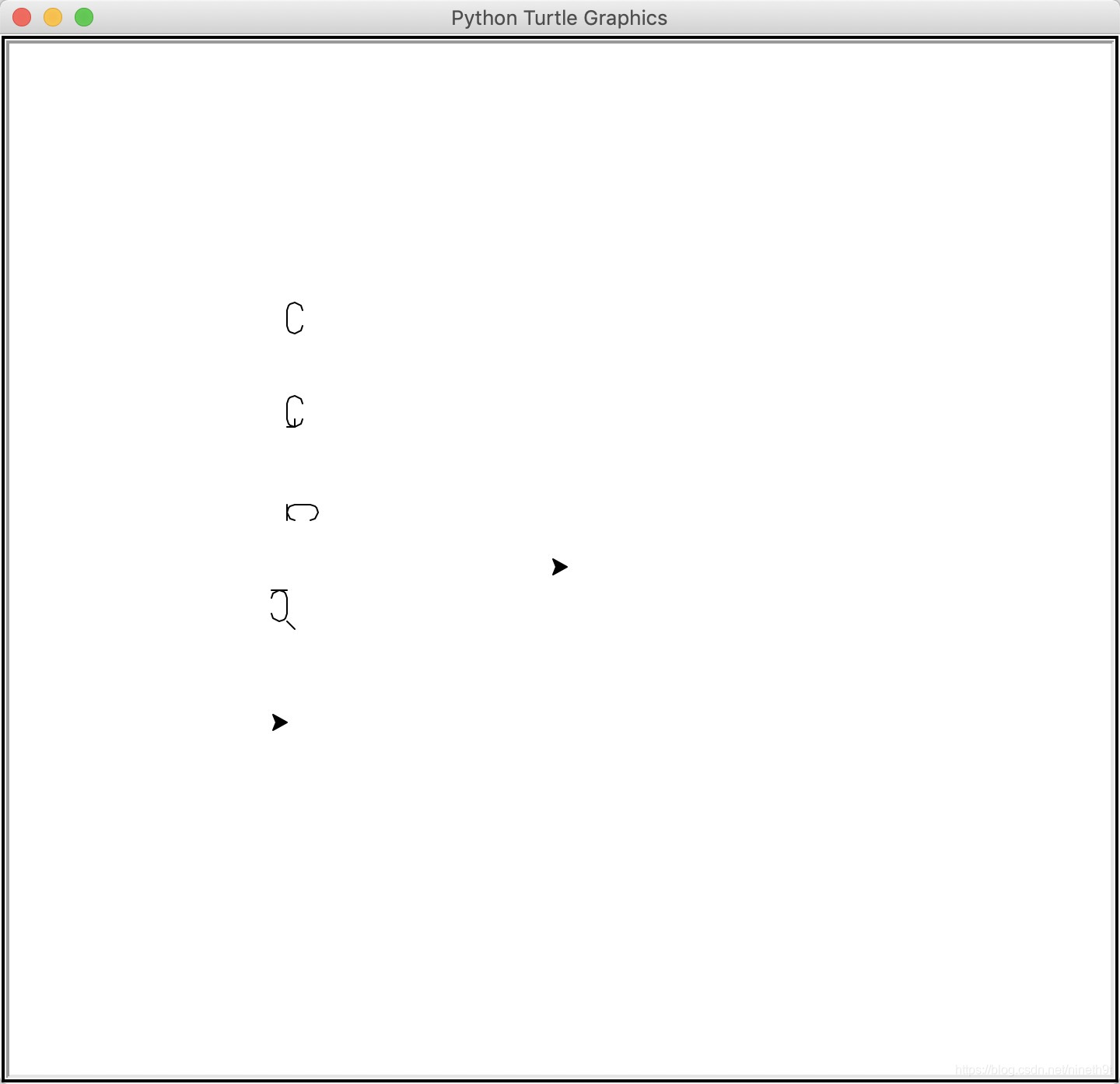
由于验证的时候发生了“没有归位”的问题，当时就想赶紧归位解决了，在每个字母的函数后面直接添加归位位移，结果在验证有的字母就直接变形了。
比如我的G、O、Q是在画完没有归位的C的基础上直接添加直角、竖线、斜线完成的，G、O直接调的C，Q直接调的O，当我给C的乌龟归位后，调用C的这3个字母的其他部分全都跟着位移了……导致后面很多字母都重写了（不仅这几个字母，还有很多直线我之前直接用的draw_i）。
Step.1 设计字体
本来想设计一个像电子表数字的字体，丑点就丑点不要画弧线（弧线麻烦），但是发现26个字母，形态还是挺丰富的，光靠直线不行必须要弧线……
话说这题其实是锻炼抽象能力吧？草稿改了两次，终于统一到只保留横线、竖线、左斜线、右斜线、弧线：
这里N写错了不要在意，后面调试的时候发现改过来了（虽然是在写这篇文章的时候）
Step.2 分类抽象
横竖线：E、F、H、I、L、T
左右斜线：A、K、M、N、V、W、X、Y、Z
半圆+横线：B、P、R
半圆+竖线：J、U
基于C：C、G、O、Q
只有弧线：S
Step.3 问题求解
只有弧线：S
#多边线
def polyline(t, n, length, angle):
for i in range(n):
t.fd(length)
t.lt(angle)
#弧
def arc(t, r, angle):
arc_length = 2 * math.pi * r * abs(angle) / 360
n = int(arc_length / 4) + 3
step_length = arc_length / n
step_angle = float(angle) / n
t.lt(step_angle/2)
polyline(t, n, step_length, step_angle)
t.rt(step_angle/2)
横竖线：E、F、H、I、L、T
#线段
def line(t, l):
t.fd(l)
#左转直角
def right_angle(t, l1, l2):
line(t, l1)
t.lt(90)
line(t, l2)
左右斜线：A、K、M、N、V、W、X、Y、Z
#左斜线
def l_slash(t, tan, l):
angle = math.atan(tan) * 180 / math.pi
m = math.sqrt( 1 / tan**2 + 1) * l
t.lt(angle)
line(t, m)
t.rt(angle)
#右斜线
def r_slash(t, tan, l):
angle = math.atan(tan) * 180 / math.pi
m = math.sqrt( 1 / tan**2 + 1) * l
t.rt(angle)
line(t, m)
t.lt(angle)
半圆+横线：B、P、R
#B、P、R公共部分：
def bpr(t, l):
r = l/4
angle = 180
line(t, r)
arc(t, r, angle)
line(t, r)
基于C：C、G、O、Q
#C、G、O、Q公共部分：
def cgoq(t, l):
#移动到起点
t.pu()
right_angle(t, l*1/2, l*3/4)
t.pd()
#C
arc(t, l/4, 180)
line(t, l/2)
arc(t, l/4, 180)
Step.4 完成代码
文件 letters.py 中不要有具体函数的调用指令，要不然你还没打字，typewriter.py 就直接执行这个函数了。也不要有 turtle.mainloop() 指令，要不然还没开始就什么都执行不了。
"""
《Think Python》练习 4-4：字母表
基本元素：弧线、直线、左斜线、右斜线
"""
#引入数学模块、乌龟模块
import math
import turtle
#调用乌龟画图、提高画弧速度
bob = turtle.Turtle()
bob.delya = 0.01
#多边线
def polyline(t, n, length, angle):
for i in range(n):
t.fd(length)
t.lt(angle)
#弧
def arc(t, r, angle):
arc_length = 2 * math.pi * r * abs(angle) / 360
n = int(arc_length / 4) + 3
step_length = arc_length / n
step_angle = float(angle) / n
t.lt(step_angle/2)
polyline(t, n, step_length, step_angle)
t.rt(step_angle/2)
#线段
def line(t, l):
t.fd(l)
#左转直角
def right_angle(t, l1, l2):
line(t, l1)
t.lt(90)
line(t, l2)
#左斜线
def l_slash(t, tan, l):
angle = math.atan(tan) * 180 / math.pi
m = math.sqrt( 1 / tan**2 + 1) * l
t.lt(angle)
line(t, m)
t.rt(angle)
#右斜线
def r_slash(t, tan, l):
angle = math.atan(tan) * 180 / math.pi
m = math.sqrt( 1 / tan**2 + 1) * l
t.rt(angle)
line(t, m)
t.lt(angle)
#B、P、R公共部分：
def bpr(t, l):
r = l/4
angle = 180
line(t, r)
arc(t, r, angle)
line(t, r)
#C、G、O、Q公共部分：
def cgoq(t, l):
#移动到起点
t.pu()
right_angle(t, l*1/2, l*3/4)
t.pd()
#C
arc(t, l/4, 180)
line(t, l/2)
arc(t, l/4, 180)
#A
def draw_a(t, l):
l_slash(t, 4, l)
r_slash(t, 4, l)
#A中的横线
t.pu()
t.lt(90)
right_angle(t, l/2, l*3/8)
t.lt(180)
t.pd()
line(t, l/4)
#归位
t.pu()
t.lt(180)
right_angle(t, l*3/8, l/2)
t.lt(90)
#B
def draw_b(t, l):
bpr(t, l)
t.lt(180)
bpr(t, l)
t.lt(90)
line(t, l)
#归位
t.lt(90)
#C
def draw_c(t, l):
#画C
cgoq(t,l)
#归位
t.pu()
t.lt(90)
right_angle(t, l*1/2, l*1/4)
t.lt(90)
#D
def draw_d(t,l):
arc(t, l/2, 180)
t.lt(90)
line(t, l)
#归位
t.lt(90)
#E
def draw_e(t, l):
#F
draw_f(t, l)
#线
line(t, l/2)
#归位
t.pu()
t.lt(180)
line(t, l/2)
t.lt(180)
#F
def draw_f(t, l):
#移动到起点
t.pu()
right_angle(t, l/2, l)
t.pd()
#直角
t.lt(90)
right_angle(t, l/2, l/2)
#线
t.lt(90)
line(t, l/4)
#直角
t.lt(180)
right_angle(t, l/4, l/2)
#归位
t.lt(90)
#G
def draw_g(t, l):
#画C
cgoq(t, l)
#补G
right_angle(t, l/4, l/4)
#归位
t.pu()
right_angle(t, l/4, l/2)
t.lt(90)
#H
def draw_h(t, l):
t.lt(90)
line(t, l)
t.pu()
t.rt(90)
line(t, l/2)
t.rt(90)
t.pd()
line(t, l)
t.lt(180)
right_angle(t, l/2, l/2)
#归位
t.pu()
t.lt(90)
line(t, l/2)
t.lt(90)
#I
def draw_i(t, l):
#移动到起点
t.pu()
line(t, l/4)
t.lt(90)
#画I
t.pd()
line(t, l)
#归位
t.pu()
t.lt(90)
right_angle(t, l/4, l)
t.lt(90)
#J
def draw_j(t, l):
#移动到起点
t.pu()
t.lt(90)
line(t, l/4)
t.lt(180)
#画J
t.pd()
arc(t, l/4, 180)
line(t, l*3/4)
#归位
t.pu()
t.lt(90)
right_angle(t, l/2, l)
t.lt(90)
#K
def draw_k(t, l):
#计算斜边长度
m = l * math.sqrt(2) / 2
#画K
t.lt(90)
line(t, l)
t.pu()
t.rt(90)
line(t, l/2)
t.rt(135)
t.pd()
right_angle(t, m, m)
#归位
t.pu()
t.rt(135)
line(t, l/2)
t.lt(180)
#L
def draw_l(t, l):
#移动到起点
t.pu()
t.lt(90)
line(t, l)
t.lt(180)
#画L
t.pd()
right_angle(t, l, l/2)
#归位
t.pu()
t.lt(180)
line(t, l/2)
t.lt(180)
#M
def draw_m(t, l):
t.lt(90)
line(t, l)
t.rt(90)
r_slash(t, 2, l/2)
l_slash(t, 2, l/2)
t.rt(90)
line(t, l)
#归位
t.pu()
t.rt(90)
line(t, l/2)
t.lt(180)
#N
def draw_n(t, l):
#移动到起点
t.pu()
t.lt(90)
line(t, l)
t.lt(180)
#画N
t.pd()
line(t, l)
t.lt(90)
l_slash(t, 2, l)
t.rt(90)
line(t, l)
#归位
t.pu()
t.rt(90)
line(t, l/2)
t.lt(180)
#O
def draw_o(t, l):
cgoq(t, l)
line(t, l/2)
#归位
t.pu()
t.lt(90)
right_angle(t, l/2, l*3/4)
t.lt(90)
#P
def draw_p(t, l):
#移动到起点
t.pu()
t.lt(90)
line(t, l/2)
t.rt(90)
#画P
t.pd()
bpr(t, l)
t.lt(90)
line(t, l)
#归位
t.lt(90)
#Q
def draw_q(t, l):
#画O
cgoq(t, l)
line(t, l/2)
#画丶
t.pu()
t.lt(90)
right_angle(t, l/4, l/2)
t.lt(90)
t.pd()
r_slash(t, 1, l/4)
#归位
t.pu()
t.lt(180)
line(t, l/2)
t.lt(180)
#R
def draw_r(t, l):
#移动到起点
t.pu()
t.lt(90)
line(t, l/2)
t.rt(90)
#画P
t.pd()
bpr(t, l)
t.lt(90)
line(t, l)
#画丶
t.lt(180)
line(t, l/2)
t.rt(90)
r_slash(t, 1, l/2)
#归位
t.pu()
t.lt(180)
line(t, l/2)
t.lt(180)
#S
def draw_s(t, l):
#移动到起点
t.pu()
right_angle(t, l/2, l*3/4)
#画270°弧
t.pd()
arc(t, l/4, 270)
t.pu()
t.lt(180)
right_angle(t, l/4, l/4)
t.pd()
arc(t, l/4, 270)
#归位
t.pu()
right_angle(t, l/4, l/2)
t.lt(90)
#T
def draw_t(t, l):
#移动到起点
t.pu()
t.lt(90)
line(t, l)
t.rt(90)
#画T
t.pd()
line(t, l/2)
t.lt(180)
right_angle(t, l/4, l)
#归位
t.pu()
t.rt(90)
line(t, l/4)
t.lt(180)
#U
def draw_u(t, l):
#移动到起点
t.pu()
t.lt(90)
line(t, l)
t.lt(180)
#画U
t.pd()
line(t, l*3/4)
arc(t, l/4, 180)
line(t, l*3/4)
#归位
t.pu()
t.lt(90)
right_angle(t, l/2, l)
t.lt(90)
#V
def draw_v(t, l):
#移动到起点
t.pu()
t.lt(90)
line(t, l)
t.rt(90)
#画V
t.pd()
r_slash(t, 4, l)
l_slash(t, 4, l)
#归位
t.pu()
t.lt(180)
right_angle(t, l/2, l)
t.lt(90)
#W
def draw_w(t, l):
#移动到起点
t.pu()
right_angle(t, l/2, l)
t.lt(180)
#画W
t.pd()
line(t, l)
t.rt(90)
r_slash(t, 2, l/2)
l_slash(t, 2, l/2)
t.rt(90)
line(t, l)
#归位
t.pu()
t.lt(180)
line(t, l)
t.lt(90)
#X
def draw_x(t, l):
#移动到起点
t.pu()
t.lt(90)
line(t, l)
t.rt(90)
#画X
t.pd()
r_slash(t, 2, l)
t.pu()
line(t, -l/2)
t.pd()
l_slash(t, 2, l)
#归位
t.pu()
t.lt(180)
right_angle(t, l/2, l)
t.lt(90)
#Y
def draw_y(t, l):
#移动到起点
t.pu()
t.lt(90)
line(t, l)
t.rt(90)
#画Y
t.pd()
r_slash(t, 1, l/4)
l_slash(t, 1, l/4)
t.pu()
t.lt(180)
right_angle(t, l/4, l/4)
t.pd()
line(t, l/2)
#归位
t.pu()
t.rt(90)
line(t, l/4)
t.lt(180)
#Z
def draw_z(t, l):
#移动到起点
line(t, l/2)
#画Z
t.lt(180)
line(t, l/2)
t.rt(180)
l_slash(t, 2, l)
t.lt(180)
line(t, l/2)
#归位
t.pu()
t.lt(90)
line(t, l)
t.lt(90)
扫一扫
4320
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
