【程序分享】Warren Cowley Parameters 程序：表征短程有序的化学基序

最新推荐文章于 2025-04-02 18:44:50 发布

123wxw

最新推荐文章于 2025-04-02 18:44:50 发布

阅读量1.3k

点赞数 22

文章标签：分子动力学 LAMMPS 第一性原理计算原子结构力学性质

本文链接：https://blog.csdn.net/nmrwxw/article/details/142213453

版权

================================

分享一个 Warren Cowley Parameters 程序：表征短程有序的化学基序。

感谢论文的原作者！

================================

主要内容

“晶体材料的化学成分具有原子尺度的波动，可调节各种中尺度特性。建立此类材料的化学-微结构关系需要对这些化学波动进行适当的表征。然而，目前的表征方法（如 Warren-Cowley 参数）只能部分利用局部化学图案所包含的完整化学和结构信息。在此，我们介绍一种基于 E(3)- 等变图神经网络的框架，它能够完全识别任意化学元素数量的任意晶体结构中的化学图案。这种方法自然而然地为量化化学复杂材料中的化学短程有序（SRO）提供了一种适当的信息论度量，并为化学空间提供了一种精简但完整的表征。我们的框架可以将任何原子间性质与其相应的局部化学主题相关联，从而为探索化学复杂材料的结构-性质关系提供了新的途径。我们使用 MoTaNbTi 高熵合金作为测试系统，通过评估与每个化学主题相关的晶格应变，以及计算化学波动长度尺度的温度依赖性，展示了这种方法的多功能性。”——取自文章摘要。

================================

Figure 1

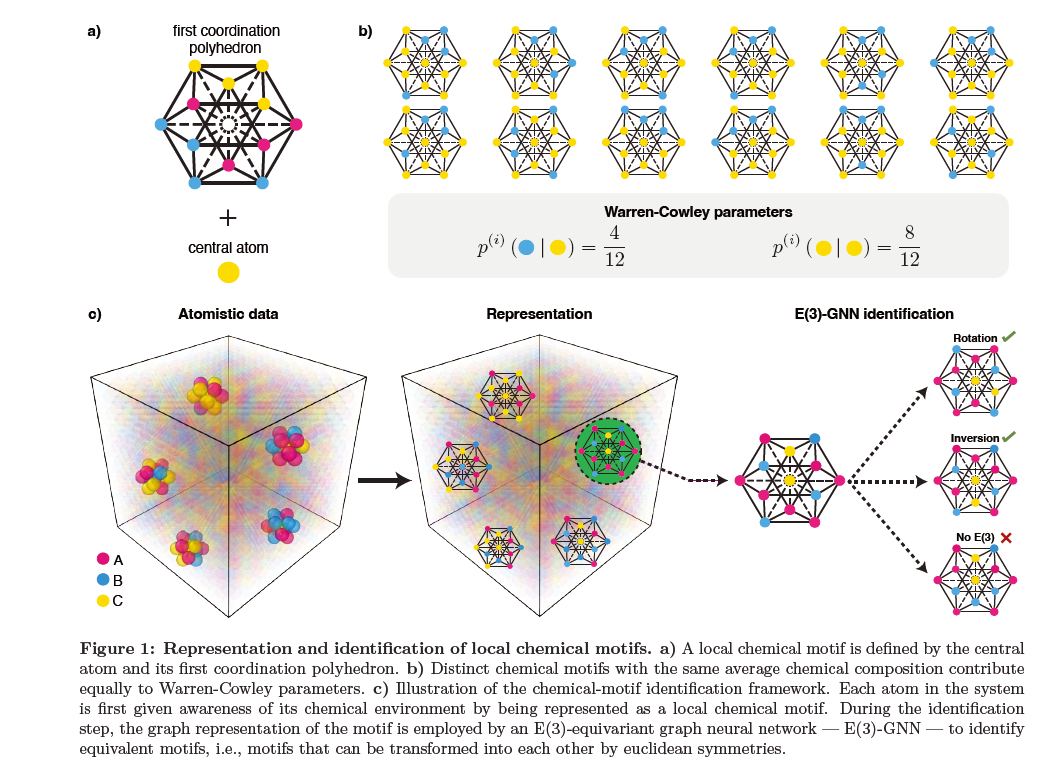
Figure 2

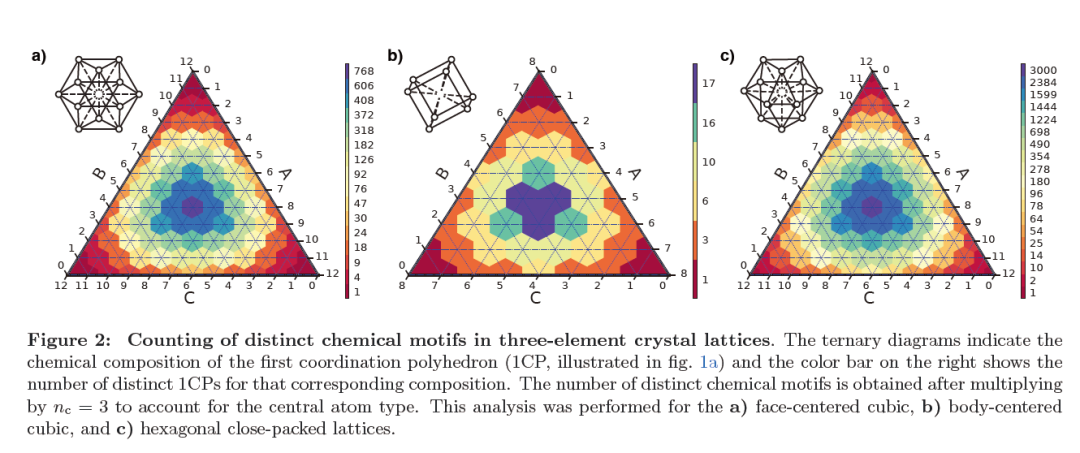
Figure 3

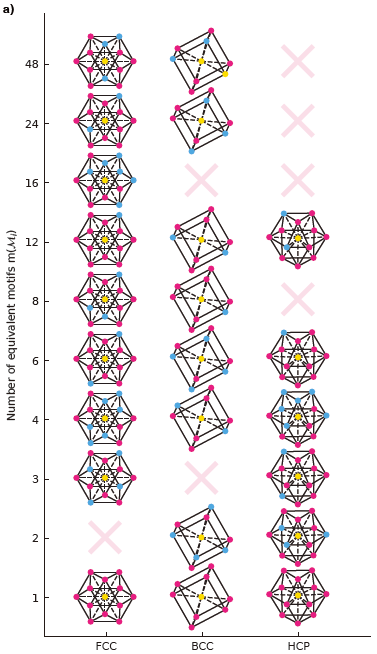
Figure 4

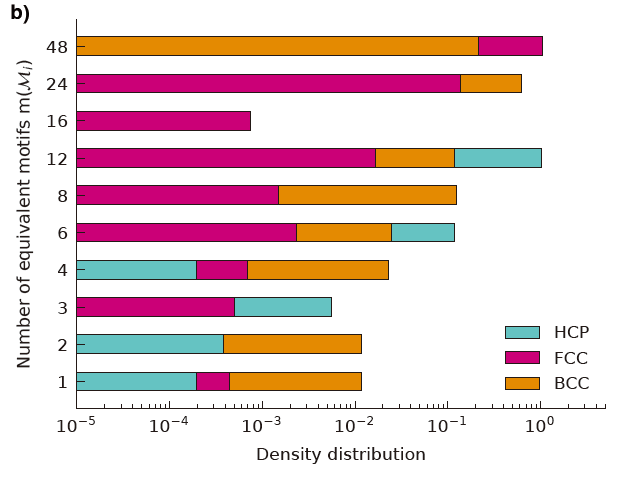
Figure 5

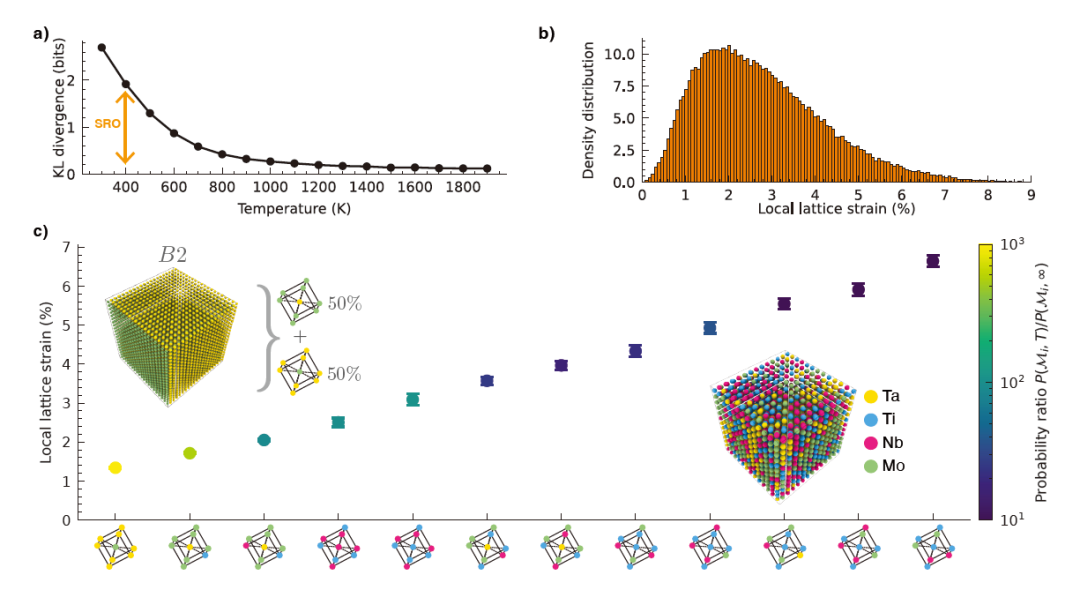
Figure 6

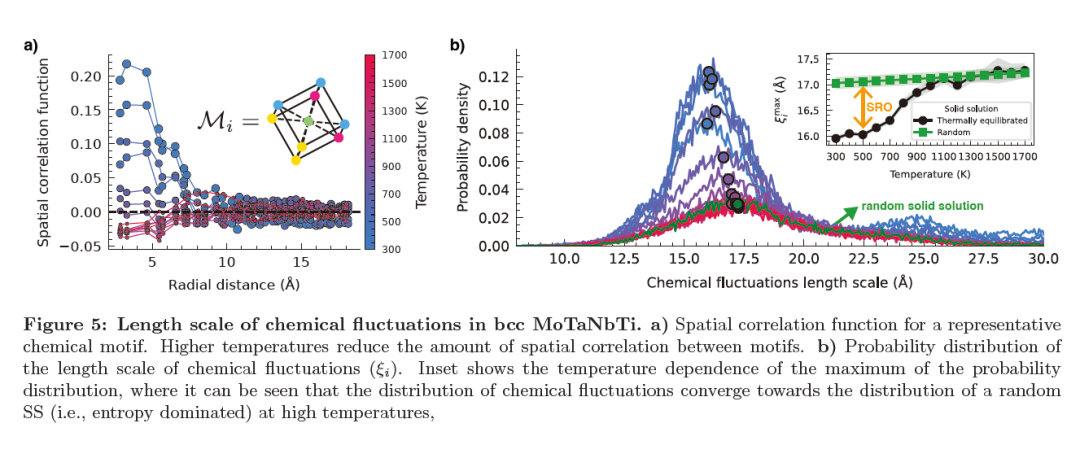
Figure 7

WarrenCowleyParameters

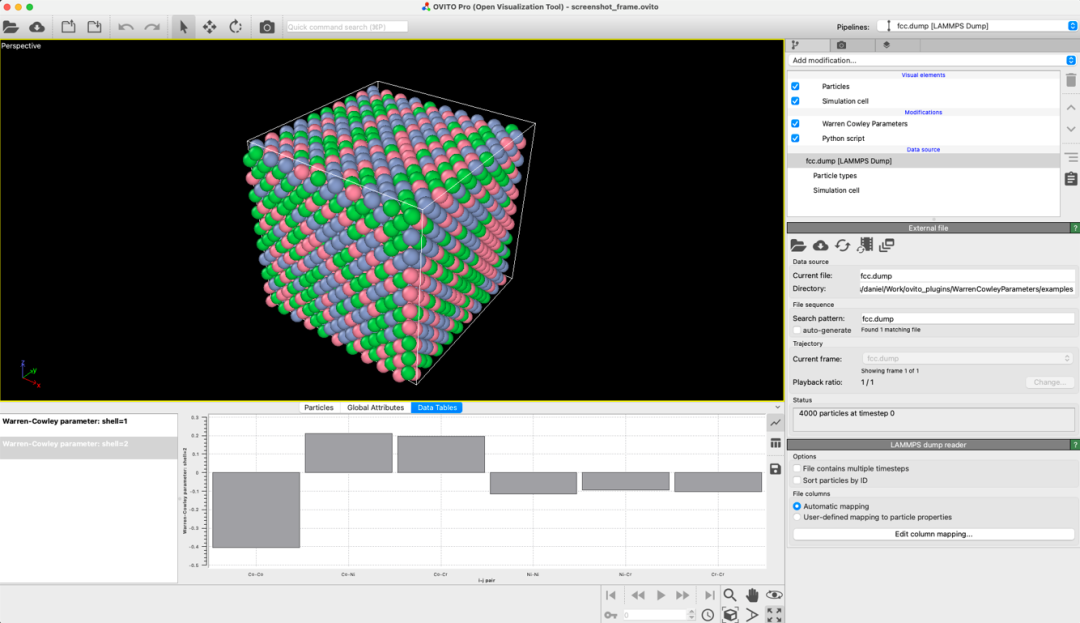
OVITO Python modifier to compute the Warren-Cowley parameters, defined as:

α i j m = 1 − p i j m c j ,

where m denotes the m-th nearest-neighbor shell, p i j m is the average probability of finding a j-type atom around an i-type atom in the m-th shell, and c j is the average concentration of j-type atom in the system. A negative α i j m suggests the tendency of j-type clustering in the m-th shell of an i-type atom, while a positive value means repulsion.

from ovito.io import import_fileimport WarrenCowleyParameters as wc
pipeline = import_file("fcc.dump")mod = wc.WarrenCowleyParameters(nneigh=[0, 12, 18], only_selected=False)pipeline.modifiers.append(mod)data = pipeline.compute()
wc_for_shells = data.attributes["Warren-Cowley parameters"]print(f"1NN Warren-Cowley parameters: \n {wc_for_shells[0]}")print(f"2NN Warren-Cowley parameters: \n {wc_for_shells[1]}")

Installation

For a standalone Python package or Conda environment, please use:

pip install --user WarrenCowleyParameters

For OVITO PRO built-in Python interpreter, please use:

ovitos -m pip install --user WarrenCowleyParameters

If you want to install the lastest git commit, please replace WarrenCowleyParameters by git+https://github.com/killiansheriff/WarrenCowleyParameters.git.