基于matlab解释统计插值系统方法

插值是一种用于在已知数据点之间估计未知数据点的值的数学方法，常用于数据分析和预测。

插值的意义：

1. 数据完整性：在数据缺失的情况下，插值可以帮助我们填补数据空白，使数据集更加完整。
2. 预测：插值可以用来预测未来的趋势或估计过去未记录的值。
3. 平滑处理：插值可以用于平滑数据，去除噪声，使数据更加易于分析。

1. 线性插值 (Linear Interpolation)

   线性插值中的“线性”指的是在两个已知数据点之间进行插值时，使用一条直线（线性函数）来近似这两个点之间的变化。这种插值方法假设数据在两个已知点之间变化是均匀的，即变化率是恒定的。线性插值通常用于以下情况：

   • 一维数据：当你有两个已知的数据点 (x1,y1) 和 (x2​,y2​)，并且需要找到一个点 (x,y)，其中 x1<x<x2​，线性插值会通过这两个点画一条直线，并找到这条直线上与 x 相匹配的 y 值。

   • 公式：线性插值的公式可以表示为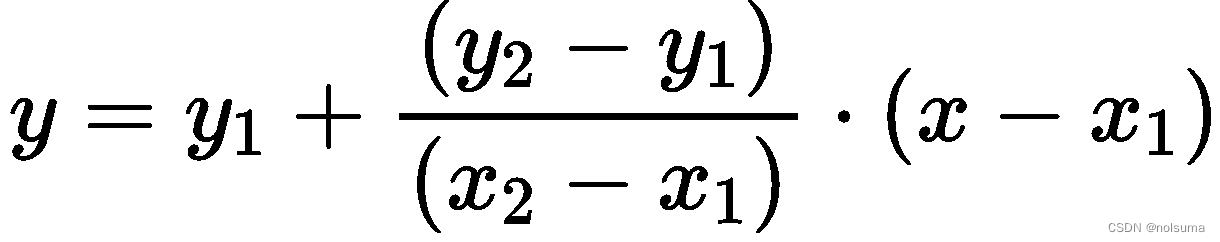： 这个公式计算了从y1 到 y2的变化量，并根据 x 的位置并按比例分配。

   • 使用matlab示例正弦波数据集，从中选择一些点作为已知数据点。定义新的x值集合，并使用interp1函数进行了线性插值。

   % 定义数据的x和y值
   x = linspace(0, 2*pi, 100); % 生成100个点在0到2*pi之间
   y = sin(x); % y是x的正弦函数
   
   % 选择一些数据点进行插值
   x_known = [0, pi/2, pi, 3*pi/2, 2*pi];
   y_known = sin(x_known);
   
   % 定义需要进行插值的x值
   x_new = linspace(0, 2*pi, 1000); % 在整个区间内生成1000个点
   
   % 使用线性插值
   y_new = interp1(x_known, y_known, x_new, 'linear', 'extrap');
   
   % 绘制原始数据点和插值后的数据
   figure;
   plot(x, y, 'b-', 'LineWidth', 2); % 原始数据
   hold on;
   plot(x_known, y_known, 'ro', 'MarkerFaceColor', 'r'); % 已知数据点
   plot(x_new, y_new, 'g-', 'LineWidth', 1); % 插值后的数据
   legend('Original Data', 'Known Data Points', 'Interpolated Data');
   title('Linear Interpolation');
   xlabel('x');
   ylabel('y');
   grid on;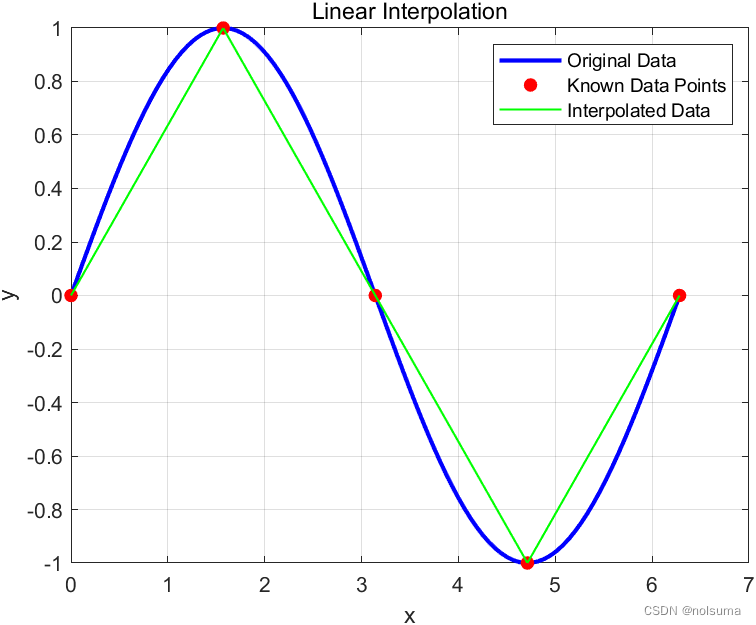

   通过使用关键的interp1函数进行了线性插值

   y_new = interp1(x_known, y_known, x_new, 'linear', 'extrap');

   x_known 是已知数据点的x坐标。

   y_known 是与 x_known 对应的y坐标。

   x_new 是需要进行插值的新的x坐标点。

   'linear' 指定了插值方法为线性插值。

   'extrap' 指定了外推方法，这里 'extrap' 是一个保留字，表示当 x_new 中的点超出了 x_known 的范围时，MATLAB将使用最近的数据点进行线性外推。

2. 多项式插值 (Polynomial Interpolation)

   1.拉格朗日插值。
   
   
   拉格朗日插值定理假设我们有一组数据点 (x0,y0),(x1,y1),…,(xn,yn)，拉格朗日插值的目标是找到一个n次多项式 P(x)，使得对于所有的i（i=0,1,…,n），都有 P(xi)=yi。

%% 使用正弦函数和余弦函数的组合来创建数一个复杂的数据集：

% 创建复杂的数据集
x = linspace(0, 2*pi, 10); % 生成10个数据点
y = sin(x) + cos(x);

% 绘制原始数据点
figure;
plot(x, y, 'o', 'MarkerFaceColor', 'r');
hold on;
grid on;
title('Original Data Points');
xlabel('x');
ylabel('y');

%% 编写一个拉格朗日插值的函数：

function y_interp = lagrange_interpolation(x, y, x_interp)
    n = length(x);
    y_interp = zeros(size(x_interp));
    for i = 1:length(x_interp)
        for j = 1:n
            L = 1;
            for k = 1:n
                if k ~= j
                    L = L * (x_interp(i) - x(k)) / (x(j) - x(k));
                end
            end
            y_interp(i) = y_interp(i) + L * y(j);
        end
    end
end

%% 函数接受三个参数：已知数据点的x坐标 x，对应的y坐标 y，以及需要进行插值的x坐标 x_interp。它返回插值后的y坐标 y_interp后使用这个函数进行拉格朗日插值，并绘制插值结果：

% 定义插值点
x_interp = linspace(0, 2*pi, 100);

% 进行拉格朗日插值
y_interp = lagrange_interpolation(x, y, x_interp);

% 绘制插值结果
plot(x_interp, y_interp, 'b-', 'LineWidth', 2);
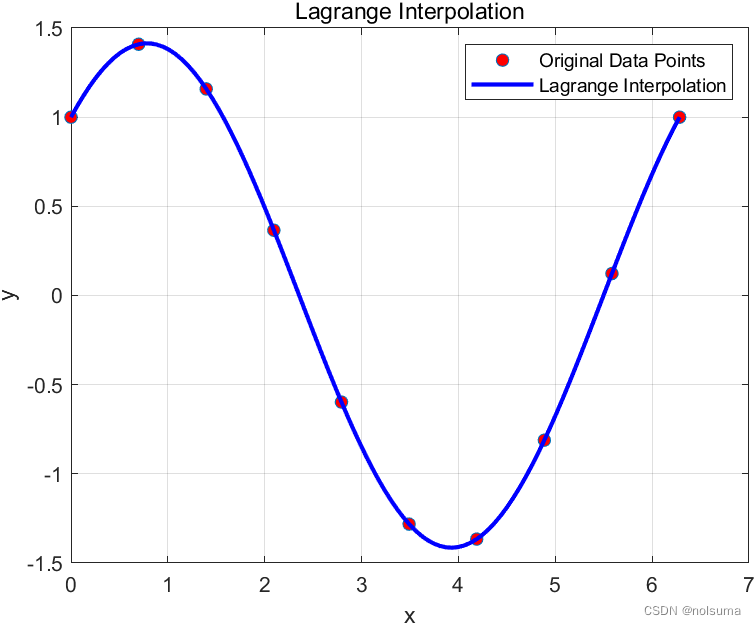
legend('Original Data Points', 'Lagrange Interpolation');
title('Lagrange Interpolation');
xlabel('x');
ylabel('y');

关键讲解：

在最内层循环：(for k = 1:n):这个循环也是遍历所有的已知数据点，构建拉格朗日基多项式 L_j(x)。对于每个 j，我们计算基多项式 L 的一个因子，这个因子是通过对 x_interp(i) 和所有其他已知点 x(k) 的差值进行线性组合得到：

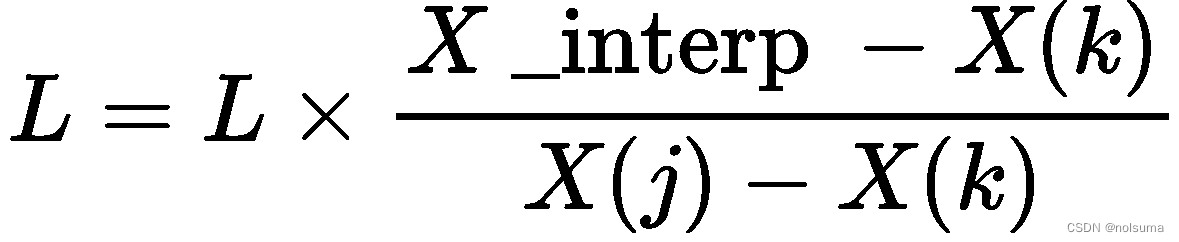
for k = 1:n：k依次取值1到n，其中x = linspace(0, 2*pi, 10);，n = length(x);即从0到2Π的十个间隔点。if k ~= j: 这个条件确保我们不会因为分母为零而产生除以零的错误。

次外层循环：循环遍历所有的已知数据点 (x(j), y(j))。对于每个已知点，我们计算与 x_interp(i) 相关的拉格朗日基多项式 L_j(x) 的值。

最外层循环：(for i = 1:length(x_interp)): 这个循环遍历所有需要进行插值的点 x_interp。对于每个 x_interp(i)，我们计算相应的插值结果 y_interp(i)。

2.牛顿插值（Newton Interpolation）

通过构建一个差分数列来构造插值多项式。增加新的数据点时，不需要重新计算整个多项式，只需要添加一个新的项。牛顿插值的基本思想是，对于一组给定的数据点 (x0,y0),(x1,y1),…,(xn,yn)我们可以构造一个n次多项式 Pn(x)，使得 Pn(xi)=yi 对所有的i=0,1,…,n都成立。


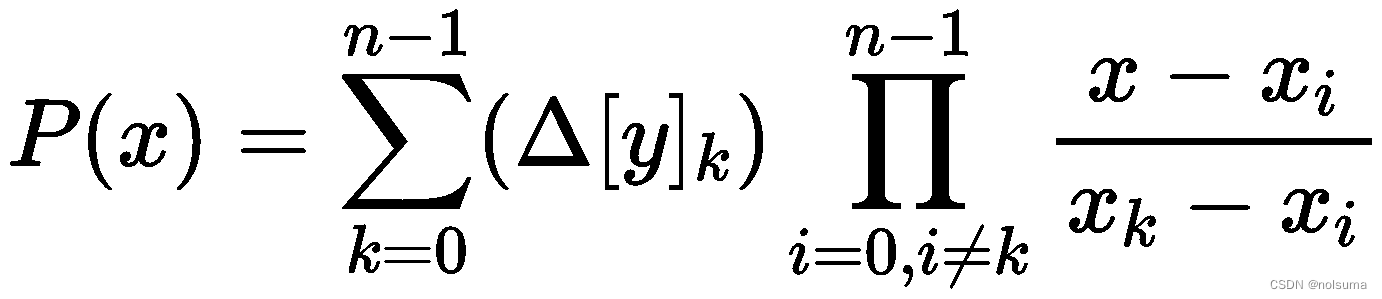
使用牛顿插值遵循以下步骤

1. 步骤 1: 收集数据点
   首先，你需要一组数据点 (x0,y0),(x1,y1),…,(xn,yn)这些数据点是你想要通过插值多项式来近似的。

2. 步骤 2: 构建差分表
   使用这些数据点，构建一个差分表。差分表是一个 n+1 阶的方阵，其中包含了原始 𝑦 值的各阶差分。
   初始化一个 (𝑛n1)×(n+1) 的矩阵 dd_table，填充为0。
   将 𝑦y 值复制到 dd_table 的第一列。
   使用嵌套循环计算 dd_table的每个元素，根据差分的定义：
   
   其中 i 从1到 n，j从2到 n+1。

3. 步骤 3: 从差分表中提取系数
   牛顿插值多项式的系数是差分表的第一列元素，即 y0,Δy0,Δ2y0,…,Δny0，其中 Δky0Δky0​ 是 y0的 𝑘阶差分。

4. 步骤 4: 定义插值多项式
   牛顿插值多项式 P(x)可以递归地定义为： P(x)=y0+(x−x0)⋅Δy0+(x−x0)(x−x1)⋅Δ2y0+…+(x−x0)(x−x1)…(x−xn−1)⋅Δny0​ 这里的每一项都是差分表中的一个系数乘以 x 的一个多项式。

% 步骤 1: 收集数据点
x = linspace(0, 2*pi, 5); % 示例数据点
y = sin(x);

% 步骤 2: 构建差分表
dd_table = zeros(length(x), length(x));
dd_table(:, 1) = y;
for j = 2:1:length(x)
    for i = 1:(length(x) - j + 1)
        dd_table(i,j) = (dd_table(i+1,j-1) - dd_table(i,j-1)) / (x(i+j-1) - x(i));
    end
end

% 步骤 3: 从差分表中提取系数
coefficients = dd_table(1, :);

% 定义牛顿插值多项式函数
function P = newton_interp(x, coefficients, x_query)
    P = zeros(size(x_query));
    for i = 1:length(x_query)
        P(i) = coefficients(1);
        for j = 2:length(coefficients)
            P(i) = P(i) + coefficients(j) * prod((x_query(i) - x(1:j-1)));
        end
    end
end

% 步骤 5: 计算插值结果
x_query = linspace(0, 2*pi, 100); % 查询点
y_query = newton_interp(x, coefficients, x_query);

% 步骤 6: 绘制插值结果
figure;
plot(x, y, 'o', 'MarkerFaceColor', 'r', 'DisplayName', 'Data points');
hold on;
plot(x_query, y_query, 'b-', 'LineWidth', 2, 'DisplayName', 'Newton Interpolation');
title('Newton Interpolation for sin(x)');
xlabel('x');
ylabel('y');
legend show;

差分表是一个方阵，用于存储数据点的差分值。对于一组数据点 (x0,y0),(x1,y1),…,(xn,yn)，差分表 dd_table 会包含原始的 y值以及它们的一阶、二阶等差分，直到 n阶差分。差分表通常如下所示：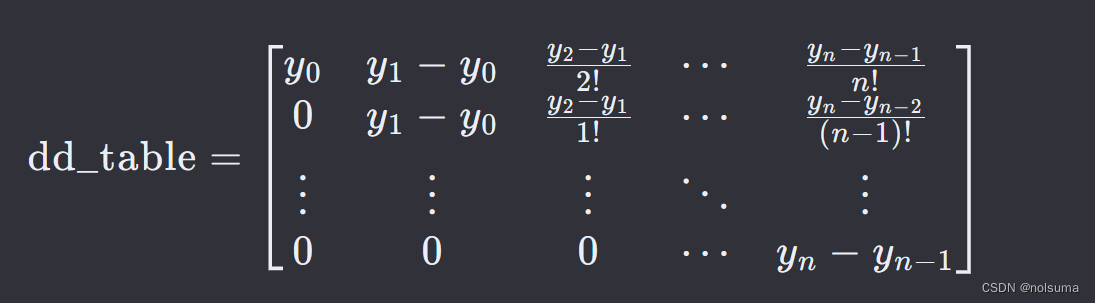

差分表的构建遵循特定的递归关系，每一行表示 y 值相对于前一行的差分，并且每行的差分阶数递增。在牛顿插值多项式中，差系数是差分表第一列的元素，即原始 𝑦 值以及它们的差分。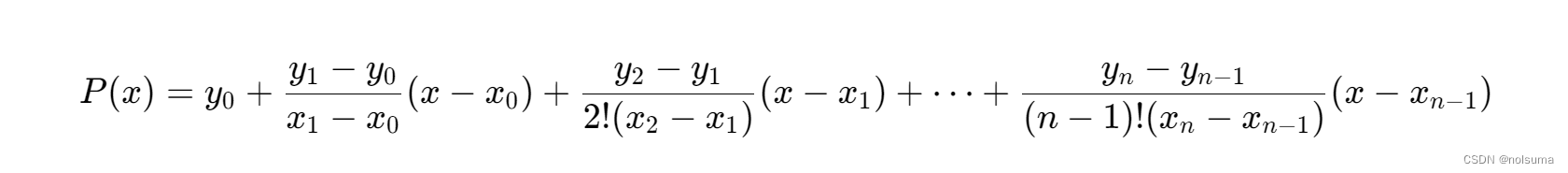

每一项都包含了一个差系数（差分表第一列的元素）和一个 x 的下降幂次项。差系数与 x的下降幂次的乘积，以及它们前面的系数（阶乘的倒数），共同构成了牛顿插值多项式的完整表达。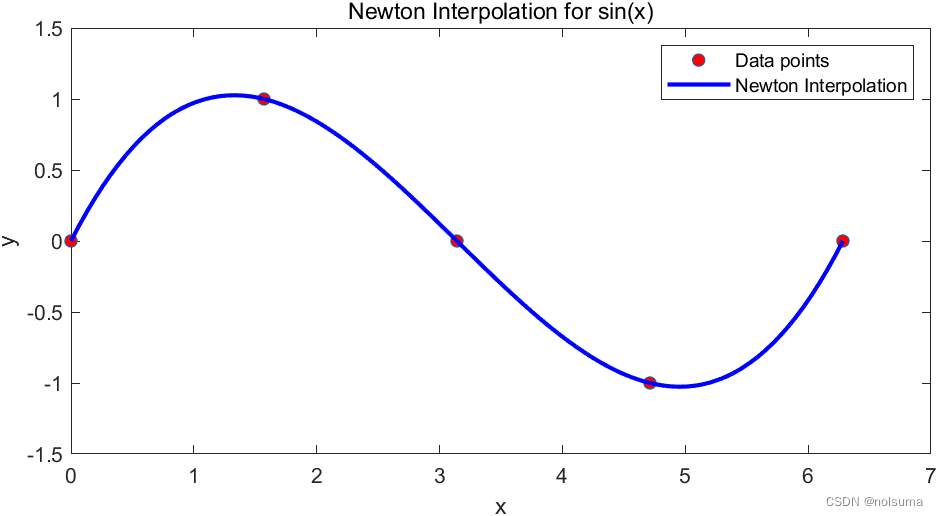

样条插值 (Spline Interpolation)

         对于自然样条插值，还会加上：
         自然边界条件：在区间的两端点 x0​ 和 xn处，二阶导数被设置为零，即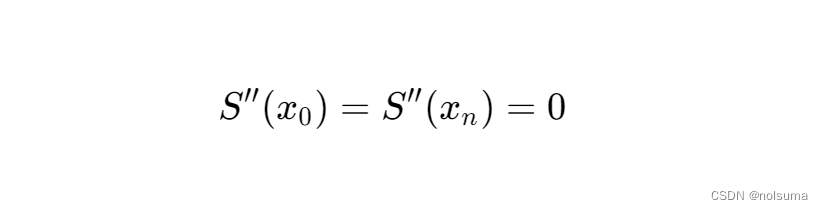

          二阶导数连续性：在每个数据点 xi上，样条曲线 S(x)的二阶导数（曲率）必须连续。

 

对于自然样条插值，还会加上：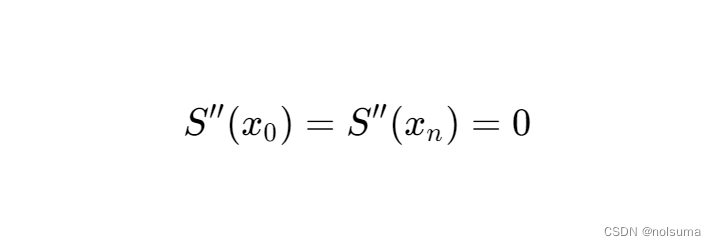

二阶导数连续性：在每个数据点 xi​ 上，样条曲线 S(x) 的二阶导数（曲率）必须连续。

1. 包括自然样条、周期样条等。

   样条插值通常分为几种类型，包括：
    线性样条：最简单的样条类型，由线性多项式段组成，保证值的连续性，但不保证导数的连续性。
   二次样条：由二次多项式段组成，保证值和一阶导数的连续性。
   三次样条：最常用的样条类型，由三次多项式段组成，保证值、一阶导数和二阶导数的连续性。
    

2. 什么是样条插值
   
    

   这些系数 𝑎𝑖,𝑏𝑖,𝑐𝑖是通过样条条件确定的，这些条件包括：
   插值条件：在每个数据点 xi上，样条曲线 S(x) 必须等于 yi。
   一阶导数连续性：在每个数据点 xi上，样条曲线 S(x) 的一阶导数（斜率）必须连续。

   % 步骤 1: 创建数据点
   x = [0, 1, 3, 4, 5]; % x坐标
   y = [0, 0.5, 2, 1.5, 1]; % y坐标，对应的函数值
   
   % 步骤 2: 使用spline函数进行样条插值
   % spline函数将返回样条曲线的控制点和系数
   tck = spline(x, y);
   
   % 步骤 3: 在更密集的点集上评估样条插值
   % 这将用于绘制平滑的曲线
   x_fine = linspace(min(x), max(x), 1000); % 生成细分的x坐标点
   y_fine = ppval(tck, x_fine); % 使用ppval在细分点上评估样条曲线
   
   % 步骤 4: 可视化原始数据点和样条插值曲线
   figure; % 创建一个新图形窗口
   plot(x, y, 'o', 'MarkerFaceColor', 'r', 'DisplayName', 'Data Points'); % 绘制原始数据点
   hold on; % 保持当前图形，以便在同一图形上绘制样条曲线
   plot(x_fine, y_fine, 'b-', 'DisplayName', 'Spline Interpolation'); % 绘制样条插值曲线
   title('Spline Interpolation Example');
   xlabel('x');
   ylabel('y');
   legend show; % 显示图例
   hold off; % 取消持续绘图状态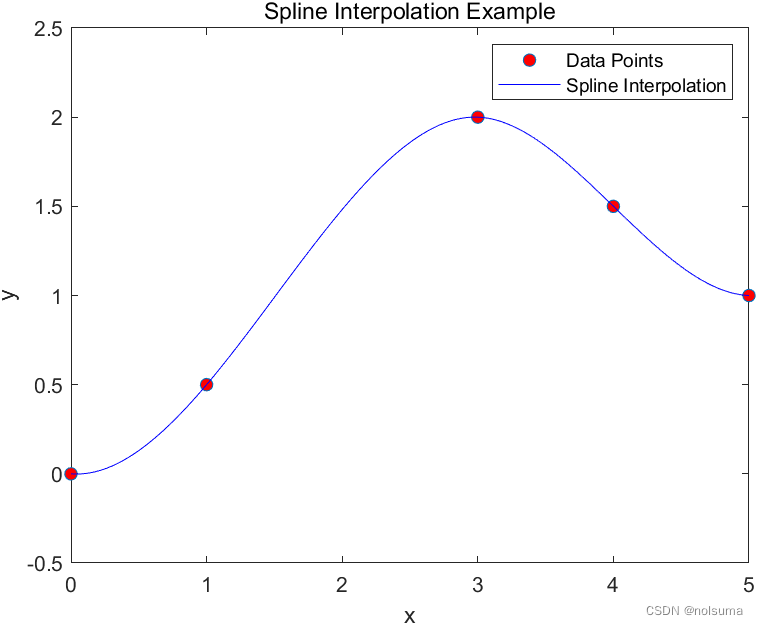

   
   
   自然样条插值

3. 自然样条插值通常指的是三次自然样条插值，它是一种特殊的样条插值方法，其中“自然”一词指的是在插值区间的边界处，二阶导数（即曲率）被设置为零。这种插值方法适用于不希望在边界处产生较大曲率的情况。
   

   % 步骤 1: 生成或获取复杂数据
   % 例如，我们生成一些正弦波数据，但带有随机噪声
   x = linspace(0, 2*pi, 50); % 创建50个等间距的点
   y = sin(x) + rand(size(x)) * 0.5; % 正弦函数加上随机噪声
   
   % 步骤 2: 使用MATLAB的spline函数进行自然样条插值
   % spline函数的第一个输出是分段多项式的节点（knots），
   % 第二个输出是分段多项式的系数
   tck = spline(x, y);
   
   % 步骤 3: 评估插值多项式
   % 我们创建一个密集的点集来评估插值结果
   x_fine = linspace(0, 2*pi, 1000);
   y_fine = ppval(tck, x_fine);
   
   % 步骤 4: 可视化结果
   figure;
   plot(x, y, 'o', 'MarkerFaceColor', 'r', 'DisplayName', 'Original Data');
   hold on;
   plot(x_fine, y_fine, 'b-', 'LineWidth', 2, 'DisplayName', 'Natural Spline Interpolation');
   title('Natural Spline Interpolation');
   xlabel('x');
   ylabel('y');
   legend show;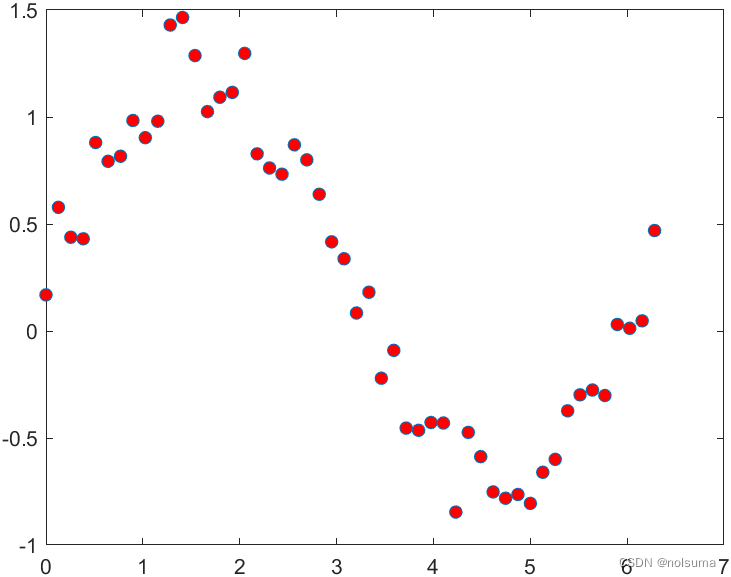

   
   
   
   
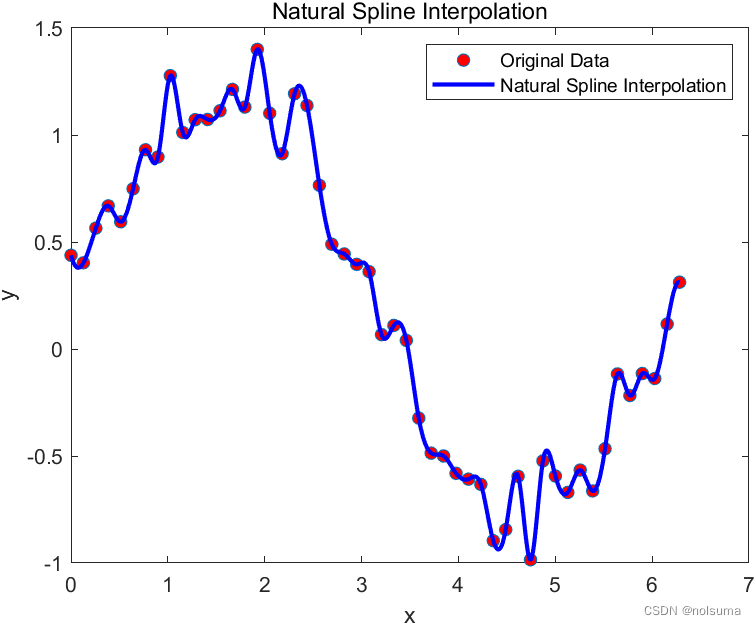
   关键讲解：
    

   x_fine = linspace(0, 2*pi, 1000); % 创建一个更密集的点集
   y_fine = ppval(tck, x_fine); % 在这些点上评估样条曲线

   ppval 函数用在密集点集 x_fine 上评估样条曲线。这样可以得到一个在原始数据点之间平滑的插值。三次样条曲线是设计为在数据点之间平滑过渡的，因此它不会捕捉到原始数据中的高频随机波动（即噪声）这是它的平滑特性，样条曲线是分段多项式，每个多项式段只影响其邻近的数据点，进行局部逼近。自然样条在边界处的二阶导数为零，这有助于避免在曲线两端产生不切实际的波动。

4. 周期样条插值
    

对于给定的一组数据点 (xi,yi)（其中 i=1,2,…,n且 x1<x2<⋯<xn），并且假设数据点是周期性的，即 y1=yn，周期样条插值S(x)是一个三次样条函数，满足以下条件：

1. 
   
   对于matlab来说，并不需要了解周期样条插值的原理，原因是matlab中内置一个csape 函数
    

   % 生成数据点
   x = linspace(0, 2*pi, 10); % 创建10个等间距的点，涵盖一个周期
   y = sin(x) + 0.1*randn(size(x)); % 在正弦波上添加一些高斯噪声
   
   % 显示数据点
   disp('Data points:');
   disp(table(x', y', 'VariableNames', {'x', 'y'}));
   
   % 绘制数据点
   figure; % 创建一个新图形窗口
   plot(x, y, 'o', 'DisplayName', 'Data points'); % 绘制数据点
   title('Data Points for Periodic Spline Interpolation'); % 图形标题
   xlabel('x'); % x轴标签
   ylabel('y'); % y轴标签
   grid on; % 打开网格
   legend show; % 显示图例
   
   % 使用周期样条插值
   pp = csape(x, y, 'periodic'); % 创建周期样条对象，指定为周期性数据
   
   % 生成查询点
   x_query = linspace(0, 2*pi, 100); % 创建100个点用于评估插值结果
   y_query = ppval(pp, x_query); % 在查询点上评估样条插值
   
   % 绘制插值结果
   hold on; % 保持当前图形，以便在同一图形上绘制插值结果
   plot(x_query, y_query, '-', 'DisplayName', 'Periodic Spline'); % 绘制插值曲线
   
   % 绘制原始正弦函数，用于比较
   plot(x_query, sin(x_query), '--', 'DisplayName', 'Original sin(x)'); % 绘制原始正弦波
   legend show; % 显示图例
   title('Periodic Spline Interpolation'); % 设置图形标题
   xlabel('x'); % 设置x轴标签
   ylabel('y'); % 设置y轴标签
   grid on; % 打开网格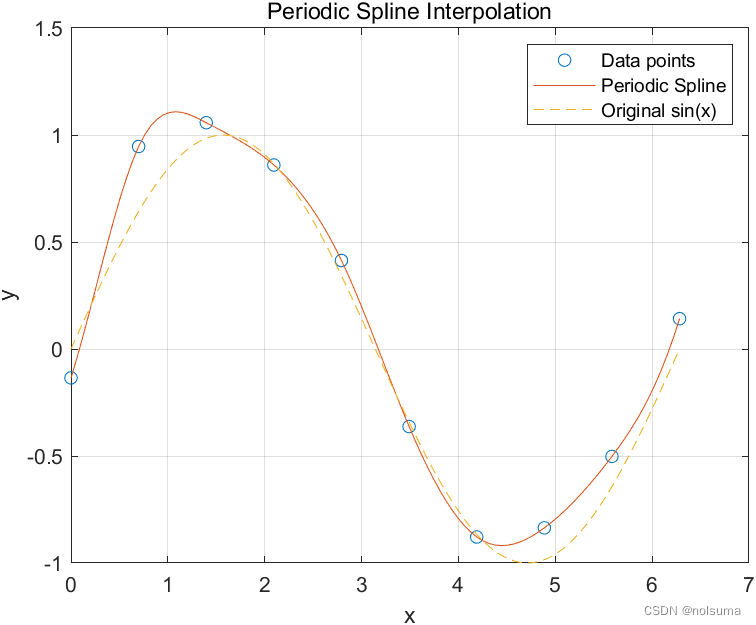

   
    

1. 分段插值 (Piecewise Interpolation)

   • 什么是分段插值：

   • 将一个区间分成多个子区间，并在每个子区间上使用不同的插值多项式来逼近数据点。

   • 分段线性插值：

   • 分段线性插值（Piecewise Linear Interpolation）是一种简单的插值方法，它将数据点通过直线段连接起来，以逼近给定的数据点集合。这种插值方式在每个数据点之间创建一个线性（一次多项式）段，因此得名“分段线性”。
     假设我们有数据点 (x0​,y0​),(x1​,y1​),…,(xn​,yn​)，分段线性插值会在每对相邻的数据点(xi​,yi​) 和 (xi+1​,yi+1​) 之间构建一条直线。对于 x 在 xi 和 xi+1之间的插值 y 可以通过以下线性方程计算：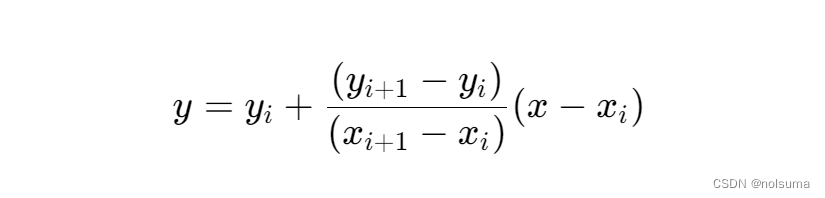
     
     首先创建新的脚本piecewise_linear_interpolation.m

     % piecewise_linear_interpolation.m
     function y_interp = piecewise_linear_interpolation(x_data, y_data, x_query)
         n = length(x_data);
         y_interp = zeros(size(x_query));
         
         for i = 1:n-1
             idx = x_query >= x_data(i) & x_query < x_data(i+1);
             m = (y_data(i+1) - y_data(i)) / (x_data(i+1) - x_data(i));
             y_interp(idx) = m * (x_query(idx) - x_data(i)) + y_data(i);
         end
         idx = x_query >= x_data(end);
         y_interp(idx) = m * (x_query(idx) - x_data(end)) + y_data(end);
     end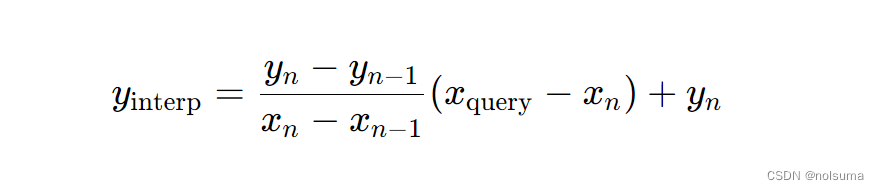

     
      

     % 主脚本
     % 步骤 1: 生成复杂数据
     x = linspace(0, 10, 50); % 创建50个等间距的点
     y = sin(x) + cos(x) + 0.5 * randn(size(x)); % 复杂的正弦余弦波加上随机噪声
     
     % 步骤 3: 执行分段线性插值
     x_query = linspace(min(x), max(x), 1000); % 创建查询点集
     y_interp = piecewise_linear_interpolation(x, y, x_query); % 调用函数进行插值
     
     % 步骤 4: 可视化结果
     figure;
     plot(x, y, 'o', 'MarkerFaceColor', 'r', 'DisplayName', 'Original Data Points');
     hold on;
     plot(x_query, y_interp, 'b-', 'LineWidth', 2, 'DisplayName', 'Piecewise Linear Interpolation');
     title('Piecewise Linear Interpolation of Complex Data');
     xlabel('x');
     ylabel('y');
     legend show;
     grid on;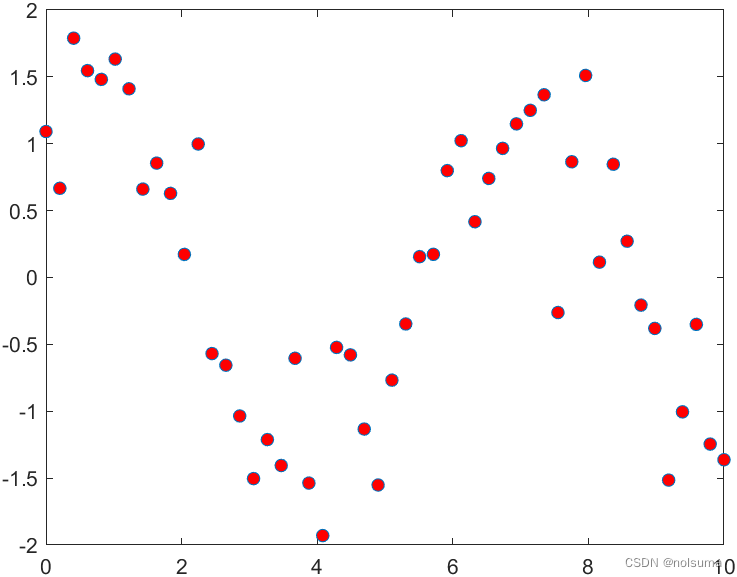

     
     
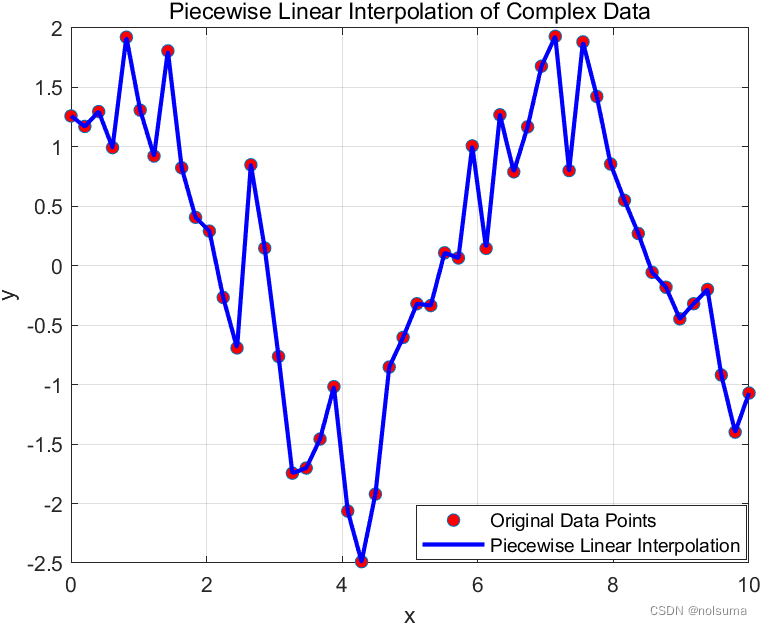
     分段线性插值它做了什么，为什么可以去除噪点，又是怎么确定曲线的？

   • 分段线性插值的基本概念：
     线性逼近：在两个相邻的数据点 (xi​,yi​) 和(xi+1​,yi+1​) 之间，分段线性插值确实使用一条直线y=mx+b 来逼近数据。这条直线的参数 m（斜率）和 b（截距）。
     分段：整个数据集被分成多个段，每一段都有一个线性函数。每个线性函数仅在相邻数据点之间有效。
     插值点：对于任意查询点 𝑥𝑞​，确定它落在哪个数据段内，并使用相应的线性函数计算 yq。
     平滑效应：由于分段线性插值使用直线连接数据点，它会忽略数据中的高频波动，这些高频波动往往是噪声。
     局部逼近：分段线性插值仅考虑局部数据点，因此它不会像全局多项式插值那样在整个数据集上拟合一个高阶多项式，从而减少了过拟合和噪声放大的风险。

   • 如何确定曲线：
     斜率计算：对于每个分段，计算两个相邻数据点间的斜率。
     截距确定：知道斜率和一个数据点，可以确定直线的截距。
     线性方程：对于每个分段，构建一个线性方程 y=mx+b，用于计算该分段内任意点的 y值。

   • 分段多项式插值：

   • 样条插值通常使用三次多项式段，而分段多项式插值可以使用不同阶数的多项式。

     % 创建 x 数据点
     x = linspace(0, 10, 20);
     
     % 创建 y 数据点，使用一个复杂的函数
     y = sin(x) + 0.5 * cos(2*x) + 0.3 * randn(size(x));  % 加入一些噪声
     
     % 绘制原始数据点
     figure;
     plot(x, y, 'o', 'DisplayName', '原始数据点');
     hold on;
     
     % 创建新的 x 点用于插值
     xq = linspace(0, 10, 100);
     
     % 使用分段多项式插值
     yq_linear = interp1(x, y, xq, 'linear');
     plot(xq, yq_linear, '-r', 'DisplayName', '分段多项式插值');
     
     % 使用三次样条插值
     yq_spline = interp1(x, y, xq, 'spline');
     plot(xq, yq_spline, '-b', 'DisplayName', '三次样条插值');
     
     % 添加图例和标签
     legend;
     xlabel('x');
     ylabel('y');
     title('分段多项式插值 vs 三次样条插值');
     hold off;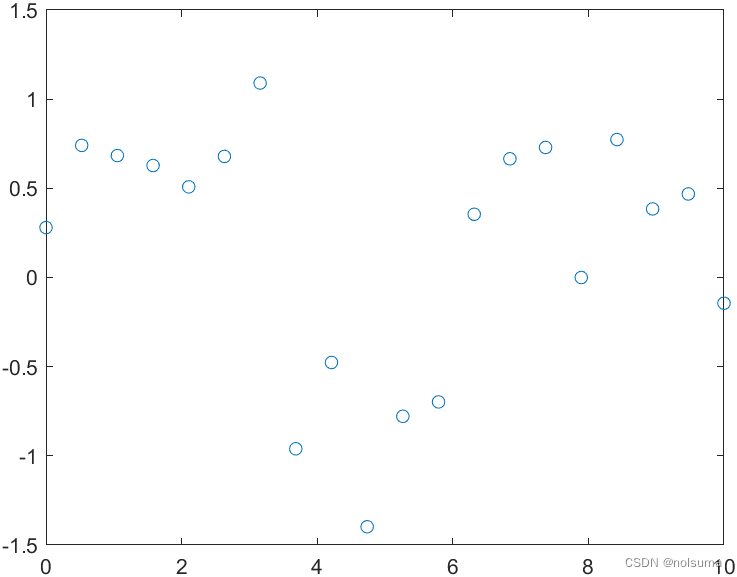

     
     

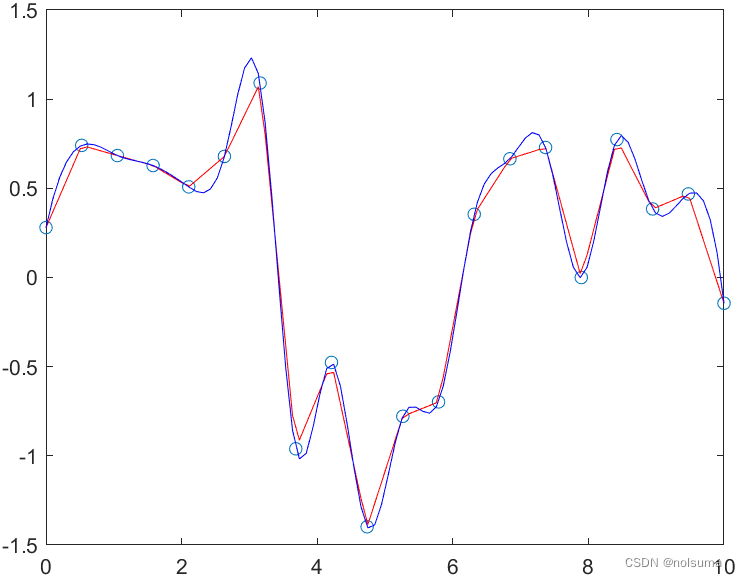
2. 径向基函数插值 (Radial Basis Function Interpolation)

   • 使用径向基函数来估计数据点之间的值。

   • 径向基函数：径向基函数是一类特殊类型的函数，它们仅依赖于输入点到某个中心点的距离，即ϕ(x)=f(∥x−c∥) ，其中 x是输入点，c是中心点，∥⋅∥ 表示欧几里得范数。常见的径向基函数包括高斯函数、多二次函数、逆多线性函数等。尤其适用于多维数据。
     线性组合：在RBF插值中，目标函数 𝑓(𝑥)被近似为一组径向基函数的线性组合：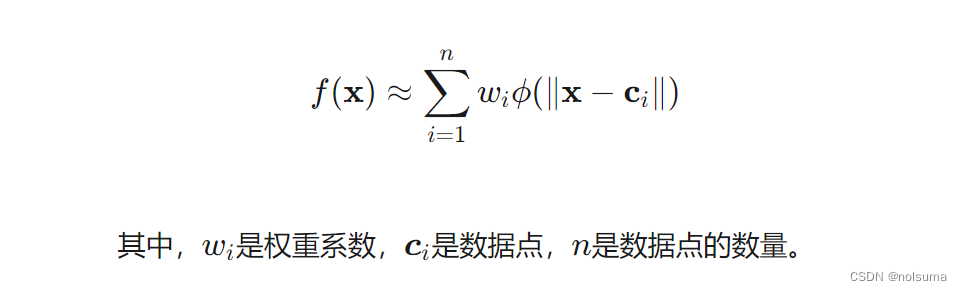
     
     权重系数：权重系数 wi​ 可以通过最小二乘法或其他优化技术来确定，使得插值函数在已知数据点上与目标函数尽可能吻合。
     平滑性：RBF插值通常会产生一个平滑的曲面，因为它是通过连续的基函数构建的。
     局部逼近：每个径向基函数仅在中心点附近有较大值，因此RBF插值具有局部逼近的特性，即每个点的插值主要由其附近的数据点决定。
     应用：

   • RBF插值在许多领域都有应用，包括但不限于：计算机图形学：用于生成平滑曲面。机器学习：作为径向基网络的基础，用于模式识别和分类。信号处理：用于数据平滑和噪声去除。空间数据分析：用于地理信息系统（GIS）中的数据插值。
     多维插值：RBF插值特别适用于多维空间中的插值问题，因为它不需要像多项式插值那样确定多维多项式的系数。适应性：RBF插值可以适应数据点的分布，因为它不是基于全局参数（如多项式的阶数），而是基于局部的径向基函数。
     1.导入pdist2 函数，清除 MATLAB 的函数和路径缓存

     clear functions
     rehash toolboxcache

     2.创建随机复杂数据点：
      

     n = 20; % 数据点数
     x = rand(n, 1) * 10; % x 坐标
     y = rand(n, 1) * 10; % y 坐标
     z = sin(x) + cos(y); % 目标函数值
     %% 生成了20个随机的数据点，其坐标在0到10之间，使用正弦和余弦函数的组合计算每个点的z值

     3.创建插值网格、定义径向基函数：
      

     [xq, yq] = meshgrid(linspace(0, 10, 100), linspace(0, 10, 100));
     % 使用meshgrid函数创建100x100的网格，用于在插值后绘制三维曲面。
     
     epsilon = 1; % 参数，可以调整
     rbf = @(r) sqrt((epsilon*r).^2 + 1);
     定义一个多二次径向基函数（Multiquadric），RBF插值中常用的一种函数形式。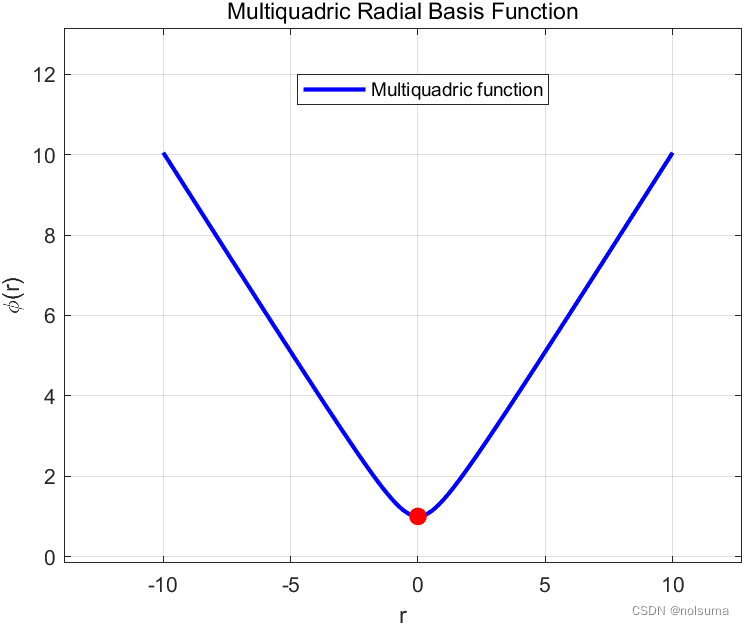

     
     
             其中，r是从原点到某个点的距离，可以表示为r=∥x−c∥，这里 x 是任意一点，𝑐是中心点。
     
     4.计算距离矩阵
      

     X = [x, y];
     m = size(X, 1);
     D = pdist2(X, X); % m x m 的距离矩阵
     Phi = rbf(D);
     
     %% 计算所有数据点之间的距离，并应用RBF来构建一个距离矩阵Phi。

     距离矩阵是一个方阵，其中的元素表示数据集中各点之间的距离，被用于评估径向基函数：将距离矩阵中的每个元素 D(i,j) 代入选定的径向基函数 ϕ 中，得到一个新的矩阵 Φ，其元素 Φ(i,j)=ϕ(D(i,j))。
     
     对于一个给定的数据集 X={x1,x2,…,xn}，距离矩阵 D 定义为：

     D(i,j)=∥xi​−xj​∥

     其中，∥⋅∥ 表示两点之间的欧几里得距离（在多维空间上）：
     
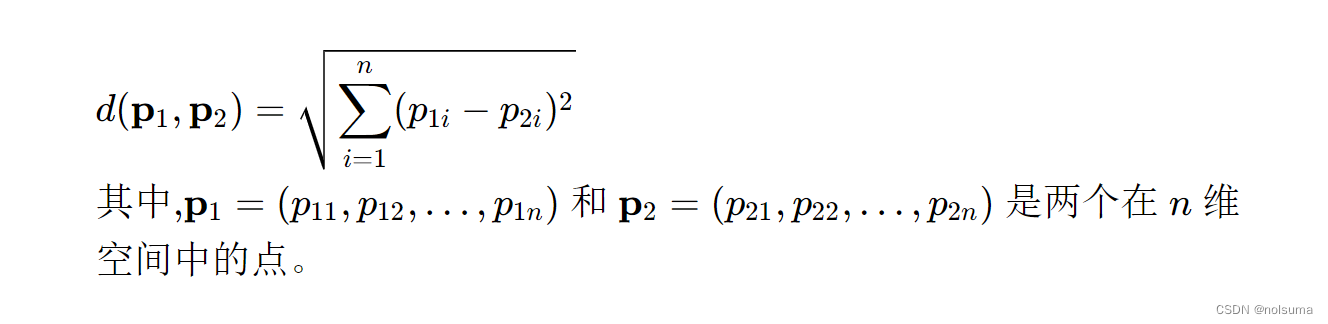
     对于一个 n×n的距离矩阵，D(i,i)通常是 0，表示点到自身的距离，而 D(i,j)和 D(j,i)是对称的，因为距离是无向的。

     5.求解权重、计算插值点的径向基函数值：

     w = Phi \ z;
     %% 使用MATLAB的左除运算符\来解决线性系统，从而得到插值权重w。
     
     Xq = [xq(:), yq(:)];
     Dq = pdist2(Xq, X);
     Phiq = rbf(Dq);
     
     %% 对于插值网格上的每个点，计算其到原始数据点的欧氏距离，并应用RBF

     求解权重是确定如何将各个径向基函数的值加权求和以匹配目标函数值的过程。
     
     假设我们有一组数据点 (xi,zi)，其中zi是数据点 xi 的已知函数值。RBF插值的目标是找到一个函数f(x)，它在每个数据点 xi上与 zi尽可能接近（"接近"意味着插值函数 f(x) 在每个数据点 xi上的值应该尽可能地与实际的观测值 zi 相匹配）。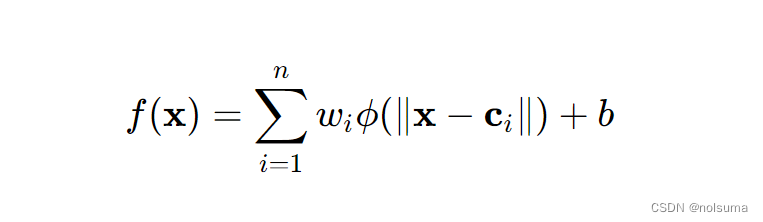
     
     其中，wi 是权重系数，ci 是中心点（可以是数据点或选定的其他点），b 是偏置项，n是中心点的数量。

     求解权重 wi 和偏置项 b通常涉及解决一个线性系统：

     Aw=z

     其中，A是由径向基函数值组成的矩阵 Φ（可能还包括一个用于偏置项的单位矩阵），w是包含权重和偏置项的向量，z是数据点的函数值向量。
     
     6.进行插值、将插值结果重塑为网格形式：
      

     zq = Phiq * w;
     %% 使用RBF值和权重来计算插值网格上每个点的z值。
     
     zq = reshape(zq, size(xq));
     %% 将一维插值结果向量zq重塑为与xq和yq对应的二维网格

     7.绘制原始数据点和插值结果、添加图例和标签：
      

     figure;
     scatter3(x, y, z, 'o', 'filled');
     hold on;
     surf(xq, yq, zq, 'EdgeColor', 'none');
     hold off;
     
     title('径向基函数插值');
     xlabel('X');
     ylabel('Y');
     zlabel('Z');
     legend('原始数据点', '插值结果');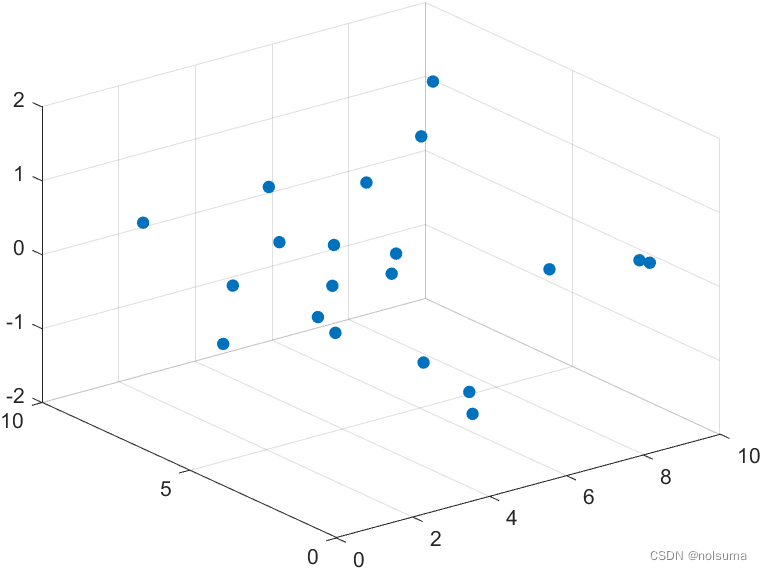

     
     
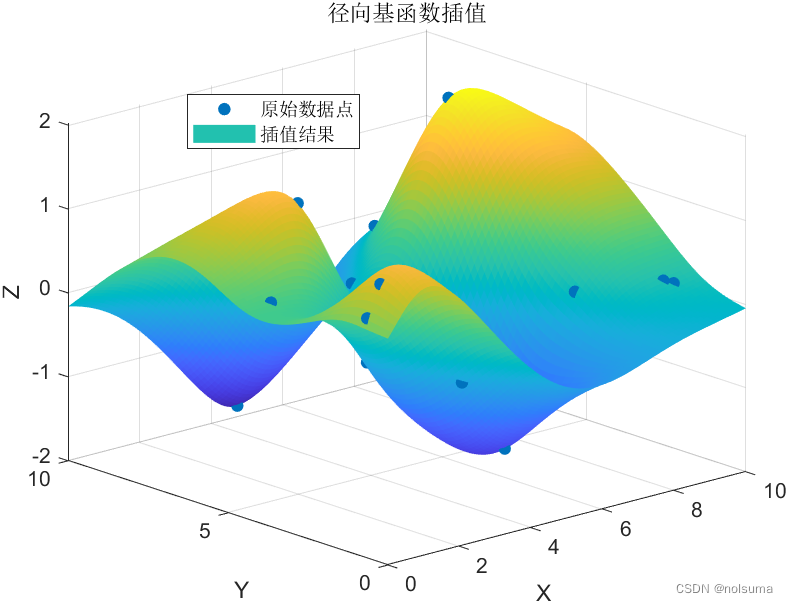
     关键讲解
     使用 Multiquadric 径向基函数，定义为：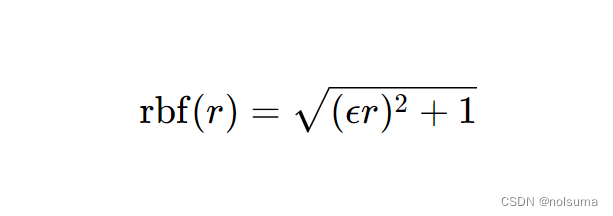
     
     其中 𝜖 是一个可调参数，它控制着函数的形状和宽度。