2024年NOJ详解(51-80)

由于csdn字数限制，这篇只放置51-80的题目。
1-50的题解
81-100的题解

写在前面

​ 本文旨在分享有关NOJ题目的思路和做法以及注意事项（不保证我分享代码的简洁和高效），不鼓励 同学们直接Copy代码。希望大家在读完本文后能够有所收获，也希望同学们能够对我其中的错误进行指正。发布顺序不固定。其中发布的代码均已确认AC。

其中56题字符串替换和77题日出日落没法做出来。前一个不知道为什么没办法AC，后一个算法下载地址进不去。

小建议：推荐大家可以尝试使用Clion这个IDE，在纠正代码错误方面十分好用。以及Snipaste截图软件，可以把截图始终显示在屏幕最上方，不必再来回看题。而git可帮助你进行代码的管理，如果你有了新思路但又怕这个是错的话，这个软件就派上用场了。

关于NOJ

​ NOJ是西北工业大学开设的C语言实验课的作业，同时也是上课的主要内容。60题AC是报名期末考试的条件。但个人觉得其中部分题目难度过于大了，而这部分难度不是体现在编程上，反而体现在数学上，这也是我个人想进行题目解析和分享的一个原因。

前排重要提醒：NOJ检测程序本质上是C++，只是C++完全兼容C语言，所有你不可以使用C++关键词去做变量名称,例如：new,and,or。虽然这并不会在C语言程序中报错，但是在NOJ检测时候会出现CE错误。所以当出现CE错误时，可以建立一个.cpp文件在IDE中进行检测，可能就是我说得这个问题。此外：scanf_s()函数在NOJ检测程序中不存在，若是使用，或造成CE错误。以及fgets()不知道为什么总是没办法通过，只能用scanf("%[^\n]", str)替代。

关于数学部分证明：若是个人认为证明相对比较简单就会将证明过程写在下面，但若是觉得证明过程十分容易找到或是比较繁杂，就请读者自行查找了。😊

---

详解

051 大小写交换

#include <stdio.h>
#include <string.h>
#include <ctype.h>  //   引入tolower()和toupper()函数
char str[10000];  // 全局定义一个大数组
int main(){
    fgets(str, 10000, stdin);
    int len = strlen(str);  // 记录字符串的长度
    for(int i = 0; i < len; i++){
        int character = str[i];  // 要检测的字符
        if((64 < character) && (character<91))  // 如果为大写字母
            str[i] = tolower(str[i]);
        if((96 < character) && (character < 123))  //如果为小写字母
            str[i] = toupper(str[i]);
    }
    puts(str);
    return 0;
}

这里按照ASCII检测字符(或者直接写'A'这种也可以)并使用tolower()和toupper()函数就行。

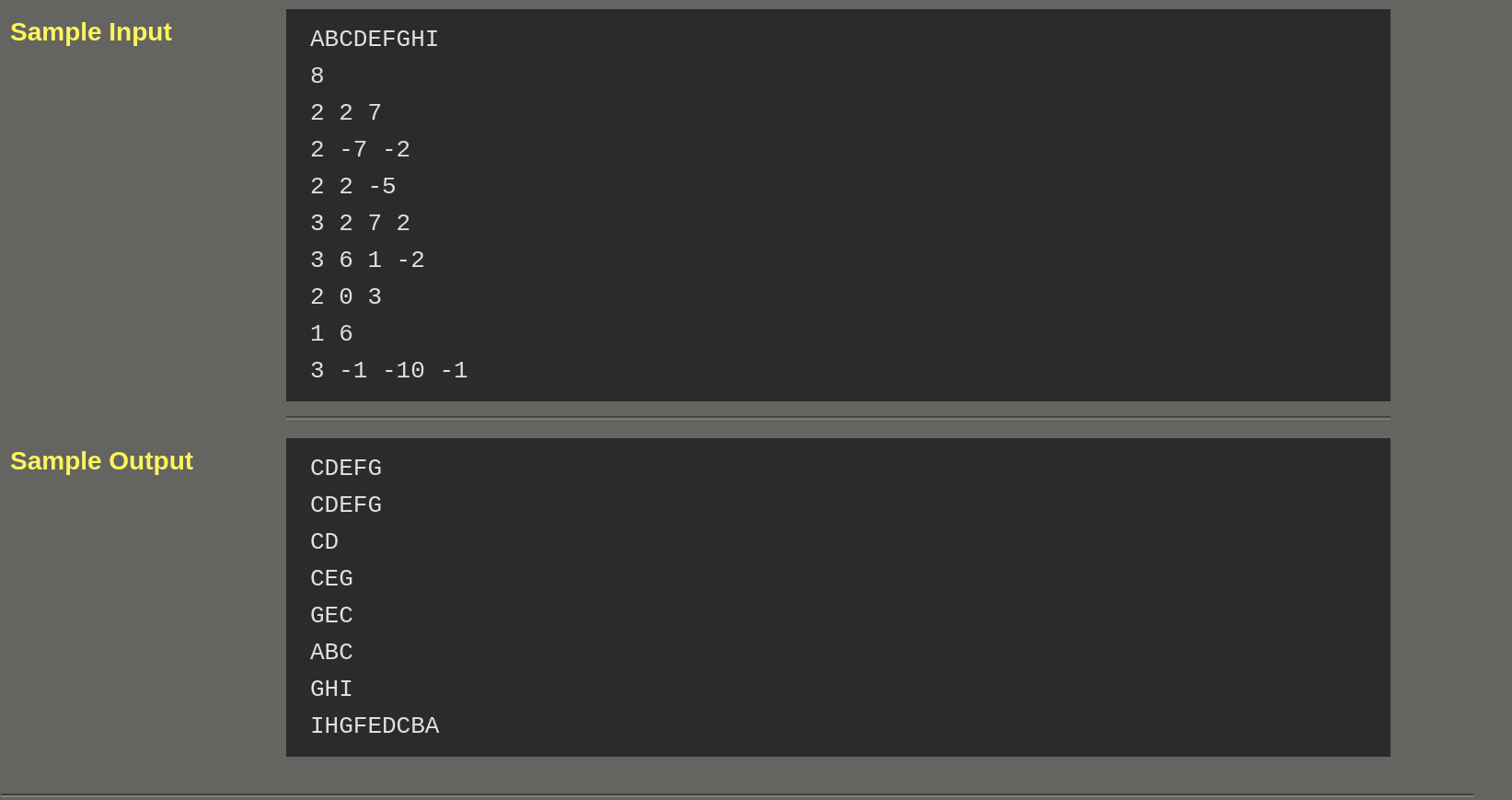
052 字符串切片

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
void cutString(int n, char *str, char **Reserve, int *num, int **input);
// 进行字符串切片操作,n为操作的数量，str为需要操作的字符串,Reserve存储切片结果，num是每行有几个参数，input为切片索引
int negative_to_positve(int index, int len);
// 将负数索引转化为正数索引，index为要转化的索引，len为字符串长度
int main(){
    int n;//n为有n行数据需要处理
    char *str=(char*)malloc(10000*sizeof(char));  // 需要操作的字符串
    scanf(" %s %d", str, &n);
    char **forReserve = (char**)malloc(n*sizeof(char*));  // 存储结果字符串
    int *num = (int*)malloc(n*sizeof(int));  // 存储每行的参数个数
    int **input = (int**)malloc(n*sizeof(int*));  // 输入的数据
    for(int i=0; i<n; i++){
        forReserve[i] = (char*)malloc(10000*sizeof(char));
        scanf(" %d", &num[i]);  // 参数个数
        input[i]=(int*)malloc(num[i]*sizeof(int));
        for(int j=0; j<num[i]; j++)
            scanf(" %d",&input[i][j]);
    }
    cutString(n, str, forReserve, num, input);
    for(int i=0; i<n; i++)  // 将结果打印
        printf("%s\n",forReserve[i]);
    //释放堆并置空
    free(num);
    num = NULL;
    for(int i=0; i<n; i++){
        free(input[i]);
        input[i]=NULL;
        free(forReserve[i]);
        forReserve[i]=NULL;
    }
    free(input);
    input = NULL;
    free(forReserve);
    forReserve = NULL;
    free(str);
    str = NULL;
    return 0;
}
void cutString(int n, char *str, char **Reserve, int *num, int **input){
    int stringLength = strlen(str);  // 记录字符串长度
    for(int i=0; i<n; i++){  // 依据参数数量截取字符串
        if(num[i] == 1){  // 参数的数量为1,截取参数后的所有字符串
            int len_res = 0;  // 记录截取结果的长度
            int start = negative_to_positve(input[i][0], stringLength);  // 获取参数下标，将负数转化为正数
            for(int j = start; j<stringLength; j++, len_res++)  // 将截取字符串存储起来
                Reserve[i][j-start] = str[j];
            Reserve[i][len_res] = '\0';  // 最后加上'\0'
        }
        else if(num[i] == 2){  // 参数数量为2，则步长为1,左闭右开区间
            int len_res = 0;  // 记录截取结果的长度
            int start = negative_to_positve(input[i][0], stringLength);  // 获取开始的位置，并将负数转化为正数
            int end = negative_to_positve(input[i][1], stringLength);  // 获取结束位置，将负数转为正数
            for(int j=start; j<end; j++, len_res++)  // 截取之间的字符串
                Reserve[i][j-start] = str[j];
            Reserve[i][len_res]='\0';  // 最后加上'\0'
        }
        else{  // 参数数量为3,开始，结束步长
            if(input[i][2] > 0){  // 如果步长为正数
                int len_res = 0;  // 记录截取结果的长度
                int start = negative_to_positve(input[i][0], stringLength);  // 获取开始的位置，并将负数转化为正数
                int end = negative_to_positve(input[i][1], stringLength);  // 获取结束位置，将负数转为正数
                int step = input[i][2];  // 步长
                for(int j=start; j<end; j+=step, len_res++)  // 按步长间隔存储字符串
                    Reserve[i][(j-start)/step] = str[j];
                Reserve[i][len_res] = '\0';  // 最后加上'\0'
            }
            if(input[i][2]<0){  // 步长为负数
                int len_res = 0;  // 记录截取结果的长度
                int start = negative_to_positve(input[i][0], stringLength);  // 获取开始的位置，并将负数转化为正数
                int end = negative_to_positve(input[i][1], stringLength);  // 获取结束位置，将负数转为正数
                int step = input[i][2];  // 步长
                for(int j=start; j>end; j+=step, len_res++)  // 倒序存储字符串
                    Reserve[i][(start-j) / (-1*step)] = str[j];
                Reserve[i][len_res] = '\0';
            }
        }
    }
}
inline int negative_to_positve(int index, int len){
    if(index >= 0)  // 索引本身大于0，则不操作
        return index;
    else  // 索引小于0则用长度加上。
        return len + index;
}

思路：这里需要将负数的索引转化为正数索引来方便运算。然后便是按照题目意思对原字符串进行截取并存储到新的字符串中。注意其中负数的步长需要倒序存入。

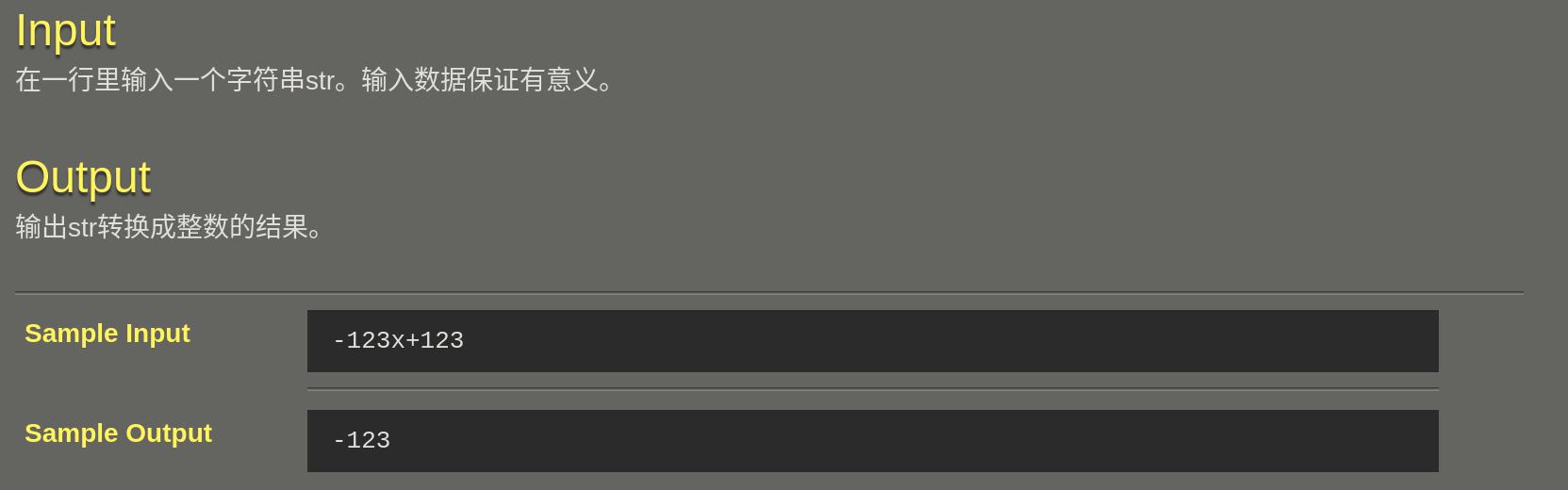
053 AtoI转换

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <ctype.h>

void DspaceZero(char *input, int stringLength);  // 删除前缀空格和0
void AtolConversion(char *input);  // 转换
void getTheNUmber(char *input,int stringLength);  // 将input截取数字部分
int main(void){
    char *input;  // 输入的字符串
    input=(char*) malloc(10000*sizeof(char));
    scanf(" %s",input);
    AtolConversion(input);  // 对其进行转化
    printf("%s",input);
    free(input);
    return 0;
}

void AtolConversion(char *input){
    char test1[12]="-2147483648";  // 用于比较的基准
    char test2[11]="2147483647";
    int big = 0;  // 判断数字是否超出范围的标志
    int stringLength= (int)strlen(input);  // 获取字符串的长度
    DspaceZero(input, stringLength);  // 删除前缀空格和0
    stringLength= (int)strlen(input);  // 获取删除空格之后的字符串长度
    getTheNUmber(input,stringLength);  // 截取字符串数字部分
    if(input[0]=='-'){  // 如果是负数
        if(strlen(input)>11) {  // 长度超过基准，说明绝对值大于它。
            for(int i=0;i<11;i++)  // 将基准复制给字符串
                input[i]=test1[i];
            input[11]='\0';  // 字符串结束标志
        }
        else if(strlen((input))==11){  // 或者字符串和基准长度相同
            for(int i=1;i<11;i++){  // 从前往后一次检验
                if(input[i]>test1[i]){  // 如果出现更大数字则标志为更大
                    big=1;
                    break;
                }
                else if(input[i]==test1[i])  // 如果该位相同则继续往后检验
                    continue;
                else break;  // 一位小于基准数字则意味着比基准小
            }
            if(big==1){  // 如果绝对值大，将基准复制给它
                for(int i=0;i<11;i++)
                    input[i]=test1[i];
                input[11]='\0';
            }
        }
    }
    else{  // 与负数检验相似
        if(strlen(input)>10) {
            for(int i=0;i<10;i++)
                input[i]=test2[i];
            input[10]='\0';
        }
        else if(strlen((input))==10){
            for(int i=0;i<10;i++){
                if(input[i]>test2[i]){
                    big=1;
                    break;
                }
                else if(input[i]==test2[i])
                    continue;
                else break;
            }
            if(big==1){
                for(int i=0;i<10;i++)
                    input[i]=test2[i];
                input[10]='\0';
            }
        }
    }
}

void DspaceZero(char *input, int stringLength){  // 删除前缀空格
    int ctr=0;  // 记录空格的个数
    if(input[0]==' '){  // 如果以空格开头
        for (int i = 0; i < stringLength; i++) {
            if (input[i] == ' ')  // 每有一个空格则计数一次
                ctr++;
        }
        for (int i = 0; i <= (stringLength - ctr); i++) {  // 将非空格数字前移
            input[i] = input[i + ctr];
        }
    }
    ctr=0;  // 记录0的个数
    if(input[0]=='0') {  // 如果以0开头
        for (int i = 0; i < stringLength; i++) {
            if (input[i] == '0')  // 每有一个0则计数一次
                ctr++;
        }
        for (int i = 0; i <= (stringLength - ctr); i++) {  // 将非0数字前移
            input[i] = input[i + ctr];
        }
    }
}

void getTheNUmber(char *input,int stringLength){
    int ctr=0;
    if(input[0]=='+'){  // 如果以正号开头，说明为正数
        for (int i = 1; i < stringLength; i++) {  // 不断读取数字
            if (isdigit(input[i]))
                ctr++;
            else break;
        }
        for(int i=0;i<ctr;i++)
            input[i]=input[i+1];
        if(ctr==0){  // 如果正号后面没有数字
            input[0]=0;
            input[1]='\0';
        }
        else input[ctr]='\0';
    }
    else if(input[0]=='-')  // 如果以负号开头，说明为正数
    {
        for (int i = 1; i < stringLength; i++) {  // 不断读取数字
            if (isdigit(input[i]))
                ctr++;
            else break;
        }
        if(ctr==0){  // 如果负号后面没有数字
            input[0]=0;
            input[1]='\0';
        }
        else input[ctr+1]='\0';
    }
    else if(isdigit(input[0])){  // 没有符号且有数字的情况
        for (int i = 1; i < stringLength; i++) {
            if (isdigit(input[i]))
                ctr++;
            else break;
        }
        input[ctr+1]='\0';
    }
    else {  // 开头为非符号非数字
        input[0]='0';
        input[1]='\0';
    }
}

思路：先去除开头的0和空格，并进行前移操作。再获取开头的数字。最后与最大范围进行比较。

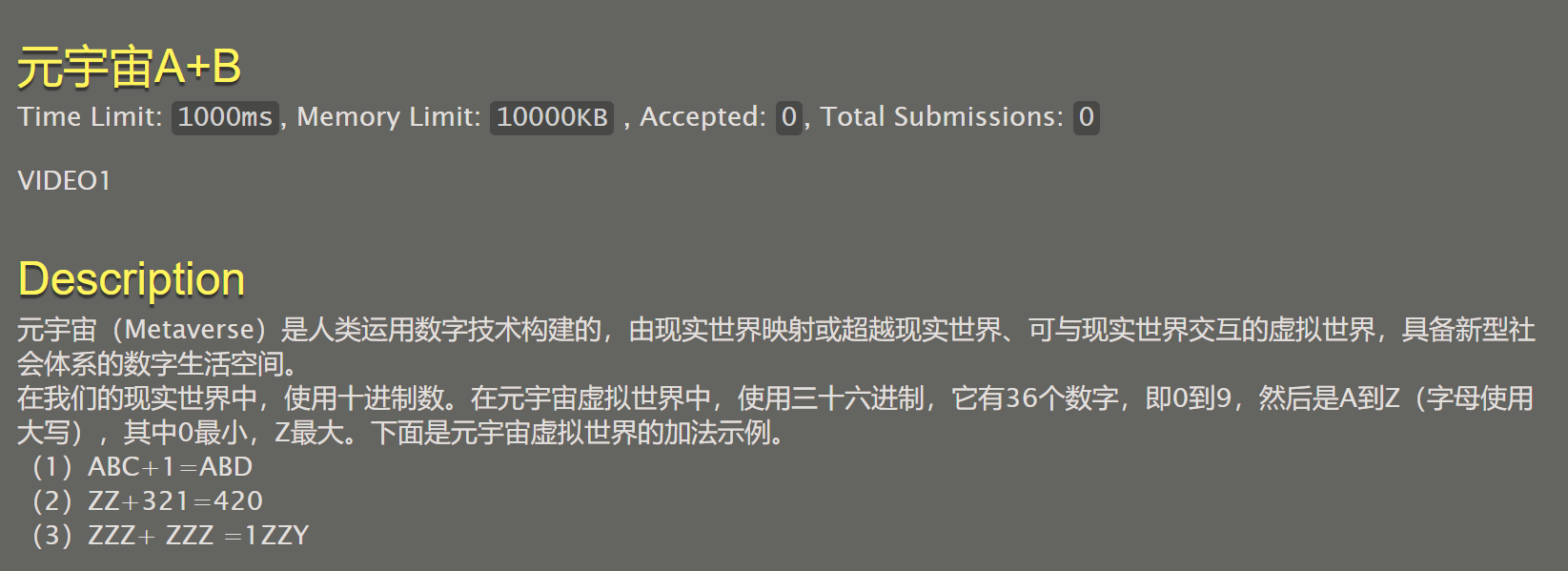
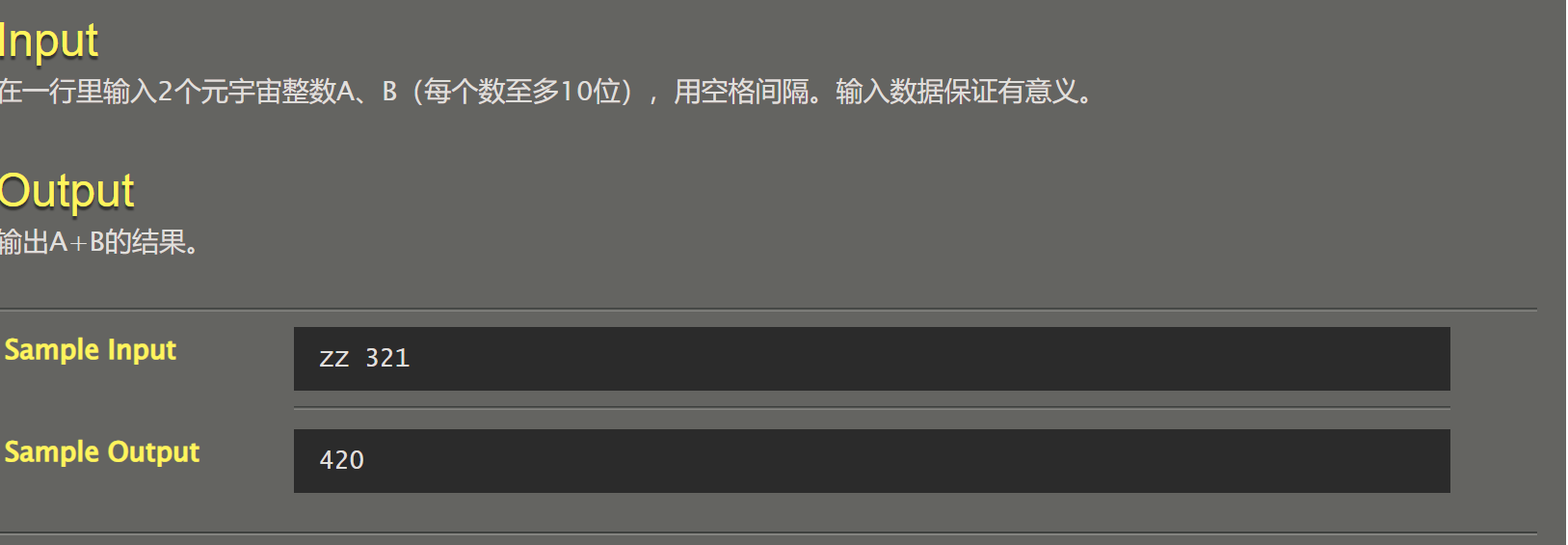
054 元宇宙A+B

#include <stdio.h>
#include <string.h>
void from36to10(char [], int);  // 将数组中的36进制数字转化为10进制,第二个参数为元素数量
void from10to36(char [], int);  // 将数组中的10进制转化为36进制,第二个参数为元素数量
void reverse(char [], int);  //  将数组的数字顺序翻转,第二个参赛为元素数量
void plus(char [], char [], char []);  // 计算两个元宇宙数字相加结果,并存储在第三个数组中

int main(void) {
    char num1[15] = {}, num2[15] = {}, array[20] = {};  //  分别用于存储元s宇宙数字和相加结果
    scanf(" %s %s", num1, num2);
    plus(num1, num2, array);
    printf("%s\n", array);
    return 0;
}

void plus(char num1[], char num2[],char array[]){
    reverse(num1, strlen(num1)), reverse(num2, strlen(num2));  //  将要相加的数字翻转
    from36to10(num1, strlen(num1)), from36to10(num2, strlen(num2));  //  将每位36进制转化为10进制方便计算 
    int len = 0;  // 记录最终数组的长度
    for(int i = 0; (num1[i] != '\0') || ( num2[i] != '\0'); ++i, ++len){  // 模仿竖式计算
        array[i] += num1[i] + num2[i];
        if(array[i] >= 36){
            array[1+i] += array[i] / 36;
            array[i] %= 36;
        }
    }
    if(array[len] != '\0')  // 判断是否存在最高位进位
        len++;
    from10to36(array, len);  // 将数组转化为36进制数字
    reverse(array, len);  // 将数组翻转使得符合正常顺序 
}

void from36to10(char array[], int n){
    for(int i = 0; i < n; i++)
        if( array[i] >= 'A')
            array[i] = 10 + (array[i] - 'A');  // 将字符数组当成数字数组存储数字
        else
            array[i] -= '0';
}
void from10to36(char array[], int n){
    for(int i = 0; i < n; i++)
        if(array[i] >= 10)
            array[i] = 'A' + (array[i] - 10);  // 将数字转化为字符存储
        else
            array[i] += '0';
}
void reverse(char array[], int n){
    for (int i = 0; i < (n / 2); ++i) {
        char temps = array[i];
        array[i] = array[n-1-i];
        array[n-1-i] = temps;
    }
}

思路：可以先将字符串中的字符转化为相应的数字，比如：'1’转换为1，'A’转化为10。之后将字符串翻转(加数可以不翻转，从后往前依次取数也可以)，按竖式加法的思想，每一位依次相加并进位就好。

注意：与普通的竖式加法不同，结果字符串从左到右存储计算结果。在这里我对于存储加数的字符串进行了初始化,保证了超出原来加数位数之后的每一位均为'\0'。如果没有进行初始化，那么需要对此时取的位数与加数的最大位数相比较，如果超过加数的最大位数那么取0。

055 Kids A+B

#include <stdio.h>
#include "stdlib.h"
#include "string.h"

int alphaToDigit(char *p);  // 英语变为数字
char *DigitToAlpha(int num);  // 数字变为英语
int main(void) {
    char *first;
    char *second;
    first=(char*)malloc(20*sizeof(char));
    second=(char*)malloc(20*sizeof(char));
    scanf(" %s %s",first,second);
    int f= alphaToDigit(first),s= alphaToDigit(second);  // 两个都转化为数字
    printf("%s", DigitToAlpha(f+s));  // 数字再转化为英语
    free(first);
    free(second);
    return 0;
}
int alphaToDigit(char *p){
    int check=1;
    for(int i=0;i< strlen(p);i++){  // 判断英语由几个部分组成
        if(p[i]=='-'){  // 存在短线则有两个部分
            check=2;
            break;
        }
        else check=1;
    }
    if(check==1){  // 一个部分则根据英语读取数字
        if(strcmp(p,"zero")==0)
            return 0;
        else if(strcmp(p,"one")==0)
            return 1;
        else if(strcmp(p,"two")==0)
            return 2;
        else if(strcmp(p,"three")==0)
            return 3;
        else if(strcmp(p,"four")==0)
            return 4;
        else if(strcmp(p,"five")==0)
            return 5;
        else if(strcmp(p,"six")==0)
            return 6;
        else if(strcmp(p,"seven")==0)
            return 7;
        else if(strcmp(p,"eight")==0)
            return 8;
        else if(strcmp(p,"nine")==0)
            return 9;
        else if(strcmp(p,"ten")==0)
            return 10;
        else if(strcmp(p,"eleven")==0)
            return 11;
        else if(strcmp(p,"twelve")==0)
            return 12;
        else if(strcmp(p,"thirteen")==0)
            return 13;
        else if(strcmp(p,"fourteen")==0)
            return 14;
        else if(strcmp(p,"fifteen")==0)
            return 15;
        else if(strcmp(p,"sixteen")==0)
            return 16;
        else if(strcmp(p,"seventeen")==0)
            return 17;
        else if(strcmp(p,"eighteen")==0)
            return 18;
        else if(strcmp(p,"nineteen")==0)
            return 19;
        else if(strcmp(p,"twenty")==0)
            return 20;
        else if(strcmp(p,"thirty")==0)
            return 30;
        else if(strcmp(p,"forty")==0)
            return 40;
        else if(strcmp(p,"fifty")==0)
            return 50;
        else if(strcmp(p,"sixty")==0)
            return 60;
        else if(strcmp(p,"seventy")==0)
            return 70;
        else if(strcmp(p,"eighty")==0)
            return 80;
        else if(strcmp(p,"ninety")==0)
            return 90;
    }
    else{  // 两个部分
        char *first;  // 存储第一个部分
        char *second;  // 存储第二个部分
        first=(char*)malloc(20*sizeof(char));
        second=(char*)malloc(20*sizeof(char));
        int ctr=0;
        for(int i=0;i< strlen(p);i++){
            if(p[i]=='-')
                break;
            ctr++;
            first[i]=p[i];
        }
        first[ctr]='\0';
        for(int i=(ctr+1);i< strlen(p);i++){
            second[i-ctr-1]=p[i];
        }
        second[strlen(p)-ctr-1]='\0';
        return alphaToDigit(first)+ alphaToDigit(second);  // 再使得第一和第二个部分分别转化为数字再相加
    }
}

char *DigitToAlpha(int num){
    if(num==0){
        return "zero";
    }
    if(num==1){
        return "one";
    }
    if(num==2){
        return "two";
    }
    if(num==3){
        return "three";
    }
    if(num==4){
        return "four";
    }
    if(num==5){
        return "five";
    }
    if(num==6){
        return "six";
    }
    if(num==7){
        return "seven";
    }
    if(num==8){
        return "eight";
    }
    if(num==9){
        return "nine";
    }
    if(num==10){
        return "ten";
    }
    if(num==11){
        return "eleven";
    }
    if(num==12){
        return "twelve";
    }
    if(num==13){
        return "thirteen";
    }
    if(num==14){
        return "fourteen";
    }
    if(num==15){
        return "fifteen";
    }
    if(num==16){
        return "sixteen";
    }
    if(num==17){
        return "seventeen";
    }
    if(num==18){
        return "eighteen";
    }
    if(num==19){
        return "nineteen";
    }
    if(num==20){
        return "twenty";
    }
    if(num==30){
        return "thirty";
    }
    if(num==40){
        return "forty";
    }
    if(num==50){
        return "fifty";
    }
    if(num==60){
        return "sixty";
    }
    if(num==70){
        return "seventy";
    }
    if(num==80){
        return "eighty";
    }
    if(num==90){
        return "ninety";
    }
    else{  // 数字无法转化为单个部分
        int n1, n2;  // 数字存储为两部分
        n1=num/10*10;  // 个位部分
        n2=num%10;  // 十位部分
        // 存储前半和后半部分的字符串
        char *s1=(char*)malloc(20*sizeof(char));
        char *s2=(char*)malloc(20*sizeof(char));
        strcpy(s1, DigitToAlpha(n1));
        strcpy(s2, DigitToAlpha(n2));
        // 将其拼接
        strcat(s1,"-");
        strcat(s1,s2);
        free(s2);
        return s1;
    }
}

思路：英语的有些数字只有一个部分，这部分可以进行罗列。另外一些数字则需要分为两个部分分别转化为数字再加起来。而数字转化为英语也是先看其能不能化为一个部分的英语单词，不能则分为个位和十位，分别转化再进行拼接。

057 字符串后缀

#include <stdio.h>
#include <string.h>
char suffix_compare(char [], char []);  // 比较字符串后缀,后一个为后缀
int main(){
    char str[1000], suffix[1000];  // 定义两个大数组
    scanf(" %[^\n] %[^\n]", str, suffix);
    if(suffix_compare(str, suffix))
        puts("Yes");
    else
        puts("No");
    return 0;
}
char suffix_compare(char str[], char suffix[]){
    int len_str = strlen(str);  // 记录字符串长度 
    int ctr = 0;  // 用来记录后缀有几个字符和字符串后缀相同
    for(int i = strlen(suffix)-1; i >= 0; i--)  // 从后往前依次比较
        if(suffix[i] == str[--len_str])
            ctr++;
        else  // 出现不同字符则直接结束
            break;
    if(ctr == strlen(suffix))
        return 1;
    else 
        return 0;
}

注意：这里如果使用fgets()函数会报出WA。不知道原因，只能使用%[^\n]这种scanf格式输入。表示输入除了\n之外的所有字符。

将字符串和要检测的后缀从后往前比较就好。

058 分离字符串

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
using namespace std;
void check(int len_1,int len_2,int *index,char *str,char *sep);
// 将字符串每次截取的结束位置记录在index中
int main(){
    char *str = (char*)malloc(1000*sizeof(char));  // 原字符串
    char *sep = (char*)malloc(1000*sizeof(char));  // 分隔字符串
    scanf(" %[^\n] %[^\n]", str, sep);  // 读取除了空格之外的所有字符 
    int len_1 = strlen(str);  // 原字符的长度
    int len_2 = strlen(sep);  // 分隔字符串的长度
    int *index = (int*)calloc(len_1, sizeof(int));  // 记录关键索引，初始化为0
    check(len_1, len_2, index, str, sep);
    if(index[0] == 0){  // 没有记录任何索引，将原字符串打印
        printf("%s\n", str);
        return 0;
    }
    int ctr = 0;  // 记录此时使用多少个索引
    do{
        if(ctr == 0){  // 第一个索引特殊考虑
            for(int i=0; i<index[ctr]; i++)
                printf("%c", str[i]);
            printf("\n");
        }
        if(index[ctr+1] == 0){  // 最后一个索引特殊考虑
            for(int i = index[ctr++]+len_2; i < len_1; i++)
                printf("%c", str[i]);
            printf("\n");
            break;
        }
        for(int i = index[ctr++]+len_2; i < index[ctr]; i++)  // 打印分隔符之间字符串
            printf("%c", str[i]);
        printf("\n");
    }while(index[ctr] != 0);
    return 0;
}
void check(int len_1,int len_2,int *index,char *str,char *sep){
    int ctr = 0;  // 记录的索引的个数
    for(int i=0; i<len_1; i++){  // 依次检索原字符串
        if(str[i] == sep[0]){  // 如果出现相同的字符
            int flag = 1;  // 判断是否分隔字符串完全出现
            for(int j=1; j<len_2; j++){  // 检验分隔字符串是否完全出现在原字符串中
                if(str[i+j] != sep[j]){  // 只要有一个字符不同，则没有完全出现
                    flag = 0;
                    break;
                }
            }
            if(flag){
                index[ctr++] = i;  // 记录此时的下标
                i += len_2-1;  // 并更新i的值,-1是因为之后循环内部会加1
            }
        }
    }
}

思路：要记录出现分隔字符串的位置，然后第一个和最后一个特殊判断，将中间的位置打印出来。

059 删除前后缀

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

void deleteprefix(char *str,char *word);  // 删除前缀
void deletepostfix(char *str,char *word);  // 删除后缀

int main(void) {
    char *strcp=(char*)malloc(1000*sizeof (char));  // 复制字符串
    char *str=(char*)malloc(1000*sizeof (char));  // 原字符串
    char *word=(char*) malloc((1000*sizeof (char)));  // 要删除的前后缀
    scanf(" %[^\n]",str);
    scanf(" %[^\n]",word);
    strcpy(strcp,str);
    deleteprefix(strcp,word);  // 删除前缀
    printf("%s\n",strcp);
    strcpy(strcp,str);
    deletepostfix(strcp,word);  // 删除后缀
    printf("%s",strcp);
    free(strcp);
    strcp=NULL;
    free(str);
    str=NULL;
    free(word);
    word=NULL;
    return 0;
}

void deleteprefix(char *str,char *word){
    int len1= (int)strlen(str);  // 获取字符串和单词的长度
    int len2= (int)strlen(word);
    int flag=1;  // 标记是否存在前缀
    if(str[0]==word[0]){
        for(int i=1;i<len2;i++){
            if(str[i]!=word[i])
                flag=0;
        }
        if(flag==1){  // 存在前缀
            for(int i=0;i<(len1-len2);i++){  // 进行前移
                str[i]=str[i+len2];
            }
            str[len1-len2]='\0';
            deleteprefix(str,word);  // 再次删除前缀
        }
    }
}

void deletepostfix(char *str,char *word){
    int len1= (int)strlen(str);  // 获取字符串和单词的长度
    int len2= (int)strlen(word);
    int flag=1;  // 标记是否存在后缀
    if(str[len1-1]==word[len2-1]){
        for(int i=(len1-2); i>(len1-1-len2); i--){  // 从后往前比较
            if(str[i]!=word[len2-(len1-2-i)-2]){
                flag=0;
                break;
            }
        }
        if(flag==1){  // 存在后缀则截断字符串
            str[len1-len2]='\0';
            deletepostfix(str,word);  // 再次删除后缀
        }
    }
}

思路：因为题目要求输出的是分别删除前缀和后缀的结果，所以需要对原字符串进行复制以保留。然后分别删除前缀和后缀并进行输出。前缀是从前往后相比，后缀是从后往前相比，如果出现完整的要删除内容则前缀前移，后缀截断。然后继续检测是否存在相符合的前缀或后缀，直到没有符合的前缀或后缀。

060 前后缀移除

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

void deleteLeft(char *str,char *sam);  // 从左侧删除
void deleteRight(char *str,char *sam);  // 从右侧删除
int main(void) {
    char *str=(char*)malloc(10000*sizeof (char));  // 原字符串
    char *sam=(char*)malloc(10000*sizeof(char));  // 要删除的字符范围
    char *strcp=(char*)malloc(10000*sizeof(char));  // 复制原字符串
    scanf(" %[^\n] %[^\n]",str,sam); 
    strcpy(strcp,str);
    deleteLeft(strcp,sam);  // 从左侧删除
    printf("%s\n",strcp);
    strcpy(strcp,str);  // 复制字符串
    deleteRight(strcp,sam);  // 从右侧删除
    printf("%s\n",strcp);
    deleteLeft(strcp,sam);  // 再从左侧删除，使得从两侧删除
    printf("%s",strcp);
    free(strcp);
    strcp=NULL;
    free(str);
    str=NULL;
    free(sam);
    sam=NULL;
    return 0;
}
void deleteLeft(char *str,char *sam){
    int len1= strlen(str);  // 获取字符串和要删除的字符范围的长度
    int len2= strlen(sam);
    for(int i=0;i<len1;i++){
        int ctr=0;  // 记录是否有需要删除的字符
        for(int j=0;j<len2;j++){
            if(str[0]==sam[j]){
                ctr=1;
                for(int n=0;n<(len1-1-i);n++){  // 前移
                    str[n]=str[n+1];
                }
                str[len1-i-1]='\0';  // 标志结束
                break;
            }
        }
        if(ctr==0){  // 不存在需要删除的字符则结束
            break;
        }
    }
}
void deleteRight(char *str,char *sam){
    int len1= strlen(str);
    int len2= strlen(sam);
    for(int i=len1-1;i>=0;i--){
        int ctr=0;  // 记录是否有需要删除的字符
        for(int j=0;j<len2;j++){
            if(str[i]==sam[j]){  //截断
                ctr=1;
                str[i]='\0';
                break;
            }
        }
        if(ctr==0){  // 不存在需要删除的字符则结束
            break;
        }
    }
}

题目表意不清：题目的意思是第二个字符串是需要删除的字符范围，如果出现了第二个字符串中的字符则进行删除。也就是是从左侧删除的意思是从左边第一个字符开始判断该字符是否在第二个字符串中，如果在则删除，再继续检验下一个字符是否在第二个字符串中。直到该字符不在这个字符串中。

思路：因为题目要求输出多次，所以需要将原来的字符串进行复制。并且在从右侧删除并输出后，可以紧接着删除左侧字符并输出。

061 【专业融合：电子】Arduino显示

#include <stdio.h>
#include "stdlib.h"

int numToPower(int n);  //获取数字n所需的能量功耗
int total(int n);  // 计算n有多少满足的等式

int main(void) {
    int n;
    scanf(" %d",&n);
    int ans= total(n);
    printf("%d",ans);
    return 0;
}

int numToPower(int n){
    if(n<10){
        switch (n) {  // n为一位数，返回相应的能量功耗
            case 0: return 6;
            case 1: return 2;
            case 2: return 5;
            case 3: return 5;
            case 4: return 4;
            case 5: return 5;
            case 6: return 6;
            case 7: return 3;
            case 8: return 7;
            case 9: return 6;
            default: return 0;
        }
    }
    else{  //n为多位数则每位能量功耗依次相加
        int total = 0;
        while(n){
            total += numToPower(n%10);
            n /= 10;
        }
        return total;
    }
}

int total(int n){
    int ctr = 0;  // 计数有多少满足的等式
    for(int i=0; i<100&&(numToPower(i)<n); i++){  // 枚举
        for(int j=0; j<100&&((numToPower(i)+ numToPower(j))<n); j++){
            int ip=numToPower(i), jp=numToPower(j), tp=numToPower(i+j);
            if((ip+jp+tp+4) == n){  // 总功耗为n
                ctr++;
            }
        }
    }
    return ctr;
}

注意：加数可以为两位数。

思路：首先要能够根据数字得出所需要的功耗。然后枚举数字，并使得加数和结果的总功耗+4为n(加号和等号共占用4个功耗)。

062 【专业融合：通信】GPS通讯协议

#include <stdio.h>
#include <string.h>
#include <math.h>

int main(){
    char str[1000];  // 存储输入的字符串
    while(1){
        int flag=1;  // 判断是否应该处理
        scanf(" %s",str);
        if(strcmp(str,"END")==0)  // 如果输入字符串为END
            break;
        char test[6]="GPRMC";
        for(int i=1;i<6;i++){  // 判断前面是否为GPRMC
            if(str[i]!=test[i-1]){
                flag=0;
                break;
            }
        }
        if(flag==0)  // 如果该行不用处理直接进行下次循环
            continue;
        int res=(int)str[1];  // 为做异或操作做准备
        int n=2;  // 记录*在多少位
        for(int i=2;str[i]!='*';i++){
            res^=str[i];  // 获取每位与下一位的不断异或结果
            n++;
        }
        int res_16=0;  // 结果转化为16进制
        int ctr=0;  // 计数是第几位
        while(res>0){
            res_16+=res%16*(int)pow(10,ctr);
            res/=16;
            ctr++;
        }
        int num=0;
        for(int i=(n+1);str[i]!='\0';i++){  // 获取末尾数字
            num*=10;
            num+=str[i]-'0';
        }
        if(num!=res_16)  // 如果检验值对不上
            printf("error\n");
        else{
            int time_h=0;  // 记录时间小时
            time_h=(str[7]-'0')*10+(str[8]-'0')+8;
            if(time_h>=24)
                time_h%=24;
            if(time_h/10==0)
                printf("0");
            printf("%d:",time_h);
            printf("%c%c:",str[9],str[10]);
            printf("%c%c\n",str[11],str[12]);
        }
    }
    return 0;
}

/*Sample Input
$GPRMC,024813.640,A,3158.4608,N,11848.3737,E,10.05,324.27,150706,A*50
$GPGSV,3,1,11,10,63,137,17,07,61,098,15,05,59,290,20,08,54,157,30*70
$GPRMC,194548.127,A,5230.657,N,01325.713,E,3968.7,122.8,200220,000.0,W*44
$GPGGA,092750.000,5321.6802,N,00630.3372,w,1,8,1.03,61.7,M,55.2,M,*76
$GPRMC,111724.681,A,5231.801,N,01329.267,E,1289.3,000.0,291123,000.0,W*48
$GNVTG,112.99,T,109.99,M,0.15,N,0.08,K,A*3B
END
Sample Output
10:48:13
error
19:17:24*/
/*将“$”和“*”之间所有的字符做运算
（第一个字符和第二个字符异或，结果再和第三个字符异或，依此类推）
之后的值对65536取余后的结果*/

这题是真的太逆天了，样例输入这么长还不让粘贴…

思路：现判断开始的五个字母是否为GPRMC，如果是那么处理。将$和*之间不断异或然后再与最后数字相比较，如果不同输出error，如果相同则将最开始表示时间的6位数字通过小时数加8输出(UTC时间+8为北京时间)，其中需要注意，超过24需要取模，而如果最终小时数为个位数需要先在前面补一个0。

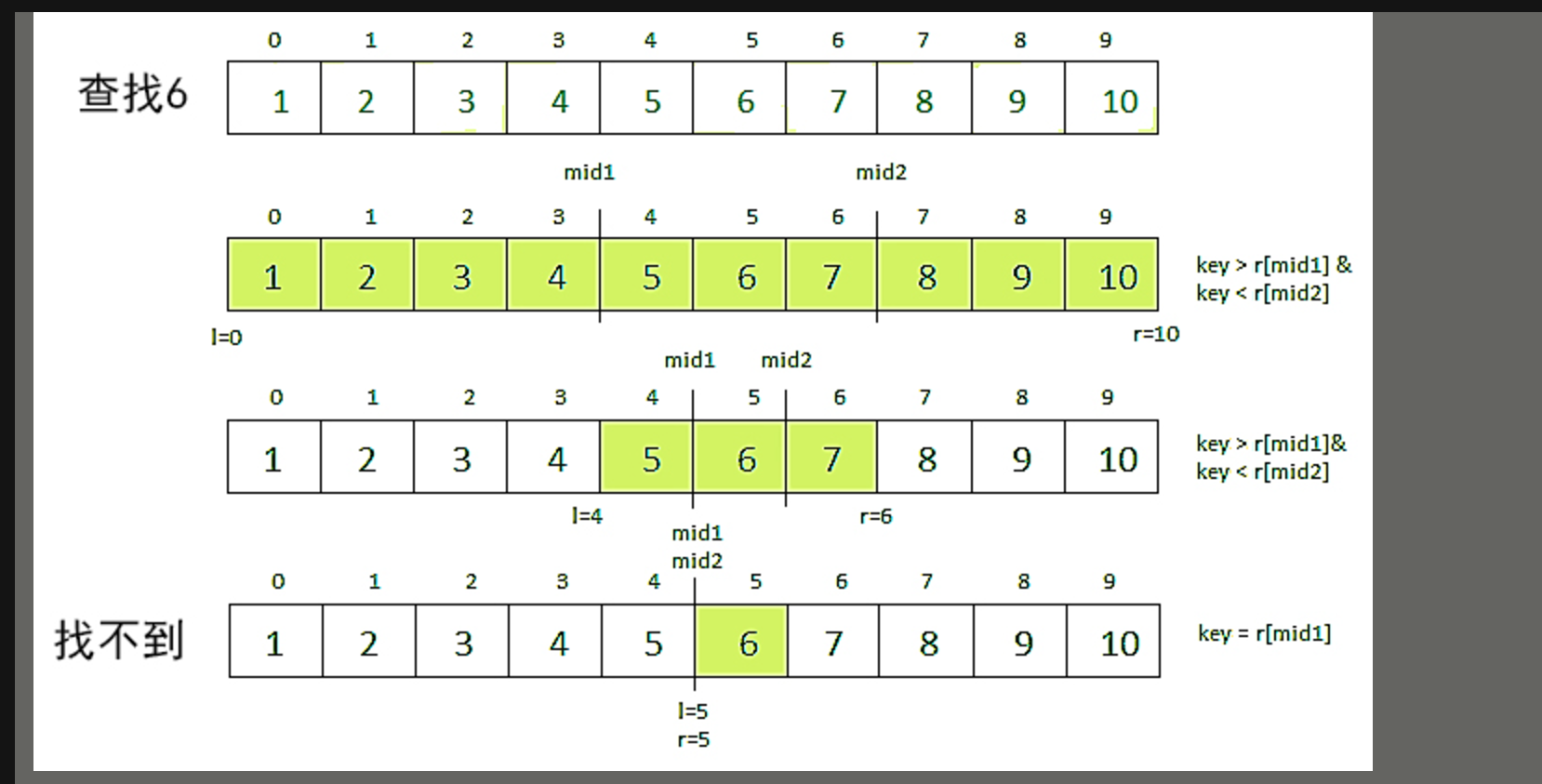
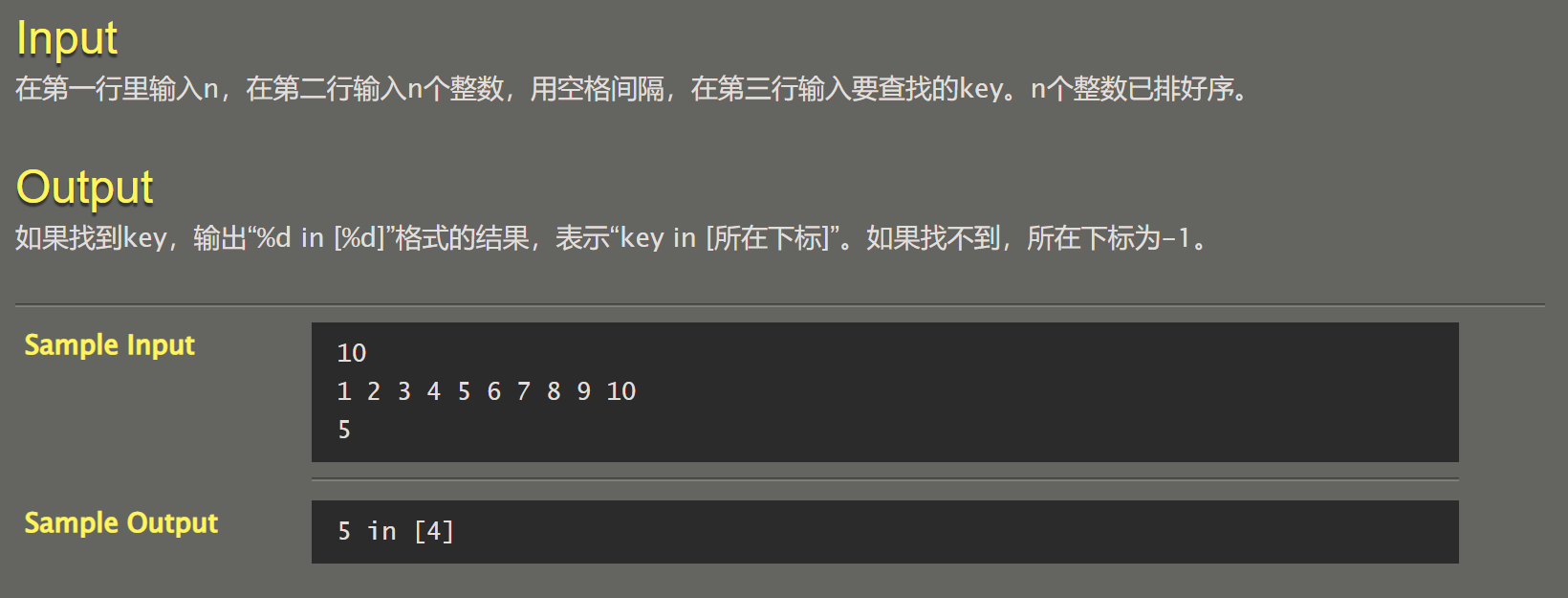
063 三元搜索

#include <stdio.h>
#include "stdlib.h"

int findSubscript(int n,int *sequence,int key,int l,int r);  // 三元搜索目标下标
// l为左边界,r为右边界下标
int main(void) {
    int n;  // 输入的数的个数
    scanf(" %d",&n);
    int *sequenceNumber=(int*)malloc(n*sizeof (int));  // 数字序列
    for(int i=0;i<n;i++)
        scanf(" %d",&sequenceNumber[i]);
    int key;  // 要查找的数字
    scanf(" %d",&key);
    int l=0,r=n-1;
    int ans= findSubscript(n,sequenceNumber,key,l,r);
    printf("%d in [%d]",key,ans);
    free(sequenceNumber);
    sequenceNumber=NULL;
    return 0;
}

int findSubscript(int n,int *sequence,int key,int l,int r){
    int mid1=l+(r-l)/3, mid2=r-(r-l)*1/3, ans=0;  // 将目标区域分为三份
    // 如果两个下标中有一个符合目标则结束
    if(sequence[mid1]==key)
        return mid1;
    else if(sequence[mid2]==key)
        return mid2;
    else if((key<sequence[mid1])&&(mid1<mid2)){  // 如果目标在最左部分
        r=mid1-1;  // 调整右边界
        return findSubscript(n,sequence,key,l,r);  // 使用新调整的边界进行搜索
    }
    else if((key>sequence[mid2])&&(mid1<mid2)){  // 如果目标在最右部分
        l=mid2+1;  // 调整左边界
        return findSubscript(n,sequence,key,l,r);
    }
    else{  // 如果目标在中间
        if((mid2-mid1==1)||(mid1-mid2==1)||(mid1==mid2)){  // 如果此时中间已经没有空隙，那么找不到
            return -1;
        }
        else{  // 中间有空隙,调整左右边界，继续搜索
            l=mid1+1;
            r=mid2-1;
            return findSubscript(n,sequence,key,l,r);
        }
    }
}

思路：将目标区域分为三份，搜索目标在哪份中，如果在最左份中，那么将右边界进行调整为第一个三等分-1。如果在最右份，那么调整左边界为第二个三等分+1。如果在中间，则调整边界到中间范围内。

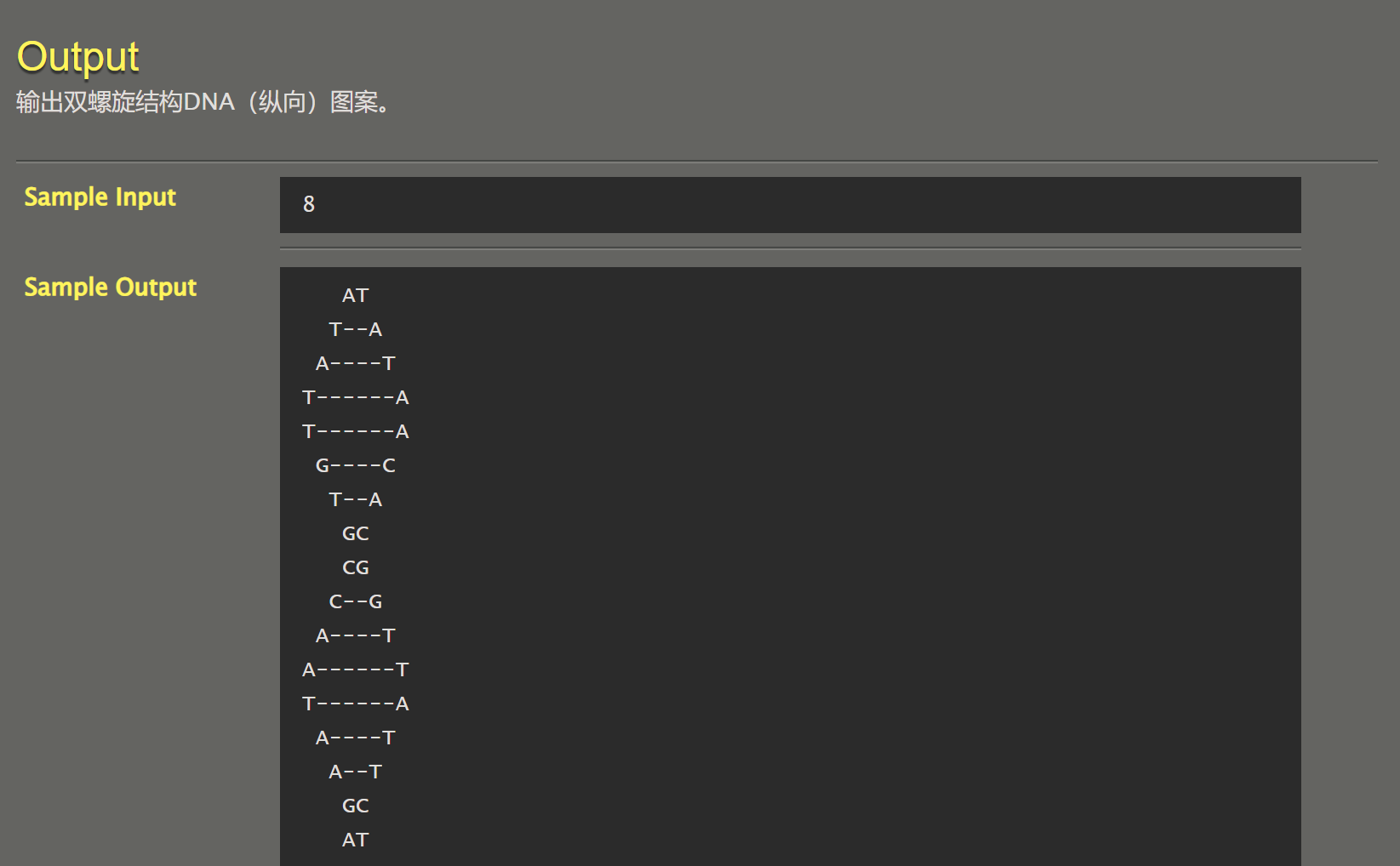
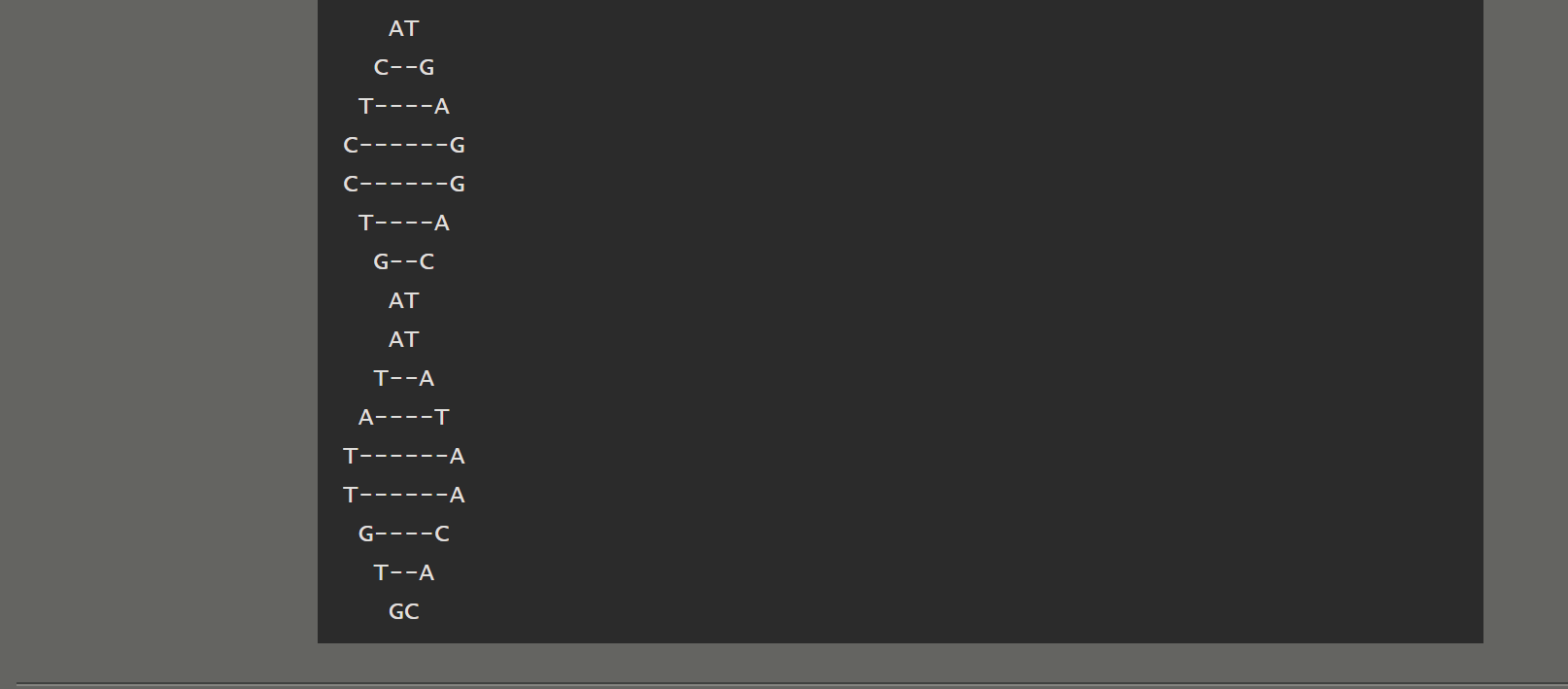
064 【专业融合：生物】DNA双螺旋结构

#include <stdio.h>

void putDNA(int n);  // 打印相应的DNA序列

int main(void) {
    int n;  // 上下叶的数量
    scanf(" %d",&n);
    for(int i=1;i<=n;i++){
        if((i%6)==0)  // 如果i刚好为6的整数倍
            putDNA(6);
        else putDNA(i%6);  // 对6取余打印DNA序列，因为每6个一个循环
    }
    return 0;
}

void putDNA(int n){
    switch (n) {
        case 1:{
            printf("   AT\n  T--A\n A----T\nT------A\n");
            break;
        }
        case 2:{
            printf("T------A\n G----C\n  T--A\n   GC\n");
            break;
        }
        case 3:{
            printf("   CG\n  C--G\n A----T\nA------T\n");
            break;
        }
        case 4:{
            printf("T------A\n A----T\n  A--T\n   GC\n");
            break;
        }
        case 5:{
            printf("   AT\n  C--G\n T----A\nC------G\n");
            break;
        }
        case 6:{
            printf("C------G\n T----A\n  G--C\n   AT\n");
        }
    }
}

这题有点意义不明的感觉，直接设一个函数，其中设置6个printf()函数，然后从1到n对6取余(但是如果是6的倍数的话，需要传入6)依次调用这个函数就好。

065【专业融合：自动化】PID控制

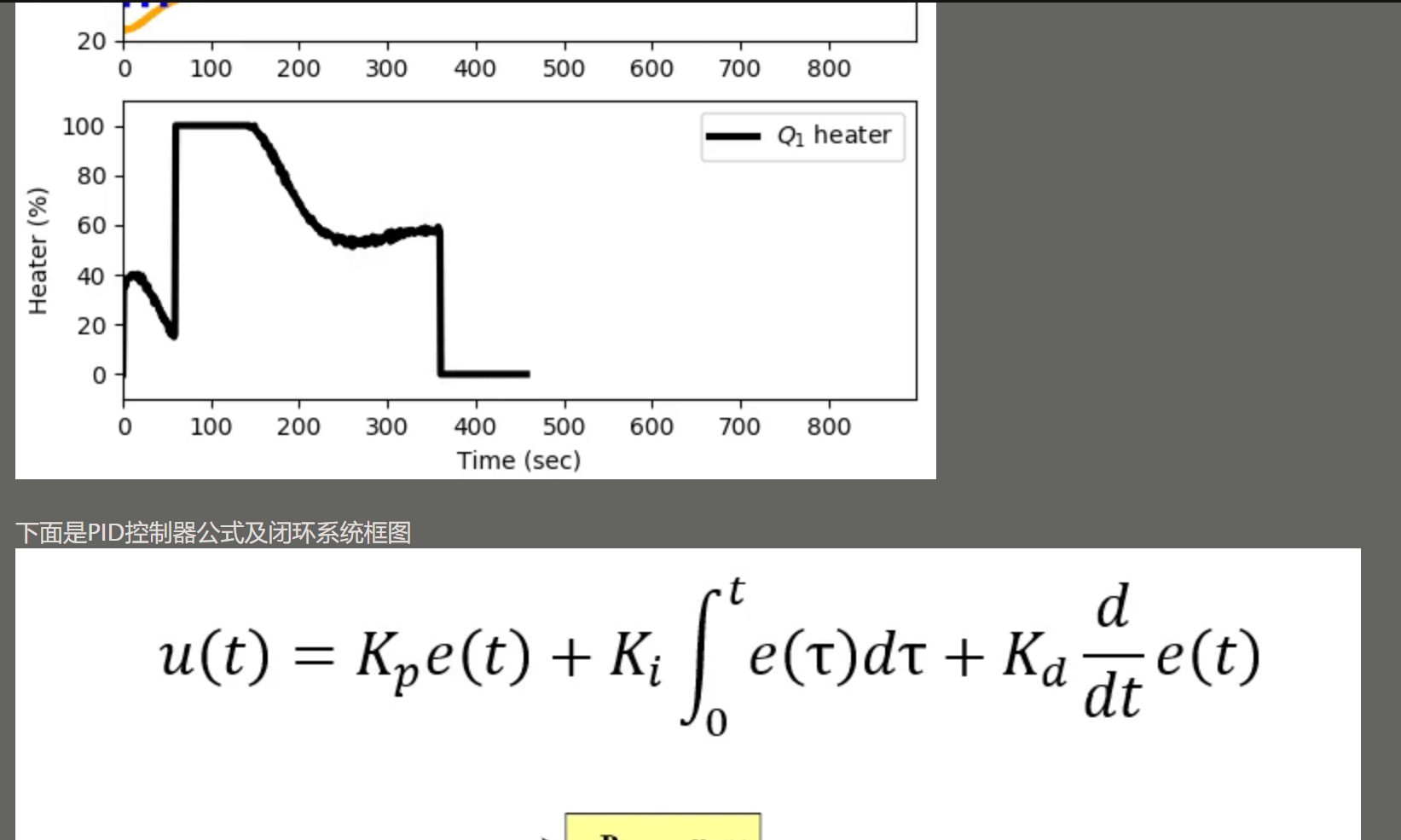
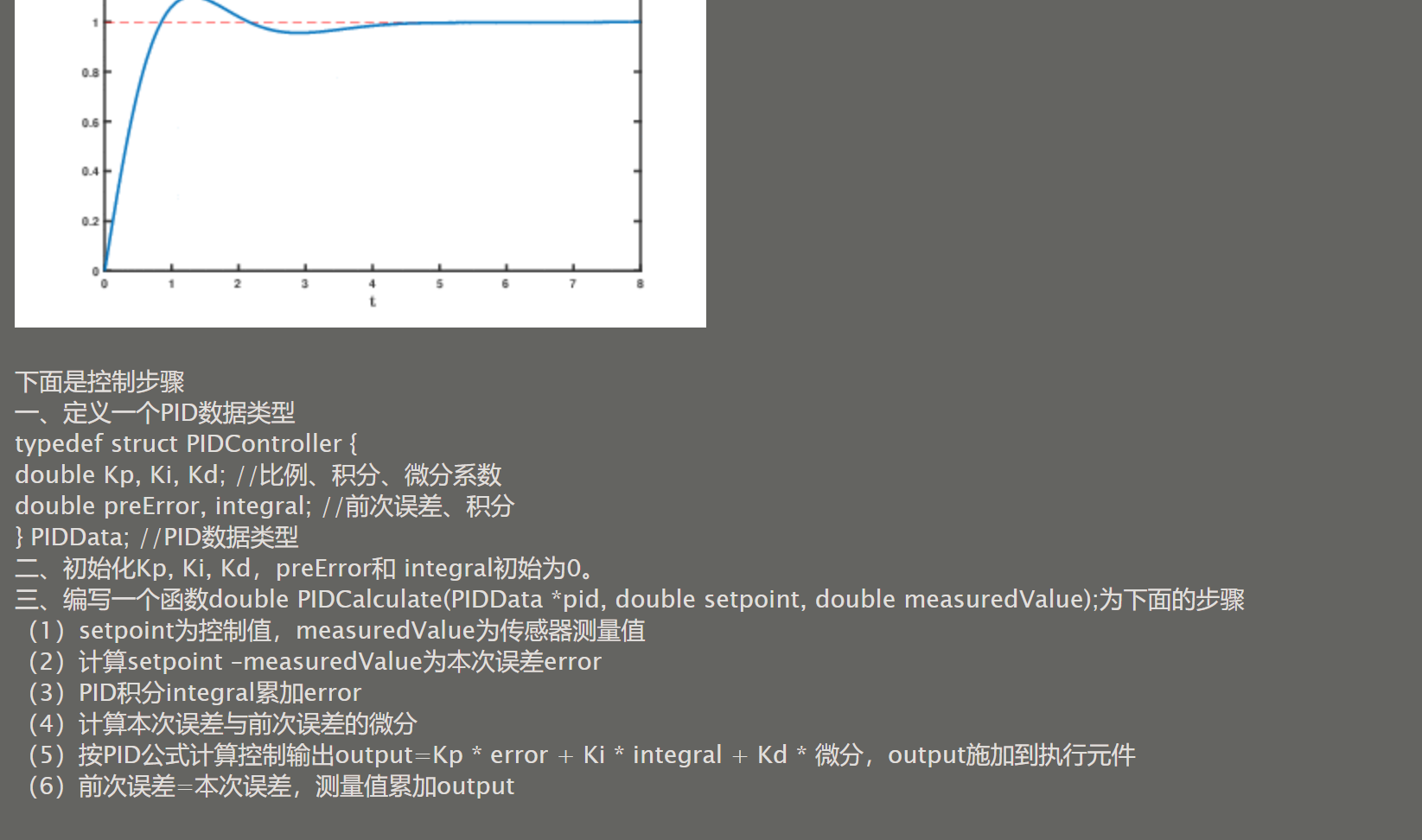
#include "stdio.h"
#include "stdlib.h"

typedef struct PIDController{//按题目写就行
    double Kp,Ki,Kd;//比例，积分，微分系数
    double preError,integral;//前次误差，积分
}PIDDate;
void initial_structure(PIDDate *p);
double PID_calculate(PIDDate *p,double setPoint,double measureValue);
int main(){
    PIDDate *pid=(PIDDate*) malloc(sizeof (PIDDate));//设置结构体指针
    double setPoint,measuredValue,Kp,Ki,Kd;//控制值，测量值,比例，积分，微分系数，注意后三个不是整数。
    int n;
    initial_structure(pid);
    scanf(" %lf %lf %lf %lf %lf %d",&pid->Kp,&pid->Ki,&pid->Kd,&setPoint,&measuredValue,&n);
    for(int i=1;i<=n;i++){
        double output= PID_calculate(pid,setPoint,measuredValue);
        measuredValue+=output;//题目输出错误，输出为测量值了
        printf("%d %.6lf\n",i,measuredValue);
    }
    free(pid);
    pid=NULL;
}
void initial_structure(PIDDate *p){//其实只需要给preError和integral初值0就行
    if(p==NULL)
        exit(1);
    p->preError=0;
    p->integral=0;
}
double PID_calculate(PIDDate *p,double setPoint,double measureValue){
    //按照题目所给步骤计算
    if(p==NULL)
        exit(1);
    double error=setPoint-measureValue;
    p->integral+=error;
    double difference=error-p->preError;//题目有误，应该是计算差值
    double output=p->Kp*error+p->Ki*p->integral+p->Kd*difference;
    p->preError=error;
    return output;
}

题目输出样例输出错误：题目说要输出控制输出output，但样例上输出的却是测量值measuredValue。

题目步骤解释有误：题目第4步说计算微分，实际上应该是计算本次误差与前次误差的差值,以及Kp,Ki,Kd均不是整数。

题目解释不清：题目说总时间和时间点，但没有说计算一次算经过一个时间点。

思路：按照题目所说写出设置结构体参数。赋初值0。然后按题目步骤写出函数，每计算一次输出一次即可。

066 有效表达式

#include "stdio.h"

int main(){
    int n,ans=1;
    scanf(" %d",&n);//套用卡特兰数公式计算即可
    for(int i=(n+2);i<=2*n;i++)
        ans*=i;
    for(int i=1;i<=n;i++)
        ans/=i;
    printf("%d",ans);
    return 0;
}

思路：
$$\begin{gathered} 这题本质上是卡特兰数的应用，具体的变形和应用及各类递推公式可以自行搜索，这里只讲这题的思路。 \\ 这题有n对括号()需要组合，其中n个左括号(对应n个右括号)。 \\ 以三对括号为例,(()))(这样是不可以的，因为其中有一个左括号无法找到与之相配的右括号 \\ 可以将左右括号抽象为+1和-1，上面这个可以写作+1+1-1-1-1+1(序列一)的形式 \\ 若将其从左往右相加，则在第五个-1处相加的结果为-1， \\ 代表着右括号之前没有与之相应的左括号，即在其左边缺少一个+1。 \\ 可称这样的序列为非法序列,而每个非法序列必然在从左往右相加的过程中出现-1的中间量 \\ 我们可将此类非法序列从第一个直到加法结果为-1的第n个进行取相反数,像上面那个序列， \\ 反转后为:-1-1+1+1+1+1(序列二)，容易发现这两个序列存在着一一对应关系。 \\ 一个非法序列一只可能对应一个序列二，而每个序列二也对应着一个非法序列一。 \\ 为什么说序列二对应的序列一均为非法呢? \\ 注意，序列二有着4个+1，2个-1，将序列二从左往右相加必然其中能够得到+1(可能一直加到最后一个) \\ 假设一直加到第n个数取到+1，那么将之前包括第n个数取相反数 \\ 这n个数中+1的个数与-1的个数会发生交换，即是+1减少一个，-1增加一个 \\ 那么整个序列又会拥有3个+1，3个-1。而从左往右加到第n个数 \\ 会得到-1(因为序列二前n个数取了相反数)，那么这个序列则是非法序列。 \\ 让我们将其从3对括号扩展为n对括号，即是有n个+1和n个-1，那么我们只需要找到非法序列所对应的序列二 \\ 即可找到非法序列，而序列二拥有着n+1个+1和n-1个-1。那么这种序列二有多少个呢? \\ 可以想象总共有2n个空需要填充+1或-1 \\ 2n个 \\ \overbrace{[][][][][][]\cdot \cdot \cdot [][][][][][][]} \\ 这其中n+1个空填充+1，而+1填充完之后-1的位置就确定下来了 \\ 而+1填充方法共有C_{2n}^{n+1}个(2n个空中选n+1个空进行填充) \\ 所以序列二的个数就是C_{2n}^{n+1}个，序列一的个数因为一一对应，所以相同。 \\ 而总共有多少种序列呢? \\ 也可以想象为填空位，是2n个空格中填n个+1，n个-1，那么总共有C_{2n}^n种序列 \\ 因此可以得到结果，有效序列共有C_{2n}^n-C_{2n}^{n+1}种 \\ 展开后为\frac{(2n)!}{n!\cdot n!}-\frac{(2n)!}{(n+1)!\cdot (n-1)!} \\ 整理得到\frac{(2n)!}{n!\cdot n!}\cdot (1-\frac{n}{n+1}) \\ 则最终结果为\frac{C_{2n}^n}{n+1} \\ 计算时可以将其展开，为\frac{(2n)!}{n!\cdot n!\cdot (n+1)} \\ 上下约分后得到\frac{2n\cdot (2n-1)\cdot \cdot \cdot (n+3)\cdot (n+2)}{n!}，这就是代码计算原理 \end{gathered}$$
本题考查组合数知识中的卡特兰数，有兴趣的同学可以自行查阅相关知识。我上文给出的只是一种我认为较为容易理解的一种方法，有关卡特兰数的其他推导方法可以自行查找。

067 【专业融合：建筑】长安

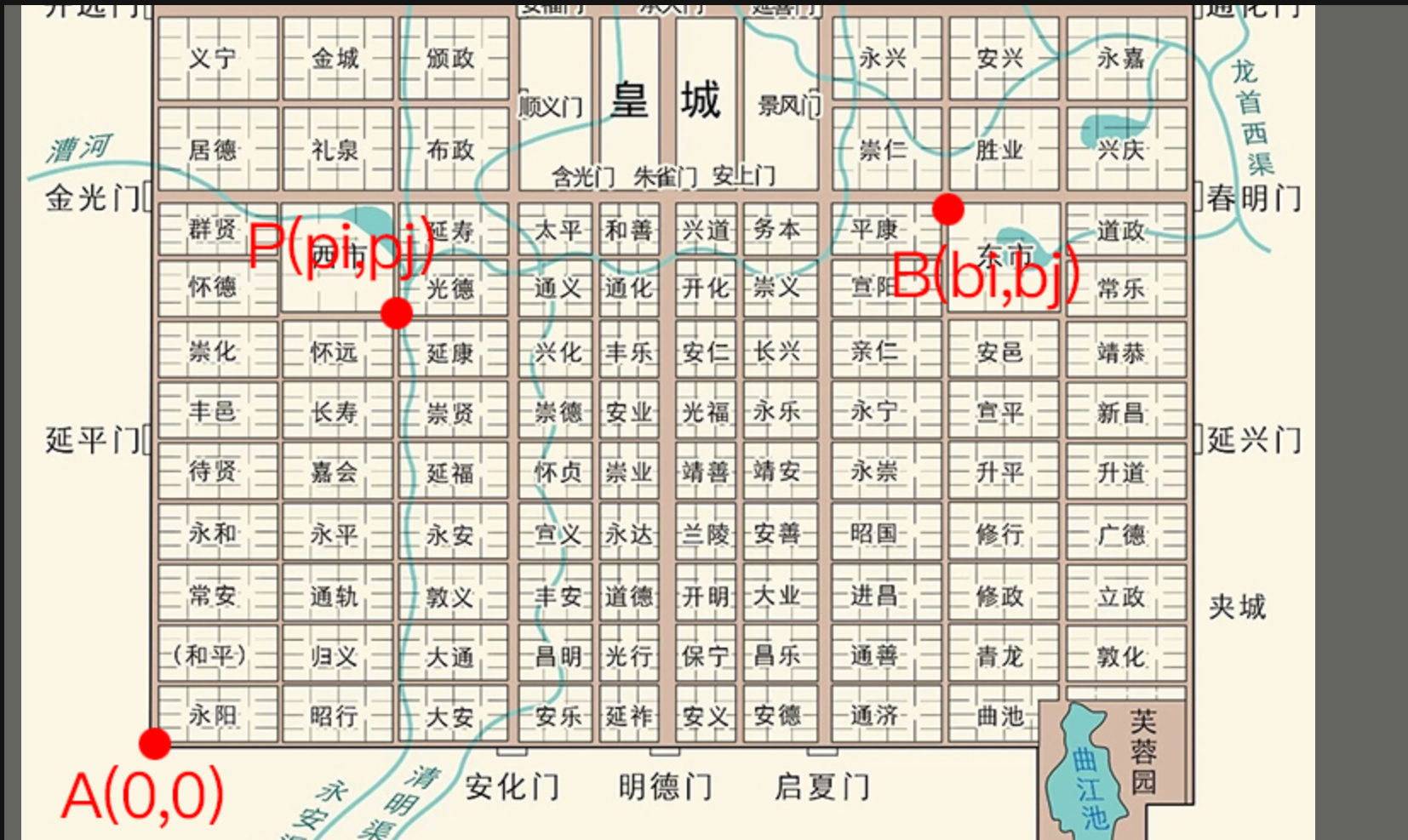
#include "stdio.h"
#include "stdlib.h"
#define min(x,y) ((x)<(y)?(x):(y))

int getSort(int *p);//获取有多少中可嫩

int main(){
    int **coordinate=(int**)malloc(sizeof (int*));//记录坐标
    if(coordinate==NULL)//若是分配失败
        exit(1);
    int **temps;//中间量，传递地址
    int n=0,flag=1;//n用于记录这是第(n+1)行坐标，flag用于判断是否应该结束
    while (1){
        if(n>0){
            temps=(int**) realloc(coordinate,(n+1)*sizeof (int*));
            if(temps==NULL){//若是realloc堆分配失败
                for(int i=0;i<n;i++){
                    free(coordinate[i]);
                    coordinate[i]=NULL;
                }
                exit(1);
            }
            coordinate=temps;//给coordinate分配新内存空间
            temps=NULL;
        }
        coordinate[n]=(int*) malloc(4*sizeof(int) );
        for(int i=0;i<4;i++)
            scanf(" %d",&coordinate[n][i]);//接收坐标
        for (int i = 0; i < 4; ++i) {
            if(coordinate[n][i]<=0){//判断坐标是否存在小于或等于0的情况
                flag=0;
                break;
            }
        }
        if(flag==0)
            break;
        n++;
    }
    for(int i=0;i<n;i++){
        printf("%d\n", getSort(coordinate[i]));
    }
    //释放堆并赋值
    for(int i=0;i<=n;i++){
        free(coordinate[i]);
        coordinate[i]=NULL;
    }
    free(coordinate);
    coordinate=NULL;
    return 0;
}

int getSort(int *p){
    if((p[2]==p[0])&&(p[3]==p[1]))//先考虑P点与B点重合情况
        return 0;
    int baseB=1,minusP=1;
    //先不考虑P点计算总可能数
    for(int j=p[0]+p[1]-2;j>=(p[0]+p[1]-2-min(p[0],p[1])+2);j--){
        baseB*=j;
    }
    for(int j=2;j<=min(p[0],p[1])-1;j++){
        baseB/=j;
    }
    if((p[2]>p[0])||(p[3]>p[1]))//考虑P点在路线外
        return baseB;
    for(int j=p[2]+p[3]-2;j>=(p[2]+p[3]-2-min(p[2],p[3])+2);j--)
        minusP*=j;
    for(int j=2;j<=min(p[2],p[3])-1;j++)
        minusP/=j;
    int x=p[0]-p[2],y=p[1]-p[3];
    for(int j=x+y;j>=x+y-min(x,y)+1;j--)
        minusP*=j;
    for(int j=2;j<=min(x,y);j++)
        minusP/=j;
    return baseB-minusP;//返回总可能性
}

题目图片错误：起点坐标为(1,1)而不是(0,0)。

思路：
$$\begin{gathered} 先说如何计算从A(x_1,y_1)到B(x_2,y_2)有多少种可能性: \\ 此时共需沿着x轴走x_2-x_1步，再沿着y轴走y_2-y_1步。 \\ 把向右一步走用\to 表示，向上一步走用\uparrow 表示 \\ 那么方案可看作(x_2-x_1)个\to 和(y_2-y_1)个\uparrow 的排列组合。 \\ 可以抽象为有(x_2-x_1)+(y_2-y_1)个空格，将\to 和\uparrow 填入 \\ (x_2-x_1)+(y_2-y_1)个 \\ \overbrace{[][][][][][]\cdot \cdot \cdot [][][][][]} \\ 我们可以先将\to 和\uparrow 中较少的填入以方便计算，但一个箭头填完后 \\ 另外一个箭头的位置就确定了。 \\ 若此时(x_1-x_2)较少，那么填入的方案有C_{(x_2-x_1)+(y_2-y_1)}^{(x_1-x_2)}种 \\ 那么此题就可以用此方法解决: \\ 先确定A到B有多少种方案，再减去从A经P再到B的方案数，便是结果 \\ 求从A经P再到B的方案数需要依次求出从A到P的方案数，再求出从P到B的方案数，最后两个方案数相乘 \\ 至于组合数的计算，便不再继续赘述。 \end{gathered}$$

068 时钟A-B

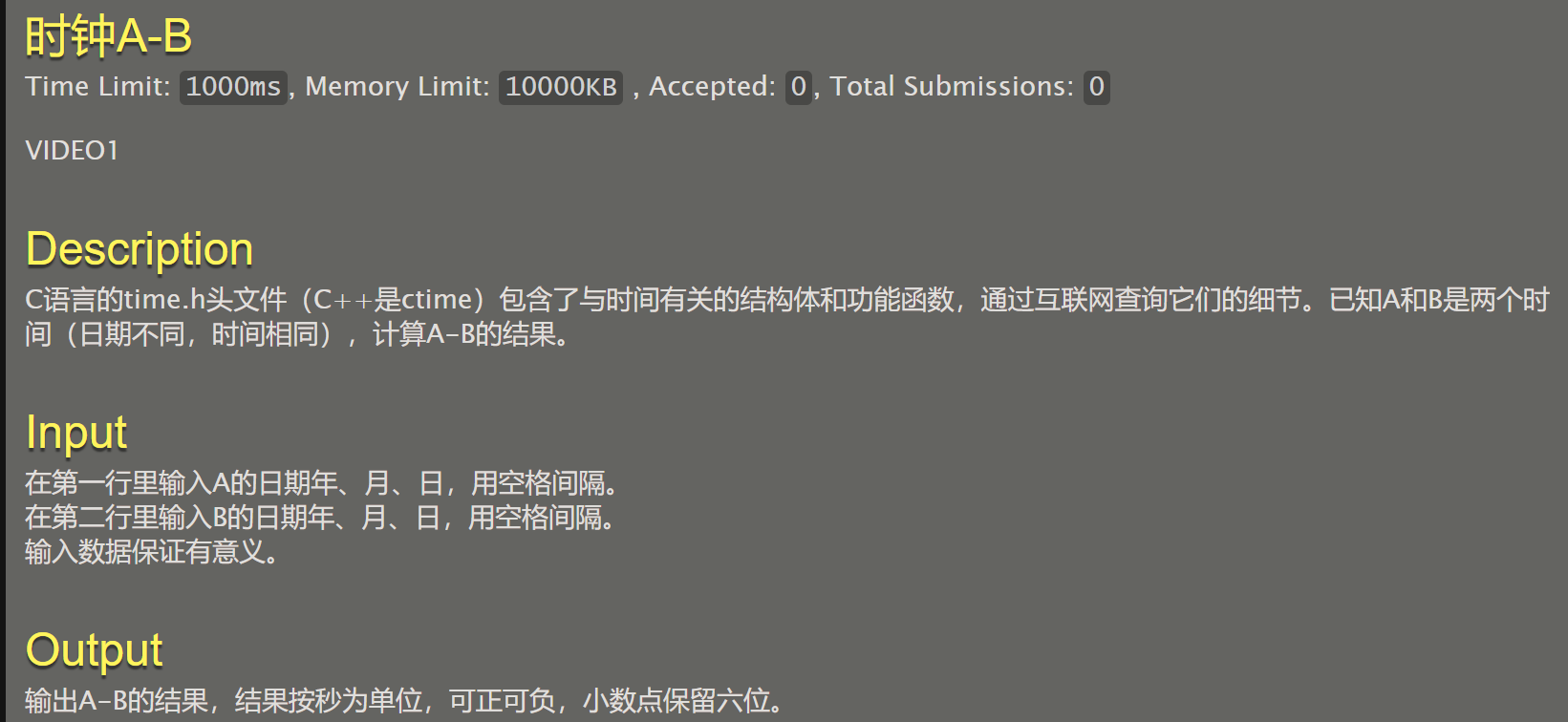
#include "stdio.h"
#include "time.h"

int main(){
    int aY,aM,aD,bY,bM,bD;
    scanf(" %d %d %d %d %d %d",&aY,&aM,&aD,&bY,&bM,&bD);
    struct tm timeA;
    struct tm timeB;
    timeA.tm_year=aY-1900;
    timeA.tm_mon=aM;
    timeA.tm_mday=aD;
    timeA.tm_hour=0;
    timeA.tm_min=0;
    timeA.tm_sec=0;
    timeA.tm_isdst=-1;
    timeB.tm_year=bY-1900;
    timeB.tm_mon=bM;
    timeB.tm_mday=bD;
    timeB.tm_hour=0;
    timeB.tm_min=0;
    timeB.tm_sec=0;
    timeB.tm_isdst=-1;
    double  a=(double )mktime(&timeA);
    double b=(double )mktime(&timeB);
    printf("%.6lf",a-b);
    return 0;
}

注意：时间year是从1900开始计算的，所以要减去它。

结构体tm定义：

struct tm {
   int tm_sec;         /* 秒，范围从 0 到 59        */
   int tm_min;         /* 分，范围从 0 到 59        */
   int tm_hour;        /* 小时，范围从 0 到 23        */
   int tm_mday;        /* 一月中的第几天，范围从 1 到 31    */
   int tm_mon;         /* 月，范围从 0 到 11        */
   int tm_year;        /* 自 1900 年起的年数        */
   int tm_wday;        /* 一周中的第几天，范围从 0 到 6    */
   int tm_yday;        /* 一年中的第几天，范围从 0 到 365    */
   int tm_isdst;       /* 夏令时                */
};

mktime()函数声明

time_t mktime(struct tm *timeptr)
把 timeptr 所指向的结构转换为一个依据本地时区的 time_t 值。

其中time_t类型和long long相同。

069 循环排序

#include "stdio.h"
#include "stdlib.h"

int main(){
    int n;
    scanf(" %d",&n);
    int *number=(int*)malloc(n*sizeof (int));
    for(int i=0;i<n;i++)
        scanf(" %d",&number[i]);
    for(int i=0;i<n-1;i++){
        int item=number[i],pos=i;//标记当前需要排的数字和位置
        for(int j=i+1;j<n;j++){//遍历数组，查找位置
            if(number[j]<item)
                pos++;//判断当前数字应该往后移动几位
        }
        printf("item=%d i=%d %d\n",item,i,number[i]);
        if(pos==i)
            continue;//若这个数字已经排好，进入下一次循环
        int temps=number[pos];//让数字排在正确位置
        number[pos]=item;
        item=temps;
        while(pos!=i){
            pos=i;//记录现在需要排序的数字是第几位
            for(int j=i+1;j<n;j++){//遍历数组，查找位置
                if(number[j]<item)
                    pos++;//判断当前数字应该往后排几位
            }
            while(item==number[pos])//如果这个位置已经有了同样的数字
                pos++;
            printf("pos%d\n",pos);
            temps=number[pos];//让数字排在正确位置
            number[pos]=item;
            item=temps;
        }
    }
    for(int i=0;i<n;i++){
        printf("%d ",number[i]);
    }
    free(number);
    number=NULL;
    return 0;
}

注意：这题虽然考查循环排序，但实质上使用任何排序方式均可AC,不过个人认为还是有必要进行了解循环排序的原理和代码实现的。

原理：
$$\begin{gathered} 以样例序列1839101024为例 \\ 从第一个数1开始往后看，发现没有比1更小的数，那么1的位置是正确的 \\ 接下来看第二个数8，从8开始往后看，发现有324这三个数比8小，那么8应该往后移三位 \\ 或者说从第二位往后移三位后的那个位置需要有一个8，因为有三个数可以放在8前面 \\ 然后把那个位置的10和8相互交换，得到新序列1103981024 \\ 那么第二位现在为10了，10的位置对吗? \\ 可以从第二位往后面看，发现有39824五个数少于10，即可以放在10前面。 \\ 那么让我们把10往后移动五位，和那地方的2交换位置。 \\ 序列变为1239810104。此时看交换过来的2位置是否正确。 \\ 往后看，发现没有比2小的数，那么2位置是正确的 \\ 继续看第三个数字，发现也是正确 \\ 第四个数字9，发现后面有84两个数字小于它，所以应该把它往后移动两位，和10交换位置 \\ 新序列为:1231089104再看交换过来的10位置是否正确 \\ 发现后面有894三个数小于它，所以本应将它往后移动三位，但是发现那个位置已经有10了 \\ 怎么办呢？可以将其再往后放，就是与4交换位置。 \\ 得到新序列1234891010，然后再检查第四位，第五位，一直到倒数第二位位置是否正确 \\ 因为只要前面都正确，那么最后一位必然位置正确 \\ 这便是循环排序的原理，依次检验当前位置的数字是否在正确位置，不在则将其排在正确位置 \\ 并与那个位置的数进行交换，再看交换过后，当前位置数字是否正确，不正确则继续交换 \\ 直到当前位置为正确数字，才能移动到下一位检验。 \end{gathered}$$

我这段代码按照题目设了一个item，充当缓冲区的作用。其实不设这个item直接交换数字也可以。

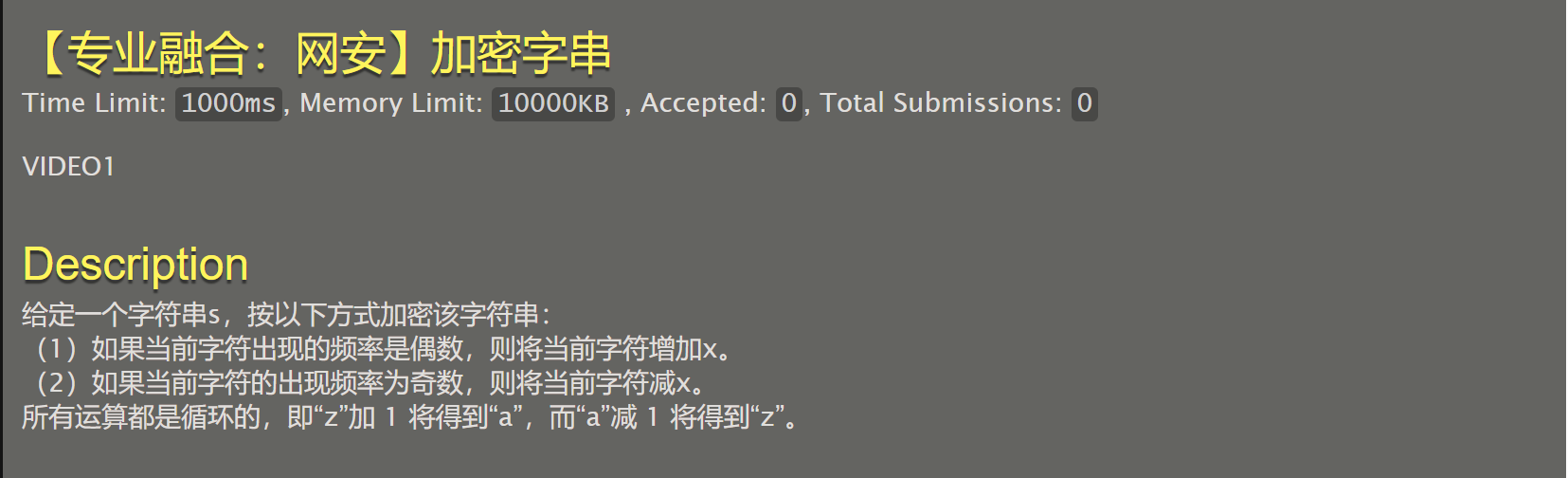
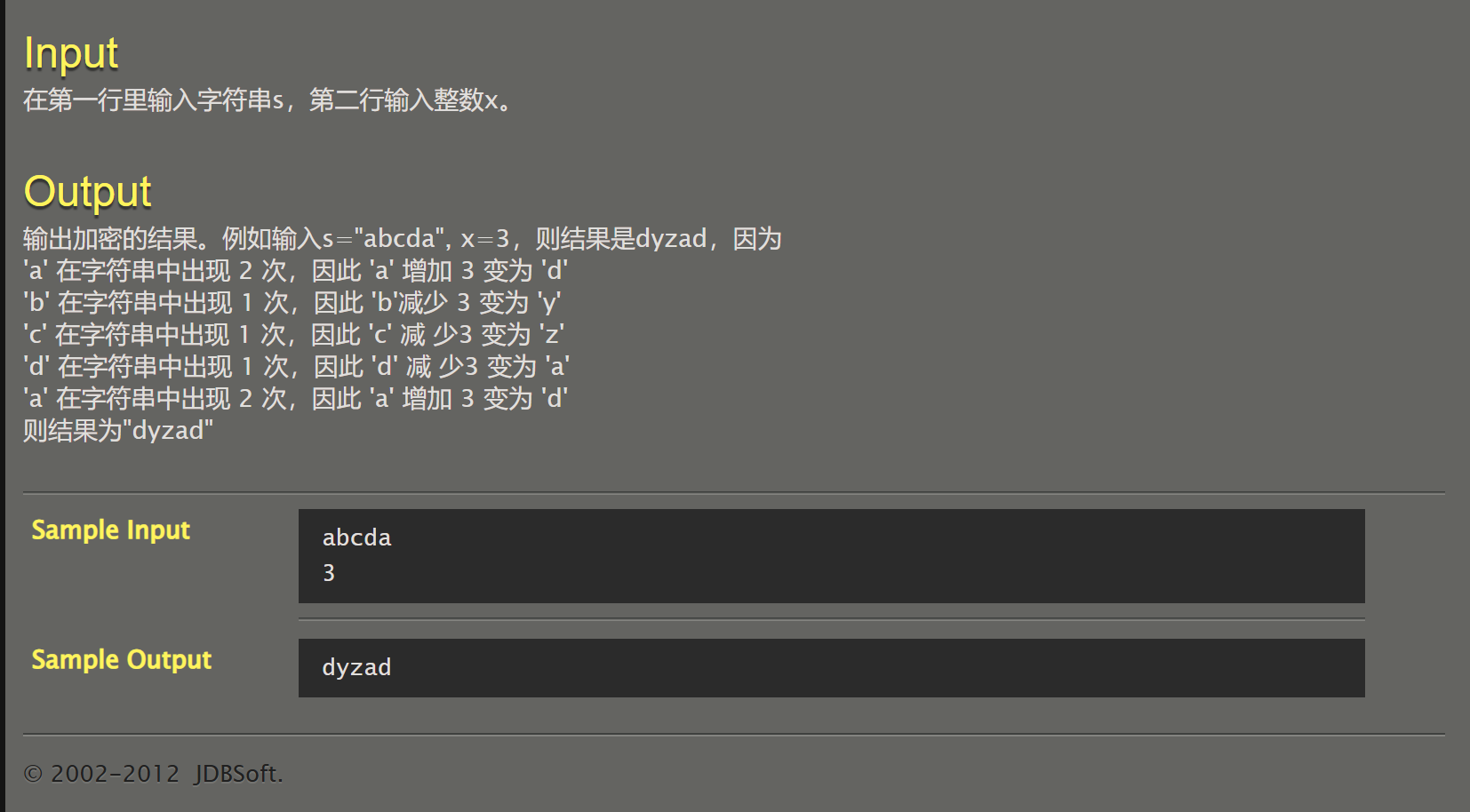
070【专业融合：网安】加密字串

#include "stdio.h"
#include "stdlib.h"
#include "string.h"
void encrypt(char *code,int n);

int main(){
    char *code=(char*) malloc(100*sizeof (char));//密码
    int n;
    scanf(" %s %d",code,&n);
    encrypt(code,n);//密码加密
    printf("%s",code);
    //释放堆，并置NULL
    free(code);
    code=NULL;
    return 0;
}

void encrypt(char *code,int n){
    if(code==NULL){
        exit(1);
    }
    char letters[100];//记录出现的字母
    for(int i=0;i<100;i++)
        letters[i]='\0';//初始化字符串
    char num[100];//记录相应出现的次数
    int number=0;//记录共出现了多少字母
    int len=(int)strlen(code);
    for(int i=0;i<len;i++){
        int flag=0;//用来判断字母是否出现过
        for(int j=0;j<i;j++){
            if(letters[j]==code[i]){//如果该字母出现过
                num[j]++;
                flag=1;
                break;
            }
        }
        if(flag==0){
            //printf("%c\n",code[i]);
            letters[number]=code[i];
            num[number]=1;
            number++;
        }
    }
    char cpy_code[100];//现将加密密码储存在这里，防止影响检测
    cpy_code[len]='\0';
    for(int i=0;i<number;i++){//每个字母依次相加
        if(num[i]%2==0){//如果该字母出现次数为偶数次
            for(int j=i;j<len;j++){
                if(letters[i]==code[j])
                    cpy_code[j]=(code[j]-97+n)%26+97;
            }
        }
        else{
            for(int j=i;j<len;j++){
                if(letters[i]==code[j]){
                    cpy_code[j]=(code[j]-97-n)%26;
                    if(cpy_code[j]>=0)
                        cpy_code[j]+=97;
                    else
                        cpy_code[j]+=26+97;
                }
            }
        }
    }
    for(int i=0;i<len;i++)
        code[i]=cpy_code[i];
}

注意：不要直接对原字符串进行修改操作，要建立一个新字符串存储加密后的密码。因为对原字符串的修改会影响后面的检测步骤。

思路：建立一个字符串和一个整数数组，分别储存有哪些字母以及分别出现了几次（方法为遍历原码字符串，如果发现新字母则储存在这个新建立的字符串中，并把整数数组对应位置赋值1；若这个字母出现过，则在整数数组对应数字加一）。然后遍历字符串，加密后存储在新字符串（建立一个新的字符串存储加密后数据）中，最后让原字符串各位与新字符串相同。

071【专业融合：机械】几何约束

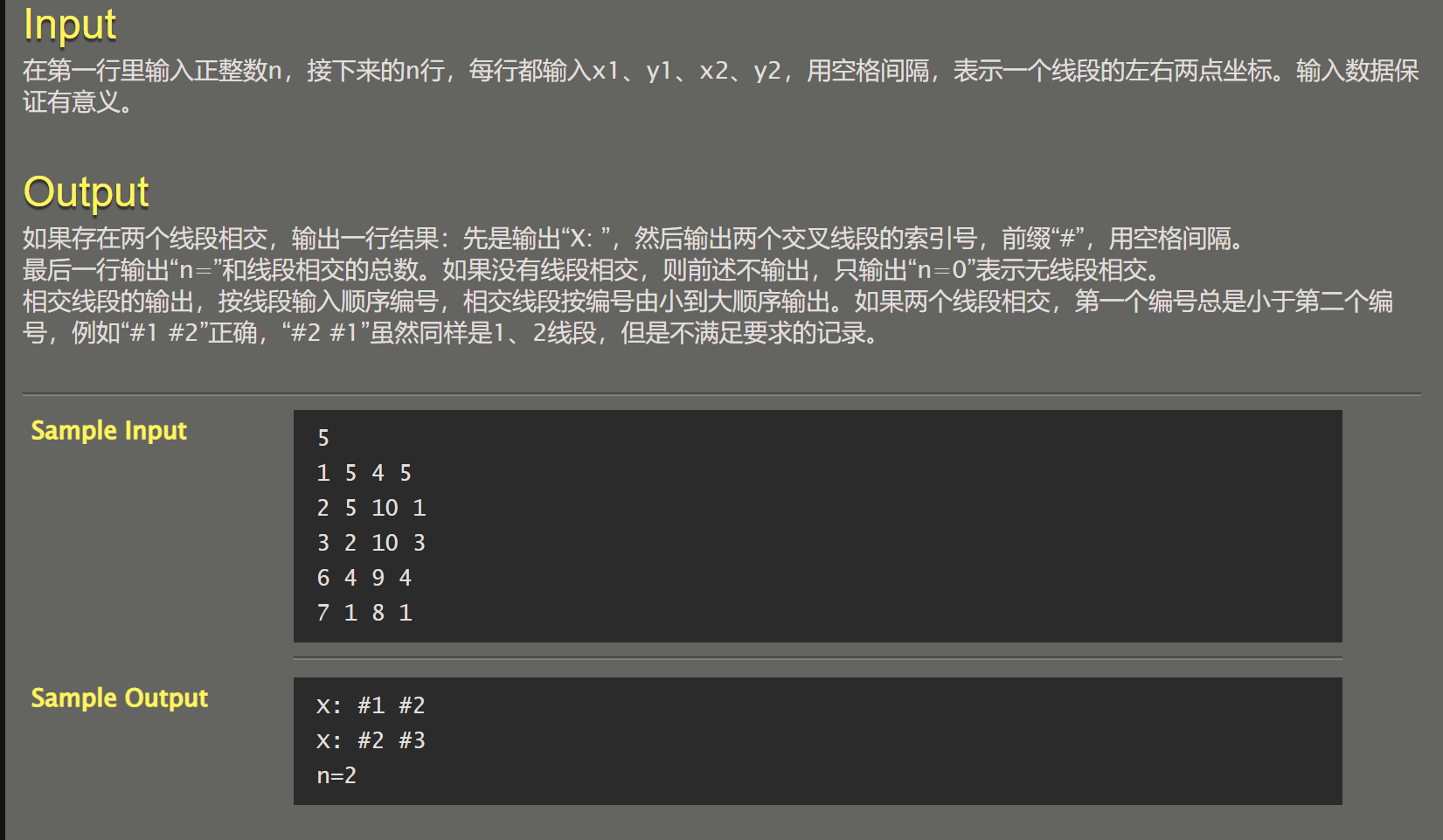
#include <stdio.h>
#include "stdlib.h"
#define min(a,b) ((a<b)?(a):(b))
#define max(a,b) ((a>b)?(a):(b))

int firstCheck(int *p1,int *p2);//初始检测，判断是否可能相交
int specialCheck(int *p1,int *p2);//特殊情况，例如共线的判断
int generalCheck(int *p1,int *p2);//一般情况的检测
int findStart(int *p);//查找两坐标中的初始坐标
int findEnd(int *p);//查找两坐标中的末尾坐标
int crossProduct(int *p);//计算叉乘结果的z的正负

int main(void) {
    int n,**coordinate,check,ctr=0,**ans;
    scanf(" %d",&n);
    coordinate=(int**) malloc(n*sizeof (int*));
    ans=(int**) malloc(n*sizeof (int*));
    for(int i=0;i<n;i++){
        ans[i]=(int*) malloc(2*sizeof (int));//给指向最后答案的指针分配足够的堆
        coordinate[i]=(int*) malloc(4*sizeof (int));//给指向坐标的指针分配堆
        for(int j=0;j<4;j++)
            scanf("%d",&coordinate[i][j]);//读取坐标数据
    }
    for(int i=0;i<n;i++){
        for(int j=(i+1);j<n;j++){
            if(firstCheck(coordinate[i],coordinate[j])==0)
                continue;//最基本的检测，不过直接进行下次循环
            check=specialCheck(coordinate[i],coordinate[j]);
            if(check==-1)//此时共线，但不相交
                continue;
            else if(check==1){//此时共线并相交
                ans[ctr][0]=i;
                ans[ctr][1]=j;
                ctr++;
                continue;
            }
            else{//不共线的情况
                if(generalCheck(coordinate[i],coordinate[j])==1){
                    ans[ctr][0]=i;//若是相交则记录此时是哪两个线段
                    ans[ctr][1]=j;
                    ctr++;
                    continue;
                }
                else continue;
            }
        }
    }
    for(int i=0;i<ctr;i++)
        printf("X: #%d #%d\n",ans[i][0]+1,ans[i][1]+1);
    printf("n=%d",ctr);
    for(int i=0;i<n;i++){//下面是释放堆和赋值
        free(ans[i]);
        ans[i]=NULL;
        free(coordinate[i]);
        coordinate[i]=NULL;
    }
    free(ans);
    ans=NULL;
    free(coordinate);
    coordinate=NULL;
    return 0;
}

int firstCheck(int *p1,int *p2){
    /*检测方法是，若两线段相交，则其中一个线段的最大横坐标必然大于另一线段的最小横坐标。
    纵坐标同理，共需进行四次检验*/
    if(max(p1[0],p1[2])<min(p2[0],p2[1]))
        return 0;
    if(max(p2[0],p2[1])<min(p1[0],p1[2]))
        return 0;
    if(max(p1[1],p1[3])<min(p2[1],p2[3]))
        return 0;
    if(max(p2[1],p2[3])<min(p1[1],p1[3]))
        return 0;
    return 1;
}

int specialCheck(int *p1,int *p2){
    //特殊情况是共线的情况
    int *p=(int *) malloc(4*sizeof (int));
    p[0]=p2[0]-p1[0];//得到
    p[1]=p2[1]-p1[1];//线段p2上一点与线段p1上一点组成的向量坐标表示
    p[2]=p1[2]-p1[0];//得到
    p[3]=p1[3]-p1[1];//线段p1的向量坐标表示
    if(crossProduct(p)==0){//两向量做叉乘
        p[0]=p2[2]-p1[0];
        p[1]=p2[3]-p1[1];//取p2上另一点与p1做叉乘
        if(crossProduct(p)==0){//共需两次判断，来判断p2是否与p1共线
            int check=0;      //要求两次叉乘结果均为0，则两线段共线
            int j1= findStart(p1);
            int j2= findEnd(p1);
            int j= findStart(p2);
            if((p2[j]<=p1[j2])&&(p2[j]>=p1[j1])){//先判断p2起点横坐标是否在线段p1范围内
                if((p2[j]==p1[j2])&&(p2[j]==p1[j1])){//判断两线段与y轴平行的情况
                    if((p2[j+1]<=p1[j2+1])&&(p2[j+1]>=p1[j1+1]))//此时判断p2起点纵坐标是否在线段p1范围内
                        check=1;//此时p2起点纵坐标在线段p1范围内，与y轴平行，满足条件
                }
                else check=1;//此时p2起点横坐标是在线段p1范围内，且不与y轴平行，满足条件
            }
            if(check==1){
                free(p);
                p=NULL;
                return 1;
            }//接下来将p1,p2颠倒，重复上面算法
            j1= findStart(p2);
            j2= findEnd(p2);
            j= findStart(p1);
            if((p1[j]<=p2[j2])&&(p1[j]>=p2[j1])){
                if((p1[j]==p2[j2])&&(p1[j]==p2[j1])){
                    if((p1[j+1]<=p2[j2+1])&&(p1[j+1]>=p2[j1+1]))
                        check=1;
                }
                else check=1;
            }
            if(check==1){
                free(p);
                p=NULL;
                return 1;
            }
            else{//共线但不满足上述条件，则不符合题意
                free(p);
                p=NULL;
                return -1;
            }
        }
    }
    free(p);
    p=NULL;
    return 0;//此时不共线
}

int generalCheck(int *p1,int *p2){
    int *p=(int *) malloc(4*sizeof (int));
    int *pp=(int *) malloc(4*sizeof (int));
    int check1=0,check2=0;//需要两次判断，来判断其中两线段各有至少一个端点使得另一个线段的两端点在其两侧
    p[0]=p2[0]-p1[0];
    p[1]=p2[1]-p1[1];
    p[2]=p1[2]-p1[0];//p和pp,[2][3]是为获取p1线段向量坐标表示
    p[3]=p1[3]-p1[1];//此时是取p1上一端点与p2上两端点分别组成两个向量
    pp[0]=p2[2]-p1[0];
    pp[1]=p2[3]-p1[1];
    pp[2]=p1[2]-p1[0];
    pp[3]=p1[3]-p1[1];
    if(crossProduct(p)!= crossProduct(pp))
        check1=1;
    if(check1==0){//一次检测不行则直接结束函数
        free(pp);
        pp=NULL;
        free(p);
        p=NULL;
        return 0;
    }//下面取p1上两端点与p2一端点组成向量，并与p2形成的向量做叉乘
    p[0]=p1[0]-p2[0];
    p[1]=p1[1]-p2[1];
    p[2]=p2[2]-p2[0];
    p[3]=p2[3]-p2[1];
    pp[0]=p1[2]-p2[0];
    pp[1]=p1[3]-p2[1];
    pp[2]=p2[2]-p2[0];
    pp[3]=p2[3]-p2[1];
    if(crossProduct(p)!= crossProduct(pp))
        check2=1;
    if(check2==1){
        free(pp);
        pp=NULL;
        free(p);
        p=NULL;
        return 1;
    }
    free(pp);
    pp=NULL;
    free(p);
    p=NULL;
    return 0;
}

int crossProduct(int *p){
    int ans=0;
    ans=p[0]*p[3]-p[1]*p[2];
    if(ans>0)
        return 1;
    else if(ans<0)
        return -1;
    else return 0;
}

int findStart(int *p){
    if(p[0]<p[2])
        return 0;
    if(p[0]>p[2])
        return 2;
    if(p[0]==p[2]){
        if(p[1]<p[3])
            return 0;
        else return 2;
    }
    return 0;
}

int findEnd(int *p){
    if(p[0]<p[2])
        return 2;
    if(p[0]>p[2])
        return 0;
    if(p[0]==p[2]){
        if(p[1]<p[3])
            return 2;
        else return 0;
    }
    return 0;
}

思路:

向量叉乘公式：
$$\begin{gathered} v_1(x_1,y_1,z_1)\times v_2(x_2,y_2,z_2)=(y_1{z}_2-y_2{z}_1,x_2{z}_1-z_2{x}_1,x_1{y}_2-x_2{y}_1) \\ 若是z_1=z_2=0 \\ 则结果为(0,0,x_1{y}_2-x_2{y}_1) \\ 引入向量叉乘是因为向量叉乘带有方向。 \\ 判断方向有点像高中学的右手定则，让v_1穿过掌心，四指指向v_2，此时大拇指所指的方向就是所得叉乘方向。 \\ 若是有两个点分别在线段两侧，则取线段上一个端点分别与另外两个点以及另一个端点形成三个向量， \\ 那么与那两个点形成的向量和其与端点形成的向量做叉乘所形成的两个新向量，方向相反 \\ 而当这两个线段，每个线段都可以找到至少一个端点，使得其做如上所述的叉乘形成方向不同（注意）的两个新向量 \\ 那么这两个线段必然相交。而为何需要都找到至少一个呢？ \end{gathered}$$
首先回答为什么只有一个线段找得到不行：

此时形成三个向量，显然可以在下面那条短的线段上找到两个端点满足上面所说的条件，但两线段不相交，因为另外一条长线段无法找到满足上面条件的端点。

那为什么是是方向不同而不是相反呢？

此时会发现两条线段在一个端点重合了，此时可以选择不重合的那个端点组成上述三条向量，其中两条重合，重合的两向量叉乘计算结果为0，但另外一个计算结果不为零。而重合那点可以组成一个(0,0)的向量，依然会发现，一个结果为0，另一个结果不为0。

而两个线段均找到这样的端点则可保证两条线段相交，而两条直线若是相交则必然每个线段的各个端点都满足。（不考虑共线情况）

初始检测：在开始一般性的检测之前，可以先进行关于必要性检测的初筛。可以发现，若是两线段若是有相交部分，那么就横坐标而言，一条线段的最小横坐标必然小于或等于另一线段的最大横坐标，纵坐标同理。而因此可对这两条线段的端点进行四次检测。若是检测不通过，那么可以直接进行下一条线段的比较。

特殊情况检测：我们上面没有考虑到两条直线共线的情况。在这种情况下，做上述两次叉乘结果均为0。为了可以进行检测，可以对线段两端点分为起点和终点：x坐标小的为起点，x相同则y坐标小的为起点。则若是两线段有重合部分，那么要么是线段一的起点在线段二上，要么是线段二的起点在线段一上，两种情况满足一个则可说明两线段有重合部分。这次检测分为三种情况 ：一是共线且有重合部分，则符合条件。二是共线但无重合部分，不符合条件，进行下一条线段检测。三是不共线，则进行一般情况的检测。

一般情况检测：经过上面两个检测，能确定此时线段不共线。则延续上面的思路，取线段上任意端点作向量起点，形成三个向量，并以线段本身的向量与另外两个向量分别做叉乘，判断是否方向不同。这个判断需要每个线段各做一次，共两次。若是第一次检测不通过则可直接结束函数。

经过三重检测，便可确定哪两条线段相交了。

注意：叉乘方向不同，体现在我上面所提到的向量坐标做叉乘的公式最后计算结果的情况不同，即是正、负和零（方向不同这句话并不严谨）。

072 【专业融合：动能】热能计算

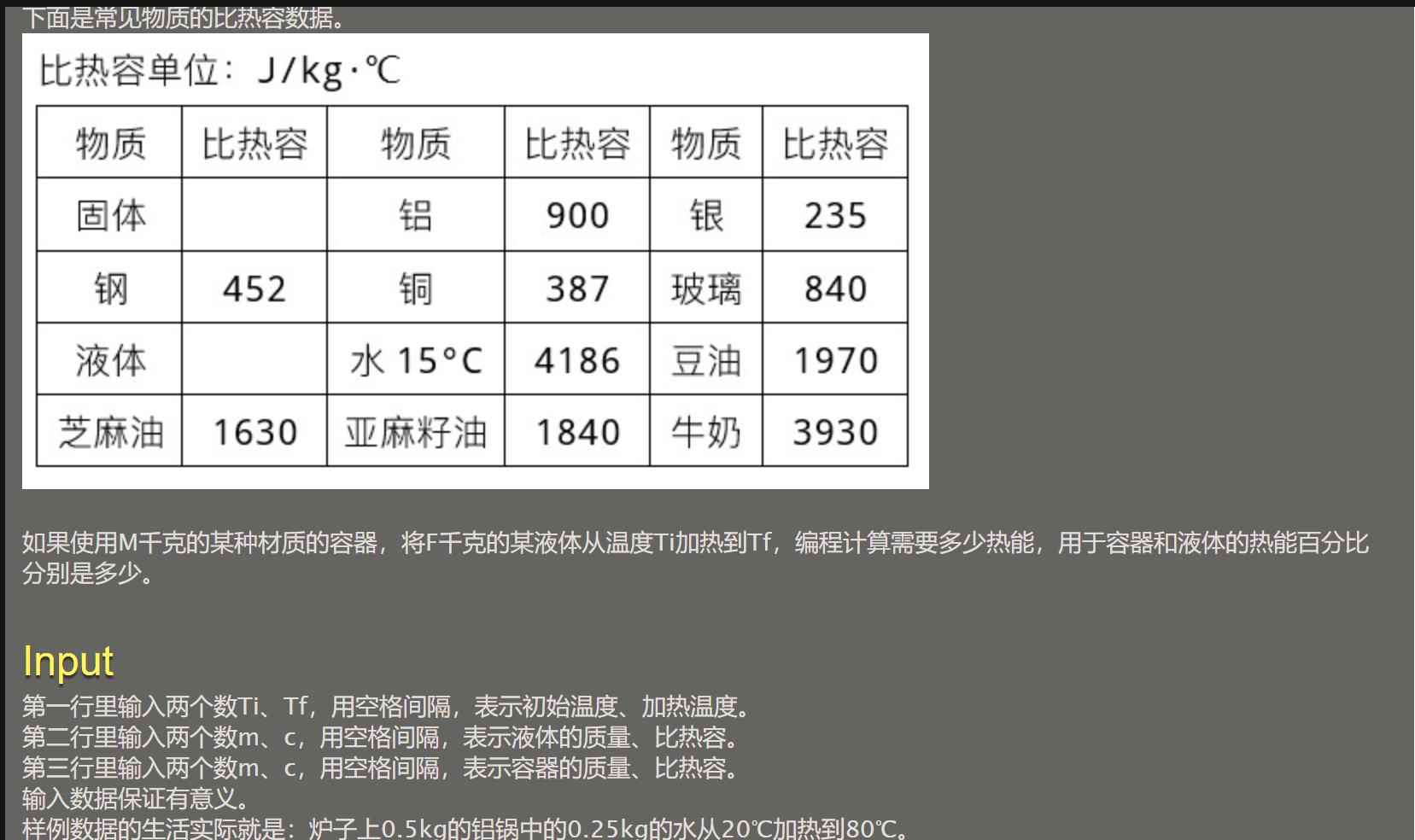
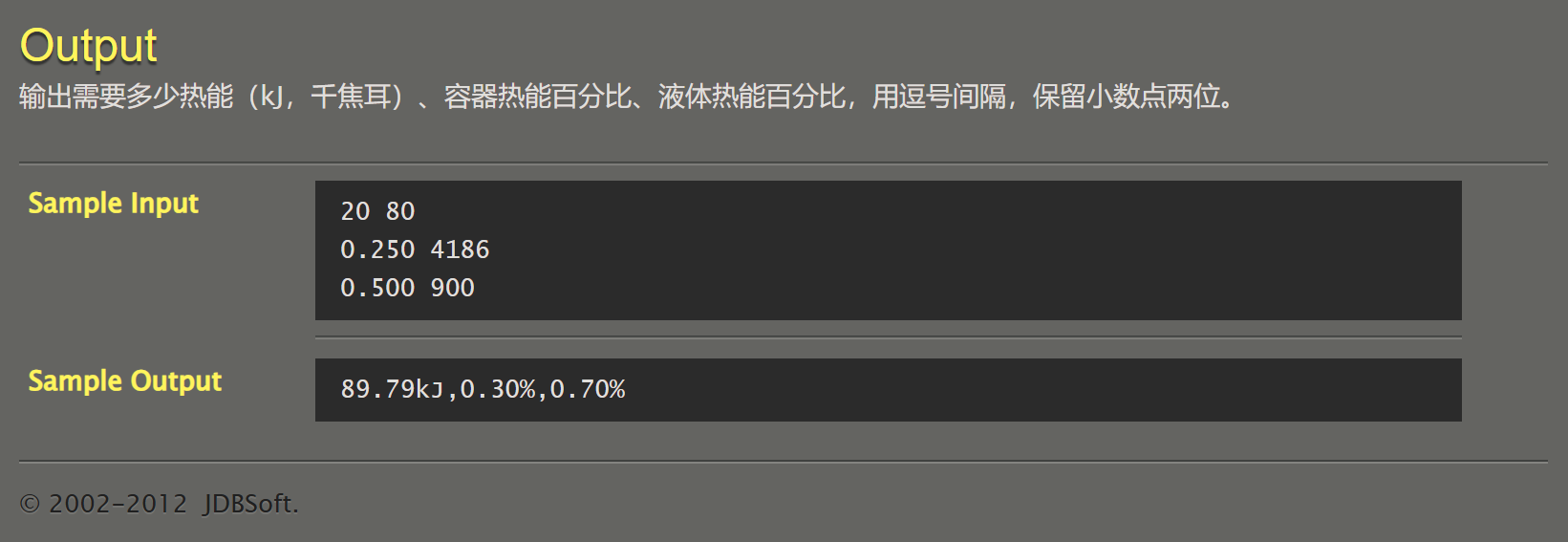
#include <stdio.h>

int main(void) {
    double ti,tf,m1,c1,m2,c2;
    //ti为初始温度，tf为加热后温度,m1、m2分别为液体和容器质量，c1、c2为热能百分比
    scanf(" %lf%lf%lf%lf%lf%lf",&ti,&tf,&m1,&c1,&m2,&c2);
    double q1=c1*m1*(tf-+ti),q2=c2*m2*(tf-ti);
    //q1、q2分别为液体和容器所需要的热量
    printf("%.2lfkJ,%.2lf%%,%.2lf%%\n",(q1+q2)/1000.0,(q2/(q1+q2)),(q1/(q1+q2)));
    return 0;
}

​ AC需要注意的是kJ，k小写，J大写。还有输出顺序，先容器，后液体。虽然是液体先被输入（笑）。

​ 题目错误：热能百分比样例输出错误，即是检测程序出错。加上了%却没有✖️100。但若是加上这步操作，则为WA。

073 成绩单

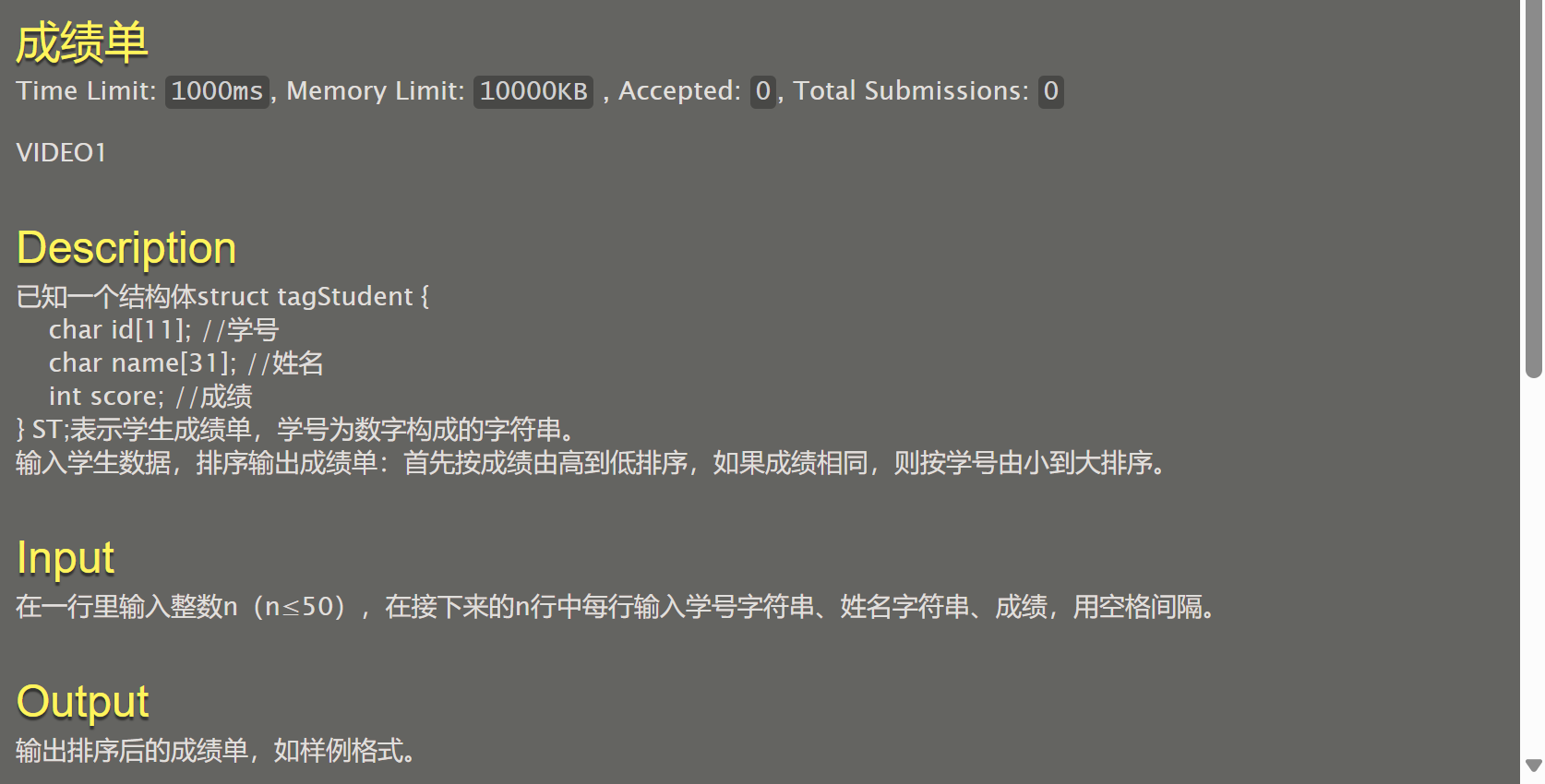
#include <stdio.h>
#include "stdlib.h"
#include "string.h"

struct tagStudent{//定义一个结构体，照着题目做就行
    char id[11];
    char name[31];
    int score;
};

void sequence(struct tagStudent **ppST,int n);//排序函数，对成绩进行排序

int main(void) {
    int n;
    scanf(" %d",&n);
    struct tagStudent **ppST=(struct tagStudent**)malloc(n*sizeof(struct tagStudent*));
    //定义结构体双指针
    for(int i=0;i<n;i++){ //共n次循环，写入数据,同时分配堆
        ppST[i]=(struct tagStudent*) malloc(sizeof(struct tagStudent));
        scanf(" %s %s %d",ppST[i]->id,ppST[i]->name,&ppST[i]->score);
    }
    sequence(ppST,n); //对其排序
    for(int i=0;i<n;i++){//依次打印到屏幕
        printf("%s %s %d\n",ppST[i]->id,ppST[i]->name,ppST[i]->score);
    }
    for(int i=0;i<n;i++){
        free(ppST[i]);//依次释放堆
        ppST[i]=NULL;//赋初值
    }
    free(ppST);
    ppST=NULL;
    return 0;
}

void sequence(struct tagStudent **ppST,int n){
    struct tagStudent *temps;
    int logEqual;//用来记录有几个数相等
    int len= strlen(ppST[0]->id);//获取学号位数，后面比较学号会用到
    for(int i=0;i<(n-1);i++){//依次比较分数，若后面大于前面，则交换
        for(int j=i+1;j<n;j++){
            if(ppST[i]->score<ppST[j]->score){//比较分数
                temps=ppST[i];
                ppST[i]=ppST[j];
                ppST[j]=temps;
            }
        }
    }
    //已按照分数实现排序
    for(int i=0;i<(n-1);i++){//依次比较前后分数是否相等
        logEqual=1;
        if(ppST[i]->score!=ppST[i+1]->score)//如果不相等直接进行下一次比较
            continue;
        for(int j=i+1;j<(n-1);j++){//相等则继续判断之后是否依然相等
            if(ppST[j]->score==ppST[j+1]->score)
                logEqual++;//计数有几个相等的分数
            else break;//不相等则停止计数
        }
        int cy=i;//复制此时i的值
        for(;i<(cy+logEqual);i++){//如上面算法相似，比较学号，后面比前面小则交换
            for(int j=(i+1);j<(cy+logEqual+1);j++){
                for(int m=0;m<len;m++){//比较第(i+1)个和第(j+1)的学号的大小,从大位到小位比较
                    if(ppST[i]->id[m]>ppST[j]->id[m]){//字符会转化为ASCII码序号进行比较
                        temps=ppST[i];
                        ppST[i]=ppST[j];
                        ppST[j]=temps;
                        break;//比较出一位即可不再比较
                    }
                    else if(ppST[i]->id[m]<ppST[j]->id[m])
                        break;//比较出一位即可不再比较
                }
            }
        }
    }
    temps=NULL;//因为没有给temps分配堆，故不需要释放堆，若释放则会出现乱码
}

思路：先排成绩，再在成绩相同的结构体中排学号。其中定义结构体双指针，使得可以在之间进行地址的交换，从而实现交换数据。

注意：

1.在交换地址时所使用的中间指针，由于没有分配堆，不需要进行内存释放。

2.在进行比较的时候，不要忽略使用break。若是忽视其中一个break就会导致结果出错，因为会出现过多比较的情况。比如：学号之间比较时，只要有一位不同就可以停止比较了，否则会进行下面位次的比较，导致出错。

字符串比较大小：这题需要学号之间进行比较，而字符串之间比较大小可以采用每个字符依次比较。字符在比较的时候会转化为ASCII码序号进行比较。比如字符‘0’会转化为数字48，‘1’转化为49。因此可以比较。此外：可以不按照题目提示，将学号的类型定义为long long，应该也能行得通。

074 【专业融合：数学】中位数

#include <stdio.h>
#include "stdlib.h"

void beOrderly(int *ppDate);//对获得数据进行排序,n表示共有几行，排除包含负数的行
int getItem(int *ppInput);//获取数字有几位

int main() {
    int **ppInput=(int**) malloc(100*sizeof (int*)),i=0;
    //**ppInput用来接受输入数据,i用来记录有(i+1)行
    int *nnew=(int *) malloc(100*sizeof (int));
    //*new用来存放新序列，存放前面几行连在一起，但是去除了0的新序列。
    while(1){
        ppInput[i]=(int*) malloc(sizeof (int));
        ppInput[i][0]=0;
        int j=0;
        while(1){
            ppInput[i]=(int*) realloc(ppInput[i],(j+1)*sizeof (int));
            scanf(" %d",&ppInput[i][j]);
            if(ppInput[i][j]==0)//输入数据为0时，结束该次小循环
                break;
            if(ppInput[i][j]<0)
                goto break_;//如果输入数据小于1，直接跳出大循环
            j++;
        }
        i++;
    }
    break_:;
    for(int j=1;j<=i;j++){
        for(int m=0;m<j;m++){
            int n=0;
            while(1){
                if(ppInput[m][n]==0){//每次遇到0都停下来
                    //printf("1");
                    if(m==(j-1)){//当m刚好到当前目标行数时
                        int num=0;//用来统计此时共有多少数字
                        for(int k=0;k<=m;k++)
                            num+= getItem(ppInput[k]);//依次加上每行的数字个数
                        int cy=num;//储存共有多少数字
                        num=0;
                        for(int k=0;k<=m;k++){
                            if(k>0)//当此时对于1行时，统计之前行数字个数（除了0）
                                num+=getItem(ppInput[k-1]);
                            for(int l=0;l< getItem(ppInput[k]);l++){
                                if((k==m)&&(l== getItem(ppInput[k])-1)){
                                    //最后一个数字需要特殊处理，要在其之后加上0，以此保证获取个数函数
                                    //的正常运行
                                    nnew[(num + l)]=ppInput[k][l];
                                    nnew[num + l + 1]=0;
                                }
                                else
                                    nnew[(num + l)]=ppInput[k][l];//获取新数列
                            }
                        }
                        beOrderly(nnew);//对新数列进行排序
                        if(cy%2==1){//如果为奇数个
                            double ans=nnew[cy / 2];
                            printf("%.6lf\n",ans);
                        }
                        else{//偶数个情况
                            double ans1=nnew[cy / 2 - 1];
                            double ans2=nnew[cy / 2];
                            double ans=(ans1+ans2)/2;
                            printf("%.6lf\n",ans);
                        }
                        break;
                    }
                    else//若是0，但不是此时要求的最后一个0，直接结束此次循环，使得这个0不被打印出来
                        break;
                }//当不是0时，将输入的数依次输出
                printf("%d ",ppInput[m][n]);
                n++;
            }
        }
    }
    //释放内存和赋值操作
    free(nnew);
    nnew=NULL;
    for(int j=0;j<i;j++){
        free(ppInput[j]);
        ppInput[j]=NULL;
    }
    free(ppInput);
    ppInput=NULL;
    return 0;
}

void beOrderly(int *ppDate){
    int num= getItem(ppDate);//获取有几位
    for(int j=0;j<num-1;j++){//经典排序方法，后面小于前面则交换位置
        for(int m=j+1;m<num;m++){
            if(ppDate[j]>ppDate[m]){
                int temps=ppDate[j];
                ppDate[j]=ppDate[m];
                ppDate[m]=temps;
            }
        }
    }
}

int getItem(int *ppInput){
    int num=0;
    while(1){
        if(ppInput[num]==0){
            return num;//获取数字个数，除了0
        }
        num++;
    }
}

思路：先利用双重指针依次获取每行数据，然后在打印过程中，将打印行数依次从1到n行（不包括存在负数的行），当打印到第n行时，不要打印第n行之前的0。因此需要检测每个需要打印的数是否为0。若为0且不处于第n行，那么结束这行的打印；若是处于第n行，则需要开始求中位数。求中位数，设置一个新指针用来获取一个数列，这个数列包括n行及n行之前所有数据（不包括0），然后对这个数列里数据进行排序并获取数列中共有多少位数字，分为奇数个和偶数个两种情况分别求出中位数。

注意：使用realloc()函数容易造成内存泄露，慎用（可在定义指针时分配足够大的堆）。内存泄露容易造成RE。

075 【专业融合：力学】火箭发射模拟

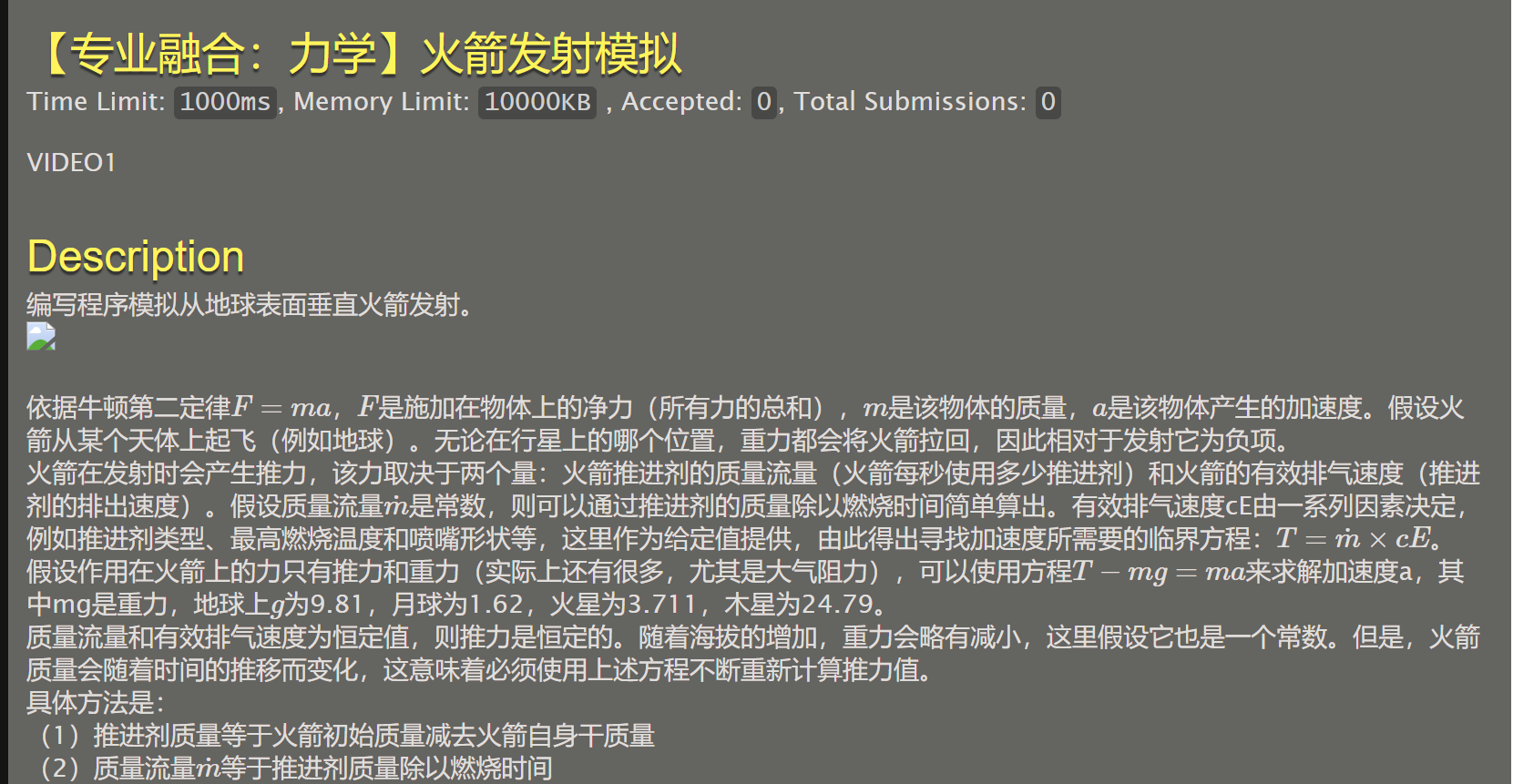
#include <stdio.h>

double calculate(double T,double m,double g,double velocity, \
                 double mass_flow,double altitude,double burn_time);
//用于计算的函数，其中T,g,mass_flow为定值
int main(void) {
    int start_mass,rocket_mass,burn_time,exhaust_velocity;
    //分别为起始质量，火箭本身质量，燃烧时间，有效排气速度
    double gravity_acceleration;//重力加速度
    scanf(" %d %d %d %d %lf",&start_mass,&rocket_mass,&burn_time, \
            &exhaust_velocity,&gravity_acceleration);
    double mass_flow=(double )(start_mass-rocket_mass)/(double )burn_time;
    //计算质量流量
    double force=mass_flow*exhaust_velocity;//计算推力
    double ans= calculate(force,start_mass,gravity_acceleration,\
                          0,mass_flow,0,burn_time);
    printf("%.3lfkm",ans/1000);
    return 0;
}

double calculate(double T,double m,double g,double velocity,\
                 double mass_flow,double altitude,double burn_time){
    if(burn_time<=0){//燃烧时间耗尽时，返回海拔高度
        return altitude;
    }
    double a=T/m;//这里正确应该是a=T/m-g，但与样例不符，可以推测为样例输出再次错误
    double time_step=0.1;
    velocity+=a*time_step;//每次加速
    altitude+=velocity*time_step;//高度增加
    burn_time-=0.1;
    m-=mass_flow*time_step;//总质量减少
    return calculate(T,m,g,velocity,mass_flow,altitude,burn_time);//用新数据再次计算
}

题目检测样例错误：要是按照题目所说令a=T/m-g，那么输出结果和样例不同，只有令a=T/m，才能得到相同的结果。

思路：设置一个循环函数，给其必要初始值，然后每次让其中特定参数发生变化，直到燃烧时间小于或等于0，返回 高度，因为这是浮点数和整数比较大小。

076 【专业融合：航天】卫星定位

#include <stdio.h>
#include <math.h>

#define c 299792.458
#define N 11

double X[N],A[N],B[N],C[N],T[N];

void print1(double A[N],int n) { //输出
    int i,tmps;
    double a;
    for (i=0; i<n-1; i++){
        tmps=(int)(A[i]*10000);
        a=(double)tmps/10000.0;
        printf("%.4lf,",a);
    }
    tmps=(int)(A[n-1]*10000);
    a=(double)tmps/10000.0;
    printf("%.4lf",a);
}

// 计算代数余子式函数，结果=dest
int GetCoFactor(double dest[N][N], double src[N][N], int row, int col, int n)
{
	int i, j;
	int colCount=0,rowCount=0;
	for(i=0; i<n; i++ ) {
		if( i!=row ) {
			colCount = 0;
            for(j=0; j<n; j++ )
				if( j != col ) { //当j不是元素时
					dest[rowCount][colCount] = src[i][j];
					colCount++;
				}
			rowCount++;
		}
	}
	return 1;
}

// 递归计算行列式，结果=返回值
double CalcDeterminant(double mat[N][N], int n)
{
	int i,j;
	double det = 0; //行列式值
	double minor[N][N]; // allocate 余子式矩阵

    // n 必须 >= 0，当矩阵是单个元素时停止递归
	if( n == 1 ) return mat[0][0];
	for(i = 0; i < n; i++ ) {
		GetCoFactor(minor, mat, 0, i , n);
		det += ( i%2==1 ? -1.0 : 1.0 ) * mat[0][i] * CalcDeterminant(minor,n-1);
	}
	return det;
}
// 伴随矩阵法矩阵求逆 , 结果存放到 inv 数组
void MatrixInversion(double J[N][N], int n)
{
	int i,j;
    double det, temp [N][N], minor[N][N];
    double inv[N][N];

	det = 1.0/CalcDeterminant(J,n); //计算行列式
	for(j=0; j<n; j++)
		for(i=0; i<n; i++) {
			// 得到矩阵A(j,i)的代数余子式
			GetCoFactor(minor,J,j,i,n);
			inv[i][j] = det*CalcDeterminant(minor,n-1);
			if( (i+j)%2 == 1)
				inv[i][j] = -inv[i][j];
		}
	//结果存回J矩阵
	for(j=0; j<n; j++)
		for(i=0; i<n; i++)
			J[i][j] = inv[i][j];
}

// 由Xn计算函数Fn，结果存放到 F
void CalcF(double F[N],double X[N],int n) {
    double f;
    int i;
    for (i=0; i<n; i++) {
        switch (i+1) {
            case 1:
                f=(X[0]-A[0])*(X[0]-A[0])+(X[1]-B[0])*(X[1]-B[0])+(X[2]-C[0])*(X[2]-C[0])-(c*(T[0]-X[3]))*(c*(T[0]-X[3]));
                break;
            case 2:
                f=(X[0]-A[1])*(X[0]-A[1])+(X[1]-B[1])*(X[1]-B[1])+(X[2]-C[1])*(X[2]-C[1])-(c*(T[1]-X[3]))*(c*(T[1]-X[3]));
                break;
            case 3:
                f=(X[0]-A[2])*(X[0]-A[2])+(X[1]-B[2])*(X[1]-B[2])+(X[2]-C[2])*(X[2]-C[2])-(c*(T[2]-X[3]))*(c*(T[2]-X[3]));
                break;
            case 4:
                f=(X[0]-A[3])*(X[0]-A[3])+(X[1]-B[3])*(X[1]-B[3])+(X[2]-C[3])*(X[2]-C[3])-(c*(T[3]-X[3]))*(c*(T[3]-X[3]));
        }
        F[i]=f;
    }
}

// 由Xn计算偏导数Jacobian矩阵F'n，结果存放到 J
void CalcJ(double J[N][N],double X[N],int n) {

    double f;
    int i,j;
    for (i=0; i<n; i++)
        switch (i+1) {
            case 1:
                for (j=0; j<n; j++) {
                    switch (j+1) {
                        case 1: f=2*(X[0]-A[0]);break;
                        case 2: f=2*(X[1]-B[0]);break;
                        case 3: f=2*(X[2]-C[0]);break;
                        case 4: f=2*c*c*(T[0]-X[3]);break;
                    }
                    J[i][j]=f;
                }
                break;
            case 2:
                for (j=0; j<n; j++) {
                    switch (j+1) {
                        case 1: f=2*(X[0]-A[1]);break;
                        case 2: f=2*(X[1]-B[1]);break;
                        case 3: f=2*(X[2]-C[1]);break;
                        case 4: f=2*c*c*(T[1]-X[3]);break;
                    }
                    J[i][j]=f;
                }
                break;
            case 3:
                for (j=0; j<n; j++) {
                    switch (j+1) {
                        case 1: f=2*(X[0]-A[2]);break;
                        case 2: f=2*(X[1]-B[2]);break;
                        case 3: f=2*(X[2]-C[2]);break;
                        case 4: f=2*c*c*(T[2]-X[3]);break;
                    }
                    J[i][j]=f;
                }
                break;
            case 4:
                for (j=0; j<n; j++) {
                    switch (j+1) {
                        case 1: f=2*(X[0]-A[3]);break;
                        case 2: f=2*(X[1]-B[3]);break;
                        case 3: f=2*(X[2]-C[3]);break;
                        case 4: f=2*c*c*(T[3]-X[3]);break;
                    }
                    J[i][j]=f;
                }
                break;
        }
}

// 计算 J^-1* F，结果存放到 R
void CalcJF(double R[N], double J[N][N], double F[N], int n) {
	int i,j,k;
	for (i=0; i<n; i++) {
		R[i]=0.0;
		for (j=0; j<n; j++)
			R[i] = R[i] + J[i][j]*F[j];
	}
}

// 计算 X=X0-R，结果存放到 X
void CalcX(double X[N],double X0[N],double R[N],int n) {
	int i;
	for (i=0; i<n; i++)
		X[i]=X0[i]-R[i];
}

// 计算 A=B，结果存放到 A
void AequB(double A[N],double B[N],int n) {
	int i;
	for (i=0; i<n; i++)
		A[i]=B[i];
}

// 计算 F-
double Ferror(double F[N], int n) {
	double m=0;
	int i;
	for (i=0; i<n; i++) {
		double t=fabs(F[i]);
		if (m<t) m = t;
	}
	return m;
}

// Newton–Raphson method 牛顿迭代法求非线性方程组的根，存放到X0
void mvNewtons(double X0[N], int n, double e) {
	// Guess为初始猜测值 e为迭代精度要求
	int k;
	double J[N][N],Y[N][N];
	double X[N],R[N],F[N];
	//X0一开始为初始猜测值
	for (k=1; k<=20; k++) { //限定20次迭代
		CalcF(F,X0,n); //计算F矩阵
		CalcJ(J,X0,n); //计算Jacobian矩阵F'n(x0)
		MatrixInversion(J, n); // 求J的逆矩阵 J^-1
		CalcJF(R,J,F,n); // R=J^-1 * F
		CalcX(X,X0,R,n); // X=X0-R
		AequB(X0,X,n); // X0=X 下次迭代
		if (Ferror(F,n)<e) break; //达到精度要求，终止迭代
	}
}

void scanf1(double A[N],int n){
    for(int i=0;i<n;i++) {
        scanf(" %lf",&A[i]);
    }
}

int main() {
	int n=4;
	for(int i=0;i<4;i++){
		scanf(" %lf %lf %lf",&A[i],&B[i],&C[i]);
	}
    scanf1(T,n);
    scanf1(X,n);
	mvNewtons(X,n,1e-6); //根存放在X
	print1(X,3);
	return 0;
}

这题不做解释，不做解析。太逆天了，这还是c语言实验吗…

077 【专业融合：航海】水下声学定位

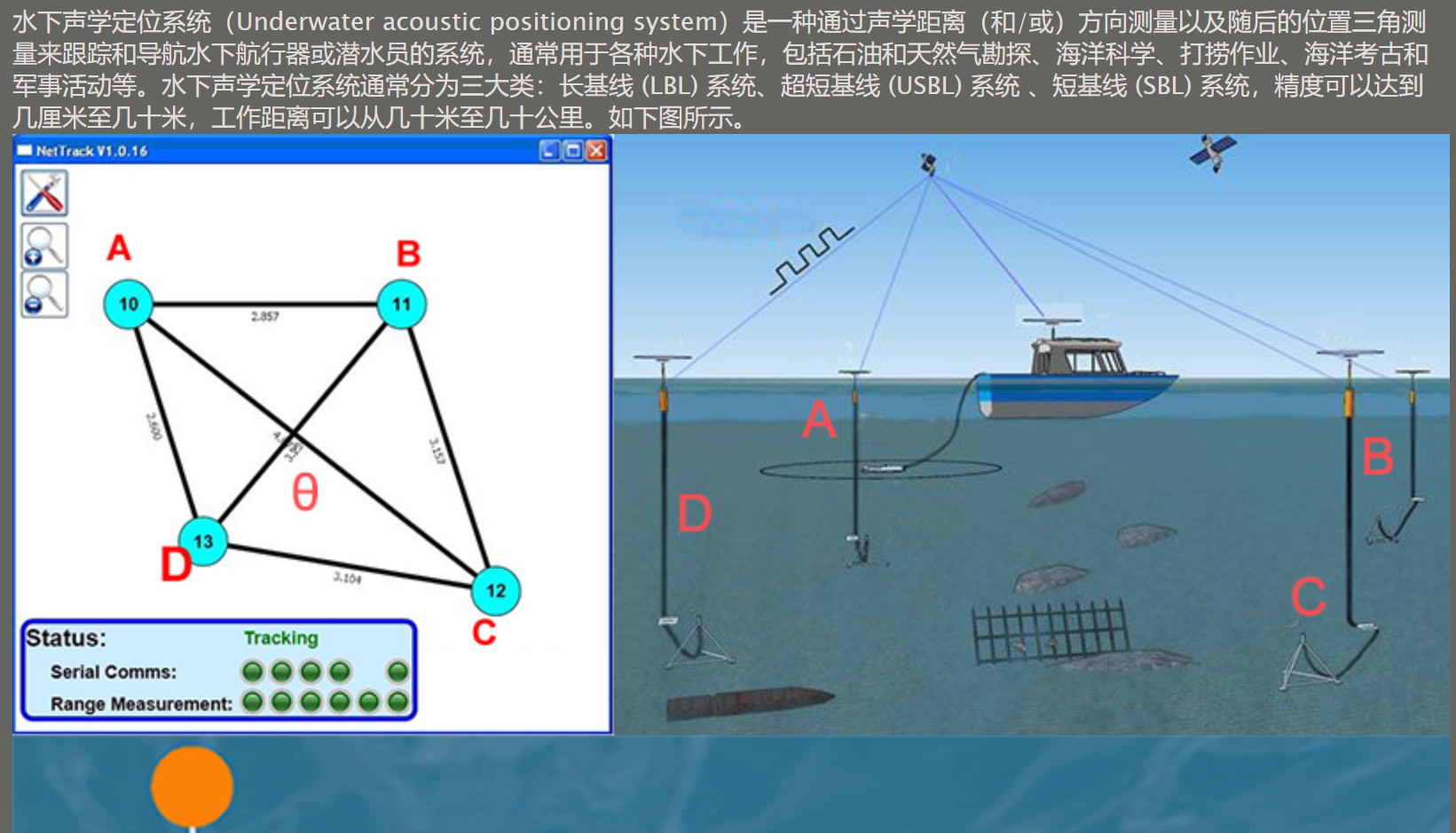
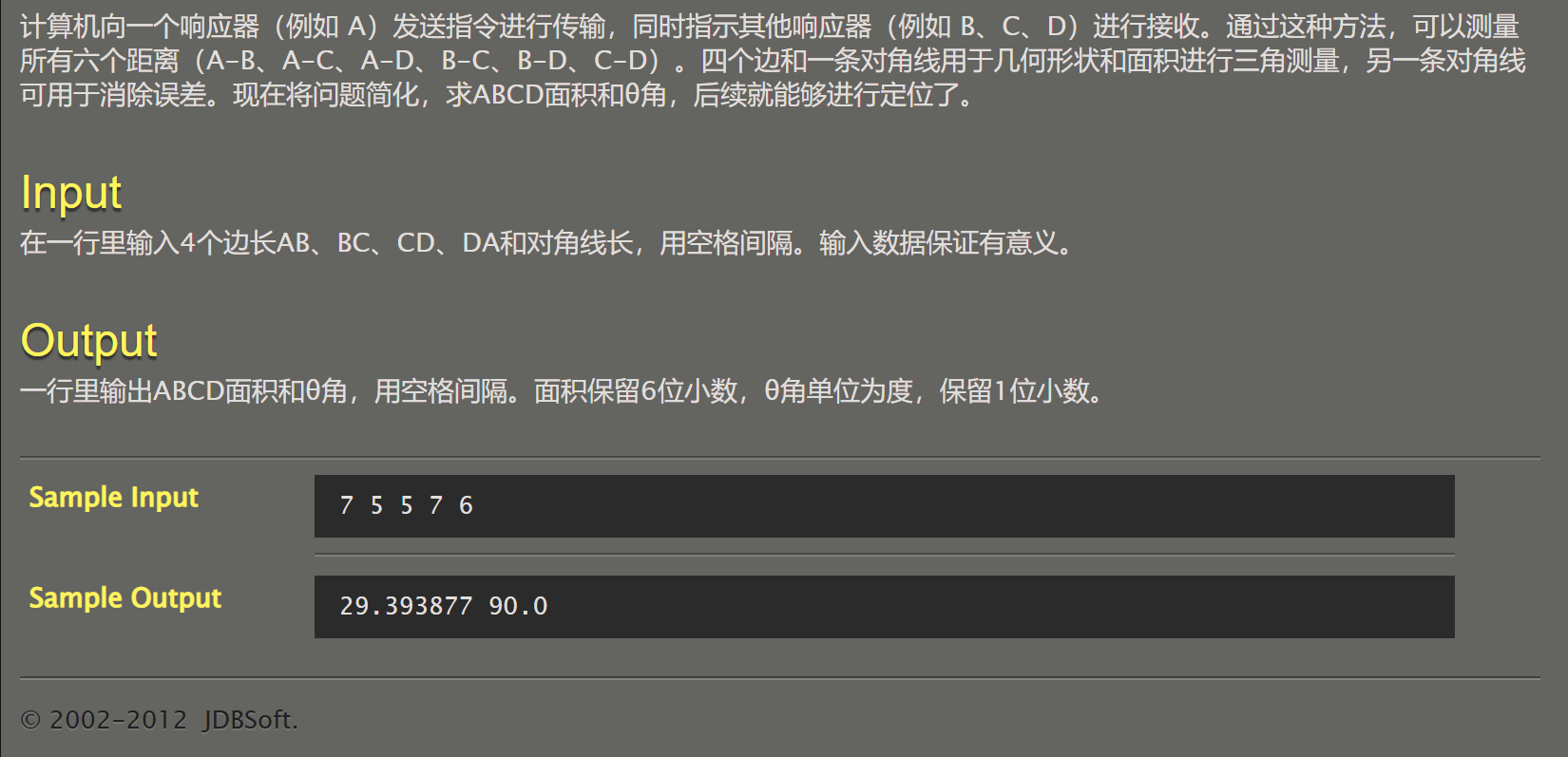
#include "stdio.h"
#include "math.h"
#define PI 3.14159265356
int main(){
    double AB,BC,CD,DA,AC;
    scanf(" %lf %lf %lf %lf %lf",&AB,&BC,&CD,&DA,&AC);
    double p1=(AB+BC+AC)/2.0;
    double p2=(CD+DA+AC)/2.0;//计算三角形半周长用于海伦公式计算
    double area=sqrt(p1*(p1-AB)*(p1-BC)*(p1-AC))+sqrt(p2*(p2-CD)*(p2-DA)*(p2-AC));
    //海伦公式计算面积
    double tan_delta=(4*area)/(BC*BC+DA*DA-AB*AB-CD*CD);//公式计算夹角正切
    double delta= atan(tan_delta)*180/PI;//反正切，并转换为角度制
    printf("%.6lf %.1lf",area,delta);
    return 0;
}

题目不明确之处：1.输入的对角线长度为AC的长度。2.所求角度为DC边对应的对角线的夹角。

思路：

1.面积：将四边形依照对角线划分为两个三角形，然后利用海伦公式求解。

$$\begin{gathered} 海伦公式: \\ p=\frac{a+b+c}{2}(a,b,c为三角形的三条边) \\ 三角形面积S=\sqrt{p(p-a)(p-b)(p-c)} \end{gathered}$$

2.角度：需要先分别证明两个公式

$$\begin{gathered} 1.A{D}^2+B{C}^2-A{B}^2-C{D}^2=2AC\times BD\times \cos \theta \\ 2.S=\frac{1}{2}\times AC\times BD\times \sin \theta \end{gathered}$$

以此图为例。对角线交点为O。
$$\begin{gathered} 要证：A{D}^2+B{C}^2-A{B}^2-C{D}^2=2AC\cdot BD\cdot \cos \theta \\ 证明：首先有四个余弦定理 \\ A{D}^2=A{O}^2+D{O}^2-2\cdot AO\cdot DO\cdot \cos (\pi -\theta ) \\ A{B}^2=A{O}^2+B{O}^2-2\cdot AO\cdot BO\cdot \cos (\theta ) \\ B{C}^2=B{O}^2+C{O}^2-2\cdot BO\cdot CO\cdot \cos (\pi -\theta ) \\ C{D}^2=C{O}^2+D{O}^2-2\cdot CO\cdot DO\cdot \cos (\theta ) \\ 其中\cos (\pi -\theta )=-\cos \theta \\ 所以有A{B}^2+B{C}^2=A{O}^2+D{O}^2+B{O}^2+C{O}^2+2\cdot \cos \theta \cdot (AO\cdot BO+BO\cdot CO) \\ A{D}^2+C{D}^2=A{O}^2+D{O}^2+B{O}^2+C{O}^2-2\cdot \cos \theta \cdot (AO\cdot DO+CO\cdot DO) \\ 两式想减得到(A{B}^2+B{C}^2)-(A{D}^2+C{D}^2)=2\cdot \cos \theta \cdot (AO\cdot (BO+DO)+CO\cdot (BO+DO)) \\ 得到(A{B}^2+B{C}^2)-(A{D}^2+C{D}^2)=2\cdot \cos \theta \cdot (BD\cdot (AO+CO)) \\ 因此证明A{D}^2+B{C}^2-A{B}^2-C{D}^2=2AC\cdot BD\cdot \cos \theta \end{gathered}$$
然后证明第二个公式:
$$\begin{gathered} 要证：S=\frac{1}{2}\cdot AC\cdot BD\cdot \sin \theta \\ 证明：首先\sin \theta =\sin (\pi -\theta ) \\ 因此S=\frac{1}{2}\cdot \sin \theta \cdot (AO\cdot DO+AO\cdot BO+BO\cdot CO+CO\cdot DO) \\ 进行合并同类项，并整理得到S=\frac{1}{2}\cdot AC\cdot BD\cdot \sin \theta \end{gathered}$$
将两个公式合并在一起：
$$\begin{gathered} 将第一个公式中的AC\cdot BD用第二个公式变形替代即是AC\cdot BD=\frac{2\cdot S}{\sin \theta } \\ 替换后得到A{D}^2+B{C}^2-A{B}^2-C{D}^2=\frac{4\cdot S\cdot \cos \theta }{\sin \theta } \\ 因此有\tan \theta =\frac{4\cdot S}{A{D}^2+B{C}^2-A{B}^2-C{D}^2} \end{gathered}$$
因此可以通过这个公式计算该角的tan值，再利用反三角函数，即可求出具体角度。

079 【专业融合：材料】晶体结构

#include "stdio.h"
#include "stdlib.h"
#include "string.h"
#include "math.h"
#define NA  6.022e23
double mass(char *p);//获取原子质量
double radius(char *p);//获取原子半径
double num(char *p);//确认晶胞内有几个原子

int main(){
    int n;
    char **elements;
    scanf(" %d",&n);//记录有几个元素
    elements=(char**)malloc(n*sizeof(char*));
    for(int i=0;i<n;i++){
        elements[i]=(char*) malloc(2*sizeof (char));
        scanf(" %s",elements[i]);//依次记录每个元素
    }
    for(int i=0;i<n;i++){
        int nm= num(elements[i]);//获取此时晶胞中原子数目
        double r= radius(elements[i]);//获取原子半径
        double m=mass(elements[i]);//获取原子质量
        double a;
        if(nm==1){//由个数判断出晶胞类型，从而计算边长
            a=2.0*r*pow(10,-10);;
        }
        else if(nm==2){
            a=4*r/ sqrt(3)*pow(10,-10);;
        }
        else{
            a=2*r* sqrt(2)*pow(10,-10);
        }
        double volume=pow(a,3);//计算晶胞体积
        double density=(nm*m)/(volume*NA);//计算晶胞密度
        printf("%.2lf\n",density);
    }
    for(int i=0;i<n;i++){
        free(elements[i]);
        elements[i]=NULL;
    }
    free(elements);
    elements=NULL;
    return 0;
}

double mass(char *p){
    if(strcmp(p,"Po")==0){
        return 208.998;
    }
    if(strcmp(p,"Li")==0){
        return 6.941;
    }
    if(strcmp(p,"Na")==0){
        return 22.989770;
    }
    if(strcmp(p,"Cr")==0){
        return 51.9961;
    }
    if(strcmp(p,"Mn")==0){
        return 54.938049;
    }
    if(strcmp(p,"Fe")==0){
        return 55.845;
    }
    if(strcmp(p,"Mo")==0){
        return 95.94;
    }
    if(strcmp(p,"Ta")==0){
        return 180.9479;
    }
    if(strcmp(p,"Al")==0){
        return 26.981538;
    }
    if(strcmp(p,"Ca")==0){
        return 40.078;
    }
    if(strcmp(p,"Ni")==0){
        return 58.6934;
    }
    if(strcmp(p,"Cu")==0){
        return 63.546;
    }
    if(strcmp(p,"Ge")==0){
        return 72.64;
    }
    if(strcmp(p,"Ag")==0){
        return 107.8682;
    }
    if(strcmp(p,"Pt")==0){
        return 195.078;
    }
    if(strcmp(p,"Au")==0){
        return 196.96655;
    }
    if(strcmp(p,"Pb")==0){
        return 207.2;
    }
    return 0;
}
double radius(char *p){
    if(strcmp(p,"Po")==0){
        return 168.0;
    }
    if(strcmp(p,"Li")==0){
        return 152.0;
    }
    if(strcmp(p,"Na")==0){
        return 186.0;
    }
    if(strcmp(p,"Cr")==0){
        return 128.0;
    }
    if(strcmp(p,"Mn")==0){
        return 127.0;
    }
    if(strcmp(p,"Fe")==0){
        return 126.0;
    }
    if(strcmp(p,"Mo")==0){
        return 139.0;
    }
    if(strcmp(p,"Ta")==0){
        return 146.0;
    }
    if(strcmp(p,"Al")==0){
        return 143.0;
    }
    if(strcmp(p,"Ca")==0){
        return 197.0;
    }
    if(strcmp(p,"Ni")==0){
        return 124.0;
    }
    if(strcmp(p,"Cu")==0){
        return 128.0;
    }
    if(strcmp(p,"Ge")==0){
        return 122.0;
    }
    if(strcmp(p,"Ag")==0){
        return 144.0;
    }
    if(strcmp(p,"Pt")==0){
        return 139.0;
    }
    if(strcmp(p,"Au")==0){
        return 144.0;
    }
    if(strcmp(p,"Pb")==0){
        return 175.0;
    }
    return 0;
}
double num(char *p){
    if(strcmp(p,"Po")==0){
        return 1.0;
    }
    if(strcmp(p,"Li")==0){
        return 2.0;
    }
    if(strcmp(p,"Na")==0){
        return 2.0;
    }
    if(strcmp(p,"Cr")==0){
        return 2.0;
    }
    if(strcmp(p,"Mn")==0){
        return 2.0;
    }
    if(strcmp(p,"Fe")==0){
        return 2.0;
    }
    if(strcmp(p,"Mo")==0){
        return 2.0;
    }
    if(strcmp(p,"Ta")==0){
        return 2.0;
    }
    if(strcmp(p,"Al")==0){
        return 4.0;
    }
    if(strcmp(p,"Ca")==0){
        return 4.0;
    }
    if(strcmp(p,"Ni")==0){
        return 4.0;
    }
    if(strcmp(p,"Cu")==0){
        return 4.0;
    }
    if(strcmp(p,"Ge")==0){
        return 4.0;
    }
    if(strcmp(p,"Ag")==0){
        return 4.0;
    }
    if(strcmp(p,"Pt")==0){
        return 4.0;
    }
    if(strcmp(p,"Au")==0){
        return 4.0;
    }
    if(strcmp(p,"Pb")==0){
        return 4.0;
    }
    return 0;
}

注意：表中给的原子半径单位是pm，要通过乘以10的-10次方转化成cm单位。还有别输错数据了，以及对于元素周期表不要选择右边的打开周期表大图，而要选择左边的下载周期表，因为右边的没有Po元素的原子半径，左边的更加全面。

思路：由每个输入字符串，选择相应的原子质量，半径，以及晶胞中的原子个数，再由此选择晶胞边长计算方法。最后由公式计算得出答案。这题不难，就是输入数据很折磨人。

此外：我在这里用于比较字符串的函数是strcmp()函数，定义于<string.h>头文件中。表示string compare,若是相同，返回0，前一个字符串小于后一个返回-1，否则返回+1。

080 【专业融合：化学】原子计数

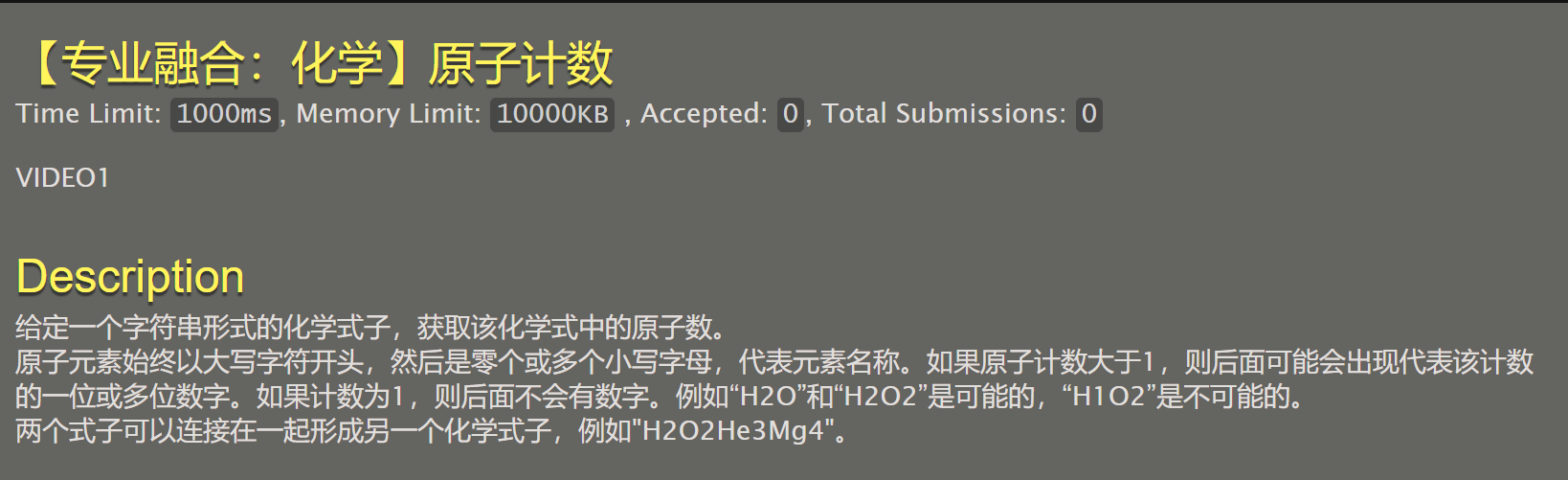
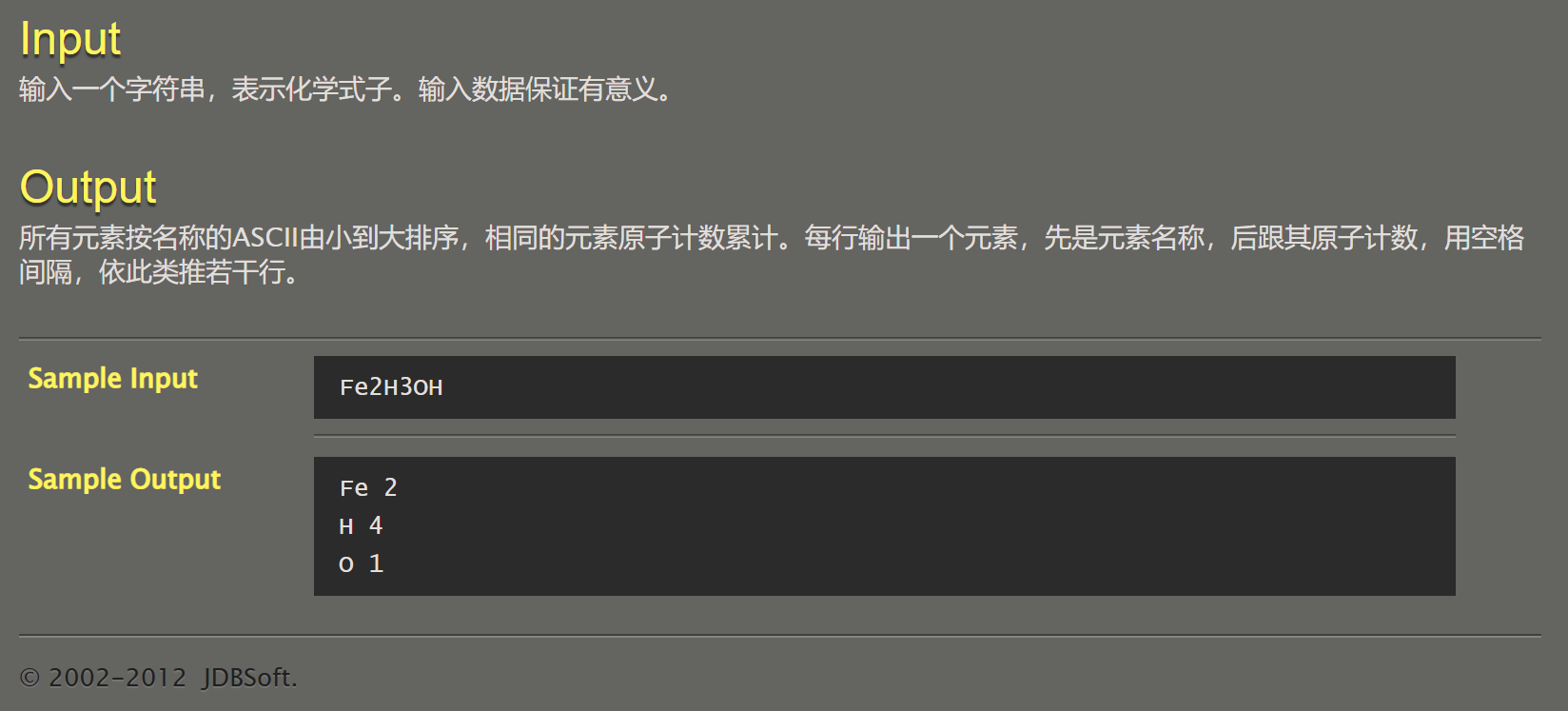
#include "stdio.h"
#include "stdlib.h"
#include "string.h"
#include "ctype.h"

int get_elements(char *chemical,char **elements,int *num);//获取元素排列
void get_orderly(char **elements,int *num,int elements_total_number);//对元素按ASCII码进行排序

int main(){
    char *chemical_formula=(char*) malloc(300*sizeof (char));//化学式字符串
    char **elements=(char**) malloc(300*sizeof (char*));//用于存储各个元素
    for(int i=0;i<300;i++){
        elements[i]=(char*) malloc((100*sizeof (char)));
    }
    int *number_elements=(int*) malloc(300*sizeof (int));//用于储存各个元素个数
    for(int i=0;i<300;i++)
        number_elements[i]=0;
    scanf(" %s",chemical_formula);//读取化学式
    int elements_total_number=get_elements(chemical_formula, elements, number_elements);
    //读取原子个数，接收元素的总数
    get_orderly(elements, number_elements, elements_total_number);//对元素排序
    for(int i=0; i < elements_total_number; i++){
        printf("%s %d\n",elements[i],number_elements[i]);//依次打印
    }
    for(int i=0;i<300;i++){
        free(elements[i]);
        elements[i]=NULL;
    }
    free(elements);
    elements=NULL;
    free(number_elements);
    number_elements=NULL;
    free(chemical_formula);
    chemical_formula=NULL;
    return 0;
}

int get_elements(char *chemical,char **elements,int *num){
    if(chemical==NULL||elements==NULL||num==NULL)
        exit(1);
    unsigned long long len= strlen(chemical);//获取化学式长度,strlen返回值类型为unsigned long long
    int n=0;//计数元素数量
    char element[100];//临时储存元素
    for(int i=0;i<len;i++){
        element[0]=chemical[i];
        int ctr=1;
        while (islower(chemical[i+1])){//若是小写则记录下来
            element[ctr]=chemical[i+1];
            i++;//向后移动一位
            ctr++;//写入element的字母增加一位
        }
        element[ctr]='\0';//给予字符串结束符号
        int number=0;
        if(!isdigit(chemical[i+1]))//如果元素后没有数字，则按一个算
            number=1;
        while(isdigit(chemical[i+1])){//有数字进入循环
            number=number*10+(chemical[i+1]-'0');//记录原子个数
            i++;
        }
        for(int m=0;m<n;m++){
            if(strcmp(element,elements[m])==0){//若前面有相同元素，则计入该原子个数
                num[m]+=number;
                goto break_;
            }
        }
        strcpy(elements[n],element);//没有相同元素则再增加一个元素
        num[n]+=number;
        n++;
        break_:;
    }
    return n;
}

void get_orderly(char **elements,int *num,int elements_total_number){
    if(elements==NULL||num==NULL){
        exit(1);
    }
    int flag=1;//用来判断排序是否完成，若最后值为0，则排序完成
    while (flag==1){
        flag=0;
        char *ctemps;
        int itemps;//用于交换的中间量
        for(int i=0; i < elements_total_number - 1; i++){//冒泡排序
            if(strcmp(elements[i],elements[i+1])>0){
                ctemps=elements[i];
                elements[i]=elements[i+1];
                elements[i+1]=ctemps;
                itemps=num[i];
                num[i]=num[i+1];
                num[i+1]=itemps;
                flag=1;
            }
        }
    }
}

注意：输出有顺序要求，最后结果要按照ASCII码进行排序。这个排序是每个字母依次比较，像是Na和Mg大小比较的话，因为ASCII码中N>M，所以Na>Mg，Mg要排在Na前面。如果首字母相同，则比较下一个字母，只要能比较出一个就终止比较。技巧：我这里使用了strcmp()函数，这个函数定义在<string.h>头文件中，可以用来比较字符串大小，比较方法和我上面所说的相同。这个函数小于，等于，大于分别返回负数，0，正数。

思路：首先对于新元素进行记录，并将元素后没有数字情况特殊判断。之后的元素要判断是否在之前有过记录，如果有，则需要将数量加在之前的相同元素所对于的数量上。在对于元素数量统计好之后，进行排序即可。这题其实也可以只认为元素符合最多两个字母来计算，应该也可以AC。