原文地址: http://blog.csdn.net/qq_22717679/article/details/51178927
线性模型 - Linear models
举个例子引入,银行发放信用卡问题。银行掌握了某顾客的资料,包括年龄、性别、年薪、年工作时间、信用贷款等等,现在银行需要知道:
要不要发信用卡给该顾客?——Binaryclassification y=0/1
给该顾客多少信用额度?——Linear regression y∈R
该顾客透支信用额度无法还款的可能性有多大?——Logistic regression y∈[0,1]
- PLA/pocket
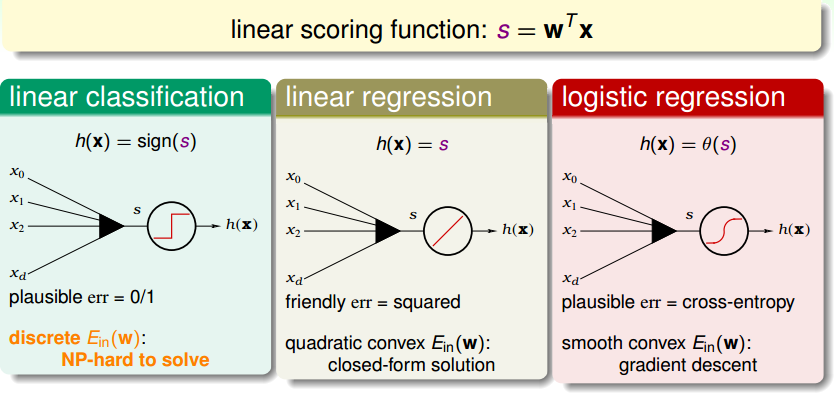
For binary classification解决是非问题
Perceptron是二类线性分类模型:输入向量X的每一个分量都对应一个权重w(也就是每个因素对最后输出的重要程度),线性组合后得到一个score,根据设定的阈值输出y,即score大于阈值y取+1,小于阈值y取-1
Perceptron learning algorithm是训练出最佳Perceptron的方法,也就是得到使 Ein(w)min的w:由一组样本训练出可将所有样本点正确分类的Perceptron,思路是由一个初始分类(二维是直线)开始,寻找这个分类分错的样本点,修正该分类(线向该点方向偏移),直至找不出错误分类样本点
PLA是迭代的过程,若训练样本线性可分,则PLA能够停下来(可证);若不是线性可分,这就是一个NP-hard问题,一个解决方法是pocket口袋算法,每次迭代比较口袋里和手里的分法,将较好的放在pocket里暂存,直至循环次数足够多停止,这样比较贪心的得到一个不错的w
参考:http://blog.csdn.net/bingduanlbd/article/details/24468885
- Linearregression 线性回归
与二值分类问题相比,线性回归过程省去了阈值判断步骤:输入向量X的每一个分量都对应一权重w,线性组合后得到一个结果,直接将score作为y值输出,求最佳权重向量w
线性回归通常用squared error作为错误衡量,回归过程也就是寻找w(直线/平面/超平面),使得输入数据的残差最小的过程;由于Ein(w)是连续可微的凸函数,求解其微分为零的点找到曲线的“谷底”,且式子直接可解,于是“一步登天”得到解








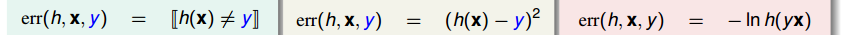
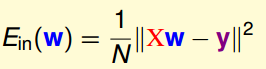
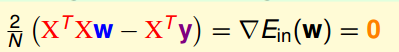














 2605
2605

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








