求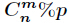
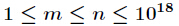
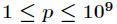
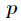
这个问题有个叫做Lucas的定理,定理描述是,如果
那么得到
这样然后分别求,采用逆元计算即可。
题目:http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=4536
题意:给一个集合,一共
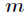
分析:典型的隔板法,最终答案就是
题目:http://acm.hdu.edu.cn/showproblem.php?pid=4373
题意: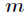


是第一种类型,求总的循环的次数对364875103取余的结果。
分析:首先可以看出,每一个第一类循环都是一个新的开始,与前面的状态无关,所以可以把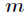
同的部分,每一个部分由第一类循环开始,最终结果相乘即可。剩下的就是第二类循环的问题,假设一个
层循环,最大到
(1)只有一层,则循环次数为
(2)只有前两层,则循环次数为
(3)只有前三层,则循环次数为
由此得到结论:第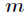
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
#include<algorithm>
#define ll long long
void gcd(ll a,ll b,ll &d,ll &x,ll &y)
{
if(b==0) { d=a; x=1; y=0; return; }
gcd(b,a%b,d,y,x); y-=a/b*x;
}
ll powmod(ll a,ll n,ll m)
{
ll res=1; for(a%=m;n;n/=2,a=a*a%m) if(n&1) res=res*a%m; return res;
}
ll inv(ll a,ll n)
{
ll x,y,d; return powmod(a,n-2,n)%n; //gcd(a,n,d,x,y); return (x+n)%n;
}
const ll mod=364875103;
const ll mod1=97;
const ll mod2=3761599;
const int N=200100;
ll fac1[N+4],fac2[mod2+2];
void facinit(ll fac[],ll mod)
{
fac[0]=1;
for(int i=1;i<mod;i++) fac[i]=fac[i-1]*i%mod; //,r[i]=powmod(fac[i],mod-2,mod);
}
ll C(ll n,ll m,ll fac[],ll mod)
{
if(n<m) return 0;
return fac[n]*inv(fac[n-m]*fac[m],mod)%mod;
}
ll CC(ll n,ll m,ll fac[],ll mod)
{
if(m==0) return 1; ll p=mod;
return C(n%p,m%p,fac,mod)*CC(n/p,m/p,fac,mod);
}
ll n,m,k;
int main()
{
facinit(fac1,mod1); facinit(fac2,mod2);
ll inv2=mod2*inv(mod2,mod1); ll inv1=mod1*inv(mod1,mod2);
int re; cin>>re; int ca=1;
while(re--)
{
cin>>n>>m>>k; ll a[43];
for(int i=0;i<k;i++) cin>>a[i]; a[k]=m;
ll ans=1;
for(int i=0;i<k;i++)
{
ll t1=CC(a[i+1]-a[i]+n-1,a[i+1]-a[i],fac1,mod1);
ll t2=CC(a[i+1]-a[i]+n-1,a[i+1]-a[i],fac2,mod2);
ll tmp=(t1*inv2+t2*inv1)%mod;
ans=ans*tmp%mod;
}
printf("Case #%d: %I64d\n",ca++,ans);
}
}
题目:http://acm.hdu.edu.cn/showproblem.php?pid=4349
题意:
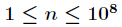
分析:其实组合数判断奇偶性有一个优美的结论
如果

当然本题要判断的组合数很多,所以不能用上述结论,只能另辟蹊径。由于是判断奇偶性,那么就是判断
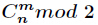

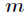
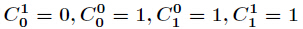

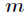
这样我们可以不用管


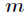
或1,其结果都是1,这样答案就是:1<<(










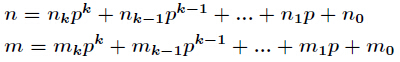
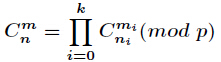
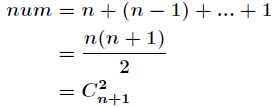
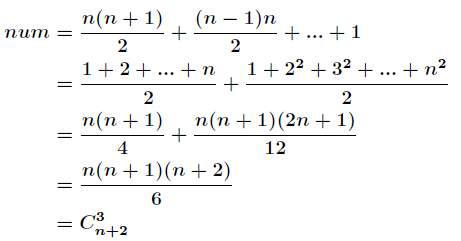
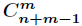














 133
133

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








