一点数论——从零开始的莫比乌斯反演笔记（简单易懂）

1.前置知识

(1) 数论分块

之前写过专门说这个的了，传送门
大致是求形如
$$\sum _{i=1}^n\lfloor \frac{n}{i}\rfloor$$

代码也很短，主要是：

for(int l=1,r;l<=n;l=r+1)
{
	r=n/(n/l);
	ans+=(r-l+1)*(n/l);
}

（2）莫比乌斯函数

这是来自百度百科的解释：

简单来说就是

1. 当$n=1$时，$\mu (n)=1$
2. $n$分解质因数后，没有幂次大于平方的质因子,$\mu (n)=(-1{)}^k$
3. 只要当$n$含有任何质因子的幂次大于等于2,$\mu (n)=0$.

(3)狄利克雷卷积之常用性质1（非常重要/常用）

$$\mu \ast 1=ϵ$$

对于任意正整数n
$$\sum _{d|n}\mu (d)=ϵ(n)=[n=1]$$
$[n=1]$表示只有当$n=1$成立时，返回值为1否则，值为0。

我们在莫比乌斯反演中套路是这样的：
$$[gcd(i,j)=1]=\sum _{d|gcd(i,j)}\mu (d)$$

(2) 狄利克雷卷积之常用性质2

$$\varphi \ast 1=Id$$

其中$Id$函数表示$I{d}_k(x)=x^k$

其实还有如下结论：

以及一条还不知道有啥用的公式：
$$\sum _{d|n}\frac{\mu (d)}{d}=\frac{\varphi (n)}{n}$$

2.莫比乌斯反演

咱们终于进入正题啦！

定理

设$f(n)$和$g(n)$是定义在非负整数集合上的两个函数，并且满足条件：
$$f(n)=\sum _{d|n}g(d)$$

那么有：
$$g(n)=\sum _{d|n}\mu (d)f(\lfloor \frac{n}{d}\rfloor )$$

证明

方法一 数论推导

$$\sum _{d|n}\mu (d)f(\frac{n}{d})=\sum _{d|n}\mu (d)\sum _{k|\frac{n}{d}}g(k)=\sum _{k|n}g(k)\sum _{d|\frac{n}{k}}\mu (d)=g(n)$$

用${\sum }_{k|\frac{n}{d}}g(k)$代替$f(\frac{n}{d})$,然后变换求和顺序，最后一步的依据是
$$\sum _{d|n}\mu (d)=[n=1]$$




方法二 狄利克雷卷积推导

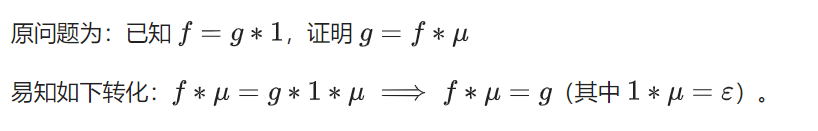
当然莫比乌斯反演还有另外一种形式：
如果有
$$f(n)=\sum _{n|d}g(d)$$
那么有
$$g(n)=\sum _{n|d}\mu (\frac{d}{n})f(d)$$

3.例题

我一看到那个需要设函数的莫比乌斯反演公式就烦躁，所以下面的推导决定不用那个公式。开始看例题前我们先回忆下这个公式：
$$[gcd(i,j)=1]=\sum _{d|gcd(i,j)}\mu (d)$$
(以下例题全部默认$n<m$,且所有分式都是向下取整！！！)

例题1

求
$$\sum _{i=1}^n\sum _{j=1}^m[gcd(i,j)=1]$$

我们直接套公式就好啦：
$$\begin{gathered} =\sum _{i=1}^n\sum _{j=1}^m\sum _{d|gcd(i,j)}\mu (d) \\ =\sum _{d=1}^n\mu (d)\sum _{i=1}^{\frac{n}{d}}\sum _{j=1}^{\frac{m}{d}} \\ =\sum _{d=1}^n\mu (d)\ast \lfloor \frac{n}{d}\rfloor \ast \lfloor \frac{m}{d}\rfloor \end{gathered}$$
我们会注意到后面那块是可以数论分块$O(\sqrt[]{n})$处理的

例题2

求
$$\sum _{i=1}^n\sum _{j=1}^m[gcd(i,j)=k]$$
解法：
$$\begin{gathered} =\sum _{i=1}^n\sum _{j=1}^m[gcd(\frac{i}{k},\frac{j}{k})=1] \\ =\sum _{i=1}^{\frac{n}{k}}\sum _{j=1}^{\frac{m}{k}}[gcd(i,j)=1] \end{gathered}$$

例题3

求：

$$\sum _{i=1}^n\sum _{j=1}^{m}ij[gcd(i,j)=k]$$
解：
$$\begin{gathered} =\sum _{i=1}^n\sum _{j=1}^{m}ij[gcd(\frac{i}{k},\frac{j}{k})=1] \\ =\sum _{i=1}^{\frac{n}{k}}\sum _{j=1}^{\frac{m}{k}}ij[gcd(i,j)=1]k^2 \\ =\sum _{i=1}^{\frac{n}{k}}\sum _{j=1}^{\frac{m}{k}}ij{k}^2\sum _{d|gcd(i,j)}\mu (d) \\ =\sum _{d=1}^n\mu (d)d^2\sum _{i=1}^{\frac{n}{kd}}\sum _{j=1}^{\frac{m}{kd}}ij{k}^2 \end{gathered}$$

这里要说一下

为什么会多一个 $d^2$和$k^2$ 啊？

因为求和上下线限变了之后，gcd变成了可以用套路式换掉的样子，但是中间的$ij$这一项缩小到了原来的$\frac{1}{k^2}$倍，所以需要乘回去。$d^2$同理。

例题4

求
$$\sum _{i=1}^n\sum _{j=1}^{m}lcm(i,j)$$

解：
$$\begin{gathered} =\sum _{i=1}^n\sum _{j=1}^m\frac{ij}{gcd(i,j)} \\ =\sum _{d=1}^n\sum _{i=1}^n\sum _{j=1}^m\frac{ij}{d}[gcd(i,j)=d] \\ =\sum _{d=1}^n\sum _{i=1}^{\frac{n}{d}}\sum _{j=1}^{\frac{m}{d}}i\ast j\ast d[gcd(i,j)=1] \\ =\sum _{d=1}^n\sum _{i=1}^{\frac{n}{d}}\sum _{j=1}^{\frac{m}{d}}i\ast j\ast d\sum _{k|gcd(i,j)}\mu (k) \\ =\sum _{d=1}^{n}d\sum _{k=1}^{\frac{n}{d}}\mu (k)\sum _{i=1}^{\frac{n}{dk}}\sum _{j=1}^{\frac{m}{dk}}i\ast j\ast k^2 \end{gathered}$$

4.练习题

T1 ZAP-Queries

求
$$\sum _{i=1}^n\sum _{j=1}^m[gcd(i,j)=k]$$
解：
$$\begin{gathered} =\sum _{i=1}^{\frac{n}{k}}\sum _{j=1}^{\frac{m}{k}}[gcd(i,j)=1] \\ =\sum _{i=1}^{\frac{n}{k}}\sum _{j=1}^{\frac{m}{k}}\sum _{d|gcd(i,j)}\mu (d) \\ =\sum _{d=1}^{\frac{n}{k}}\mu (d)\sum _{i=1}^{\frac{n}{kd}}\sum _{j=1}^{\frac{n}{kd}} \\ =\sum _{d=1}^{\frac{n}{k}}\mu (d)\lfloor \frac{n}{kd}\rfloor \lfloor \frac{m}{kd}\rfloor \end{gathered}$$
先线性筛一下莫比乌斯函数，然后用一下整除分块就好啦

ACcode:

#include<bits/stdc++.h>
#define LL long long
using namespace std;
const int N = 50100;

bool pd[N];
int n,m,k,mu[N],tot=0,pr[N];
LL sum[N];
void pre(int n)
{
	pd[1] = true;
	mu[1] = 1;
	for(int i=2;i<=n;i++)
	{
		if( pd[i]==false )
		{
			tot++;
			pr[tot] = i;
			mu[i] = -1;
		}
		for(int j=1;j<=tot&&i*pr[j]<=n;j++)
		{
			pd[ i*pr[j] ] = true;
			if( i%pr[j]==0 )
			{
//				mu[ i&pr[j] ] = 0;
				break;
			}
			else mu[ i*pr[j] ] = -mu[i];
		}
	}
	for(int i=1;i<=n;i++) sum[i] = sum[i-1] + mu[i];
}
LL ans = 0;
void solve()
{
	scanf("%d %d %d",&n,&m,&k);
	if( n>m ) swap(n,m);
	ans = 0;
	n /= k;
	m /= k;
	for(int l=1,r;l<=n;l=r+1)
	{
		r = min( n/(n/l) , m/(m/l) );
		ans += 1ll*(sum[r]-sum[l-1])*(n/l)*(m/l);
	}
	printf("%d\n",ans);
}

int main()
{
	//freopen("in.txt","r",stdin);
	pre(50000);
	int t;
	cin>>t;
	while( t-- )
	{
		solve();
	}
	return 0;
}

T2 Problem b

求：
$$\sum _{i=a}^b\sum _{j=c}^d[gcd(i,j)=k]$$
这题跟上题一模一样，只是多了个容斥。
$ans=ans((1,b),(1,d))-ans((1,b),(1,c-1))-ans((1,a-1),(1,d))+ans((1,a-1),(1,c-1))$

ACcode:

#include<bits/stdc++.h>
#define LL long long
#define N 50100
using namespace std;

int sum[N],ans;
int pr[N],tot = 0,mu[N],a,b,c,d,k;
bool pd[N];


void get_mu(int n)
{
	pd[1] = true;
	mu[1] = 1;
	for(int i=2;i<=n;i++)
	{
		if( pd[i]==false )
		{
			pr[++tot] = i;
			mu[i] = -1;
		}
		for(int j=1;j<=tot&&i*pr[j]<=n;j++)
		{
			pd[ i*pr[j] ] = true;
			if( i%pr[j]==0 ) break;
			else mu[ i*pr[j] ] = -mu[i];
		}
	}
	for(int i=1;i<=n;i++) sum[i] = sum[i-1] + mu[i];
}

LL cal(int n,int m)
{
	LL s = 0;
	n /= k;
	m /= k;
	if( n>m ) swap(n,m);
	for(int l=1,r;l<=n;l=r+1)
	{
		r = min( n/(n/l) , m/(m/l) );
		s += (LL)(sum[r]-sum[l-1]) * (LL)(n/l) * (LL)(m/l);
	}
	return s;
}

void solve()
{
	scanf("%d %d %d %d %d",&a,&b,&c,&d,&k);
	ans = cal( b,d ) - cal( a-1,d ) - cal( b,c-1 ) + cal( a-1,c-1 );
	printf("%d\n",ans);
}

int main()
{
	int t;
	cin>>t;
	get_mu(50000);
	while( t-- ) solve();
	return 0;
}

T3 [国家集训队]Crash的数字表格

求：
$$\sum _{i=1}^n\sum _{j=1}^{m}lcm(i,j)$$

解：
$$\begin{gathered} =\sum _{i=1}^n\sum _{j=1}^m\frac{ij}{gcd(i,j)} \\ =\sum _{d=1}^n\sum _{i=1}^n\sum _{j=1}^m\frac{ij}{d}[gcd(i,j)=d] \\ =\sum _{d=1}^n\sum _{i=1}^{\lfloor \frac{n}{d}\rfloor }\sum _{j=1}^{\lfloor \frac{m}{d}\rfloor }i\ast j\ast d[gcd(i,j)=1] \\ =\sum _{d=1}^n\sum _{i=1}^{\lfloor \frac{n}{d}\rfloor }\sum _{j=1}^{\lfloor \frac{m}{d}\rfloor }i\ast j\ast d\sum _{x|gcd(i,j)}\mu (x) \\ =\sum _{d=1}^n\sum _{x=1}^{\lfloor \frac{n}{d}\rfloor }\mu (x)\ast x^2\sum _{i=1}^{\lfloor \frac{n}{dx}\rfloor }\sum _{j=1}^{\lfloor \frac{m}{dx}\rfloor }i\ast j \\ =\sum _{d=1}^n\sum _{x=1}^{\lfloor \frac{n}{d}\rfloor }\mu (x)\ast x^2\ast \frac{\lfloor \frac{n}{dx}\rfloor (1+\lfloor \frac{n}{dx}\rfloor )}{2}\ast \frac{\lfloor \frac{m}{dx}\rfloor (1+\lfloor \frac{m}{dx}\rfloor )}{2} \end{gathered}$$

Accode:

#include<bits/stdc++.h>
#define LL long long
#define N 10010000
using namespace std;
const LL M = 20101009;
int pr[N],tot=0,mu[N];
LL sum[N];
bool pd[N];
void get_mu(int x)
{
	pd[1] = false;
	mu[1] = 1;
	for(int i=2;i<=x;i++)
	{
		if( pd[i]==false )
		{
			tot++;
			pr[tot] = i;
			mu[i] = -1;
		}
		for(int j=1;j<=tot&&i*pr[j]<=x;j++)
		{
			pd[ i*pr[j] ] = true;
			if( i%pr[j]==0 ) break;
			mu[ i*pr[j] ] = -mu[i];
		}
	}
	for(int i=1;i<=x;i++)
	{
		sum[i] = ( sum[i-1] + 1LL*i*i%M*mu[i]%M )%M;
	}
}


LL cal(int x,int y) 
{
    return (1LL*x*(x+1)/2%M)*(1LL*y*(y+1)/2%M)%M;
}

LL func(int n,int m)
{
	LL ans = 0;
	for(int l=1,r;l<=n;l=r+1)
	{
		r = min( n/(n/l),m/(m/l) );
		ans = ( ans + ( sum[r]-sum[l-1] )*cal(n/l,m/l)%M )%M;
	}
	ans = (ans%M+M)%M;
	return ans;                                    
}

void solve()
{
	int n,m;
	LL ans = 0;
	scanf("%d %d",&n,&m);
	if( n>m ) swap(n,m);
	get_mu(n);
	for(int l=1,r;l<=n;l=r+1)
	{
		r = min( n/(n/l) , m/(m/l) );
		ans = ( ans + 1LL*( r-l+1 )*( r+l )/2%M * func(n/l,m/l)%M )%M;
	}
	ans = (ans+M)%M;
	printf("%lld\n",ans);
}


int main()
{
	solve();
	return 0;
}