李宏毅学习笔记3.Gradient Decent

复习

先是复习之前课程中梯度下降的过程，回顾了大概的符号表示（Notation），这里注意上下标。
黄色框框是向量的表示方式。

黄色部分就是梯度。作图表示出来就变成下面这个图：

复习完毕就进入下一个环节：

梯度下降法的一些小技巧Tips

Tip 1: Tuning your learning rates

当只有两个参数的时候，可以画出左边的损失函数图形，然后在图上可以给出下面几个LR（Learning Rate）的建议：
1、LR太小（蓝色），需要很久才会到达最优解，就是不容易收敛；
2、LR较大（绿色），接近最优解处会发生震荡；
3、LR非常大（黄色），直接飞出去，越算损失值越大；
只有LR设置适合的值（红色）才能比较合适的收敛。
当有多个参数的时候，可以画出右边的图形，横坐标是迭代次数，纵坐标是损失函数的值。这里面的颜色和上面描述的颜色相对应。
正确的做法：
在做梯度下降的时候，需要把右边这个图画出来，并且观察前几次迭代情况，确保损失函数值是减少的
然后是对自适应LR的梯度下降算法的一些思想：

自适应调整LR的思想

1、开始的时候离最优解比较远，LR可以大一点，步长大一点，经过几次迭代后，靠近最优解，LR可以变小一点，步长小一点。例如按图中的公式：${\eta }_t=\frac{\eta }{\sqrt{t+1}}$，随时间变化，步长越来越小
2、不同的参数使用不同的LR，典型的算法是Adagrad：

PS：Vanilla是原版的意思（感谢B站弹幕）。
$\sigma$对于每个参数都是相互独立的（原话是：$\sigma$参数dependent的参数，$\eta$是时间dependent的参数），下面看一个例子：

g0代表损失函数在w0处的偏导，以此类推。。。
PS： root mean square是均方根

计算出来σ带入之前的梯度计算公式，得到最终形态（上图）。注意，这里t+1这项消掉了。
这个方法的缺点：整体更新会越来越慢，原因是它考虑了time dependent。
然后有一个问题，从下图可以看出来：

和原版梯度下降不一样（原版是梯度越大，步长越大），Adagrad的分母越大的同时，分子也越大。
说人话：本来如果梯度越大，那么按理来说应该更新的步长越大，但是由于分母也有一个梯度项，因此，会现在更新的步长变大，也就是分内工作梯度突然爆炸或者消失。
这个体现了Adagrad算法中考虑的是反差的效果如何，反差在ppt上也给出了例子：

上图是反差特别大和反差特别小的例子，也就是简单粗暴的从分母上看到反差的效果，理论上老师给出了进一步解释。

Adagrad步长的理解

单个变量

当只有一个参数的时候，步长其实是和导数的大小有关，导数越大，说明距离最优解越远，这个时候步长应该越长，而且最优步长是和导数成正比：
例如有一个二次函数：
$$y=a{x}^2+bx+c$$
最小值为：$-\frac{b}{2a}$

其导数为：
$$|\frac{\partial y}{\partial x}|=|2ax+b|$$

如果随机从某个位置$x_0$处开始用梯度下降进行往最小值走，那么步长应该多大合适？
应该是$x_0$到最小值的距离，这样一步就到位：

这个距离计算就是：$|x_0+\frac{b}{2a}|=\frac{|2a{x}_0+b|}{2a}$
可以看到，分子就是在$x_0$的导数，意味这个时候导数越大，距离最小值越远。
上面的例子只有一个变量x，但是有多个参数的时候这个结论就不成立了。

蓝色部分切一刀得到$w_1$的损失函数形状，形状扁，变化较小；
绿色部分切一刀得到$w_2$的损失函数形状，形状尖，变化较大。
只看w1，a处的导数比b处的大，所以a比b离最优解远
只看w2，c处的导数比d处的大，所以c比d离最优解远
联合起来看，虽然a比c处的导数大，但是c比a离最优解近
所以进一步推导

多个变量

在之前的一个变量的例子中，分母其实是二次微分。也就是最佳步长为：


其实最优步长要考虑二次导数
在$w_1$上，由于曲线形状比较平滑，所以二次导数比较小
在$w_2$上，由于曲线形状比较尖，所以二次导数比较大
这个事情与之前的Adagrad公式联系起来

其实当参数比较多或者式子比较复杂的时候二次导数比较难求，Adagrad算法其实是估算的（图中问号代表的就是估算的意思，估算的方法就是上图中的下半部分，有点类似拟牛顿法），估算的原理就是下面两个例子。

Tip 2: Stochastic Gradient Descent

Stochastic 是随机的意思

原版梯度下降算法在求梯度的时候有一个求和操作，把所有的训练样本的损失值计算出来求和。
随机梯度算法SGD只选取一个训练样本，可以看到公式$L^n$里面没有求和符合，而且L多了上标n
下面是老师给的算法可视化比较实例：

左边走一步，右边走了20步。（原话：天下武功，唯快不破！）

Tip 3: Feature Scaling

当特征取值范围相差较大的时候，需要对特征进行scaling（缩放？）处理。

接下来看实例

左下角由于改变$w_2$对y的影响比较大，损失函数所以在$w_2$方向上比较sharp（原话，按之前例子中的横截面来看应该是比较尖），这种形状的用Adagrad的LR才能搞定，也就是不同参数使用不同的LR
缩放以后就变圆，从图上红色梯度下降的过程可以看到，做了缩放后无论从哪里出发，都是指向圆心，比较有效率。
缩放（归一化normalization）有很多种，老师给出了其中一种：

看弹幕解释说这个方法实际是算Z Score，先记下来，有空再验证，或者有人知道欢迎评论。

梯度下降的推导

下面就是准备进行推导，老师非常贴心的给出了 Warning of Math ！
推导前，问了一个问题：

答案是不一定update会使得损失函数变小，过程中是有可能变大的（例子可以看本章tip 1中的例子，当LR很大的时候就会反而变大）。
然后是正式推导：

推倒思路

假设θ又两个变量
如下图所示，给定一个点${\theta }_0$，我们虽然不能找出该点对于最优解的梯度方向，但是可以很容易在一个小的范围内（红圈圈）找出一个最小值作为梯度下降方向。

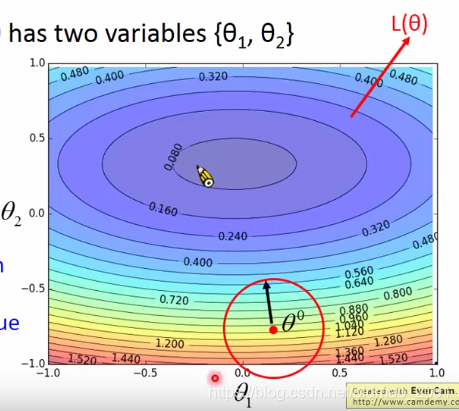
图中的红色圈就代表一个小的范围，箭头就是我们找到这个范围内的最小值并指向该最小值的梯度下降方向，然后把位置挪到${\theta }_1$。

接下来再画一个圆圈

再在这个新圈圈里面找到最小值，并更新中心点参数，到达${\theta }_2$这个地方

PS：那个箭头上的红点是老师讲解的鼠标。


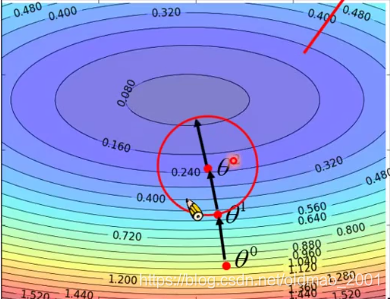
然后继续更新中心位置。
现在的问题是：如何在在这个红色圈圈里面找到最小的损失函数值？
答曰：要从泰勒级数讲起。。。。

泰勒级数

PS：infinitely defferentiable是无穷次可微的。第三行成立的原因是：当x接近x0的时候x-x0要远远大于(x-x0)的平方，所以后面的项都可以忽略不计了
举个栗子：

以上是sin(x)的泰勒展开式，然后考虑不同的项的图形如下：

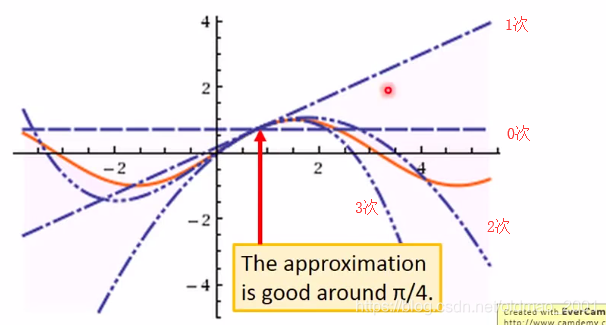
橙色那条就是sin(x)的图像，可以看到在π/4的地方，考虑到1次项已经接近sin(π/4)的值了。
以上是单个参数的泰勒级数
多个参数的情况如下：


注意，虽然上式总的偏微分看上去很复杂，实际上计算出来是常数项（老师说的）
回到之前的梯度下降思路中求小圈圈附近最小的问题

计算

可以借用泰勒级数把损失函数展开，并且只需要考虑到1次项，由于上图中偏导求出来都是常数，可以用s，u，v三个符号进行替换简化表示，最后得到左下角的损失函数的最终形式，小圈圈内求最小变成了：

这里有一个约束，红色圈圈的中心是a和b，，这个圈圈的半径是d，则有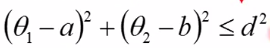


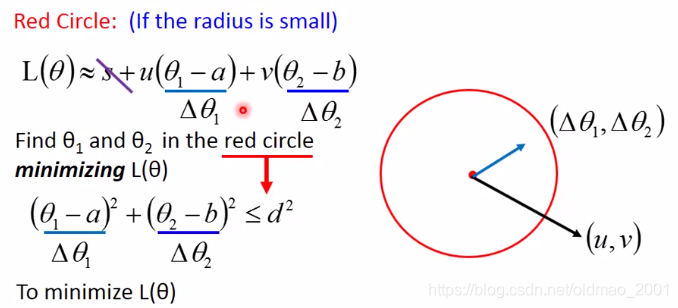
解释一下，把两个括号里面的东西用$\Delta {\theta }_1$和$\Delta {\theta }_2$表示，求函数最小，s可以不用考虑（因为s和变量$\theta$无关），那么整个函数可以看做右图的两个向量的内积，那最小化两个向量的内积，就是要他们两个反向就好，把$\Delta {\theta }_1$和$\Delta {\theta }_2$转到u和v的反向，如：

并且把$\Delta {\theta }_1$和$\Delta {\theta }_2$的向量长度增大到圈圈的半径长度（就是最大咯）。用数学表示就如下图

箭头右边是吧$\Delta {\theta }_1={\theta }_1-a$和$\Delta {\theta }_2={\theta }_2-b$带入左边整理后得到，再把前面u和v带回来

PS：ppt上偏导L写成C了，用红色改一下。
这个式子就是梯度下降的形式，ab是初始位置，减去LR乘以偏导。老师补充说，这个推导成立的条件是损失函数可以用泰勒级数展开，而泰勒级数展开的条件是圈圈足够小，上式总LR（就是$\eta$）是和半径成正比的，所以结论是当LR够小（小才能泰勒展开，不然展开不精确，那个约等于的式子不成立）的时候，才能保证每次梯度更新都使得损失函数变小。
当然我们也可以考虑泰勒展开的2次项，例如牛顿法，这个时候的LR就可以取得大一些。但是在做DL的时候弄到2次项（2次导数）会大大增加计算量，不划算

梯度下降其他缺陷

除了容易卡在局部最小值处之外，还有两个比较容易被忽视的缺点。
然后老师秀了一把帝国时代和我的世界。