论文:https://mediatum.ub.tum.de/doc/1292048/file.pdf
在文本识别模型CRNN中,一张包含单行文本的图片输入模型经过CNN、LSTM后输出大小的feature map, 假设T=25表示时间序列长度,m=26代表需要识别的字符集的大小(假设只识别小写英文字母),对每一个时间步
接softmax后就得到识别结果的概率分布,对每一个时间步
满足
,但是在与label进行loss计算时需要先将图片中的每一个字符与label对齐,这就需要对单个字进行位置和语义标注,非常麻烦。而且由于字体样式和大小的关系,每列输出并不一定能和每个字符一一对应。ctc loss是一种专门针对这种场景不需要对齐的loss计算方法。接下来介绍ctc loss的具体计算方法
- 空白blank
表示预先定义的模型待识别字符集,因为输入图片中有的位置没有文字,引入空白blank字符,下文以 - 表示blank,LSTM的输出变成
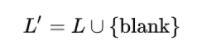
- \(\beta\)变换
定义\(\beta\)变换,LSTM输出首先经过decode,然后经过\(\beta\)变换得到最终结果。\(\beta\)变换包括删除连续重复字符以及blank。例如,当T=12时,下列四个输出经过\(\beta\)变换都变成state。
给定输入,模型输出为
的概率为
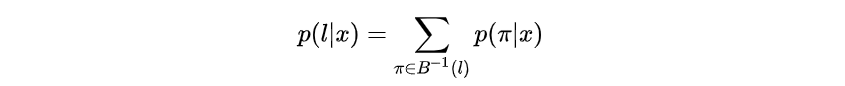
表示所有经过
变换后是
的路径
其中,对于任意一条路径有
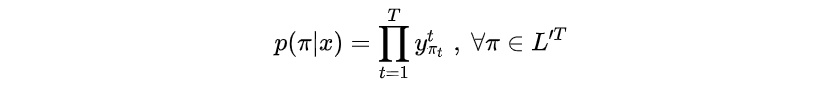
注意这里中的
,下标
表示路径
中的每一个时刻。而上面
的下标表示不同的路径
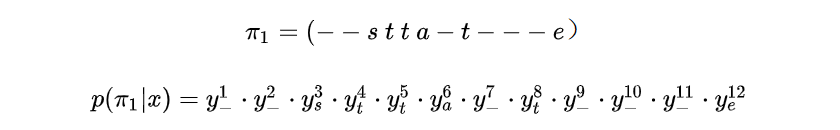
ctc的训练目标是通过梯度调整模型权重
,使得
最大
在实际训练过程中,LSTM的输出特征图T的大小少为几十多则几百,如果遍历每一条路径,复杂度是指数级的,假如识别的是汉字,字符集长度为几千,序列长度
上百,那要遍历
种选择,速度太慢。实际CTC借用了HMM的"前向 - 后向"(forward - backward)算法来计算
,具体过程如下
首先定义路径为在路径
的头尾和每两个字符间插入blank
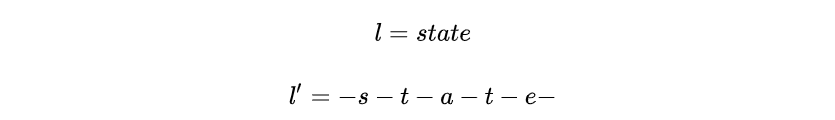
显然
定义所有经变换后结果是
且在
时刻结果为
的路径集和为
,求导
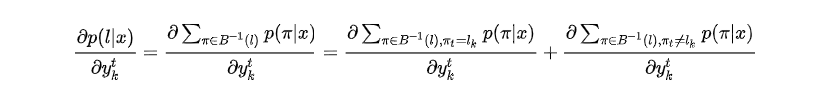
上式中第二项与无关,因此
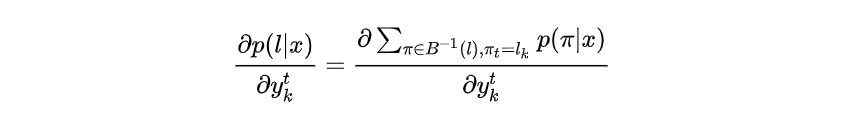
就是恰好与概率
相关的路径,即
时刻都经过
上述的在
时都经过
(此处下标代表路径
的
时刻的字符),所有类似于
经过
变换后结果是
且在
的路径集和表示为

如图,蓝色路径和红色路径分别为上述的和
,
和
可以表示为
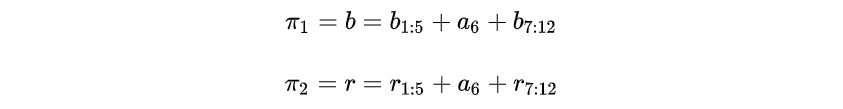
和
可以表示为
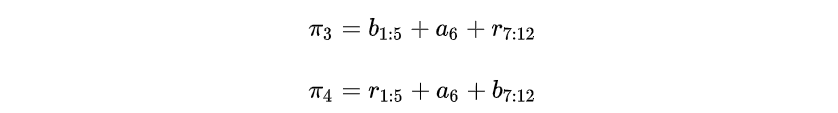
则
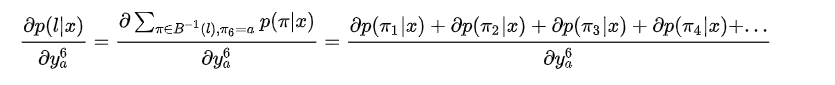

令
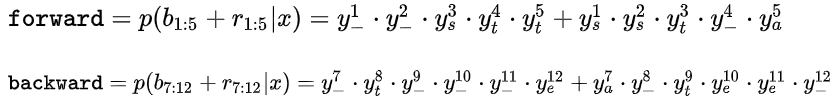
则
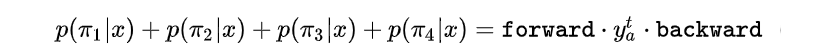
推广一下,所有经过 变换结果为
且
的路径
可以写成如下形式
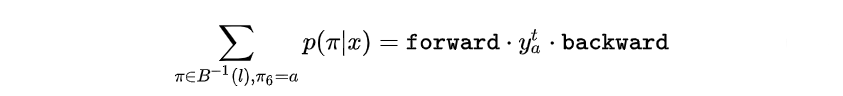
进一步推广, 所有经过 变换结果为
且
的路径
可以写成如下形式
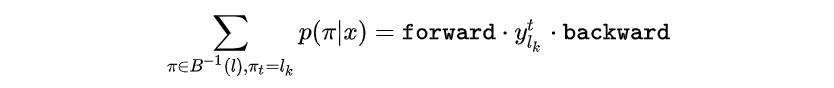
定义前向递推概率和
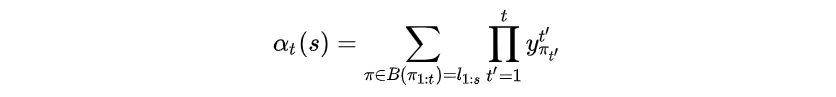
其中 表示路径
的前
个字符经过
变换变成
的前
个字符,
代表了
时刻经过
的所有路径的
的概率和,即前向递推概率和。
当时,路径只能从
或
开始,所以
有如下性质:
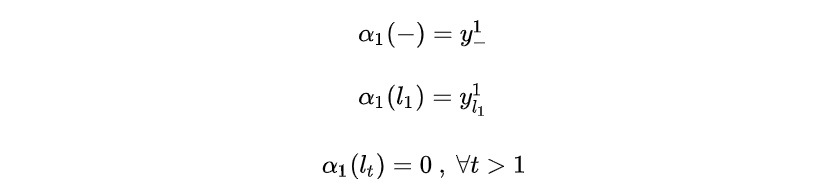
同理,定义后向递推概率和
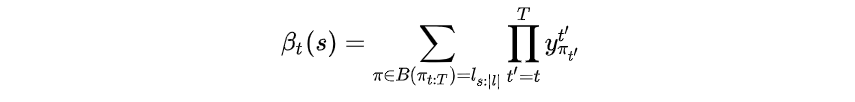
其中表示后
个字符经过
变换为
后半段子路径,
表示
时刻经过
的所有路径的
的概率和,即后向递推概率和。
当时,路径只能以
或
结束,所以
有如下性质:

计算递推loss
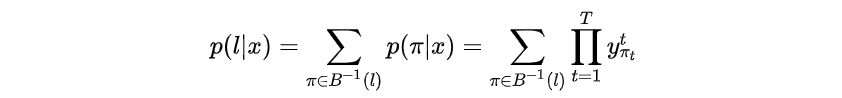
和
相乘有
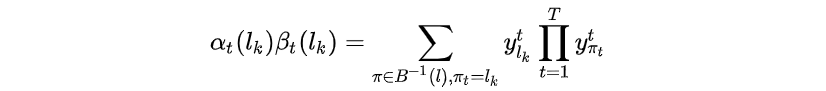
当计算loss对ctc输入即LSTM输出中的某个值的梯度时,只需考虑所有经过
的路径,因此可以得到
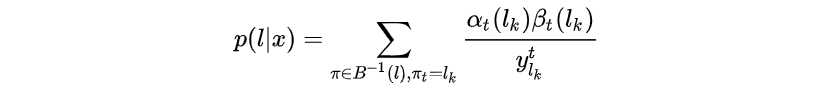
梯度如下
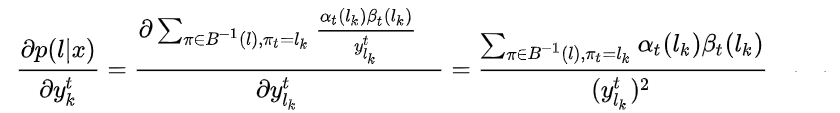
接下来只需计算出和
即可
前面我们给出了的初始条件,即
时,路径只能从
或
开始。
- 当
时刻字符
为
时,
可以由当前
字符
或前一个非空白字符
得到。
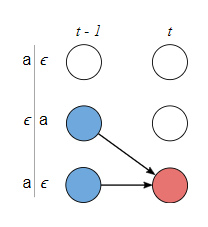
- 当
即当前字符
不是
且和前一个字符相同时,
可以由当前字符
或前一个
字符
得到,如下图所示
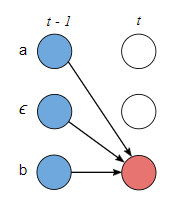
- 当
时刻字符
不是
且
时,
可以由当前字符
、前一个
字符
、前一个非空白字符
得到,如下图所示
由此可以得到递推公式
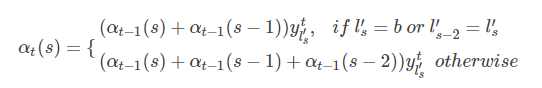
根据初始条件和递推公式,便可以用动态规划计算出,代码如下
import numpy as np
def alpha_vanilla(y, labels): # labels是插入blank后的
T, V = y.shape # T: time step, V: probs
L = len(labels) # label length
alpha = np.zeros([T, L])
# init
alpha[0, 0] = y[0, labels[0]]
alpha[0, 1] = y[0, labels[1]]
for t in range(1, T):
for i in range(L):
s = labels[i]
a = alpha[t - 1, i]
if i - 1 >= 0:
a += alpha[t - 1, i - 1]
if i - 2 >= 0 and s != 0 and s != labels[i - 2]:
a += alpha[t - 1, i - 2]
alpha[t, i] = a * y[t, s]
return alpha同理可得后向递推公式
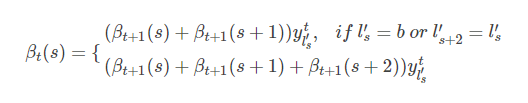
def beta_vanilla(y, labels):
T, V = y.shape
L = len(labels)
beta = np.zeros([T, L])
# init
beta[-1, -1] = y[-1, labels[-1]]
beta[-1, -2] = y[-1, labels[-2]]
for t in range(T - 2, -1, -1):
for i in range(L):
s = labels[i]
a = beta[t + 1, i]
if i + 1 < L:
a += beta[t + 1, i + 1]
if i + 2 < L and s != 0 and s != labels[i + 2]:
a += beta[t + 1, i + 2]
beta[t, i] = a * y[t, s]
return beta计算梯度
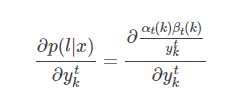
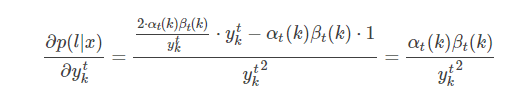
求导中,分子第一项是因为中分别包含一个
项,其它项均为与
无关的常数。
另外,中可能包含多个
字符,因为计算的梯度要进行累加。例如
,
,即求
输出中
处的
字符的梯度,这里的
可能通过
变换成
中的第一个
也可能变换成第二个
。因此,最终的梯度计算结果为
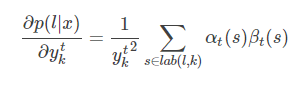
其中,
一般我们优化似然函数的对数,梯度如下
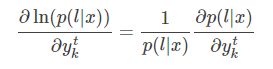
其中,可直接求得
梯度计算代码如下
def gradient(y, labels):
T, V = y.shape
alpha = alpha_vanilla(y, labels)
beta = beta_vanilla(y, labels)
p = alpha[-1, -1] + alpha[-1, -2]
grad = np.zeros([T, V])
for t in range(T):
for s in range(V):
lab = [i for i, c in enumerate(labels) if c == s]
for i in lab:
grad[t, s] += alpha[t, i] * beta[t, i]
grad[t, s] /= y[t, s] ** 2
grad /= p
return grad






















 4011
4011











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










