《深度强化学习》第二章-蒙特卡洛方法-读书笔记

1. 随机变量记作$X$,观测值记作$x$,观测值只是数字而已，没有随机性,如$P(X=0)=\frac{1}{2}$中为大写；
2. 给定随机变量$X$,它的累积分布函数（即概率分布函数）（CDF）是函数$F_X:R\to [0,1]$,定义为：
   $$F_X(x)=P(X\le x)$$
3. 对于离散概率分布，有概率质量函数$p(x)$,假设随机变量$X$取值范围是集合$\chi$
   则有： $$\sum _{x\in \chi }p(x)=1$$ ,$X$的概率质量函数为$p(\cdot )$,则函数$h(X)$关于变量$X$的期望是
   $$E_{X\sim p(\cdot )}[h(X)]=\sum _{x\in \chi }p(x)\cdot h(x)$$
4. 对于连续概率发布，有概率密度函数$p(x)$,随机变量$X$的取值范围$\chi$是连续集合，则有：$${\int }_{-\infty }^{x}p(u)du=F_X(x)=P(X\le x)$$$${\int }_{-\infty }^{+\infty }p(u)du=1$$,$X$的概率密度函数为$p(\cdot )$,则函数$h(X)$关于变量$X$的期望是
   $$E_{X\sim p(\cdot )}[h(X)]={\int }_{\chi }p(x)\cdot h(x)dx$$
   

例一、近似$\pi$值

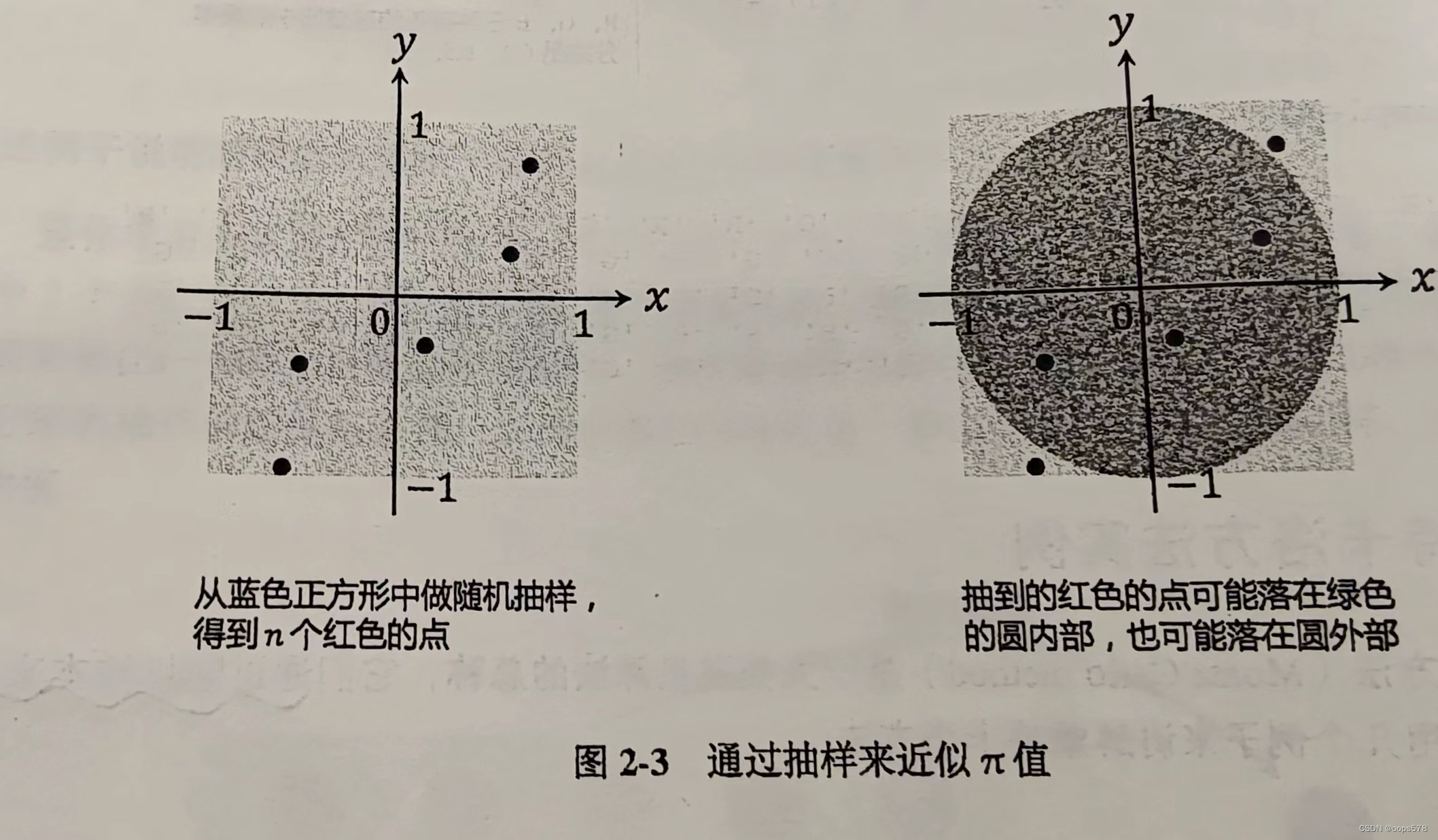
import torch
m = 0
n = 100000

for i in range(n):
    x,y = 2*torch.rand(1)-1,2*torch.rand(1)-1
    if  torch.pow(x,2)+ torch.pow(y,2) <= 1:
        m = m+1

pi = 4 * m / n
print(pi)

输出：3.13528

# 2.2节，蒙特卡洛近似计算圆周率。
import numpy as np

def approxiate_pi(n: int):
    # 在[-1, 1] x [-1, 1]的空间中随机取n个点。
    x_lst = np.random.uniform(-1, 1, size=n)
    y_lst = np.random.uniform(-1, 1, size=n)
    # 统计距离圆心距离在1以内的点。
    m = 0
    for x, y in zip(x_lst, y_lst):
        if x ** 2 + y ** 2 <= 1:
            m += 1
    # 近似计算圆周率。
    pi = 4 * m / n
    return pi


if __name__ == "__main__":
    pi = approxiate_pi(100)
    print("100个点近似的圆周率：", pi)

    pi = approxiate_pi(10000)
    print("10000个点近似的圆周率：", pi)

    pi = approxiate_pi(1000000)
    print("1000000个点近似的圆周率：", pi)

输出：100个点近似的圆周率： 3.08
10000个点近似的圆周率： 3.1352
1000000个点近似的圆周率： 3.141

例二、计算阴影部分面积

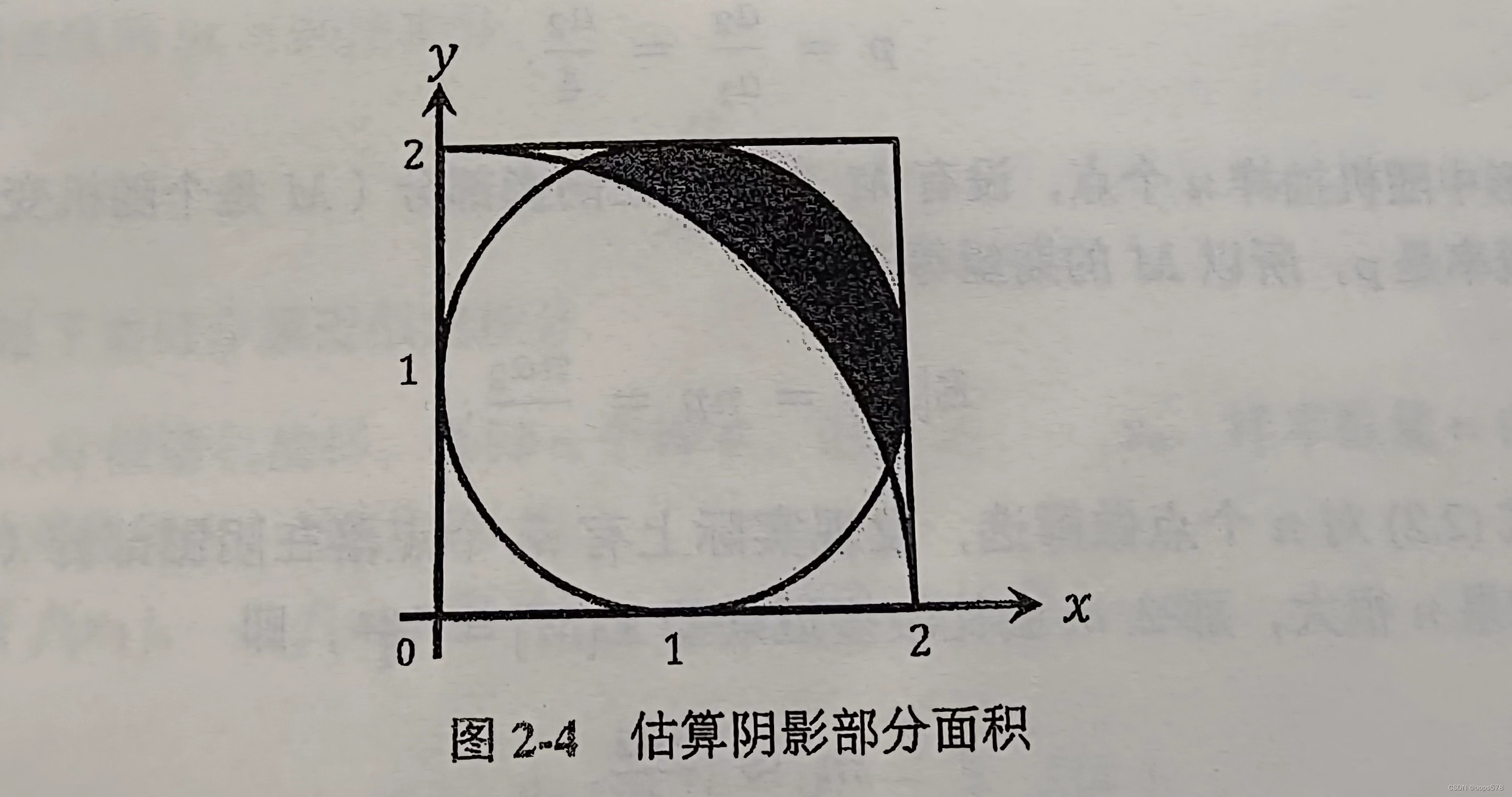
import torch
m = 0
n = 100000

for i in range(n):
    x,y = 2*torch.rand(1),2*torch.rand(1)
    if  ((x-1)**2+(y-1)**2<=1) & (x**2+y**2>4):
        m = m+1

s = 4 * m / n
print(s)

输出：0.59632

例三、计算近似期望

假设用期望计算${\int }_0^3{x}^{\frac{2}{3}}dx$

q=0
t=1
n=10000
def f(x):
    return x ** (2/3)
for i in range(n):
    a = torch.rand(1) * 3
    q = (1-1/t) * q + (1/t) * f(a)
    t = t+1
print(q)

输出：tensor([1.2374])

第二章习题2.2

# 方法1
import torch 
n = 10000
f = 0
for i in range(n):
    x = torch.normal(mean=1,std=2,size=(1,))
    f = 2*x+10*torch.sqrt(torch.abs(x))+3+f
print(f/n)

输出：tensor([17.3412])

```python
 # 方法2
import torch 
n = 10000
q=0
t=1
def f(x):
    return  2*x+10*torch.sqrt(torch.abs(x))+3
for i in range(n):
    x = torch.normal(mean=1,std=2,size=(1,))
    q = (1-1/t)*q+1/t * f(x)
    t = t+1
print(q)

输出：tensor([17.3020])