Bit Magic
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 649 Accepted Submission(s): 185
Problem Description
Yesterday, my teacher taught me about bit operators: and (&), or (|), xor (^). I generated a number table a[N], and wrote a program to calculate the matrix table b[N][N] using three kinds of bit operator. I thought my achievement would get teacher's attention.
The key function is the code showed below.
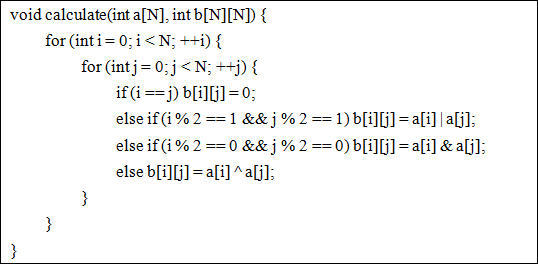
There is no doubt that my teacher raised lots of interests in my work and was surprised to my talented programming skills. After deeply thinking, he came up with another problem: if we have the matrix table b[N][N] at first, can you check whether corresponding number table a[N] exists?
The key function is the code showed below.
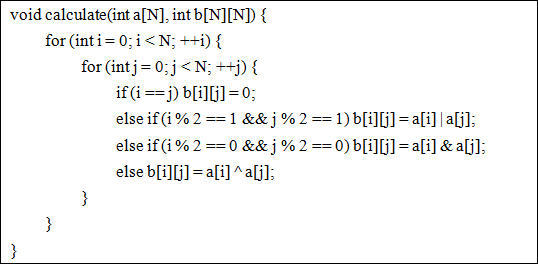
There is no doubt that my teacher raised lots of interests in my work and was surprised to my talented programming skills. After deeply thinking, he came up with another problem: if we have the matrix table b[N][N] at first, can you check whether corresponding number table a[N] exists?
Input
There are multiple test cases.
For each test case, the first line contains an integer N, indicating the size of the matrix. (1 <= N <= 500).
The next N lines, each line contains N integers, the jth integer in ith line indicating the element b[i][j] of matrix. (0 <= b[i][j] <= 2 31 - 1)
For each test case, the first line contains an integer N, indicating the size of the matrix. (1 <= N <= 500).
The next N lines, each line contains N integers, the jth integer in ith line indicating the element b[i][j] of matrix. (0 <= b[i][j] <= 2 31 - 1)
Output
For each test case, output "YES" if corresponding number table a[N] exists; otherwise output "NO".
Sample Input
2 0 4 4 0 3 0 1 24 1 0 86 24 86 0
Sample Output
YES NO
Source
这是12年长春现场赛的B,记忆非常深刻,当年还是太年轻了,没学2SAT竟然就去长春了。。。
这是一道明显的2SAT,由于位操作每一位是单独作用的,所以可以将31位的整数拆成31位,每一位跑一次2SAT判断是否合法,具体建图和这题是一样的,非常经典的建图。
不过这题还是跪了几个小时,检查了半天,原来是一个优先级搞错了。。。。
详情请见代码:
#include <iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;
const int N = 505;
const int M = 1000005;
int table[N][N];
int head[N<<1];
int scc[N<<1];
int vis[N<<1];
int stack1[N<<1];
int stack2[N<<1];
struct edge
{
int to,next;
}g[M];
int n,num;
bool flag;
void init()
{
memset(head,-1,sizeof(head));
memset(vis,0,sizeof(vis));
memset(scc,0,sizeof(scc));
flag = true;
stack1[0] = stack2[0] = num = 0;
}
void build(int s,int e)
{
g[num].to = e;
g[num].next = head[s];
head[s] = num ++;
}
void dfs(int cur,int &sig,int &cnt)
{
if(!flag)
return;
vis[cur] = ++sig;
stack1[++stack1[0]] = cur;
stack2[++stack2[0]] = cur;
for(int i = head[cur];i != -1;i = g[i].next)
{
if(!vis[g[i].to])
dfs(g[i].to,sig,cnt);
else
{
if(!scc[g[i].to])
{
while(vis[stack2[stack2[0]]] > vis[g[i].to])
stack2[0] --;
}
}
}
if(stack2[stack2[0]] == cur)
{
stack2[0] --;
cnt ++;
do
{
scc[stack1[stack1[0]]] = cnt;
int tmp = stack1[stack1[0]];
if((tmp >= n && scc[tmp - n] == cnt) || (tmp < n && scc[tmp + n] == cnt))
{
flag = false;
return;
}
}while(stack1[stack1[0] --] != cur);
}
}
void Gabow()
{
int i,sig,cnt;
sig = cnt = 0;
for(i = 0;i < n + n && flag;i ++)
if(!vis[i])
dfs(i,sig,cnt);
}
int main()
{
int i,j,k;
while(scanf("%d",&n) != EOF)
{
for(i = 0;i < n;i ++)
for(j = 0;j < n;j ++)
scanf("%d",&table[i][j]);
flag = true;
for(i = 0;i < n;i ++)/*zoj要这一段才能过*/
{
if(table[i][i])
flag = false;
}
if(flag == false)
{
printf("NO\n");
continue;
}
for(k = 0;k < 32;k ++)
{
init();
for(i = 0;i < n;i ++)
{
for(j = 0;j < n;j ++)
{
if(i == j)
continue;
else
{
int ti = table[i][j] & (1<<k);
if((i&1) && (j&1))//or
{
if(ti)
{
build(i,j + n);
build(j,i + n);
}
else
{
build(i + n,i);
build(j + n,j);
}
}
else
{
if((i&1) == 0 && (j&1) == 0)//and !!!!!!!!!!
{//==的优先级高于&!!!!!!!!!!!!!!
if(ti)
{
build(i,i + n);
build(j,j + n);
}
else
{
build(i + n,j);
build(j + n,i);
}
}
else//xor
{
if(ti)
{
build(i,j + n);
build(i + n,j);
build(j,i + n);
build(j + n,i);
}
else
{
build(i,j);
build(j,i);
build(i + n,j + n);
build(j + n,i + n);
}
}
}
}
}
}
Gabow();
if(flag == false)
break;
}
if(flag)
printf("YES\n");
else
printf("NO\n");
}
return 0;
}
//1234MS 7156K


























 4929
4929

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








